人教版七年级数学上册导学案:4.3.1 角(含答案)
文档属性
| 名称 | 人教版七年级数学上册导学案:4.3.1 角(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 780.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览

文档简介
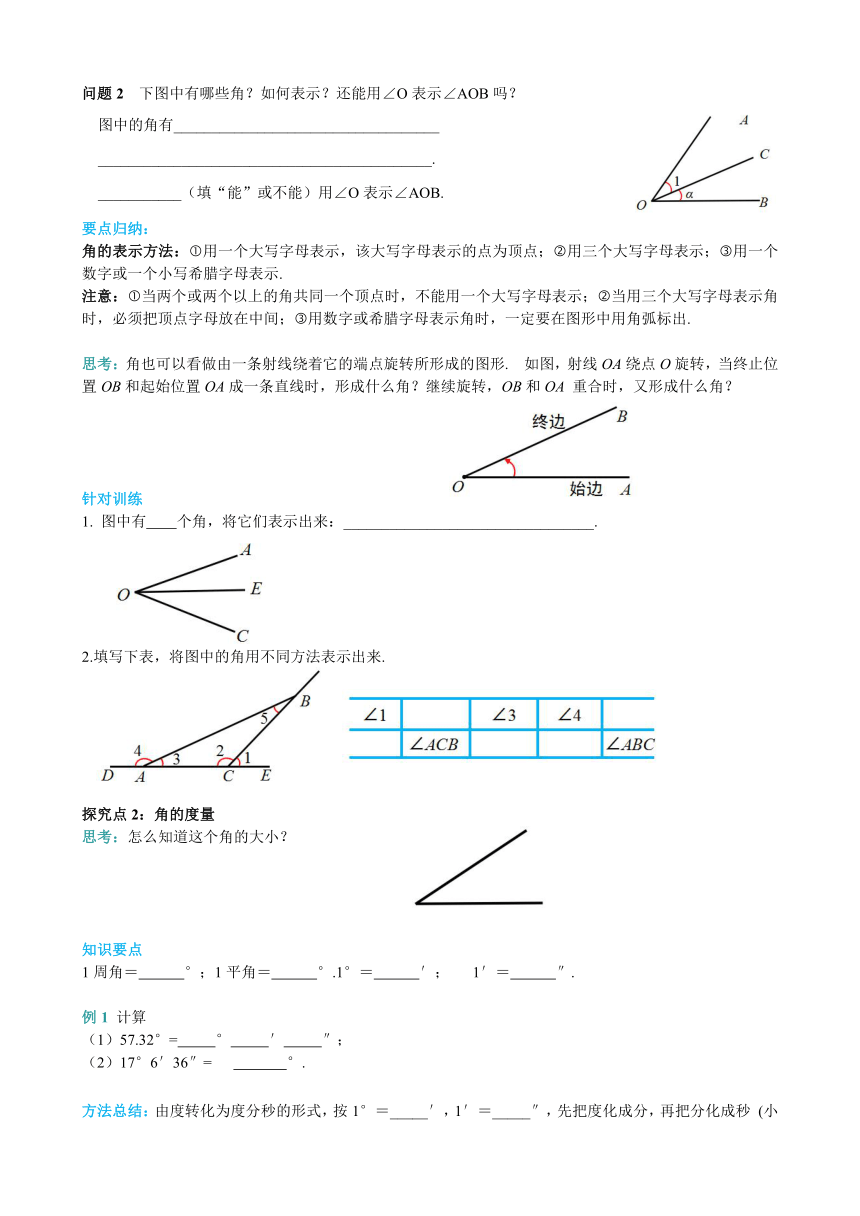
4.3.1
角
学习目标:1.
理解角的两种定义和相关概念,掌握角的表示方法.
2.
会正确使用量角器测量角的大小.
3.
认识角的单位,会进行度、分、秒之间的换算.
重点:理解角的两种定义,掌握角的表示方法,认识角的单位.
难点:会进行度、分、秒之间的换算.
【自主学习】
一、知识链接
1.
回忆小学所学的知识,说一说什么是角?
2.
直角、平角、周角各是多少度?
新知预学
观察角的图象,你能归纳出角的特点吗?尝试去描述一下角是由什么组成的图形?
要点归纳:有公共端点的两条_______组成的图形,叫做角.这个公共端点叫做角的__________,两条___________叫做角的两条边.
三、自学自测
判断下列哪些图形是角
我的疑惑
______________________________________________________________________________________________________________________________________________________
【课堂探究】
要点探究
探究点1:角的概念及表示方法
问题1
有哪些方式可以表示如图所示的角?
问题2
下图中有哪些角?如何表示?还能用∠O表示∠AOB吗?
要点归纳:
角的表示方法:用一个大写字母表示,该大写字母表示的点为顶点;用三个大写字母表示;用一个数字或一个小写希腊字母表示.
注意:当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示;当用三个大写字母表示角时,必须把顶点字母放在中间;用数字或希腊字母表示角时,一定要在图形中用角弧标出.
思考:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
如图,射线OA绕点O旋转,当终止位置OB和起始位置OA成一条直线时,形成什么角?继续旋转,OB和OA
重合时,又形成什么角?
针对训练
1.
图中有 个角,将它们表示出来:_________________________________.
2.填写下表,将图中的角用不同方法表示出来.
探究点2:角的度量
思考:怎么知道这个角的大小?
知识要点
1周角= °;1平角= °.1°= ′;
1′= ″.
例1
计算
(1)57.32°=
°
′
″;
(2)17°6′36″=
°.
方法总结:由度转化为度分秒的形式,按1°=_____′,1′=_____″,先把度化成分,再把分化成秒
(小数化整数);由度分秒转化为度的形式,按1″=_____′,1′=_____°先把秒化成分,再把分化成度
(整数化小数).
例2
如图,时钟显示为10:10时,时针与分针所夹角度是
(
)
A.90°
B.100°
C.105°
D.115°
针对训练
1.计算:
(1)5°= ′=
″;(2)38.15°= ° ′;
(3)36″= ′= °;(4)38°15′= °.
时钟显示为9:30时,时针与分针所夹角度是_________°.
二、课堂小结
【当堂检测】
1.
下列语句正确的是
(
)
A.
两条直线相交,组成的图形叫做角
B.
两条有公共端点的线段组成的图形叫做角
C.
两条有公共点的射线组成的图形叫做角
D.
从同一点引出的两条射线组成的图形叫做角
2.
下列说法不正确的是
(
)
A.
∠AOB的顶点是O
B.
射线BO,AO分别是∠AOB的两条边
C.
∠AOB的边是两条射线
D.
∠AOB与∠BOA表示同一个角
3.
甲、乙、丙、丁四名学生在判断钟表的分针和时针互相垂直的时刻时,每人说了两个时刻,说法都对的是( )
A.甲:“3时整和3时30分”
B.乙说“6时15分和6时45分”
C.丙说“9时整和12时15分”
D.丁说:“3时整和9时整”
4.
判断
(1)
直线是一个平角
(
)
(2)
如图①,点P不在∠AOB的内部
(
)
(3)
如图②,∠ABC与∠DBE是同一个角
(
)
5.
如图所示:
(1)
图中共有多少个角?请写出能用一个字母表示的角;
(2)
把图中所有的角都表示出来.
6.
38°15′和38.15°相等吗?如不相等,请说明它们的大小关系.
7.
(1)
如图∠AOB内部画1条射线,问图中一共有多少个角?如果是画2条呢?3条呢?
(2)
∠AOB内部画99条射线,问图中一共有多少个角?如果是
(n-1)
条呢?
参考答案
自主学习
一、知识链接
1.一条射线绕着它的端点旋转而形成的图形叫做角.
2.直角为90°,平角为180°,周角为360°.
二、新知预习
角是由两条射线组成,且有公共端点.
【要点归纳】射线
顶点
射线
三、自学自测
√
×
√
√
合作探究
一、要点探究
探究点1:
问题1
1.O
2.AOB
BOA
3.α
问题2
∠AOC(或∠1)、∠BOC(或∠α)、∠AOB
不能
思考
平角;周角.
【针对训练】
1.3
∠AOE,∠COE,∠AOC
2.
∠2
∠5
∠BCE
∠BAC
∠BAD
探究点2:
思考
可以用量角器测量.
知识要点
360
180
60
60
例1
(1)57
19
12
(2)17.11
方法总结
60
60
例2
D
【针对训练】
1.(1)300
18000
(2)38
9
(3)0.6
0.01
(4)38.25
2.105
当堂检测
1.D
2.B
3.D
4.(1)×
(2)×
(3)√
5.解:(1)8个;∠A,∠O.
(2)∠A,∠O,∠1,∠2,∠3,∠4,∠ABC,∠ACB.
6.解:∵
38°15′
=
38.25°,∴
38°15′
>
38.15°.
7.解:(1)3个,6个,10个.
(2)
5050个,(1+2+3+…+n)个.
角
学习目标:1.
理解角的两种定义和相关概念,掌握角的表示方法.
2.
会正确使用量角器测量角的大小.
3.
认识角的单位,会进行度、分、秒之间的换算.
重点:理解角的两种定义,掌握角的表示方法,认识角的单位.
难点:会进行度、分、秒之间的换算.
【自主学习】
一、知识链接
1.
回忆小学所学的知识,说一说什么是角?
2.
直角、平角、周角各是多少度?
新知预学
观察角的图象,你能归纳出角的特点吗?尝试去描述一下角是由什么组成的图形?
要点归纳:有公共端点的两条_______组成的图形,叫做角.这个公共端点叫做角的__________,两条___________叫做角的两条边.
三、自学自测
判断下列哪些图形是角
我的疑惑
______________________________________________________________________________________________________________________________________________________
【课堂探究】
要点探究
探究点1:角的概念及表示方法
问题1
有哪些方式可以表示如图所示的角?
问题2
下图中有哪些角?如何表示?还能用∠O表示∠AOB吗?
要点归纳:
角的表示方法:用一个大写字母表示,该大写字母表示的点为顶点;用三个大写字母表示;用一个数字或一个小写希腊字母表示.
注意:当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示;当用三个大写字母表示角时,必须把顶点字母放在中间;用数字或希腊字母表示角时,一定要在图形中用角弧标出.
思考:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
如图,射线OA绕点O旋转,当终止位置OB和起始位置OA成一条直线时,形成什么角?继续旋转,OB和OA
重合时,又形成什么角?
针对训练
1.
图中有 个角,将它们表示出来:_________________________________.
2.填写下表,将图中的角用不同方法表示出来.
探究点2:角的度量
思考:怎么知道这个角的大小?
知识要点
1周角= °;1平角= °.1°= ′;
1′= ″.
例1
计算
(1)57.32°=
°
′
″;
(2)17°6′36″=
°.
方法总结:由度转化为度分秒的形式,按1°=_____′,1′=_____″,先把度化成分,再把分化成秒
(小数化整数);由度分秒转化为度的形式,按1″=_____′,1′=_____°先把秒化成分,再把分化成度
(整数化小数).
例2
如图,时钟显示为10:10时,时针与分针所夹角度是
(
)
A.90°
B.100°
C.105°
D.115°
针对训练
1.计算:
(1)5°= ′=
″;(2)38.15°= ° ′;
(3)36″= ′= °;(4)38°15′= °.
时钟显示为9:30时,时针与分针所夹角度是_________°.
二、课堂小结
【当堂检测】
1.
下列语句正确的是
(
)
A.
两条直线相交,组成的图形叫做角
B.
两条有公共端点的线段组成的图形叫做角
C.
两条有公共点的射线组成的图形叫做角
D.
从同一点引出的两条射线组成的图形叫做角
2.
下列说法不正确的是
(
)
A.
∠AOB的顶点是O
B.
射线BO,AO分别是∠AOB的两条边
C.
∠AOB的边是两条射线
D.
∠AOB与∠BOA表示同一个角
3.
甲、乙、丙、丁四名学生在判断钟表的分针和时针互相垂直的时刻时,每人说了两个时刻,说法都对的是( )
A.甲:“3时整和3时30分”
B.乙说“6时15分和6时45分”
C.丙说“9时整和12时15分”
D.丁说:“3时整和9时整”
4.
判断
(1)
直线是一个平角
(
)
(2)
如图①,点P不在∠AOB的内部
(
)
(3)
如图②,∠ABC与∠DBE是同一个角
(
)
5.
如图所示:
(1)
图中共有多少个角?请写出能用一个字母表示的角;
(2)
把图中所有的角都表示出来.
6.
38°15′和38.15°相等吗?如不相等,请说明它们的大小关系.
7.
(1)
如图∠AOB内部画1条射线,问图中一共有多少个角?如果是画2条呢?3条呢?
(2)
∠AOB内部画99条射线,问图中一共有多少个角?如果是
(n-1)
条呢?
参考答案
自主学习
一、知识链接
1.一条射线绕着它的端点旋转而形成的图形叫做角.
2.直角为90°,平角为180°,周角为360°.
二、新知预习
角是由两条射线组成,且有公共端点.
【要点归纳】射线
顶点
射线
三、自学自测
√
×
√
√
合作探究
一、要点探究
探究点1:
问题1
1.O
2.AOB
BOA
3.α
问题2
∠AOC(或∠1)、∠BOC(或∠α)、∠AOB
不能
思考
平角;周角.
【针对训练】
1.3
∠AOE,∠COE,∠AOC
2.
∠2
∠5
∠BCE
∠BAC
∠BAD
探究点2:
思考
可以用量角器测量.
知识要点
360
180
60
60
例1
(1)57
19
12
(2)17.11
方法总结
60
60
例2
D
【针对训练】
1.(1)300
18000
(2)38
9
(3)0.6
0.01
(4)38.25
2.105
当堂检测
1.D
2.B
3.D
4.(1)×
(2)×
(3)√
5.解:(1)8个;∠A,∠O.
(2)∠A,∠O,∠1,∠2,∠3,∠4,∠ABC,∠ACB.
6.解:∵
38°15′
=
38.25°,∴
38°15′
>
38.15°.
7.解:(1)3个,6个,10个.
(2)
5050个,(1+2+3+…+n)个.
