5.4 二次函数与一元二次方程 同步测试题(含答案)
文档属性
| 名称 | 5.4 二次函数与一元二次方程 同步测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 10:56:57 | ||
图片预览

文档简介
5.4
二次函数与一元二次方程
同步测试题
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
二次函数=的图象与轴的交点坐标是(
)
A.
B.
C.
D.或
?
2.
已知抛物线,与轴的一个交点为,则代数式的值为(
)
A.
B.
C.
D.
?
3.
下列关于二次函数=的图象与轴交点的判断,正确的是(
)
A.没有交点
B.只有一个交点,且它位于轴右侧
C.有两个交点,且它们均位于轴左侧
D.有两个交点,且它们均位于轴右侧
?
4.
已知二次函数的图象如图所示,则一元二次方程的近似解为(
)
A.,
B.,
C.,
D.,
?5.
对二次函数,当时,自变量的取值范围是(
)
A.
B.
C.
D.或
?
6.
已知二次函数的图象与正比例函数的图象交于点,与轴交于点,若,则的取值范围是(
)
A.
B.
C.
D.或
?
7.
下列表格是二次函数的自变量与函数值的对应值,判断方程(,,,为常数)的一个解的范围是(?
?
?
?
)
?
A.
B.
C.
D.
?
8.
若抛物线与轴的交点坐标为,则代数式的值为(
)
A.
B.
C.
D.
?
9.
已知二次函数图象的顶点的横坐标是,图象交轴于点和点,且,那么的长是?
?
?
?
A.
B.
C.
D.
?
10.
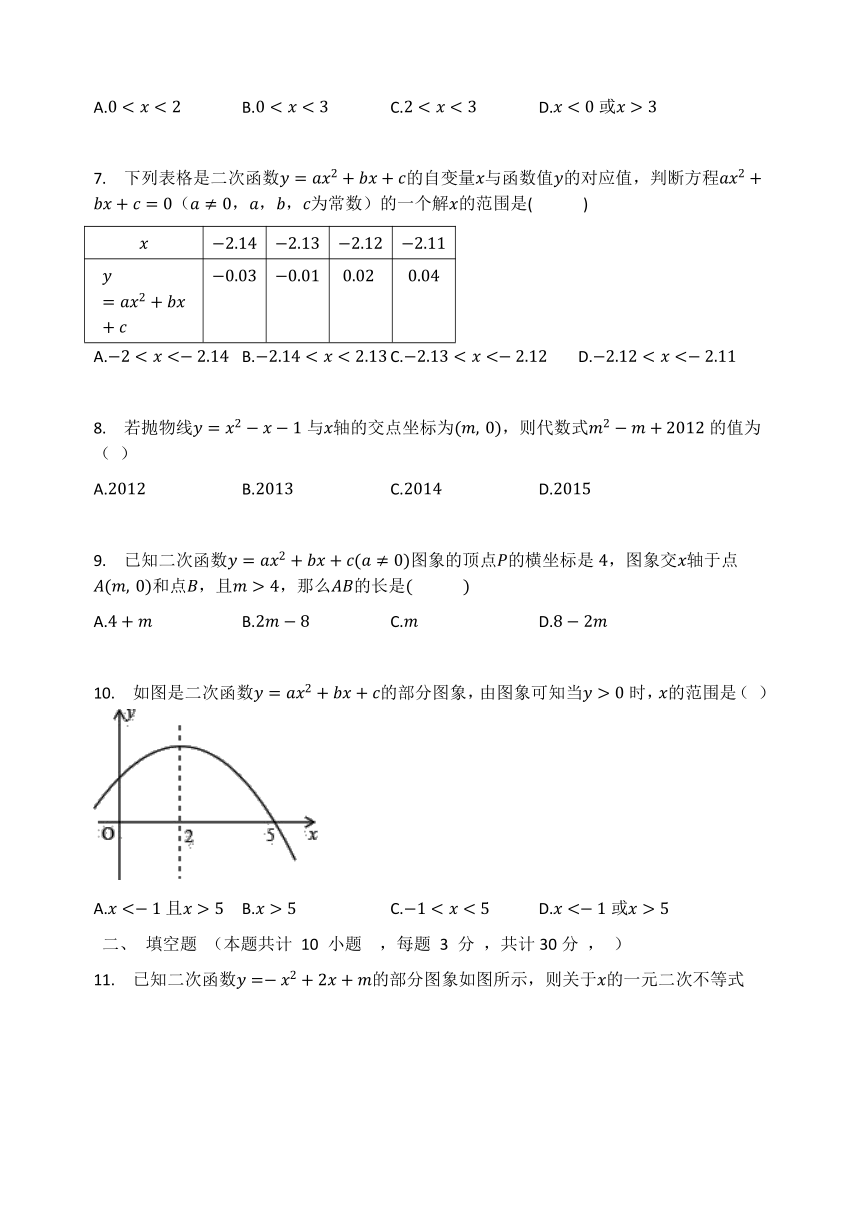
如图是二次函数的部分图象,由图象可知当时,的范围是(
)
A.且
B.
C.
D.或
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
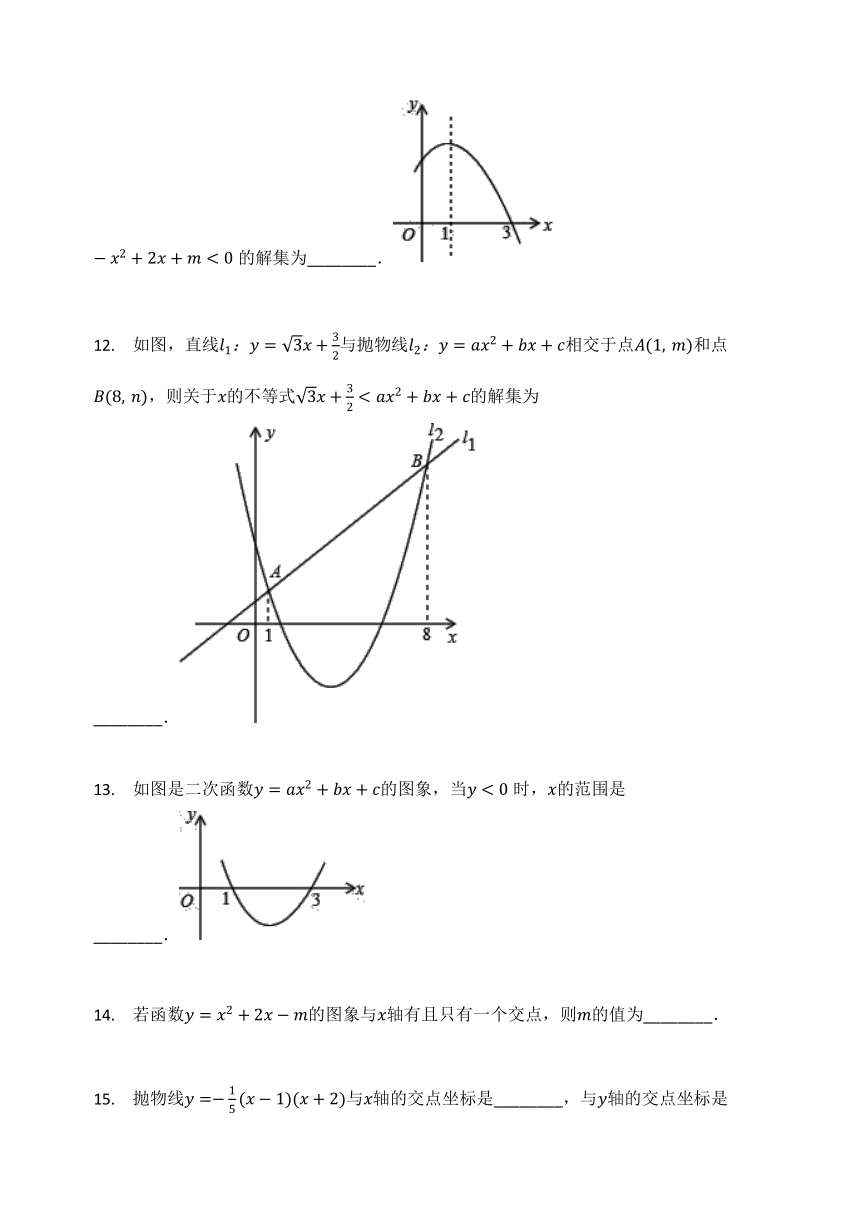
已知二次函数的部分图象如图所示,则关于的一元二次不等式的解集为________.
?
12.
如图,直线与抛物线相交于点和点,则关于的不等式的解集为________.
?
13.
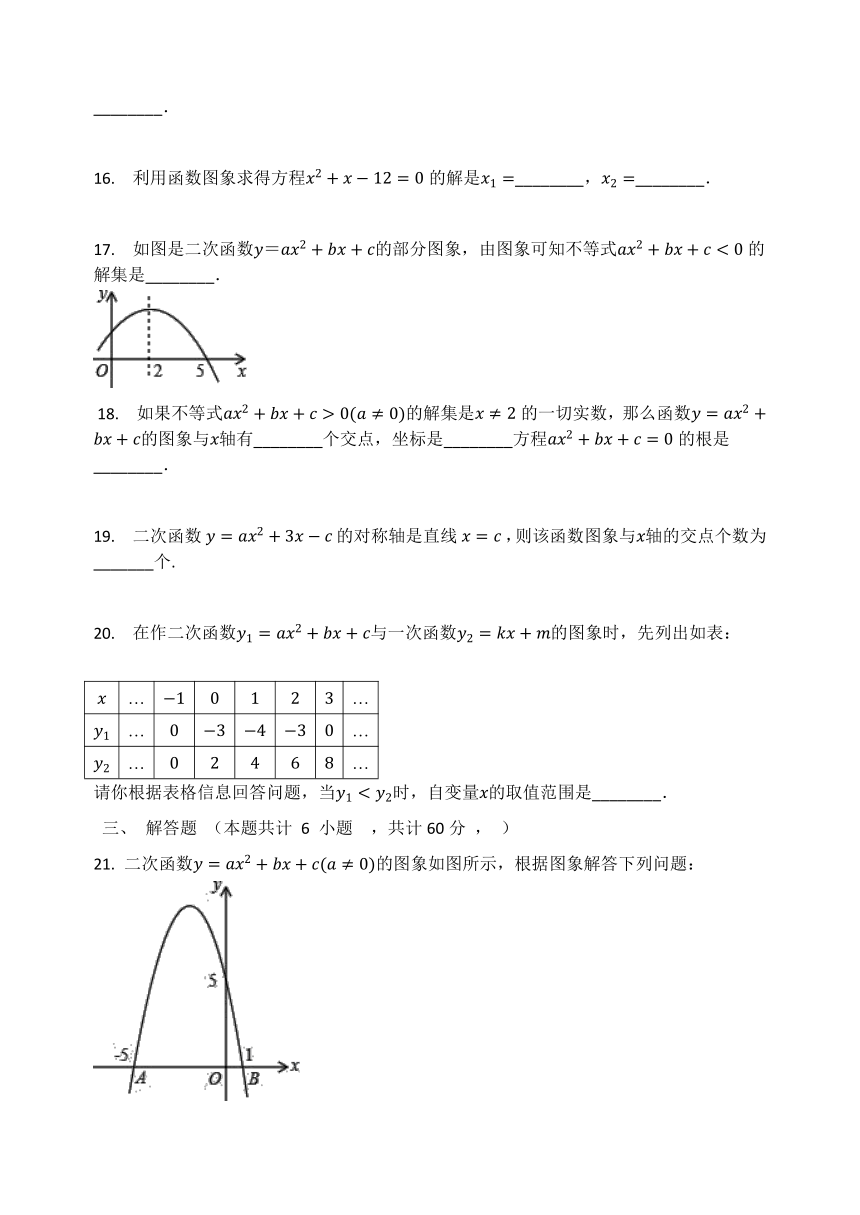
如图是二次函数的图象,当时,的范围是________.
?
14.
若函数的图象与轴有且只有一个交点,则的值为________.
?
15.
抛物线与轴的交点坐标是________,与轴的交点坐标是________.
?
16.
利用函数图象求得方程的解是________,________.
?
17.
如图是二次函数=的部分图象,由图象可知不等式的解集是________.
?18.
如果不等式的解集是的一切实数,那么函数的图象与轴有________个交点,坐标是________方程的根是________.
?
19.
二次函数??的对称轴是直线??,则该函数图象与轴的交点个数为_______个.
?
20.
在作二次函数与一次函数的图象时,先列出如表:
…
…
…
…
…
…
请你根据表格信息回答问题,当时,自变量的取值范围是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
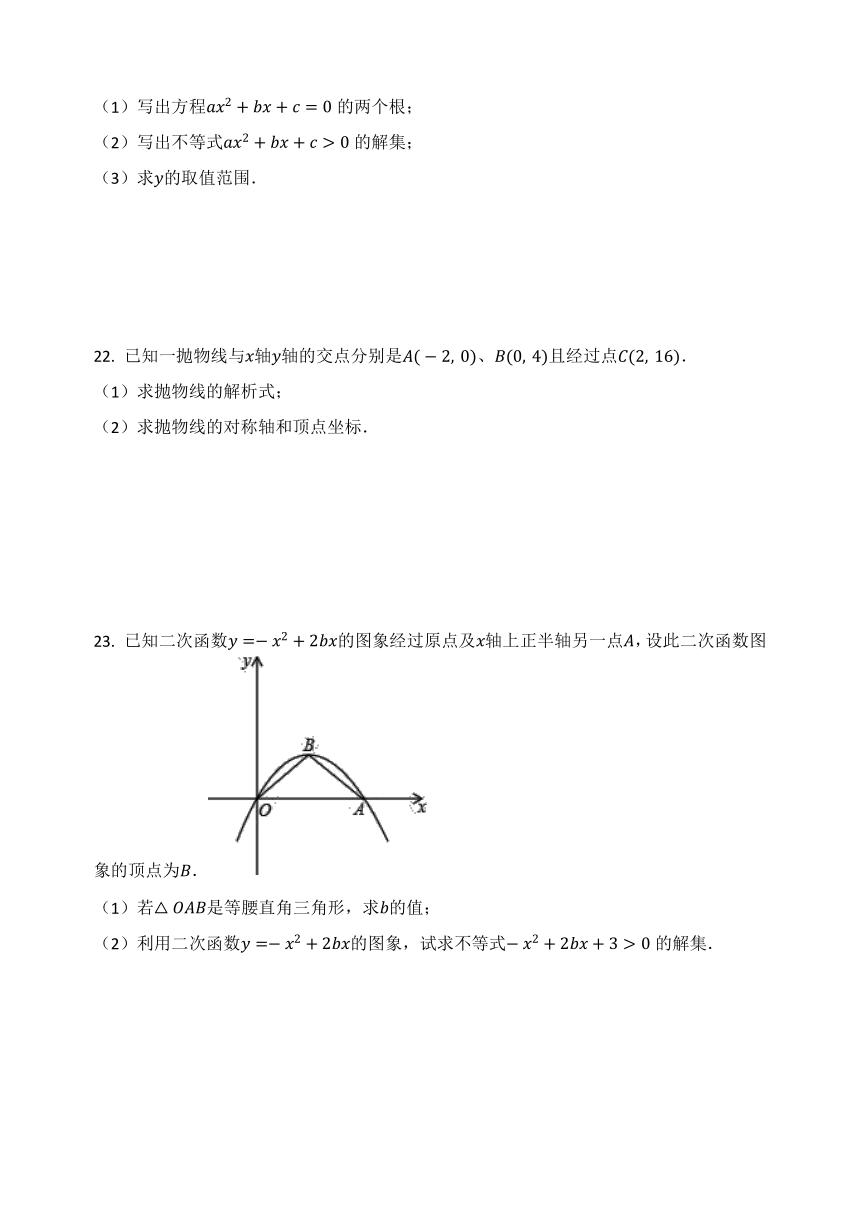
二次函数的图象如图所示,根据图象解答下列问题:
(1)写出方程的两个根;
(2)写出不等式的解集;
(3)求的取值范围.
?
22.
已知一抛物线与轴轴的交点分别是、且经过点.
(1)求抛物线的解析式;?????????
(2)求抛物线的对称轴和顶点坐标.
?
23.
已知二次函数的图象经过原点及轴上正半轴另一点,设此二次函数图象的顶点为.
(1)若是等腰直角三角形,求的值;
(2)利用二次函数的图象,试求不等式的解集.
?
24.
如图,抛物线与轴交于、两点,与轴交于点,其顶点在直线上.
(1)求的值;
(2)求、两点的坐标.
?
25.
已知二次函数.
(1)如果该二次函数的图象与轴有两个交点,求的取值范围;
(2)如果该二次函数的图象与轴交于、两点,与轴交于点,且点的坐标为,求它的表达式和点的坐标;
(3)如果一次函数的图象经过点、,请根据图象直接写出时,的取值范围.
?
26.
阅读材料,解答问题.
例.用图象法解一元二次不等式:.
解:设,则是的二次函数.∵
,∴
抛物线开口向上.
又∵
当时,,解得,.∴
由此得抛物线的大致图象如图所示.观察函数图象可知:当或时,.∴
的解集是:或.
(1)观察图象,直接写出一元二次不等式:的解集是________;
(2)仿照上例,用图象法解一元二次不等式:.(画出大致图象).
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
D
【解答】
令=,代入函数解析式得,=,
解得=,=,
∴
二次函数图象与轴交点坐标为或,
2.
【答案】
B
【解答】
解:∵
抛物线,与轴的一个交点为,
∴
,
∴
,
∴
,
故选.
3.
【答案】
D
【解答】
当=时,=,
∵
∴
==,
=有两个根,函数与有两个交点,
,
4.
【答案】
B
【解答】
解:依题意得二次函数的部分图象的对称轴为,
而对称轴右侧图象与轴交点与原点的距离,约为,
∴
;
又∵
对称轴为,
则,
∴
.
故,.
故选:.
5.
【答案】
A
【解答】
解:∵
二次函数中,,
∴
抛物线开口向上.
∵
令,则或,
∴
抛物线与轴的交点坐标为,,
∴
当时,.
故选.
6.
【答案】
B
【解答】
解:如图所示:若,则二次函数图象在一次函数图象的下面,
此时的取值范围是:.
故选:.
7.
【答案】
C
【解答】
解:函数的图象与轴的交点就是方程的根,
函数的图象与轴的交点的纵坐标为;
由表中数据可知:在与之间,
∴
对应的的值在与之间,即.
故选.
8.
【答案】
B
【解答】
解:∵
抛物线与轴的交点坐标为,
∴
为方程的解,
∴
,即,
∴
.
故选.
9.
【答案】
B
【解答】
解:因为二次函数图象的顶点的横坐标是,
所以抛物线对称轴所在直线为,交轴于点,
所以,两点关于对称轴对称,
因为点,且,即,
所以.
故选.?
10.
【答案】
C
【解答】
解:由图可知,二次函数图象与轴的另一交点坐标为,
所以,当时,的范围是.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
或
【解答】
解:由图可知,对称轴为直线,
所以,二次函数图象与轴的另一个交点坐标为,
所以,的解集为或.
故答案为:或.
12.
【答案】
或
【解答】
解:∵
抛物线与直线相交于和两点,
∴
关于的不等式的解集是或.
故答案为:或.
13.
【答案】
【解答】
解:由图可知,时,.
故答案为:.
14.
【答案】
【解答】
解:函数的图象与轴有且只有一个交点,
,
解得:.
故答案为:.
15.
【答案】
,,
【解答】
解:∵
抛物线,
∴
轴的交点坐标是:,,
令,得,
∴
轴的交点坐标是:.
16.
【答案】
,
【解答】
解:∵
方程的解就是函数的图象与轴的交点的横坐标,
而的图象如图所示:
∴
的图象与轴的交点坐标为、,
∴
方程的解是,.
17.
【答案】
或
【解答】
由图可知,对称轴为直线=,与轴的一个交点坐标为,
∴
函数图象与轴的另一交点坐标为,
∴
的解集是或.
18.
【答案】
,,
【解答】
解:∵
不等式的解集是的一切实数,
∴
函数的图象开口向上,且与轴有一个交点,
∴
函数与轴的交点坐标为,
∴
方程的根是.
故答案为:,,.
19.
【答案】
【解答】
解:二次函数
的对称轴是直线
,
∴
,
∴
,
∴
一元二次方程
的根的判别式
,
∴
一元二次方程
有两个不等的实数根,
∴
该函数图象与轴的交点个数为个.
故答案为:.
20.
【答案】
【解答】
解:∵
由题意得,,
解得,
∴
二次函数的解析式为,
∵
一次函数的图象过点,,
∴
,
解得,
∴
一次函数的解析式为,
如图所示,当时,二次函数的值小于一次函数的值.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:(1)如图所示:方程的两个根为:或;
(2)如图所示:不等式的解集为:;
(3)∵
抛物线与坐标轴分别交于点,,,
设抛物线解析式为:,
∵
抛物线过点,
∴
,
解得:,
∴
抛物线解析式为:,
∵
,
∴
当时,
,
∴
的取值范围为:.
【解答】
解:(1)如图所示:方程的两个根为:或;
(2)如图所示:不等式的解集为:;
(3)∵
抛物线与坐标轴分别交于点,,,
设抛物线解析式为:,
∵
抛物线过点,
∴
,
解得:,
∴
抛物线解析式为:,
∵
,
∴
当时,
,
∴
的取值范围为:.
22.
【答案】
解:(1)设抛物线的解析式为,
∵
与轴的交点是,
∴
,
∵
经过,,
∴
,
解得:,
∴
抛物线的解析式为;?????
(2)抛物线的对称轴是,
,
顶点坐标是.
【解答】
解:(1)设抛物线的解析式为,
∵
与轴的交点是,
∴
,
∵
经过,,
∴
,
解得:,
∴
抛物线的解析式为;?????
(2)抛物线的对称轴是,
,
顶点坐标是.
23.
【答案】
解:(1)∵
是等腰直角三角形,
∴
设点横坐标为:,则,
故点纵坐标为;,
则,,则,
故整理得:,
解得:(不合题意舍去),,
故;
(2)由(1)得:,
则是向上平移个单位得到的,
故时,
解得:,,
如图所示:不等式的解集为:.
【解答】
解:(1)∵
是等腰直角三角形,
∴
设点横坐标为:,则,
故点纵坐标为;,
则,,则,
故整理得:,
解得:(不合题意舍去),,
故;
(2)由(1)得:,
则是向上平移个单位得到的,
故时,
解得:,,
如图所示:不等式的解集为:.
24.
【答案】
解:(1)∵
抛物线的顶点的横坐标为:,其顶点在直线上,
∴
抛物线的顶点的纵坐标为:,
∴
,
∴
;
(2)∵
,
∴
抛物线的解析式为:,
由得:,,
∴
、两点的坐标是,.
【解答】
解:(1)∵
抛物线的顶点的横坐标为:,其顶点在直线上,
∴
抛物线的顶点的纵坐标为:,
∴
,
∴
;
(2)∵
,
∴
抛物线的解析式为:,
由得:,,
∴
、两点的坐标是,.
25.
【答案】
解:(1)∵
二次函数的图象与轴有两个交点,
∴
,
∴
,
解得:;
(2)∵
二次函数的图象经过点,
∴
,
解得:,
∴
它的表达式是,
∵
当时,,
∴
;
(3)由图象可知:当时,的取值范围是或.
【解答】
解:(1)∵
二次函数的图象与轴有两个交点,
∴
,
∴
,
解得:;
(2)∵
二次函数的图象经过点,
∴
,
解得:,
∴
它的表达式是,
∵
当时,,
∴
;
(3)由图象可知:当时,的取值范围是或.
26.
【答案】
解:(1)观察图象,可得一元二次不等式的解集是:
(2)设,则是的二次函数.
∵
,∴
抛物线开口向上.
又∵
当时,,
解得,.
∴
由此得抛物线的大致图象如图所示.
观察函数图象可知:当时,.
∴
的解集是:
【解答】
解:(1)观察图象,可得一元二次不等式的解集是:
(2)设,则是的二次函数.
∵
,∴
抛物线开口向上.
又∵
当时,,
解得,.
∴
由此得抛物线的大致图象如图所示.
观察函数图象可知:当时,.
∴
的解集是:
二次函数与一元二次方程
同步测试题
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
二次函数=的图象与轴的交点坐标是(
)
A.
B.
C.
D.或
?
2.
已知抛物线,与轴的一个交点为,则代数式的值为(
)
A.
B.
C.
D.
?
3.
下列关于二次函数=的图象与轴交点的判断,正确的是(
)
A.没有交点
B.只有一个交点,且它位于轴右侧
C.有两个交点,且它们均位于轴左侧
D.有两个交点,且它们均位于轴右侧
?
4.
已知二次函数的图象如图所示,则一元二次方程的近似解为(
)
A.,
B.,
C.,
D.,
?5.
对二次函数,当时,自变量的取值范围是(
)
A.
B.
C.
D.或
?
6.
已知二次函数的图象与正比例函数的图象交于点,与轴交于点,若,则的取值范围是(
)
A.
B.
C.
D.或
?
7.
下列表格是二次函数的自变量与函数值的对应值,判断方程(,,,为常数)的一个解的范围是(?
?
?
?
)
?
A.
B.
C.
D.
?
8.
若抛物线与轴的交点坐标为,则代数式的值为(
)
A.
B.
C.
D.
?
9.
已知二次函数图象的顶点的横坐标是,图象交轴于点和点,且,那么的长是?
?
?
?
A.
B.
C.
D.
?
10.
如图是二次函数的部分图象,由图象可知当时,的范围是(
)
A.且
B.
C.
D.或
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
已知二次函数的部分图象如图所示,则关于的一元二次不等式的解集为________.
?
12.
如图,直线与抛物线相交于点和点,则关于的不等式的解集为________.
?
13.
如图是二次函数的图象,当时,的范围是________.
?
14.
若函数的图象与轴有且只有一个交点,则的值为________.
?
15.
抛物线与轴的交点坐标是________,与轴的交点坐标是________.
?
16.
利用函数图象求得方程的解是________,________.
?
17.
如图是二次函数=的部分图象,由图象可知不等式的解集是________.
?18.
如果不等式的解集是的一切实数,那么函数的图象与轴有________个交点,坐标是________方程的根是________.
?
19.
二次函数??的对称轴是直线??,则该函数图象与轴的交点个数为_______个.
?
20.
在作二次函数与一次函数的图象时,先列出如表:
…
…
…
…
…
…
请你根据表格信息回答问题,当时,自变量的取值范围是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
二次函数的图象如图所示,根据图象解答下列问题:
(1)写出方程的两个根;
(2)写出不等式的解集;
(3)求的取值范围.
?
22.
已知一抛物线与轴轴的交点分别是、且经过点.
(1)求抛物线的解析式;?????????
(2)求抛物线的对称轴和顶点坐标.
?
23.
已知二次函数的图象经过原点及轴上正半轴另一点,设此二次函数图象的顶点为.
(1)若是等腰直角三角形,求的值;
(2)利用二次函数的图象,试求不等式的解集.
?
24.
如图,抛物线与轴交于、两点,与轴交于点,其顶点在直线上.
(1)求的值;
(2)求、两点的坐标.
?
25.
已知二次函数.
(1)如果该二次函数的图象与轴有两个交点,求的取值范围;
(2)如果该二次函数的图象与轴交于、两点,与轴交于点,且点的坐标为,求它的表达式和点的坐标;
(3)如果一次函数的图象经过点、,请根据图象直接写出时,的取值范围.
?
26.
阅读材料,解答问题.
例.用图象法解一元二次不等式:.
解:设,则是的二次函数.∵
,∴
抛物线开口向上.
又∵
当时,,解得,.∴
由此得抛物线的大致图象如图所示.观察函数图象可知:当或时,.∴
的解集是:或.
(1)观察图象,直接写出一元二次不等式:的解集是________;
(2)仿照上例,用图象法解一元二次不等式:.(画出大致图象).
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
D
【解答】
令=,代入函数解析式得,=,
解得=,=,
∴
二次函数图象与轴交点坐标为或,
2.
【答案】
B
【解答】
解:∵
抛物线,与轴的一个交点为,
∴
,
∴
,
∴
,
故选.
3.
【答案】
D
【解答】
当=时,=,
∵
∴
==,
=有两个根,函数与有两个交点,
,
4.
【答案】
B
【解答】
解:依题意得二次函数的部分图象的对称轴为,
而对称轴右侧图象与轴交点与原点的距离,约为,
∴
;
又∵
对称轴为,
则,
∴
.
故,.
故选:.
5.
【答案】
A
【解答】
解:∵
二次函数中,,
∴
抛物线开口向上.
∵
令,则或,
∴
抛物线与轴的交点坐标为,,
∴
当时,.
故选.
6.
【答案】
B
【解答】
解:如图所示:若,则二次函数图象在一次函数图象的下面,
此时的取值范围是:.
故选:.
7.
【答案】
C
【解答】
解:函数的图象与轴的交点就是方程的根,
函数的图象与轴的交点的纵坐标为;
由表中数据可知:在与之间,
∴
对应的的值在与之间,即.
故选.
8.
【答案】
B
【解答】
解:∵
抛物线与轴的交点坐标为,
∴
为方程的解,
∴
,即,
∴
.
故选.
9.
【答案】
B
【解答】
解:因为二次函数图象的顶点的横坐标是,
所以抛物线对称轴所在直线为,交轴于点,
所以,两点关于对称轴对称,
因为点,且,即,
所以.
故选.?
10.
【答案】
C
【解答】
解:由图可知,二次函数图象与轴的另一交点坐标为,
所以,当时,的范围是.
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
或
【解答】
解:由图可知,对称轴为直线,
所以,二次函数图象与轴的另一个交点坐标为,
所以,的解集为或.
故答案为:或.
12.
【答案】
或
【解答】
解:∵
抛物线与直线相交于和两点,
∴
关于的不等式的解集是或.
故答案为:或.
13.
【答案】
【解答】
解:由图可知,时,.
故答案为:.
14.
【答案】
【解答】
解:函数的图象与轴有且只有一个交点,
,
解得:.
故答案为:.
15.
【答案】
,,
【解答】
解:∵
抛物线,
∴
轴的交点坐标是:,,
令,得,
∴
轴的交点坐标是:.
16.
【答案】
,
【解答】
解:∵
方程的解就是函数的图象与轴的交点的横坐标,
而的图象如图所示:
∴
的图象与轴的交点坐标为、,
∴
方程的解是,.
17.
【答案】
或
【解答】
由图可知,对称轴为直线=,与轴的一个交点坐标为,
∴
函数图象与轴的另一交点坐标为,
∴
的解集是或.
18.
【答案】
,,
【解答】
解:∵
不等式的解集是的一切实数,
∴
函数的图象开口向上,且与轴有一个交点,
∴
函数与轴的交点坐标为,
∴
方程的根是.
故答案为:,,.
19.
【答案】
【解答】
解:二次函数
的对称轴是直线
,
∴
,
∴
,
∴
一元二次方程
的根的判别式
,
∴
一元二次方程
有两个不等的实数根,
∴
该函数图象与轴的交点个数为个.
故答案为:.
20.
【答案】
【解答】
解:∵
由题意得,,
解得,
∴
二次函数的解析式为,
∵
一次函数的图象过点,,
∴
,
解得,
∴
一次函数的解析式为,
如图所示,当时,二次函数的值小于一次函数的值.
故答案为:.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:(1)如图所示:方程的两个根为:或;
(2)如图所示:不等式的解集为:;
(3)∵
抛物线与坐标轴分别交于点,,,
设抛物线解析式为:,
∵
抛物线过点,
∴
,
解得:,
∴
抛物线解析式为:,
∵
,
∴
当时,
,
∴
的取值范围为:.
【解答】
解:(1)如图所示:方程的两个根为:或;
(2)如图所示:不等式的解集为:;
(3)∵
抛物线与坐标轴分别交于点,,,
设抛物线解析式为:,
∵
抛物线过点,
∴
,
解得:,
∴
抛物线解析式为:,
∵
,
∴
当时,
,
∴
的取值范围为:.
22.
【答案】
解:(1)设抛物线的解析式为,
∵
与轴的交点是,
∴
,
∵
经过,,
∴
,
解得:,
∴
抛物线的解析式为;?????
(2)抛物线的对称轴是,
,
顶点坐标是.
【解答】
解:(1)设抛物线的解析式为,
∵
与轴的交点是,
∴
,
∵
经过,,
∴
,
解得:,
∴
抛物线的解析式为;?????
(2)抛物线的对称轴是,
,
顶点坐标是.
23.
【答案】
解:(1)∵
是等腰直角三角形,
∴
设点横坐标为:,则,
故点纵坐标为;,
则,,则,
故整理得:,
解得:(不合题意舍去),,
故;
(2)由(1)得:,
则是向上平移个单位得到的,
故时,
解得:,,
如图所示:不等式的解集为:.
【解答】
解:(1)∵
是等腰直角三角形,
∴
设点横坐标为:,则,
故点纵坐标为;,
则,,则,
故整理得:,
解得:(不合题意舍去),,
故;
(2)由(1)得:,
则是向上平移个单位得到的,
故时,
解得:,,
如图所示:不等式的解集为:.
24.
【答案】
解:(1)∵
抛物线的顶点的横坐标为:,其顶点在直线上,
∴
抛物线的顶点的纵坐标为:,
∴
,
∴
;
(2)∵
,
∴
抛物线的解析式为:,
由得:,,
∴
、两点的坐标是,.
【解答】
解:(1)∵
抛物线的顶点的横坐标为:,其顶点在直线上,
∴
抛物线的顶点的纵坐标为:,
∴
,
∴
;
(2)∵
,
∴
抛物线的解析式为:,
由得:,,
∴
、两点的坐标是,.
25.
【答案】
解:(1)∵
二次函数的图象与轴有两个交点,
∴
,
∴
,
解得:;
(2)∵
二次函数的图象经过点,
∴
,
解得:,
∴
它的表达式是,
∵
当时,,
∴
;
(3)由图象可知:当时,的取值范围是或.
【解答】
解:(1)∵
二次函数的图象与轴有两个交点,
∴
,
∴
,
解得:;
(2)∵
二次函数的图象经过点,
∴
,
解得:,
∴
它的表达式是,
∵
当时,,
∴
;
(3)由图象可知:当时,的取值范围是或.
26.
【答案】
解:(1)观察图象,可得一元二次不等式的解集是:
(2)设,则是的二次函数.
∵
,∴
抛物线开口向上.
又∵
当时,,
解得,.
∴
由此得抛物线的大致图象如图所示.
观察函数图象可知:当时,.
∴
的解集是:
【解答】
解:(1)观察图象,可得一元二次不等式的解集是:
(2)设,则是的二次函数.
∵
,∴
抛物线开口向上.
又∵
当时,,
解得,.
∴
由此得抛物线的大致图象如图所示.
观察函数图象可知:当时,.
∴
的解集是:
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
