2020-2021学年华东师大 版八年级上册数学《第13章 全等三角形》单元测试卷(Word版有答案)
文档属性
| 名称 | 2020-2021学年华东师大 版八年级上册数学《第13章 全等三角形》单元测试卷(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 137.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 08:42:59 | ||
图片预览


文档简介
2020-2021学年华东师大新版八年级上册数学《第13章
全等三角形》单元测试卷
一.选择题
1.△ABC中,∠B=50°,∠A=80°,若AB=6,则AC=( )
A.6
B.8
C.5
D.13
2.下列命题中真命题的个数是( )
①关于某直线对称的两个三角形是全等三角形;
②圆的直径是圆的对称轴;
③有两个角是60°的三角形是等边三角形;
④顶角和底角相等的等腰三角形是等边三角形.
A.1
B.2
C.3
D.4
3.如图,△AEC≌△ADB,若∠A=50°,∠ABD=38°,则图中∠AEC的度数是( )
A.88°
B.92°
C.95°
D.102°
4.在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件后能用“SAS”判定△ABC≌△A′B′C′的是( )
A.AC=A′C′
B.BC=B′C′
C.∠B=∠B′
D.∠C=∠C′
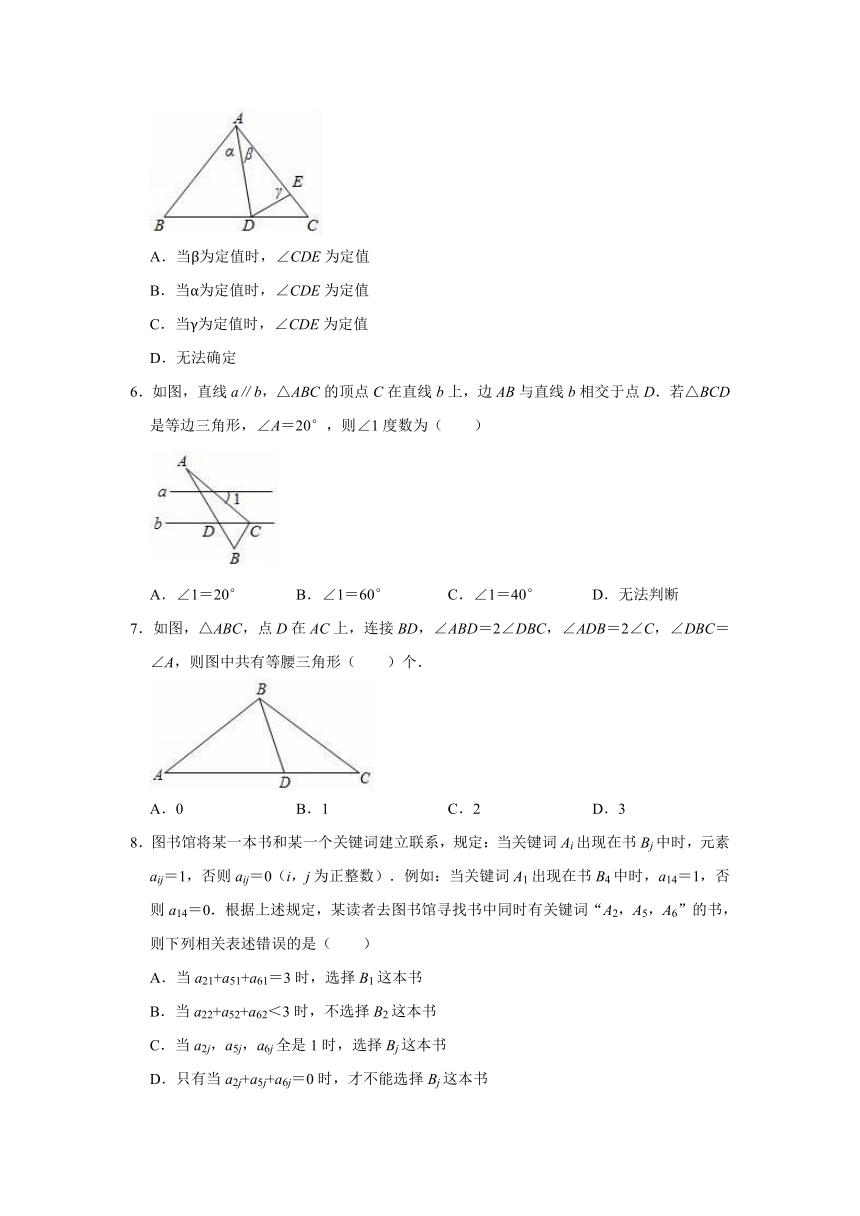
5.如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
A.当β为定值时,∠CDE为定值
B.当α为定值时,∠CDE为定值
C.当γ为定值时,∠CDE为定值
D.无法确定
6.如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1度数为( )
A.∠1=20°
B.∠1=60°
C.∠1=40°
D.无法判断
7.如图,△ABC,点D在AC上,连接BD,∠ABD=2∠DBC,∠ADB=2∠C,∠DBC=∠A,则图中共有等腰三角形( )个.
A.0
B.1
C.2
D.3
8.图书馆将某一本书和某一个关键词建立联系,规定:当关键词Ai出现在书Bj中时,元素aij=1,否则aij=0(i,j为正整数).例如:当关键词A1出现在书B4中时,a14=1,否则a14=0.根据上述规定,某读者去图书馆寻找书中同时有关键词“A2,A5,A6”的书,则下列相关表述错误的是( )
A.当a21+a51+a61=3时,选择B1这本书
B.当a22+a52+a62<3时,不选择B2这本书
C.当a2j,a5j,a6j全是1时,选择Bj这本书
D.只有当a2j+a5j+a6j=0时,才不能选择Bj这本书
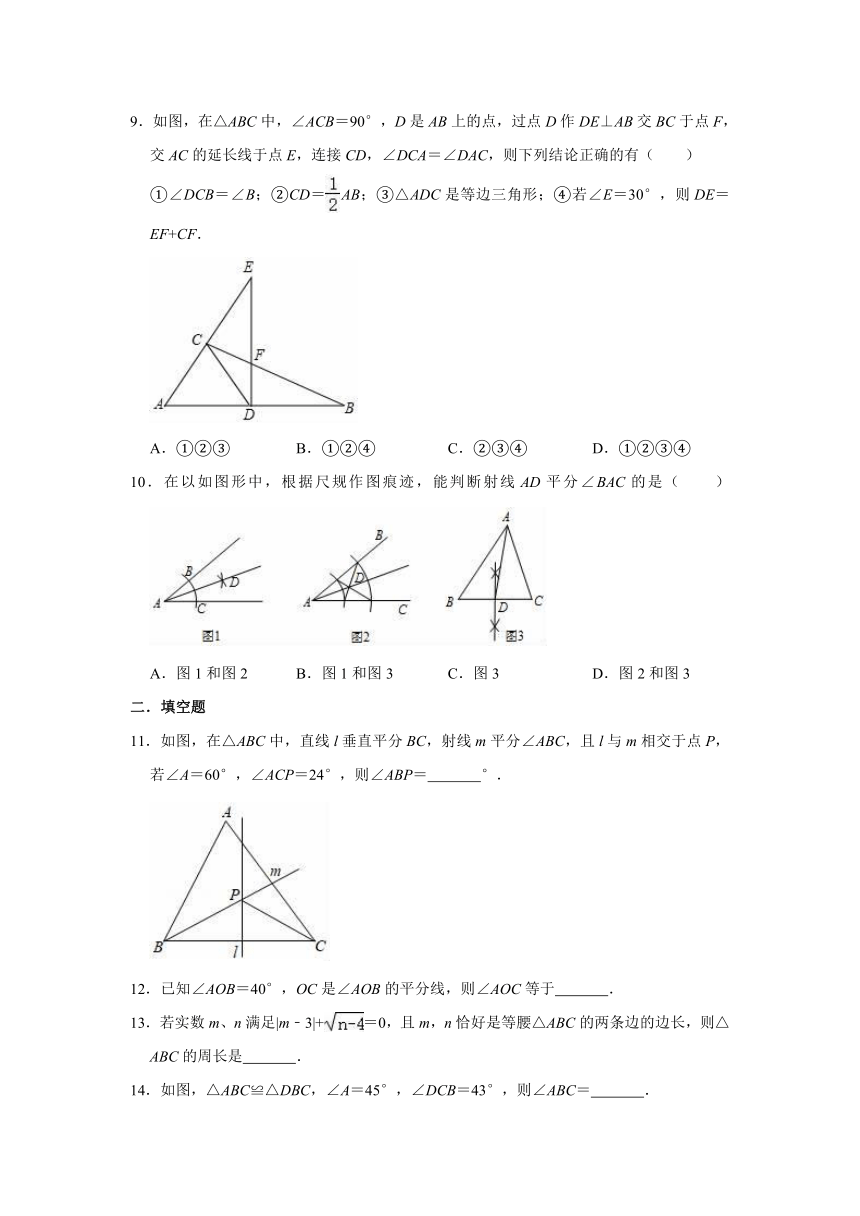
9.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③
B.①②④
C.②③④
D.①②③④
10.在以如图形中,根据尺规作图痕迹,能判断射线AD平分∠BAC的是( )
A.图1和图2
B.图1和图3
C.图3
D.图2和图3
二.填空题
11.如图,在△ABC中,直线l垂直平分BC,射线m平分∠ABC,且l与m相交于点P,若∠A=60°,∠ACP=24°,则∠ABP=
°.
12.已知∠AOB=40°,OC是∠AOB的平分线,则∠AOC等于
.
13.若实数m、n满足|m﹣3|+=0,且m,n恰好是等腰△ABC的两条边的边长,则△ABC的周长是
.
14.如图,△ABC≌△DBC,∠A=45°,∠DCB=43°,则∠ABC=
.
15.如图,AC⊥BC,AD⊥BD,垂足分别是C,D,(若要用“HL”得到Rt△ABC≌Rt△BAD,则应添加的条件是
.(写一种即可)
16.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,∠B=∠E,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是
(只需写一个,不添加辅助线).
17.若等边三角形的一边上的高为6,则它的边长为
.
18.在△ABC和△A′B′C′中,若∠A=∠A′,AB=A′B′,请你补充一个条件
,使得△ABC≌△A′B′C′.
19.甲乙丙三个人在一起聊天,每周从星期一到星期日每人连续两天说谎(包括星期日和星期一),其余五天必说真话,且任意两人不会在同一天说谎.已知周一时,乙说:“我昨天说谎了.”周二时,丙说:“太巧了,我昨天也说谎了.”则三个人都没说谎的是星期
.
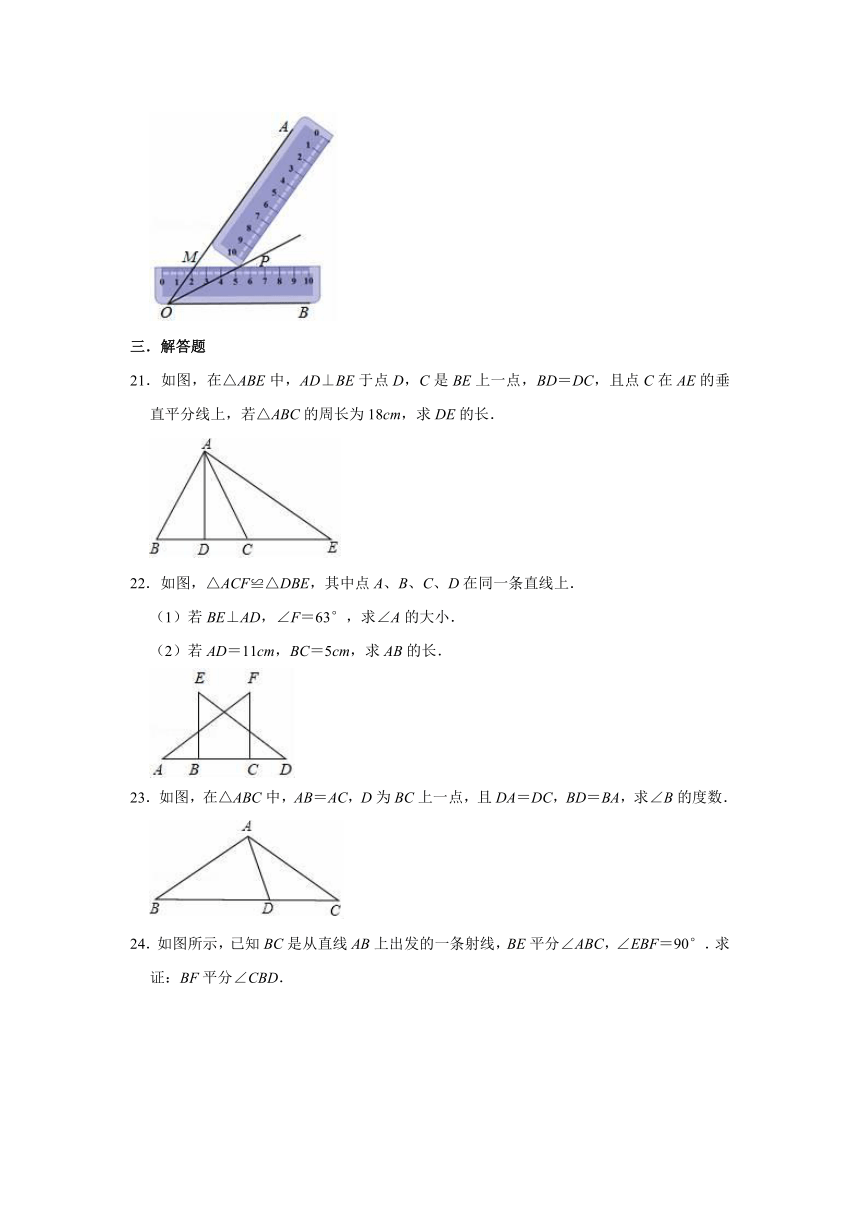
20.高兴同学在学习了全等三角形的相关知识后发现:只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB且与射线OA交于点M,另一把直尺压住射线OA且与第一把直尺交于点P,则OP平分∠AOB.若∠BOP=32°,则∠AMP=
°.
三.解答题
21.如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18cm,求DE的长.
22.如图,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小.
(2)若AD=11cm,BC=5cm,求AB的长.
23.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,求∠B的度数.
24.如图所示,已知BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.
25.世界预选赛中,中国、澳大利亚、卡塔尔和伊拉克被分在A组,进行主客场比赛.规定每场比赛胜者得三分,平局各得一分,败者不得分.比赛结束后前两名可以晋级.由于4支队伍均为强队,每支队伍至少得3分.于是甲专家预测:中国队只要得11分就能确保出线.
问:(1)这四支队的总得分之和最多有几分?
(2)甲专家的预测正确吗?为什么?
26.如图,∠ADB=∠ADC,∠B=∠C.
(1)求证:AB=AC;
(2)连接BC,求证:AD⊥BC.
27.尺规作图:如图,已知线段AB,求作线段A'B',使A'B'=AB.
参考答案与试题解析
一.选择题
1.解:∵△ABC中,∠B=50°,∠A=80°,
∴∠C=180°﹣∠A﹣∠B=180°﹣80°﹣50°=50°,
∴∠C=∠B,
∴AC=AB=6,
故选:A.
2.解:①关于某直线对称的两个三角形是全等三角形,是真命题;
②圆的直径所在的直线是圆的对称轴,本小题说法是假命题;
③有两个角是60°的三角形是等边三角形,是真命题;
④顶角和底角相等的等腰三角形是等边三角形,是真命题;
故选:C.
3.解:在△ABD中,∠A=50°,∠ABD=38°,
∴∠ADB=180°﹣∠A﹣∠ABD=92°,
∵△AEC≌△ADB,
∴∠AEC=∠ADB=92°,
故选:B.
4.解:添加AC=A'C'后能用“SAS”判定△ABC≌△A′B′C′.
在△ABC和△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS).
故选:A.
5.解:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
又∵∠ADC=∠B+∠BAD=∠B+∠α,∠AED=∠C+∠CDE,
∴∠ADE+∠CDE=∠B+∠BAD=∠B+∠α,
即∠C+∠CDE+∠CDE=∠B+∠α,
∴2∠CDE=∠α,
∴∠CDE=∠α.
即当∠α为定值时,∠CDE为定值,
故选:B.
6.解:∵△BCD是等边三角形,
∴∠BDC=60°,
∵a∥b,
∴∠2=∠BDC=60°,
由三角形的外角性质和对顶角相等可知,∠1=∠2﹣∠A=40°,
故选:C.
7.解:图中共有等腰三角形3个,理由如下:
∵∠ADB=∠C+∠DBC,∠ADB=2∠C,
∴∠DBC=∠C,
∴△BCD是等腰三角形,DB=DC,
∵∠ABD=2∠DBC,
∴∠ABD=∠ADB,
∴△ABD是等腰三角形,AB=AD,
∵∠DBC=∠A,
∴∠A=∠C,
∴△ABC是等腰三角形,AB=CB,
故选:D.
8.解:根据题意aij的值要么为1,要么为0,
A、a21+a51+a61=3,说明a21=1,a51=1,a61=1,故关键词“A2,A5,A6”同时出现在书B1中,
而读者去图书馆寻找书中同时有关键词“A2,A5,A6”的书,故A表述正确;
B、当a22+a52+a62<3时,则a22、a52、a62时必有值为0的,即关键词“A2,A5,A6”不同时具有,
从而不选择B2这本书,故B表述正确;
C、当a2j,a5j,a6j全是1时,则a2j=1,a5j=1,a6j=1,故关键词“A2,A5,A6”同时出现在书Bj中,
则选择Bj这本书,故C表述正确;
D、根据前述分析可知,只有当a2j+a5j+a6j=3时,才能选择Bj这本书,而a2j+a5j+a6j的值可能为0、1、2、3,
故D表述错误,符合题意.
故选:D.
9.解:∵在△ABC中,∠ACB=90°,DE⊥AB,
∴∠ADE=∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∵∠DCA=∠DAC,
∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD,
∵AD=CD,
∴CD=AB;故②正确;
∠DCA=∠DAC,
∴AD=CD,
但不能判定△ADC是等边三角形;故③错误;
∵若∠E=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ADC=60°,
∵∠ADE=∠ACB=90°,
∴∠EDC=∠BCD=∠B=30°,
∴CF=DF,
∴DE=EF+DF=EF+CF.故④正确.
故选:B.
10.解:在图1中,利用基本作图可判断AD平分∠BAC;
在图2中,根据作法可知:
AE=AF,AM=AN,
在△AMF和△ANE中,
,
∴△AMF≌△ANE(SAS),
∴∠AMD=∠AND,
∵∠MDE=∠NDF,
∵AE=AF,AM=AN,
∴ME=NF,
在△MDE和△NDF中,
,
∴△MDE≌△NDF(AAS),
所以D点到AM和AN的距离相等,
∴AD平分∠BAC.
在图3中,利用基本作图得到D点为BC的中点,则AD为BC边上的中线;
故选:A.
二.填空题
11.解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠CBP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
解得:∠ABP=32°,
故答案为:32.
12.解:∵OC是∠AOB的平分线,∠AOB=40°,
∴∠AOC=∠AOB=×40°=20°,
故答案为:20°.
13.解:∵|m﹣3|+=0,
∴m﹣3=0,n﹣4=0,
解得m=3,n=4,
当m=3作腰时,三边为3,3,4,符合三边关系定理,周长为:3+3+4=10,
当n=4作腰时,三边为,3,4,4,符合三边关系定理,周长为:3+4+4=11.
故答案为:10或11.
14.解:∵△ABC≌△DBC,
∴∠ACB=∠DCB=43°,
∵∠A=45°,
∴∠ABC=180°﹣∠A﹣∠ACB=92°,
故答案为:92°.
15.解:若添加AC=BD,在Rt△ABC和Rt△BAD中,,
∴Rt△ABC≌Rt△BAD(HL);
若添加BC=AD,在Rt△ABC和Rt△BAD中,,
∴Rt△ABC≌Rt△BAD(HL).
故答案为:AC=BD或BC=AD.
16.解:添加AB=ED,
∵BF=CE,
∴BF+FC=CE+FC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
故答案为:AB=ED(答案不唯一).
17.解:如图,
∵△ABC是等边三角形,且高AD=6,
∴∠ADC=90°,BD=CD=AC,
设它的边长为x,可得x2=()2+62,
解得:x=4,x=﹣4(舍去),
故答案为:4.
18.解:在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,
当添加∠B=∠B′可利用“ASA”判断△ABC≌△A′B′C′;
当添加∠C=∠C′可利用“AAS”判断△ABC≌△A′B′C′;
当添加AC=∠A′C′可利用“SAS”判断△ABC≌△A′B′C′.
故答案为:∠B=∠B′或∠C=∠C′或AC=A′C′.
19.解:若乙说的是假话,则乙周日说的是真话,则甲和丙都在周日说真话,即周二丙说话是谎话,则丙在周一说的是真话,前后矛盾,则乙说的是假话不成立;
若乙说的是真话,则乙周一说的是真话,则甲和丙都在周一说真话,即周二丙说话是谎话,则丙在周一说的是真话,前后不矛盾,所以乙说的是真话;
故答案为:一.
20.解:∵OP平分∠AOB,
∴∠MOB=2∠BOP=64°,
由长方形直尺可知:
MP∥OB,
∴∠AMP=∠MOB=64°,
故答案为:64.
三.解答题
21.解:∵点C在AE的垂直平分线上,
∴CA=CE,
∵AD⊥BE,BD=DC,
∴AB=AC,
∵△ABC的周长为18,
∴AB+BC+AC=18,
∴2AC+2DC=18,
∴AC+DC=9,
∴DE=DC+CE=AC+CD=9(cm).
22.解:(1)∵BE⊥AD,
∴∠EBD=90°,
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°﹣∠F=27°;
(2)∵△ACF≌△DBE,
∴CA=BD,
∴CA﹣CB=BD﹣BC,即AB=CD,
∵AD=11cm,BC=5cm,
∴AB+CD=11﹣5=6cm,
∴AB=3cm.
23.解:∵AB=AC,
∴∠B=∠C,
∵CD=DA
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
设∠B=α,
则∠BDA=∠BAD=2α,
又∵∠B+∠BAD+∠BDA=180°,
∴α+2α+2α=180°,
∴α=36°,
∴∠B=36°.
24.证明:∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠EBF=90°,
∴∠CBF=90°﹣∠CBE,
∴∠DBF=180°﹣90°﹣∠ABE=90°﹣∠CBE=∠CBF.
即BF平分∠CBD.
25.解:(1)∵每场比赛胜者得三分,平局各得一分,败者不得分
∴每场比赛最多得3分,
又四个队之间需要打比赛12场,
∴这四支队的总得分之和最多有3×12=36分;
(2)甲专家的预测正确.
若得11分不出线,则必为第三名,故前两名至少也得11分,
而最后一名至少得3分,故各队之和至少有36分,
由(1)可知比赛中没有平局,
而中国队已经得了11分,所以必有平局,
故不可能,所以必出线.
26.证明:(1)∵在△ADB和△ADC中,
,
∴△ADB≌△ADC(AAS),
∴AB=AC;
(2)∵△ADB≌△ADC,
∴AB=AC,BD=CD,
∴A和D都在线段BC的垂直平分线上,
∴AD是线段BC的垂直平分线,
即AD⊥BC.
27.解:如图,线段A′B′即为所求.
全等三角形》单元测试卷
一.选择题
1.△ABC中,∠B=50°,∠A=80°,若AB=6,则AC=( )
A.6
B.8
C.5
D.13
2.下列命题中真命题的个数是( )
①关于某直线对称的两个三角形是全等三角形;
②圆的直径是圆的对称轴;
③有两个角是60°的三角形是等边三角形;
④顶角和底角相等的等腰三角形是等边三角形.
A.1
B.2
C.3
D.4
3.如图,△AEC≌△ADB,若∠A=50°,∠ABD=38°,则图中∠AEC的度数是( )
A.88°
B.92°
C.95°
D.102°
4.在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件后能用“SAS”判定△ABC≌△A′B′C′的是( )
A.AC=A′C′
B.BC=B′C′
C.∠B=∠B′
D.∠C=∠C′
5.如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
A.当β为定值时,∠CDE为定值
B.当α为定值时,∠CDE为定值
C.当γ为定值时,∠CDE为定值
D.无法确定
6.如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1度数为( )
A.∠1=20°
B.∠1=60°
C.∠1=40°
D.无法判断
7.如图,△ABC,点D在AC上,连接BD,∠ABD=2∠DBC,∠ADB=2∠C,∠DBC=∠A,则图中共有等腰三角形( )个.
A.0
B.1
C.2
D.3
8.图书馆将某一本书和某一个关键词建立联系,规定:当关键词Ai出现在书Bj中时,元素aij=1,否则aij=0(i,j为正整数).例如:当关键词A1出现在书B4中时,a14=1,否则a14=0.根据上述规定,某读者去图书馆寻找书中同时有关键词“A2,A5,A6”的书,则下列相关表述错误的是( )
A.当a21+a51+a61=3时,选择B1这本书
B.当a22+a52+a62<3时,不选择B2这本书
C.当a2j,a5j,a6j全是1时,选择Bj这本书
D.只有当a2j+a5j+a6j=0时,才不能选择Bj这本书
9.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③
B.①②④
C.②③④
D.①②③④
10.在以如图形中,根据尺规作图痕迹,能判断射线AD平分∠BAC的是( )
A.图1和图2
B.图1和图3
C.图3
D.图2和图3
二.填空题
11.如图,在△ABC中,直线l垂直平分BC,射线m平分∠ABC,且l与m相交于点P,若∠A=60°,∠ACP=24°,则∠ABP=
°.
12.已知∠AOB=40°,OC是∠AOB的平分线,则∠AOC等于
.
13.若实数m、n满足|m﹣3|+=0,且m,n恰好是等腰△ABC的两条边的边长,则△ABC的周长是
.
14.如图,△ABC≌△DBC,∠A=45°,∠DCB=43°,则∠ABC=
.
15.如图,AC⊥BC,AD⊥BD,垂足分别是C,D,(若要用“HL”得到Rt△ABC≌Rt△BAD,则应添加的条件是
.(写一种即可)
16.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,∠B=∠E,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是
(只需写一个,不添加辅助线).
17.若等边三角形的一边上的高为6,则它的边长为
.
18.在△ABC和△A′B′C′中,若∠A=∠A′,AB=A′B′,请你补充一个条件
,使得△ABC≌△A′B′C′.
19.甲乙丙三个人在一起聊天,每周从星期一到星期日每人连续两天说谎(包括星期日和星期一),其余五天必说真话,且任意两人不会在同一天说谎.已知周一时,乙说:“我昨天说谎了.”周二时,丙说:“太巧了,我昨天也说谎了.”则三个人都没说谎的是星期
.
20.高兴同学在学习了全等三角形的相关知识后发现:只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图,一把直尺压住射线OB且与射线OA交于点M,另一把直尺压住射线OA且与第一把直尺交于点P,则OP平分∠AOB.若∠BOP=32°,则∠AMP=
°.
三.解答题
21.如图,在△ABE中,AD⊥BE于点D,C是BE上一点,BD=DC,且点C在AE的垂直平分线上,若△ABC的周长为18cm,求DE的长.
22.如图,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.
(1)若BE⊥AD,∠F=63°,求∠A的大小.
(2)若AD=11cm,BC=5cm,求AB的长.
23.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,求∠B的度数.
24.如图所示,已知BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.
25.世界预选赛中,中国、澳大利亚、卡塔尔和伊拉克被分在A组,进行主客场比赛.规定每场比赛胜者得三分,平局各得一分,败者不得分.比赛结束后前两名可以晋级.由于4支队伍均为强队,每支队伍至少得3分.于是甲专家预测:中国队只要得11分就能确保出线.
问:(1)这四支队的总得分之和最多有几分?
(2)甲专家的预测正确吗?为什么?
26.如图,∠ADB=∠ADC,∠B=∠C.
(1)求证:AB=AC;
(2)连接BC,求证:AD⊥BC.
27.尺规作图:如图,已知线段AB,求作线段A'B',使A'B'=AB.
参考答案与试题解析
一.选择题
1.解:∵△ABC中,∠B=50°,∠A=80°,
∴∠C=180°﹣∠A﹣∠B=180°﹣80°﹣50°=50°,
∴∠C=∠B,
∴AC=AB=6,
故选:A.
2.解:①关于某直线对称的两个三角形是全等三角形,是真命题;
②圆的直径所在的直线是圆的对称轴,本小题说法是假命题;
③有两个角是60°的三角形是等边三角形,是真命题;
④顶角和底角相等的等腰三角形是等边三角形,是真命题;
故选:C.
3.解:在△ABD中,∠A=50°,∠ABD=38°,
∴∠ADB=180°﹣∠A﹣∠ABD=92°,
∵△AEC≌△ADB,
∴∠AEC=∠ADB=92°,
故选:B.
4.解:添加AC=A'C'后能用“SAS”判定△ABC≌△A′B′C′.
在△ABC和△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS).
故选:A.
5.解:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
又∵∠ADC=∠B+∠BAD=∠B+∠α,∠AED=∠C+∠CDE,
∴∠ADE+∠CDE=∠B+∠BAD=∠B+∠α,
即∠C+∠CDE+∠CDE=∠B+∠α,
∴2∠CDE=∠α,
∴∠CDE=∠α.
即当∠α为定值时,∠CDE为定值,
故选:B.
6.解:∵△BCD是等边三角形,
∴∠BDC=60°,
∵a∥b,
∴∠2=∠BDC=60°,
由三角形的外角性质和对顶角相等可知,∠1=∠2﹣∠A=40°,
故选:C.
7.解:图中共有等腰三角形3个,理由如下:
∵∠ADB=∠C+∠DBC,∠ADB=2∠C,
∴∠DBC=∠C,
∴△BCD是等腰三角形,DB=DC,
∵∠ABD=2∠DBC,
∴∠ABD=∠ADB,
∴△ABD是等腰三角形,AB=AD,
∵∠DBC=∠A,
∴∠A=∠C,
∴△ABC是等腰三角形,AB=CB,
故选:D.
8.解:根据题意aij的值要么为1,要么为0,
A、a21+a51+a61=3,说明a21=1,a51=1,a61=1,故关键词“A2,A5,A6”同时出现在书B1中,
而读者去图书馆寻找书中同时有关键词“A2,A5,A6”的书,故A表述正确;
B、当a22+a52+a62<3时,则a22、a52、a62时必有值为0的,即关键词“A2,A5,A6”不同时具有,
从而不选择B2这本书,故B表述正确;
C、当a2j,a5j,a6j全是1时,则a2j=1,a5j=1,a6j=1,故关键词“A2,A5,A6”同时出现在书Bj中,
则选择Bj这本书,故C表述正确;
D、根据前述分析可知,只有当a2j+a5j+a6j=3时,才能选择Bj这本书,而a2j+a5j+a6j的值可能为0、1、2、3,
故D表述错误,符合题意.
故选:D.
9.解:∵在△ABC中,∠ACB=90°,DE⊥AB,
∴∠ADE=∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∵∠DCA=∠DAC,
∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD,
∵AD=CD,
∴CD=AB;故②正确;
∠DCA=∠DAC,
∴AD=CD,
但不能判定△ADC是等边三角形;故③错误;
∵若∠E=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ADC=60°,
∵∠ADE=∠ACB=90°,
∴∠EDC=∠BCD=∠B=30°,
∴CF=DF,
∴DE=EF+DF=EF+CF.故④正确.
故选:B.
10.解:在图1中,利用基本作图可判断AD平分∠BAC;
在图2中,根据作法可知:
AE=AF,AM=AN,
在△AMF和△ANE中,
,
∴△AMF≌△ANE(SAS),
∴∠AMD=∠AND,
∵∠MDE=∠NDF,
∵AE=AF,AM=AN,
∴ME=NF,
在△MDE和△NDF中,
,
∴△MDE≌△NDF(AAS),
所以D点到AM和AN的距离相等,
∴AD平分∠BAC.
在图3中,利用基本作图得到D点为BC的中点,则AD为BC边上的中线;
故选:A.
二.填空题
11.解:∵BP平分∠ABC,
∴∠ABP=∠CBP,
∵直线l是线段BC的垂直平分线,
∴BP=CP,
∴∠CBP=∠BCP,
∴∠ABP=∠CBP=∠BCP,
∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°,
∴3∠ABP+24°+60°=180°,
解得:∠ABP=32°,
故答案为:32.
12.解:∵OC是∠AOB的平分线,∠AOB=40°,
∴∠AOC=∠AOB=×40°=20°,
故答案为:20°.
13.解:∵|m﹣3|+=0,
∴m﹣3=0,n﹣4=0,
解得m=3,n=4,
当m=3作腰时,三边为3,3,4,符合三边关系定理,周长为:3+3+4=10,
当n=4作腰时,三边为,3,4,4,符合三边关系定理,周长为:3+4+4=11.
故答案为:10或11.
14.解:∵△ABC≌△DBC,
∴∠ACB=∠DCB=43°,
∵∠A=45°,
∴∠ABC=180°﹣∠A﹣∠ACB=92°,
故答案为:92°.
15.解:若添加AC=BD,在Rt△ABC和Rt△BAD中,,
∴Rt△ABC≌Rt△BAD(HL);
若添加BC=AD,在Rt△ABC和Rt△BAD中,,
∴Rt△ABC≌Rt△BAD(HL).
故答案为:AC=BD或BC=AD.
16.解:添加AB=ED,
∵BF=CE,
∴BF+FC=CE+FC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
故答案为:AB=ED(答案不唯一).
17.解:如图,
∵△ABC是等边三角形,且高AD=6,
∴∠ADC=90°,BD=CD=AC,
设它的边长为x,可得x2=()2+62,
解得:x=4,x=﹣4(舍去),
故答案为:4.
18.解:在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,
当添加∠B=∠B′可利用“ASA”判断△ABC≌△A′B′C′;
当添加∠C=∠C′可利用“AAS”判断△ABC≌△A′B′C′;
当添加AC=∠A′C′可利用“SAS”判断△ABC≌△A′B′C′.
故答案为:∠B=∠B′或∠C=∠C′或AC=A′C′.
19.解:若乙说的是假话,则乙周日说的是真话,则甲和丙都在周日说真话,即周二丙说话是谎话,则丙在周一说的是真话,前后矛盾,则乙说的是假话不成立;
若乙说的是真话,则乙周一说的是真话,则甲和丙都在周一说真话,即周二丙说话是谎话,则丙在周一说的是真话,前后不矛盾,所以乙说的是真话;
故答案为:一.
20.解:∵OP平分∠AOB,
∴∠MOB=2∠BOP=64°,
由长方形直尺可知:
MP∥OB,
∴∠AMP=∠MOB=64°,
故答案为:64.
三.解答题
21.解:∵点C在AE的垂直平分线上,
∴CA=CE,
∵AD⊥BE,BD=DC,
∴AB=AC,
∵△ABC的周长为18,
∴AB+BC+AC=18,
∴2AC+2DC=18,
∴AC+DC=9,
∴DE=DC+CE=AC+CD=9(cm).
22.解:(1)∵BE⊥AD,
∴∠EBD=90°,
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°,
∴∠A=90°﹣∠F=27°;
(2)∵△ACF≌△DBE,
∴CA=BD,
∴CA﹣CB=BD﹣BC,即AB=CD,
∵AD=11cm,BC=5cm,
∴AB+CD=11﹣5=6cm,
∴AB=3cm.
23.解:∵AB=AC,
∴∠B=∠C,
∵CD=DA
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
设∠B=α,
则∠BDA=∠BAD=2α,
又∵∠B+∠BAD+∠BDA=180°,
∴α+2α+2α=180°,
∴α=36°,
∴∠B=36°.
24.证明:∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠EBF=90°,
∴∠CBF=90°﹣∠CBE,
∴∠DBF=180°﹣90°﹣∠ABE=90°﹣∠CBE=∠CBF.
即BF平分∠CBD.
25.解:(1)∵每场比赛胜者得三分,平局各得一分,败者不得分
∴每场比赛最多得3分,
又四个队之间需要打比赛12场,
∴这四支队的总得分之和最多有3×12=36分;
(2)甲专家的预测正确.
若得11分不出线,则必为第三名,故前两名至少也得11分,
而最后一名至少得3分,故各队之和至少有36分,
由(1)可知比赛中没有平局,
而中国队已经得了11分,所以必有平局,
故不可能,所以必出线.
26.证明:(1)∵在△ADB和△ADC中,
,
∴△ADB≌△ADC(AAS),
∴AB=AC;
(2)∵△ADB≌△ADC,
∴AB=AC,BD=CD,
∴A和D都在线段BC的垂直平分线上,
∴AD是线段BC的垂直平分线,
即AD⊥BC.
27.解:如图,线段A′B′即为所求.
