浙江省2016-2020年科学中考(物理)试题分类(7)——简单机械(含答案)
文档属性
| 名称 | 浙江省2016-2020年科学中考(物理)试题分类(7)——简单机械(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 539.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览


文档简介
1057910010261600
浙江省2016-2020年科学中考(物理)试题分类(7)——简单机械
一、单选题
1.(2019·嘉兴)为便于研究,某健身器材中训练拉力部分的机械结构可简化为如图所示的滑轮组。若不计摩擦,下列有关分析正确的是(?? )
A.?两个滑轮在装置中起的作用相同
B.?拉力移动的距离与配重上升的距离相同
C.?沿方向1与2匀速拉动配重,所用的力大小相等
D.?将配重提升相同高度,用该装置与直接提升所做的功相等
2.(2018·宁波)如图所示,F1=4N,F2=3N,此时物体A对于地面静止,物体B以0.1m/s的速度在物体A表面向左做匀速直线运动(不计弹簧测力计、滑轮和绳子的自重及滑轮和绳子之间的摩擦)。下列说法错误的是( ???)
A.?F2的功率为0.6W????????????????????????????????????????????????B.?弹簧测力计读数为9N
C.?物体A和地面之间有摩擦力?????????????????????????????????D.?如果增大F2 , 物体A可能向左运动
3.(2020·宁波)现有一根形变不计、长为L的铁条AB和两根横截面积相同、长度分别为La、Lb的铝条a、b。将铝条a叠在铁条AB上,并使它们的右端对齐,然后把它们放置在三角形支架O上,AB水平平衡,此时OB的距离恰好为La , 如图所示。取下铝条a后,将铝条b按上述操作方法使铁条AB再次水平平衡,此时OB的距离为Lx。下列判断正确的是( ?)
A.?若La La+Lb2 成立
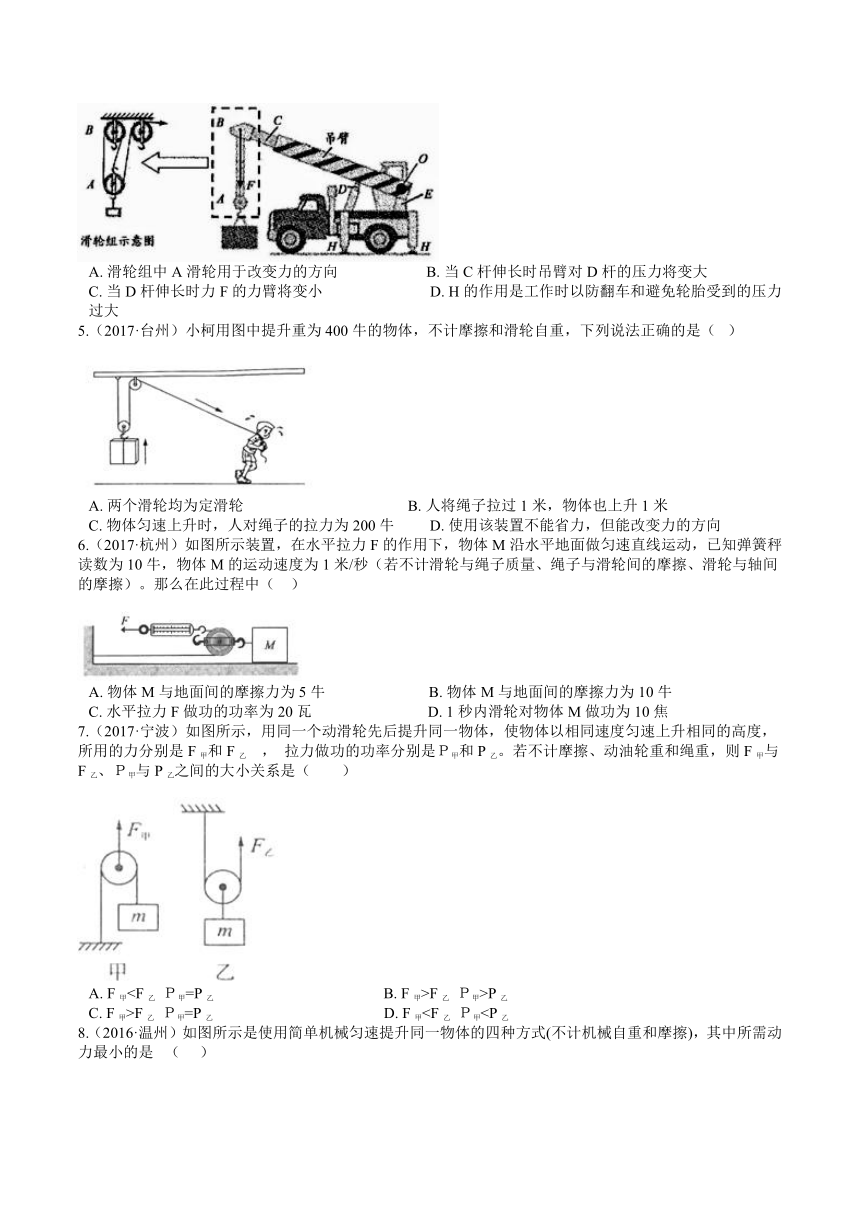
C.?若Lb4.(2018·衢州)如图所示是汽车起重机,其中A,B组成滑轮组(结构如示意图),C杆伸缩可改变吊臂的长短,D杆伸缩可改变吊臂与水平面的角度,O为吊臂的转动轴。装在E里的电动机牵引钢丝绳,利用滑轮组提升重物,H为在车身外侧增加的支柱,F为吊臂顶端受到竖直向下的力。下列有关汽车起重机的叙述中错误的是(??? )
A.?滑轮组中A滑轮用于改变力的方向???????????????????????B.?当C杆伸长时吊臂对D杆的压力将变大
C.?当D杆伸长时力F的力臂将变小????????????????????????????D.?H的作用是工作时以防翻车和避免轮胎受到的压力过大
5.(2017·台州)小柯用图中提升重为400牛的物体,不计摩擦和滑轮自重,下列说法正确的是(? )
A.?两个滑轮均为定滑轮???????????????????????????????????????????B.?人将绳子拉过1米,物体也上升1米
C.?物体匀速上升时,人对绳子的拉力为200牛?????????D.?使用该装置不能省力,但能改变力的方向
6.(2017·杭州)如图所示装置,在水平拉力F的作用下,物体M沿水平地面做匀速直线运动,已知弹簧秤读数为10牛,物体M的运动速度为1米/秒(若不计滑轮与绳子质量、绳子与滑轮间的摩擦、滑轮与轴间的摩擦)。那么在此过程中(?? )
A.?物体M与地面间的摩擦力为5牛???????????????????????????B.?物体M与地面间的摩擦力为10牛
C.?水平拉力F做功的功率为20瓦??????????????????????????????D.?1秒内滑轮对物体M做功为10焦
7.(2017·宁波)如图所示,用同一个动滑轮先后提升同一物体,使物体以相同速度匀速上升相同的高度,所用的力分别是F甲和F乙 , 拉力做功的功率分别是P甲和P乙。若不计摩擦、动油轮重和绳重,则F甲与F乙、P甲与P乙之间的大小关系是( )
A.?F甲F乙? P甲>P乙
C.?F甲>F乙? P甲=P乙???????? ??????????????????????????????????????D.?F甲8.(2016·温州)如图所示是使用简单机械匀速提升同一物体的四种方式(不计机械自重和摩擦),其中所需动力最小的是? (? ??)
A.?????????????B.?????????????C.?????????????D.?
9.(2016·缙云)如图,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块Q相连,从滑轮到P和到Q的两段绳都是水平的。已知Q与P之间以及P与桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮的质量、滑轮轴上的摩擦都不计。已知滑动摩擦力f与压力F压之间的关系为f=μF压,若用一水平向右的力F拉着P使它做匀速运动,则F的大小为(???? )
A.?4μmg??????????????????????????????????B.?3μmg??????????????????????????????????C.?2μmg??????????????????????????????????D.?μmg
10.(2016·缙云)为模拟盘山公路,现将连接了重1N小球的细线穿入一根长1m的细管。如图,将细管从竖直放置的圆柱体底部a点开始斜向上缠绕5圈后,恰好绕至顶部b点,相邻细管间的高度均为12cm。在b点处通过细线用0.8N的拉力(与管的轴线平行)将管口的小球从a点匀速拉至b点。则缠绕在圆柱体上的细管(模拟的盘山公路)的机械效率为(???? )
A.?83.3%????????????????????????????????????B.?80%????????????????????????????????????C.?75%????????????????????????????????????D.?60%
11.(2017·丽水)如图所示,使用时属于费力杠杆的是(??? )
A.?镊子夹石块????????????B.?起子开瓶盖????????????C.?羊角锤拔铁钉????????????D.?天平称物体质量
12.(2017·嘉兴)如图是一种切甘蔗用的铡刀示意图。下列有关说法正确的是(?? )
A.?刀刃很薄可以增大压力???????????????????????????????????????B.?铡刀实质上是一种费力杠杆
C.?甘蔗放在a点比b点更易被切断????????????????????????????D.?手沿F1方向用力比沿F2方向更省力
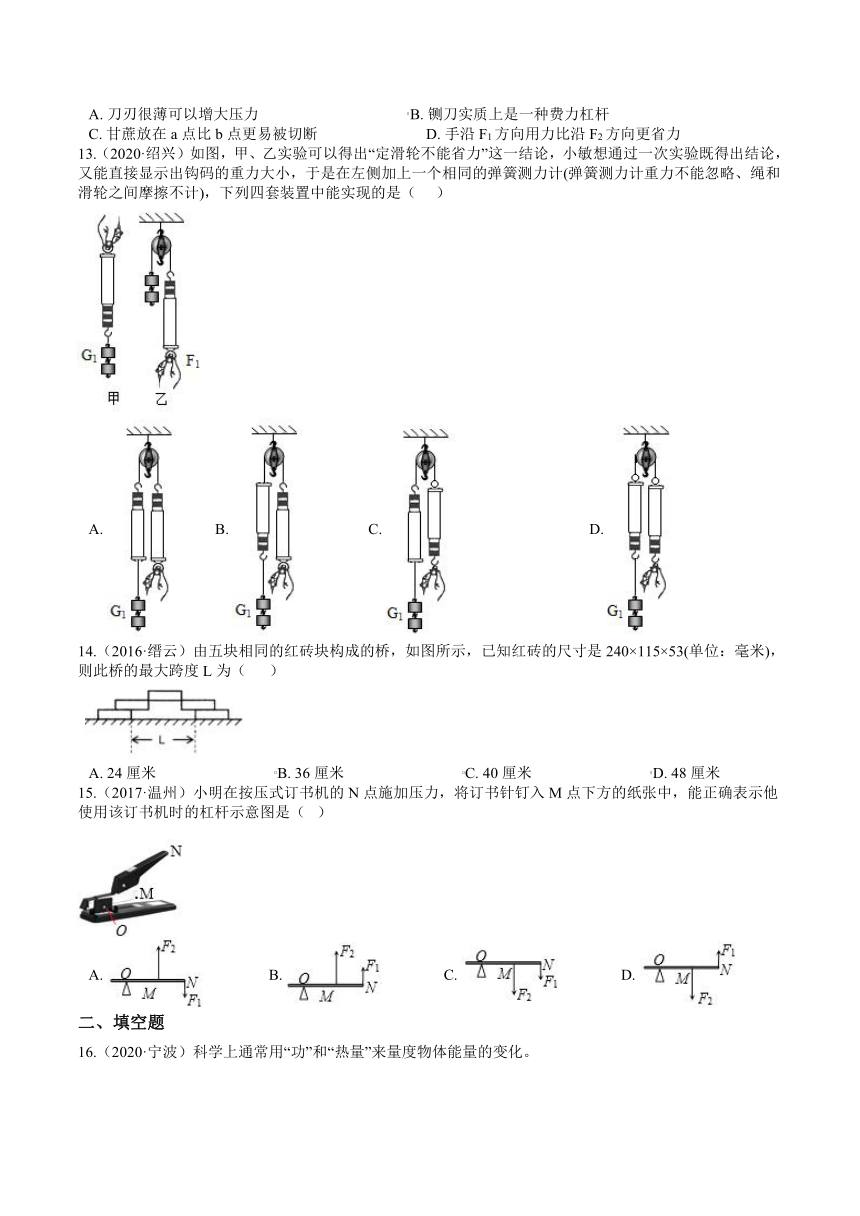
13.(2020·绍兴)如图,甲、乙实验可以得出“定滑轮不能省力”这一结论,小敏想通过一次实验既得出结论,又能直接显示出钩码的重力大小,于是在左侧加上一个相同的弹簧测力计(弹簧测力计重力不能忽略、绳和滑轮之间摩擦不计),下列四套装置中能实现的是( ???)
A.????????B.?????????????????C.??????????????????????????????D.?
14.(2016·缙云)由五块相同的红砖块构成的桥,如图所示,已知红砖的尺寸是240×115×53(单位:毫米),则此桥的最大跨度L为(???? )
A.?24厘米???????????????????????????????B.?36厘米???????????????????????????????C.?40厘米???????????????????????????????D.?48厘米
15.(2017·温州)小明在按压式订书机的N点施加压力,将订书针钉入M点下方的纸张中,能正确表示他使用该订书机时的杠杆示意图是(? )
A.?????????????????B.?????????????????C.?????????????????D.?
二、填空题
16.(2020·宁波)科学上通常用“功”和“热量”来量度物体能量的变化。
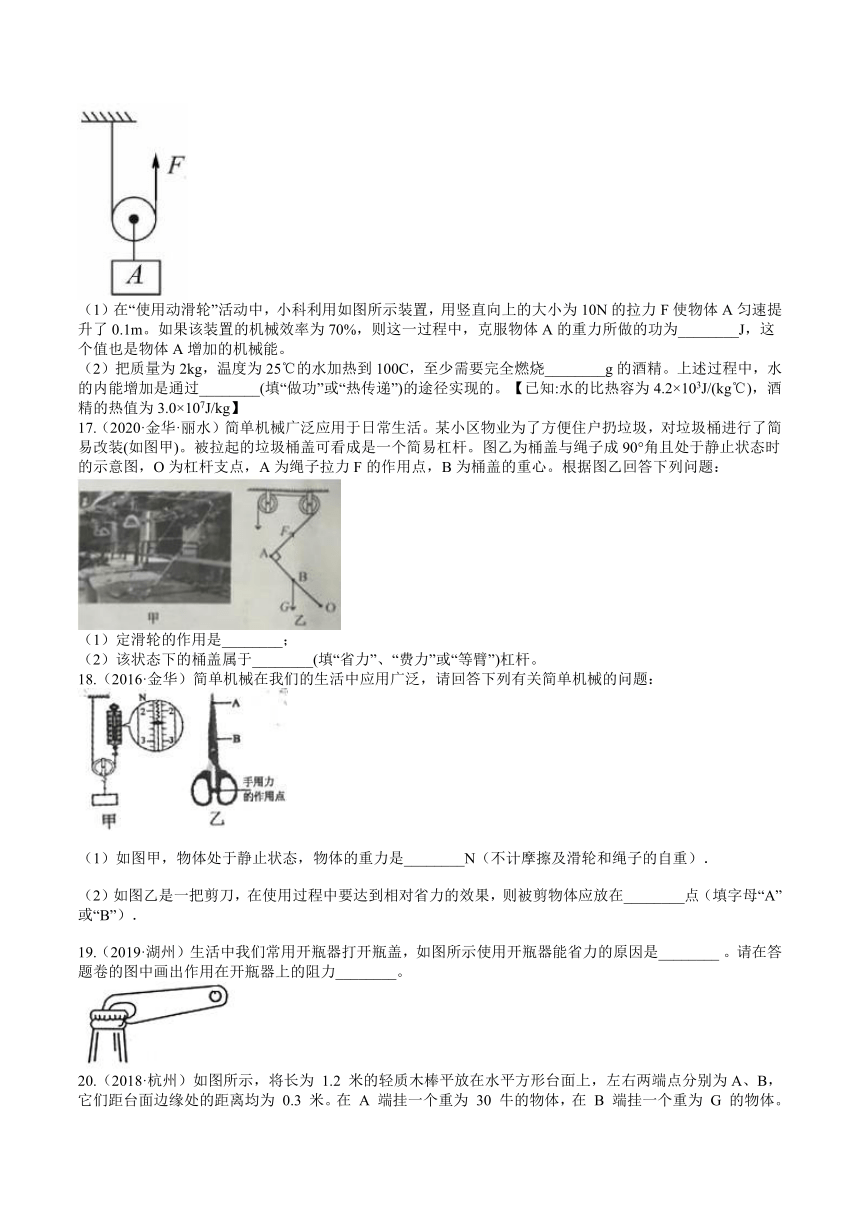
(1)在“使用动滑轮”活动中,小科利用如图所示装置,用竖直向上的大小为10N的拉力F使物体A匀速提升了0.1m。如果该装置的机械效率为70%,则这一过程中,克服物体A的重力所做的功为________J,这个值也是物体A增加的机械能。
(2)把质量为2kg,温度为25℃的水加热到100C,至少需要完全燃烧________g的酒精。上述过程中,水的内能增加是通过________(填“做功”或“热传递”)的途径实现的。【已知:水的比热容为4.2×103J/(kg℃),酒精的热值为3.0×107J/kg】
17.(2020·金华·丽水)简单机械广泛应用于日常生活。某小区物业为了方便住户扔垃圾,对垃圾桶进行了简易改装(如图甲)。被拉起的垃圾桶盖可看成是一个简易杠杆。图乙为桶盖与绳子成90°角且处于静止状态时的示意图,O为杠杆支点,A为绳子拉力F的作用点,B为桶盖的重心。根据图乙回答下列问题:
(1)定滑轮的作用是________;
(2)该状态下的桶盖属于________(填“省力”、“费力”或“等臂”)杠杆。
18.(2016·金华)简单机械在我们的生活中应用广泛,请回答下列有关简单机械的问题:
(1)如图甲,物体处于静止状态,物体的重力是________N(不计摩擦及滑轮和绳子的自重).
(2)如图乙是一把剪刀,在使用过程中要达到相对省力的效果,则被剪物体应放在________点(填字母“A”或“B”).
19.(2019·湖州)生活中我们常用开瓶器打开瓶盖,如图所示使用开瓶器能省力的原因是________?。请在答题卷的图中画出作用在开瓶器上的阻力________。
20.(2018·杭州)如图所示,将长为 1.2 米的轻质木棒平放在水平方形台面上,左右两端点分别为A、B,它们距台面边缘处的距离均为 0.3 米。在 A 端挂一个重为 30 牛的物体,在 B 端挂一个重为 G 的物体。
(1)若 G=30 牛,台面收到木棒的压力为________牛。
(2)若要使木棒右端下沉,B 端挂的物体至少要大于________牛。
(3)若 B 端挂物体后,木棒仍在水平台面上静止,则 G 的取值范围为________牛。
21.(2017·衢州)如图为小柯制作的“杠杆力臂演示仪”,杠杆AOB可绕O点(螺母)转动,OA=0.2m,OB=0.1m,G1=2N,杠杆自身重力和摩擦不计,固定装置未画出。
(1)当杠杆处于甲图所示水平位置平衡时,G2的重力为________N。
(2)松开螺母保持OA不动,使OB向下折一个角度后,再拧紧螺母形成一根可绕O点转动的杠杆AOB'? (B'点对应B点),保持G1位置不变,要使杠杆在图乙位置保持平衡,则G2应该移动到__________。
A.B’点处
B.① 点处
C.②点处
D.③点处
22.(2017·杭州)小金将长为0.6米、质量可忽略不计的木棒搁在肩上,棒的后端A挂一个40牛的物体,肩上支点O离后端A为0.2米,他用手压住前端B使木棒保持水平平衡,如图所示。小金的质量为50千克,则此时手压木棒的力大小为________牛,肩对木棒的支持力大小为________牛,人对地面的压力大小为________牛(g=10牛/千克)。
三、实验探究题(共1题;共3分)
23.(2016·缙云)如图所示为小明自制的风力板,a板为迎风板,其迎风面承受风力,b板为压重板,它水平放置,m为压重板上的铁板(a、b板重力不计)。当压重板上铁板重力一定时,风力大到一定程度,风力板就会倾倒。小明通过查阅资料和实验,在压重板上加上重力不同的铁板,制成能测风力1~8级的8个风力板,构成一套风力探测仪。在南风盛行的某地,小明用这套风力探测仪测定当天最强的风力。
(1)压重板上的铁板越重,风力板倾倒时记录的风力越________。
(2)在开阔地的水平地面放置风力探测仪时,小明应________。
(3)小明确定当天最强风力的方法是________。
四、解答题
24.(2020·台州)晾衣架(如图)给日常生活带来许多方便,转动手摇器能使横杆上升或下降
(1)安装在天花板上虚线框内的简单机械应是________。
(2)使用一段时间后,对手摇器的转轴添加润滑剂,目的是________。
(3)将挂在晾衣架上重为20牛的衣服升高1.5米,至少对衣服做多少功?
(4)由于使用不当.造成晾衣架右侧钢丝绳受损,最多只能承受15牛的力,左侧钢丝绳能正常使用。晾衣架的横杆上有11个小孔,相邻两孔间的距离均为20厘米。现准备将重为20牛的一件衣服挂到水平横杆的小孔进行晾晒,通过计算说明挂在哪些编号的小孔,在侧钢丝绳会断裂(横杆、衣架和钢丝绳等自重不计)。
25.(2018·湖州)在拓展课上,小泉同学模拟某建筑工地上拉动工件的情景,设置了如图所示的滑轮组。他用该滑轮组在4秒内将一个重为100牛的物体,沿着水平地面匀速拉动了2米。人的拉力为18牛,物体移动时受到地面的摩擦力为物重的0.35倍,不计绳重及机械的摩擦。求:
(1)人的拉力所做的功。
(2)人的拉力做功的功率。
(3)动滑轮受到的重力。
26.(2017·湖州)建筑工人利用如图所示装置,将质量为100千克的沙袋从地面匀速提到3米高的一楼楼面,用时30秒.已知动滑轮的质量为8千克,不计绳子重力和摩擦.
求:
(1)拉力的大小.
(2)这段时间内人拉绳子做功的功率.
27.(2016·缙云)某同学为了体验“南海一号”的打捞过程,特利用滑轮组从水下打捞一重物.如图所示,用一个底面积S=0.05m2 , 高h=0.2m的长方体形状的重物模拟“南海一号”,该同学站在岸边拉动绳子的自由端,使重物从水底开始向上运动.假定重物一直做竖直向上的匀速直线运动,并经历三个运动阶段:第一阶段,从重物在水底开始运动到重物的上表面刚露出水面,绳对重物的拉力F1=140N,用时t1=40s;第二阶段,从重物上表面刚露出水面到其下表面刚离开水面,用时t2=4s;第三阶段,从重物下表面离开水面后在空中上升。已知动滑轮所受重力G=60N,ρ水=1.0×103kg/m3 , g=10N/kg,不计绳重、轮与轴之间的摩擦及水的阻力,不考虑重物出水前后质量的变化.求:
(1)在第一阶段运动中,水对重物的浮力F浮为多大?
(2)在第一阶段运动中,绳对重物做功W1为多大?
(3)滑轮在第一阶段运动中的机械效率η1和在第三阶段运动中的机械效率η3分别为多大?
28.(2016·杭州)小金用如图所示的实验装置测量杠杆的机械效率.实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升.(支点和杠杆的摩擦不计)问:
(1)重为5N的钩码挂在A点时,人的拉力F为4N,钩码上升0.3m时,动力作用点C上升0.5m,此时机械效率η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m.问:人的拉力F与第一次相比??????? (选填“变大”“变小”或“不变”).比较此时的机械效率η2与η1的大小并用学过的知识给以推导.
29.(2020·杭州)杆秤是一种用来测量物体质量的工具。小金尝试做了如图所示的杆秤。在秤盘上不放重物时,将秤砣移至O点提纽处,杆秤恰好水平平衡,于是小金将此处标为0刻度。当秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡测得OA=5cm,OB=10cm。
(1)计算秤砣的质量
(2)小金在B处标的刻度应为________kg。若图中OC=2OB,则C处的刻度应为________Kg
(3)当秤盘上放一个质量为2kg的物体时,若换用一个质量更大的秤砣,移动秤砣使杆秤再次水平平衡时,其读数________(选填“<”或“>”)2kg,由此可知一杆杄秤不能随意更换秤砣
30.(2019·杭州)如图甲,有一轻质杆,左右各挂由同种金属制成,质量分别为m1和m2(m1>m2)的实心物块后恰好水平平衡
(1)求左右悬挂点到支点O的距离L1与L2之比
(2)将两物分别浸没在水中,杆将会?? ▲?? (选填“左端下降”“右端下降”“仍然平衡”),试通过推导说明。
31.(2018·台州)图甲是一种壶口处配有自动开合小壶盖的电水壶。
(1)如图乙,电水壶底部的导线连接装置有铜环①、铜环②和铜柱③。经测试发现:①、②之间是绝缘的,②、③之间常温下有十几欧姆的电阻。则与水壶金属外壳相连的装置是________。
(2)图丙是自动开合小壶盖简化侧视图。OA是小壶盖,C是其重力作用点。B是小壶盖的配重。OB是配重柄。AOB能绕固定点O自由转动。请在答题纸图丙中作出小壶盖的重力G及其力臂L。
(3)已知:小壶盖质量为4克,OA=3厘米,OC=1.4厘米,OB=1厘米,∠AOB=135°.要求倒水时,壶身最多倾斜45°,小壶盖便自动打开;壶身竖直时,小壶盖在水平位置自动闭合。求配重B的质量取值范围。(配重柄质量和O点的摩擦均忽略不计, 2 取1.4)
32.(2018·绍兴)2018年3月28日绍兴风情旅游新干线开通试运行。“鉴湖号”城际列车从绍兴站驶出开往上虞站,两站相距40千米,列车运营速度120千米/小时.
(1)列车从绍兴站出发至少需要________分钟到达上虞站。
(2)在图中旅行箱和拉杆构成的杠杆中,能表示拉力F的力臂是________。
(3)列车牵引总功率为5152千瓦,表示的意义是________,并计算列车以运营速度匀速直线运行时所受水平阻力大小________(用科学计数法表示,保留两位小数)。
33.(2016·台州)桥式起重机在工业生产上有广泛应用.如图是某桥式起重机的示意图,水平横梁MN架在轨道A和B上,电动机D可沿横梁左右移动.横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计.
(1)电动机通过滑轮组,将质量为600千克的零件,以0.4米/秒的速度匀速吊高4米.求:电动机对零件做的功为多少焦?电动机的功率至少为多少瓦?(g取10牛/千克)
(2)已知横梁长度为L,零件质量为m,电动机吊着零件从M点出发并开始计时,以水平速度v匀速运动到N点,横梁对轨道A的压力F与时间t的关系式为:F=________.
34.(2016·衢州)如图为小柯在科技节中制作的“杠杆力臂演示仪”和“流体压强与流速关系演示仪”.
(1)如图甲(杠杆自身质量和摩擦忽略不计,固定装置未画出),O为支点,OA=OD=3OB=0.6米,CD=0.2米.在做背景的白纸上作有以O为圈心半径为0.2米的圆.在A点挂5牛顿的重物G,要使杠杆水平平衡,则作用在B点竖直向下的力FB应为________牛,撤去FB后,按图示方向分别施加FC、FD两个力,且毎次都使杠杆在水平位置平衡,则FC、FD大小关系为________.
(2)如图乙,在注射器A、B处分别扎一个等大的小孔,插入两根相同规格的硬质塑料管(连接处密封),并 在管上分别系一个未充气的同规格气球(连接处不漏气).先慢慢往外拉活塞,使注射器中充满空气,接着快速向内推动活塞,在此过程中可现察到A、B两孔处气球的鼓起情况是________(填序号).
①A孔处气球大②B孔处气球大③两个气球一样大
35.(2016·嘉兴)如图甲为塔式起重机简易示意图,塔式起重机主要用于房屋建筑中材料的输送及建筑构件的安装.(动滑轮重、绳重及摩擦均不计,g取10牛/千克)
(1)为保持平衡,起重臂的长度越长的塔式起重机,配备的平衡重的质量应越________.
(2)图乙为起重机钢丝绳穿绳简化示意图,滑轮a的作用是________.若钢丝绳能承受的最大拉力为3×104牛,则能吊起货物的质量不能超过________千克?
(3)若将重为1.2×104牛的货物由地面沿竖直方向匀速提升30米,再沿水平方向移动20米,则此过程中克服货物重力做功多少焦?
(4)若该起升电动机的效率为90%,将重为1.2×104牛的货物提升到30米的高度,用时50秒,则该起升电动机的实际功率是多少瓦?
答案解析部分
一、单选题
1.【答案】 C
【解析】【分析】(1)通过判断滑轮的种类判断它们的作用是否相同;
(2)使用滑轮组提升重物时,自由端的距离和物体上升高度之间的关系为:s=nh;
(3)定滑轮不省力不费力,且与拉力的方向无关;
(4)使用滑轮组时,要克服动滑轮的重力做功。
【解答】A.下面的滑轮是动滑轮,上面的滑轮是定滑轮,二者的作用不同,故A错误;
B.因为动滑轮上有2段绳子承担物重,因此拉力移动的距离是配重移动距离的2倍,故B错误;
C.使用定滑轮不省力不费力,且拉力的大小与方向无关,故C正确;
D.将配重提升相同高度,直接做的功为W=Gh,用该装置做的功为:W=(G+G动)h,因此二者不同,故D错误。
故选C。
2.【答案】 D
【解析】【分析】(1)功率计算公式P=Fv;(2)弹簧测力计的读数有拉着左侧滑轮的三根绳子决定;(3)由物体B的运动,判断出A对B有摩擦力,根据力的作用是相互的所以B对A也有摩擦力,根据A相对于地面静止可判断出A和地面之间是否有摩擦力;(4)滑动摩擦力的大小只与压力大小和表面粗糙程度有关,与B物体的运动速度无关。
【解答】A.F2的功率为0.6W,将左侧滑轮看成定滑轮时,这个滑轮组能省1/2的力,费2倍的距离,所以绳子自由端的运动速率为0.2m/s,由公式P=Fv=3N×0.2m/s=0.6W,说法正确,A错误;
B.弹簧测力计读数为9N,左侧滑轮有三根绳子拉着,每根绳的拉力都为3N,所以总拉力是9N,说法正确,B错误;
C.物体A和地面之间有摩擦力,因为B受到向左的拉力,向左做匀速直线运动,可知B受到平衡力的作用,B受到向左的拉力为6N,受到向右的摩擦力也为6N。由于力的作用是相互的,B也给A一个摩擦力且大小也为6N,方向向左,由于A保持静止所以A受到平衡力的作用,向应该受到向右的力也为6N,已知F1=4N,所以地面对A的摩擦力为2N方向向右,说法正确,C错误;
D.如果增大F2 , 物体A可能向左运动,由于滑动摩擦力的大小只与表面粗糙程度和压力的大小有关,而B对A的压力不变且粗糙程度也不变,所以滑动摩擦力不变,A物体的受力不变,所以仍为静止,说法错误,D正确。
故答案为:D
3.【答案】 A
【解析】【分析】根据杠杆的平衡条件分析。
【解答】当把铝条a放在铁条上时,铁条的重力G铁为阻力,作用在中点,那么阻力臂为:L2-La;动力为铝条a的重力Ga , 作用在它的中点处,动力臂为La2 ,
根据杠杆的平衡条件得到:G铁×L2-La=Ga×La2? ?①;
当把铝条b放在铁条上时,铁条的重力G铁为阻力,作用在中点,那么阻力臂为:L2-Lx;动力为铝条a的重力Ga , 作用在它的中点处,动力臂为Lx-Lb2 ,
根据杠杆的平衡条件得到:G铁×L2-Lx=Gb×Lx-Lb2 ②;
①÷②得到:
L2-LaL2-Lx=GaGb×La2Lx-Lb2 ③;
因为铝条a和b横截面积相等,根据公式G=ρVg=ρShg可知,铝条的重力与长度成正比,
即:GaGb=LaLb;
将其袋入③得到:L2-LaL2-Lx=LaLb×La2Lx-Lb2 ;
因为La 所以LaLb<1;
那么L2-LaL2-Lx 化简得到:L-2LaL-2Lx 整理得到:Lx 即:Lx 那么:Lx 如果支点O不动,因为Lb>La , 所以肯定后有一部分在O点左侧。与原来相比可知,此时左边重力增大,为了维持平衡,必须减小阻力臂,增大动力臂,即支点向左移动,那么La 故A正确,B错误;
若LbLa , 故C、D错误。
故选A。
4.【答案】 A
【解析】【分析】使用滑轮时,轴的位置固定不动的滑轮称为定滑轮。定滑轮不省力,但是可以改变力的方向。属于滑轮原理的应用,和机械功的讨论。实质上是动力臂等于阻力臂的杠杆。轴的位置随被拉物体一起运动的滑轮称为动滑轮。动滑轮实质是动力臂等于2倍阻力臂的杠杆(省力杠杆)。它不能改变力的方向,但最多能够省一半的力,但是不省功。
【解答】A、滑轮组中的A滑轮是动滑轮,动滑轮是用于省力的;故A错误;
B、 当C伸长时,阻力臂增长,而动力和动力臂不变,所以阻力会增大,则对D杆的压力会变大;故B正确;
C、 当D伸长时,倾斜角增大,所以力F的力臂会变小;故C正确;
D、 H杆的作用是用于支持起重机,防止压力作用在轮胎上;故D正确;
故答案为:A。
5.【答案】 C
【解析】【分析】此滑轮组是由一个定滑轮和一个动滑轮组成的,根据图中绕线可知能省力也能改变力的方向,但会比较费距离。
【解答】A.两个滑轮均为定滑轮,和物体一起上升的滑轮为动滑轮,A错误;
B.人将绳子拉过1米,物体也上升1米,滑轮组省力但费距离,当人拉过1米时,物体上升只有0.5米,B错误;
C.物体匀速上升时,人对绳子的拉力为200牛,此滑轮组能省 12 的力,F= 12 G,C正确;
D.使用该装置不能省力,但能改变力的方向,此滑轮组即能省力又能改变力的方向,D错误。
故选C
6.【答案】 C
【解析】【分析】本题所用滑轮组是水平的,计算过程要注意,拉力的大小是摩擦力的一半,拉力移动的路程是物体移动的路程的2倍(动滑轮由两股绳子拉着)。该滑轮为动滑轮,拉力F的大小和弹簧测力计的示数一样,因为物体做匀速运动,所以物体受到的力是平衡力,利用力的平衡可以计算摩擦力的大小;利用W=Fs公式计算拉力做的功,再利用功率的公式计算拉力F的功率。
【解答】∵物体做匀速运动,
∴摩擦力f=2F=2×10N=20N;故A、B错误;
v绳子=2v=2m/s,
水平拉力F做功的功率为P=Fv=10×2m/s=20W,故C正确;
s=vt=1s×1m/s=1m,
1秒内滑轮对物体M做功为W=Fs=20N×1m=20J,故D错误;
故选C
7.【答案】 C
【解析】【分析】不计摩擦、动滑轮重和绳重,对于动滑轮,F甲=2G,F乙= 12 G;根据P=Fv比较甲乙的功率.
【解答】解:
由题知,两装置都不计摩擦、动滑轮重和绳重,提升物体的重相同,
甲图,拉力作用在动滑轮的轴上,费一倍的力,即F甲=2G;
乙图,拉力作用在绳子自由端,省一半的力,即F乙= 12 G,故F甲>F乙 , AD错误;
物体上升的速度相同,则拉力端的速度分别为:v甲= 12 v物 , v乙=2v物 ,
甲图拉力的功率:P甲=F甲v甲=2G× 12 v物=Gv物;
乙图拉力的功率:P乙=F乙v乙= 12 G×2v物=Gv物 , 故P甲=P乙 , C正确,B错误;
故选C.
8.【答案】 D
【解析】【分析】由图示的斜面、滑轮组、动滑轮、杠杆分别求出拉力F1、F2、F3、F4 , 最后比较各力的大小,确定哪个拉力最小。
【解答】解:A、由图示的斜面知F1×L=G×h,F1×4m=G×2m,F1=12G;
B、由图示可知,滑轮组承重绳子的股数为3,拉力F2=G3;
C、这是动滑轮的特殊使用方法,物体挂在动滑轮一侧的绳子上,拉动滑轮的轮轴,此时拉力F3=2G;
D、由图可知L4∶LG=(1m+3m)∶1m=4∶1,由杠杆平衡条件可得:F4×L4=G×LG,F4=G×LGL4=G4;
因此最小拉力是F4。
故选D。
9.【答案】 A
【解析】【分析】(1)当P向右运动时,对于P而言,它受到的向左的阻力是地面给它的摩擦力,Q给它的摩擦力、定滑轮的绳子给它的拉力这三个力的总和。
(2)要使P做匀速运动,它受到向右的拉力与向左的阻力相互平衡。
【解答】以Q为研究对象, Q与P之间动摩擦因数是μ,物块的质量都是m, 所以Q给P的摩擦力也为f1=μmg;P做匀速运动,则Q也做匀速运动,由平衡条件可得绳子对Q的拉力为μmg,所以同一条定滑轮上的绳子给P的拉力也为μmg; P与桌面之间的动摩擦因数是μ,两物块的质量都是m,地面对P的滑动摩擦力大小f2=2μmg。F=T+f1+f2=μmg+μmg+2μmg=4μmg,A正确。
故答案为:A
?
10.【答案】 C
【解析】【分析】拉小球上升时,根据W有用=Gh计算有用功,根据W总=Fs计算总功,根据η=W有用W总×100%计算机械效率。
【解答】由题细管缠绕在圆体上后相当于一个斜面,由图a到b点的高度h=5×0.12m=0.6m,
拉小球上升时,有用功W有用=Gh=1N×0.6m=0.6J;总功W总=Fs=0.8N×1m=0.8J,
所以缠绕在圆柱体上的细管的机械效率:η=W有用W总×100%=0.6J0.8J×100%=75% , C正确。
故答案为:C
11.【答案】 A
【解析】【分析】杠杆的分类主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。结合生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆。
【解答】A、镊子在使用过程中,动力臂小于阻力臂,是费力杠杆,故A符合题意;
B、瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆,故B不符合题意;
C、羊角锤在使用过程中,动力臂大于阻力臂,是省力杠杆,故C不符合题意;
D、天平称物体质量,动力臂等于阻力臂,为了称量重量,故D不符合题意。
故选A
12.【答案】 C
【解析】【分析】杠杆可分为:省力杠杆、费力杠杆和等臂杠杆,可以从动力臂和阻力臂的大小关系进行判断,当动力臂大于阻力臂时,是省力杠杆;当动力臂等于阻力臂时,是等臂杠杆;当动力臂小于阻力臂时,是费力杠杆。
【解答】A、刀刃很薄是减小了受力面积,从而增大压强,故A错误;
B、铡刀当动力臂大于阻力臂时,是省力杠杆,故B错误;
C、甘蔗放在a点比b点阻力臂小,根据F1L1=F2L2 , 可知甘蔗放在a点比b点更易被切断,故C正确;
D、动力臂垂直于力的方向,可知F2动力臂大于F1 , 因此F2更省力,故D错误。
故选C
13.【答案】 D
【解析】【分析】使用滑轮时,轴的位置固定不动的滑轮称为定滑轮。定滑轮不省力,但是可以改变力的方向。属于滑轮原理的应用,和机械功的讨论。实质上是动力臂等于阻力臂的杠杆。控制变量在进行科学实验的概念,是指那些除了实验因素(自变量)以外的所有影响实验结果的变量,这些变量不是本实验所要研究的变量,所以又称无关变量、无关因子、非实验因素或非实验因子。
【解答】AC、由四套装置图可知,在定滑轮的两侧各安装一个弹簧测力计,然后分别测量出钩码的重力和拉力;测量钩码重力的弹簧测力计应上方固定,所以AC不符合题意;
BD、为了控制变量,所以弹簧测力计应都是固定上方,下方可动,故B错误;D正确;
故答案为:D。
14.【答案】 C
【解析】【分析】根据图片可知,这座桥是左右对称的。根据二力平衡的原理计算出顶层砖块对右侧中间层砖块的压力。当中间层的砖块要向左倾倒而未倒时相当于一个杠杆,支点就是最下层砖块的左上顶点,此时阻力就是中间层砖块的重力G,作用在它的中心;动力就是顶层砖块的压力,根据杠杆的平衡条件计算出右侧中间层砖块跨出的长度,最后根据桥的最大跨度=底层砖块长+中间层跨出长度×2计算即可。
【解答】如图,顶层砖对两侧砖的压力F为砖重力的一半,即F=G/2。以中间层右侧的砖为研究对象,以最下层砖块的左上顶点为支点,假设砖块的右侧离与下层砖块的左上顶点(支点)的距离为x,则顶层右侧砖给予中间层右侧的砖块压力的力臂为x,中间层右侧的砖受到的阻力(即为其自身的重力)的力臂为(12cm-x),根据应用杠杄平衡条件有:G/2×x=G×(12cm-x),解得x=8cm ,可推知此时该砖恰好能平衡砖的最大跨度=24cm+2×8cm=40cm。
故答案为:C
15.【答案】 A
【解析】【分析】掌握杠杆的五个要素:支点、动力、阻力、动力臂、阻力臂。根据动力和阻力画出动力臂和阻力臂;注意力臂是一条线段,而非直线。(1)支点是杠杆绕着转动的固定点,动力和阻力都是外界作用在杠杆上的力,都是杠杆受到的力.力臂是支点到力的作用线的垂直距离。(2)画力臂的方法:首先确定支点;然后找到动力和阻力,并用虚线延长动力和阻力的作用线;然后由支点向力的作用线引垂线,支点到垂足的距离就是力臂。
【解答】支点是杠杆绕着转动的固定点,动力和阻力都是外界作用在杠杆上的力,都是杠杆受到的力,分析可知O是支点,动力F1作用N点,阻力F2作用在M点;N点向下施力,M点受力方向向上,
故选A
二、填空题
16.【答案】 (1)1.4
(2)21;热传递
【解析】【分析】(1)首先根据s=nh计算出拉力移动的距离,再根据W总=Fs计算出拉力做的总功,最后根据W有=W总η计算克服物体A重力做的功;
(2)酒精燃烧放出的热量与水吸收的热量相同,首先根据Q=cm△t计算出水吸收的热量,再根据m酒=Q酒q酒计算需要燃烧酒精的质量。改变内能的两种方式:①做功;②热传递。
【解答】(1)拉力移动的距离据s=nh=0.1m×2=0.2m;
拉力做的总功W总=Fs=10N×0.2m=2J;
克服物体A重力做的功W有=W总η=2J×70%=1.4J。
(2)水吸收的热量为:Q=cm△t=4.2×103J/(kg?℃)×2kg×(100℃-25℃)=6.3×105J;
要燃烧酒精的质量m酒=Q酒q酒=6.3×105J3.0×107J/kg=0.021kg=21g。
上述过程中,水的内能增加是通过热传递的途径实现的。
17.【答案】 (1)改变力的方向
(2)省力
【解析】【分析】(1)定滑轮的作用是改变拉力的方向,而不能省力;
(2)比较动力臂和阻力臂的大小,然后对杠杆进行分类。
【解答】(1)根据乙图可知,如果不使用定滑轮,那么拉力的方向应该向上,使用定滑轮后拉力的方向变为向下,因此定滑轮的作用是:改变力的方向;
(2)如下图所示:
因为动力臂大于阻力臂,所以该状态下的桶盖属于省力杠杆。
18.【答案】 (1)4.8
(2)B
【解析】【分析】(1)动滑轮可以省一半的力,据此根据弹簧测力计的示数可确定物体的重;(2)根据杠杆的平衡条件,在阻力一定的情况下,减小阻力臂可以省力.本题主要考查了对动滑轮和杠杆的应用,理解各自的工作特点,是正确解答的关键.
【解答】解:(1)图中弹簧测力计的分度值为0.2N,其示数为2.4N;在不计摩擦及滑轮和绳子的自重的情况下,动滑轮可以省一半的力.
故物体的重力G=2F=2×2.4N=4.8N;(2)剪刀在使用时相当于杠杆,根据杠杆的平衡条件,阻力不变,动力臂不变,将被剪物体应放在B点时,阻力臂更小,所以更省力.
故答案为:(1)4.8;(2)B.
19.【答案】 动力臂大于阻力臂;
【解析】【分析】(1)根据杠杆的平衡条件可知,如果动力臂大于阻力臂,那么为省力杠杆;如果动力臂小于阻力臂,那么为费力杠杆;如果二者相同,那么为等臂杠杆,不省力也不费力;
(2)首先判断开瓶器对瓶盖的作用力方向,然后根据相互作用力原理判断阻力的方向。
【解答】(1)开瓶器的在瓶盖上的部分是支点,动力作用在末端,而阻力作用在瓶盖下边,因为动力臂大于阻力臂,所以它能省力;
(2)当作用在开瓶器最右端的手向上用力时,咬合在瓶盖下面的牙对瓶盖的作用力向上;根据相互作用力原理可知,开瓶器上的阻力与它方向相反,即向下,如图:
20.【答案】 (1)60
(2)90
(3)10~90
【解析】【分析】杠杆原理 亦称“杠杆平衡条件”。要使杠杆平衡,作用在杠杆上的两个力(动力和阻力)的大小跟它们的力臂成反比。动力×动力臂=阻力×阻力臂。
【解答】(1)若 G=30 牛,以木棒为研究对象,木棒受力平衡,故木棒受台面的支持力为60N, 台面收到木棒的压力与木棒受到台面的支持力为相互作用力,即为60N;
(2)若要使木棒右端下沉,则B点为支点,根据杠杆平衡条件GB×0.3=GA×0.9, 解得GB=90N,即B端挂的物体至少要大于90牛;
(3)若 B 端挂物体后,木棒仍在水平台面上静止,以A点为支点,根据杠杆平衡条件GB ×0.9=GA×0.3,解得则 GB=10N, 即G 的取值范围为.:10~90牛。
故答案为:(1)60;(2)90;(3)10~90。
21.【答案】 (1)4
(2)C
【解析】【分析】(1)杠杆平衡时动力×动力臂=阻力×阻力臂,可用公式F1· L1=F2·L2计算出G2;(2)力臂OB折过一定角度后其余都不变,要使杠杆继续平衡必须使G2的力臂长度与原来相同就行。
【解答】(1)G1·LAO =G2· LBO? 2N×0.2m=G2×0.1m? G2=4N;(2)由乙图可知当将G2移动到②点处时力臂与原来相等,所以当G2移动到②处时杠杆继续保持平衡。
故答案为:1、4N;2、C
22.【答案】 20;60;540
【解析】【分析】(1)根据杠杆平衡条件求出拉力的大小; (2)肩对木棒的支持力大小为F=FA+FB; (3)对人进行受力分析即可解答。
【解答】解: (1)由题根据杠杆的平衡条件有:F×OB=G×OA, 即:F×(0.6m﹣0.2m)=40N×0.2m, 所以:F=20N;即手压木棒的压力大小为20N;
(2) 肩对木棒的支持力大小为F′=F+G=20N+40N=60N;
(3)以人为整体,人处于静止状态,受到人、物体的重力和地面对人体的支持力是一对平衡力,大小相等,即F支=G人+G物=mg+G物=50kg×10N/kg+40N=540N。
又因为人对地面的压力大小和地面对人体的支持力是一对相互作用力,大小相等,即F压=F支=540N
故答案为:20;60;540。
三、实验探究题
23.【答案】 (1)大
(2)将八个风力板的迎风面朝南放置
(3)每天结束时,以倾倒风力板中记录风力最大的作当天最强风力
【解析】【分析】此时的风力板构成了一个杠杆,动力时风力,阻力是重力。
【解析】(1)风力板受风力和重力作用,所以,当风力为动力时,重力则为阻力,风力板越重越不容易倾倒。所以压重板上的铁板越重,风力板倾倒时记录的风力越大 。
(2)在开阔的水平地面放置风力探测仪时,要使风力探测仪面向风吹来的方向,因为在南风盛行的地方,所以小明应将八个风力板的迎风面朝南放置。
(3) 每天结束时,以倾倒风力板中记录风力最大的作当天最强风力。
故答案为:(1)大;(2) 将八个风力板的迎风面朝南放置 ;(3) 每天结束时,以倾倒风力板中记录风力最大的作当天最强风力
四、解答题
24.【答案】 (1)定滑轮
(2)减小摩擦
(3)W=Fs=Gh=20牛×1.5米=30焦
(4)晾衣杆可看作是一个杠杆,左侧绳与晾衣杆的交点为杠杆的支点,l2为悬挂点到支点的距离
根据杠杆平衡公式:F1×l1=F2×l2
可得l2= F1×l1F2 = 15牛×20厘米×1020牛 =150厘米
挂在9、10、11三个孔上晾晒会损坏晾衣架。
【解析】【分析】(1)根据这个简单机械的工作特点推断它的种类;
(2)减小摩擦的方法:①减小压力;②减小接触面的粗糙程度;③改变接触面;③添加润滑剂;
(3)根据W=Gh计算对衣服做的功;
(4)可以将晾衣杆看作一个杠杆,左侧绳子与晾衣杆的交点为支点,衣服的重力为阻力,衣服的悬挂点到支点的距离为阻力臂;右侧绳子的拉力为动力,动力臂就是晾衣杆的长度,根据杠杆的平衡条件,计算出阻力臂的长度,然后对小孔的位置进行定位,从而确定钢丝绳会断裂的小孔位置。
【解答】(1)根据图片可知,安装在天花板内的机械,应该能够旋转,并且它的位置固定不变,因此应该是定滑轮。
(2)使用一段时间后,对手摇器的转轴添加润滑剂,目的是减小摩擦。
(3)至少对衣服做功:W=Fs=Gh=20N×1.5m=30J;
(4)晾衣杆可看作是一个杠杆,左侧绳与晾衣杆的交点为杠杆的支点,l2为悬挂点到支点的距离;
根据杠杆平衡公式:F1×l1=F2×l2;
可得:?l2= F1×l1F2=15N×20cm×1020N=150cm;??
那么可以悬挂的最右边的孔为:150cm20cm+1≈8;
因此挂在9、10、11三个孔上晾晒会损坏晾衣架。
25.【答案】 (1)解:s=2×2米=4米
W=Fs=18牛×4米=72焦
(2)解: P=Wt=72J4s=18W
(3)解:f=0.35G=0.35×100牛=35牛
G轮=2F-f=2×18N-35N=1N
【解析】【分析】该题主要考查滑轮组的相关计算,并综合考查了功率和做功的计算;
【解答】(1)滑轮组省力费距离,由可知动滑轮上的绳子段数n,而绳子自由端移动的距离是物体移动的n倍;所以绳子自由端移动的距离为S=2×2m=4m;W=FS=18N×4m=72J;故答案为:S=2×2m=4m;W=FS=18N×4m=72J;(2)功率是做功与时间的比值,而由题可知W=72J;t=4s;所以 P=Wt=72J4s=18W ;故答案为: P=Wt=72J4s=18W ;(3)人通过滑轮组拉动物体匀速运动,说明处于平衡状态;所以动力等于阻力;阻力包括物体受到的摩擦力、滑轮的重力两部分;而滑轮组省力的,则拉力的n倍等于阻力;f=0.35G=0.35×100牛=35牛; G轮=2F-f=2×18N-35N=1N ;故答案为:f=0.35G=0.35×100牛=35牛; G轮=2F-f=2×18N-35N=1N ;
故答案为:(1)S=2×2m=4m;W=FS=18N×4m=72J;(2) P=Wt=72J4s=18W ;(3)f=0.35G=0.35×100牛=35牛; G轮=2F-f=2×18N-35N=1N 。
26.【答案】 (1)解:物体的重力为:G=mg=100kg×10N/kg=1000N;
动滑轮的重力为:G轮=m轮g=8kg×10N/kg=80N;
则拉力为:F= 1n (G+G轮)= 12 ×(1000N+80N)=540N;
答:拉力的大小为540N;
(2)拉力移动的距离为s=2h=2×3m=6m;
拉力做的功为:W=Fs=540N×6m=3240J;
拉力的功率为:P= Wt = 3240J30s =108W.
答:这段时间内人拉绳子做功的功率为108W.
【解析】【分析】(1)根据公式F= 1n (G+G轮)求出拉力;(2)根据功和功率的计算公式解答.
27.【答案】 (1)V排=V金=Sh=0.05m2×0.2m=0.01m3
F浮=ρ水V排g=1.0×103kg/m3×10N/kg×0.01m3=100N
(2)从重物上表面刚露出水面到其下表面刚离开水面,用时t2=4s:上升高度为物体的高h=0.2m,得上升速度v===0.05m/s;
第一阶段上升高度s=vt1=0.05m/s×40s=2m
绳对重物做的功W=F1s=140N×2m=280J
(3)第一阶段中,此时拉力的大小F=13(140N+60N)=2003牛 , 此时的机械效率η=W有用W总=F绳hF人×3h×100%=140牛×h200牛3×3h×100%≈70%第三阶段中,此时绳子给予物体的拉力的大小等于物体的重力,由物体第一阶段在水中受到的浮力和绳子给予物体的拉力可得G物=100牛+140牛=240牛,拉力的大小F=13(240N+60N)=100牛,此时的机械效率
【解析】【分析】(1) 在第一阶段运动中,V排就是物体的体积,在利用阿基米德原理进行计算即可。
(2)因为重物一直做竖直向上的匀速直线运动,所以第一阶段和第二阶段的速度是一样的。利用第二阶段的路程和时间求出物体移动的速度,从而求出第一阶段物体通过的路程,最后用公式W=Fs求出所做的功。
(3)机械效率等于有用功除以总功;在此滑轮组中, F人=13(F物+G动),s=3h。人拉绳子所做的是总功,人克服物体和动滑轮的阻力所做的功是有用功。
28.【答案】 (1)有用功:W有用=Gh=5N×0.3m=1.5J;
总功:W总=Fs=4N×0.5m=2J,
机械效率:η= W有用W总 ×100%= 1.5J2J ×100%=75%;
答:机械效率η1为75%
(2)变小;
钩码的悬挂点在A点时,由于杠杆的重力会阻碍杠杆转动,
则由杠杠的平衡条件得:G?OA+G杠杆? 12 OC=F?OC;
悬挂点移至B点时,由杠杠的平衡条件得G?OB+G杠杆? 12 OC=F′?OC,
观察比较可知,悬挂点移至B点时,OB<OA,即钩码重力的力臂变小,所以拉力F也变小;
杠杆的机械效率:η= W有用W总 ?= W有用W有用+W额 ?= 11+W额W有用 ;
因为杠杆升高的高度不变,所以克服杠杆自重所做的额外功不变(即W额=G杠杆?h杠杆不变);由于悬挂点B更接近支点,所以钩码提升的高度减小,根据W有用=Gh可知,有用功减小;
从上面η的表达式可知:W有用减小、W额不变,所以 W额W有用 变大,分母变大,η就减小;即η2<η1 .
【解析】【分析】(1)根据W=Gh求出有用功;根据W=Fs求出总功,根据η= W有用W总 求出机械效率;(2)将钩码的悬挂点从A点移至B点,改变了钩码重力的力臂,根据杠杆平衡条件分析,改变了弹簧测力计的拉力,改变了弹簧测力计的拉力做功的多少,改变了机械效率的高低.本题考查的是学生对有用功、总功、额外功、机械效率计算公式的理解和掌握,同时还考查杠杠平衡条件的应用.
29.【答案】 (1)根据杠杆平衡条件:F1l1=F2l2 , 得m1gl1=m2gl2 , 即:m1l1=m2l2 , 2kg×5cm=m2×10cm,得m2=1kg
(2)2;4
(3)<
【解析】【分析】(1)将O点看作杠杆的支点,秤砣的重力看做阻力,OB为阻力臂;物体的重力为动力,动力臂为OA,根据杠杆的平衡条件计算即可;
(2)根据此时物体的质量确定B处标的刻度值。再次根据杠杆的平衡条件计算此时物体的质量即可;
(3)秤砣的重力相当于阻力,根据杠杆的平衡条件分析阻力臂的长度变化即可。
【解答】(1)将O点看作杠杆的支点,秤砣的重力看做阻力,OB为阻力臂;物体的重力为动力,动力臂为OA,
根据杠杆平衡条件:F1l1=F2l2,
即:m1gl1=m2gl2,
m1OA=m2OB;
2kg×5cm=m2×10cm;
解得:m2=1kg?。
(2)因为秤砣在B处平衡时,物体的质量为2kg,所以小金在B处标的刻度应为2kg;
若图中OC=2OB,
根据杠杆的平衡条件得到:G物×OA=G秤砣×OC;
m物g×OA=m秤砣g×OC;
m物×OA=m秤砣×OC;
m物×5cm=1kg×20cm;
解得:m物=4kg;
因此在C处的刻度应为4kg;
(3)根据杠杆的平衡条件得到:
G物×OA=G秤砣×OC';
m物×OA=m秤砣×OC';
当物体的质量m物 , OA不变时,秤砣的质量m秤砣增大,那么阻力臂OC'变小,
因此其读数<2kg。
30.【答案】 (1)解:∵杠杆平衡时有:F1×L1=F2×L2
∴m1g×L1=m2g×L2
变形得到:L1:L2=m2:m1
(2)仍然平衡;
以浸没于水的物体为研究对象进行受力分析:
F拉+F浮=m物g
F拉=m物g-F浮=m物g-ρ水gV物=(1- ρ水ρ物 )m物g
所以;F拉1×L1=(1- ρ水ρ物 )m1gL1
F2×L2=(1- ρ水ρ物 )m2gL2
∵m1gL1=m2gL2
∴F拉1L1=F拉2L2
因此杠杆仍然平衡
【解析】【分析】(1)将左边的物体重力看作动力,右边的物体重力看作阻力,根据杠杆的平衡条件列出平衡关系式,借助数学运算得到左右悬挂点到支点O的距离L 1与L 2之比;
(2)当两个物体浸没在水中时,它们都会受到浮力,根据二力平衡条件得到: F拉+F浮=m物g 。据此计算出它们作用在杠杆上的拉力F拉1和F拉2;接下来分别计算杠杆两边动力和动力臂的乘积以及阻力和阻力臂的乘积,借助(1)中的结果对它们的大小进行比较即可。
31.【答案】 (1)铜环
(2)
(3)当配重柄水平时,可求出配重的最小质量,杠杆示意图如图2:
OD= 12 ×OC= 12 ×1.4cm=1cm,根据杠杆的平衡条件:
G1l1=G2l2 , m1gl1=m2gl2 , m2=m1 m1ODOB = 4g×1cm1cm =4g;
当小壶盖水平时,可求出配重的最大质量,杠杆示意图如图3:
OE= 12 ×OB= 12 ×1cm=0.71cm,
根据杠杆的平衡条件:
G1l1′=G2l2′,m1gl1′=m2gl2′,
m2′=m1 OCOE = 4g×1.4cm0.71cm ≈7.89g。
【解析】【分析】(1)外壳是金属,应该与火线、零线绝缘,根据已知条件分析。
(2)重力G方向竖直向下,根据力臂的定义做出重力的力臂;
(3)根据杠杠的平衡条件,当配重柄水平时,配重的质量最小;当水壶盖水平时,配重的质量最大,利用数学知识结合杠杆的平衡条件求解。
【解答】(1)铜是导体,由题意,铜环①、铜环②之间是绝缘的,说明之间有底盘的绝缘体;②、③之间常温下有十几欧姆的电阻,为加热电阻,故与水壶金属外壳相连的装置只能是铜环①,否则与②或③相连则有触电的危险。
(2)水壶盖的重力G方向竖直向下,根据力臂的定义做出重力的力臂,如下图1所示:
(3)当配重柄水平时,可求出配重的最小质量,杠杆示意图如图2:
OD=12×OC=12×1.4cm=1cm , 根据杠杆平衡条件可得:G1l1=G2l2 , 即m1gl1=m2gl2 , m,2=m1=m1ODOB=4g×1cm1cm=4g;
当壶盖水平时,可求出配重的最大质量,杠杆示意图如图3:
OE=12×OB=12×1cm=0.71cm , 根据杠杆平衡条件可得:G1l'1=G2l'2 , m1gl'1=m2gl'2 , m,2=m1=m1OCOE=4g×1.4cm0.71cm=7.89g
故答案为:(1)铜环①;(2)如图1所示;(3)配重B的质量取值范围4g---7.89g
32.【答案】 (1)20
(2)l1
(3)列车每秒钟做功5152千焦;1.55×105N
【解析】【分析】力的作用线到转动轴的垂直距离。与动力对应的力臂叫动力臂,与阻力对应的力臂叫阻力臂。功率是指物体在单位时间内所做的功的多少,即功率是描述做功快慢的物理量。功的数量一定,时间越短,功率值就越大。求功率的公式为功率=功/时间。
【解答】(1) t=SV=40km120km/h=13h=13×60min=20min ;故答案为:20;(2)力臂是支点到力的垂直距离,图中的杠杆O是支点,要找O点到F的垂直线段即可;故答案为:l1;(3)功率是用来表示物体做功快慢的物理量,所以5152千瓦表示牵引力每秒做功5152kJ;∵P= Wt=F?st =F·v?? v=120km/h=33.33m/s
∴F= Pv=5152×103W33.33m/s =1.55×105N??? f=F=1.55×105N;故答案为:1.55×105N;
故答案为:(1)20;(2)l1;(3)列车每秒钟做功5152千焦;1.55×105N。
33.【答案】 (1)电动机对零件做的功:
W=gh=mgh=600kg×10N/kg×4m=2.4×104J,
因横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计,
所以,拉力做的功即为克服零件重力所做的功,
则电动机对零件做功的功率:
P=Wt=ght=mght =mgv=600kg×10N/kg×0.4m/s=2.4×103W,
则电动机的最小功率为2.4×103W;
(2)mg-mgvLt
【解析】【分析】(1)知道零件的质量和提升的高度,根据W=Gh=mgh求出电动机对零件做的功,横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计,拉力做的功即为克服零件重力所做的功,根据P= Wt = Ght = mght =mgv求出电动机对零件做功的功率即为电动机的最小功率;(2)横梁对轨道A的压力F和轨道对横梁的支持力是一对相互作用力,根据v= st 可得AD段的长度,从而得出轨道对横梁的支持力和重物的力臂,根据杠杆的平衡条件得出等式即可求出轨道对横梁的支持力与t的关系,再根据相互作用力的关系得出得出答案.本题考查了功和功率的计算以及速度公式、杠杆平衡条件的应用,利用相互作用力的条件把横梁对轨道A的压力F转化为轨道对横梁的支持力来处理是关键.
【解答】解:(1)电动机对零件做的功:
W=Gh=mgh=600kg×10N/kg×4m=2.4×104J,
因横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计,
所以,拉力做的功即为克服零件重力所做的功,
则电动机对零件做功的功率:
P= Wt = Ght = mght =mgv=600kg×10N/kg×0.4m/s=2.4×103W,
则电动机的最小功率为2.4×103W;(2)横梁对轨道A的压力F和轨道对横梁的支持力是一对相互作用力,
把MN看作一根杠杆,B为支点,A端对横梁的支持力为动力,零件的重力为阻力(其它重力和摩擦力不计);
由v= st 可得,t时间内AD段的长度:LAD=vt,
则零件重力的力臂:LG=L﹣LAD=L﹣vt,
轨道A对横梁支持力的力臂为L,
由杠杆的平衡条件可得:F支持?L=G?(L﹣vt),
则F支持= G·(L-vt)L =G﹣ GvtL =mg﹣ mgvL t,
由相互作用力的特点可知,横梁对轨道A的压力F与时间t的关系式:
F=F支持=mg﹣ mgvL t.
答:(1)电动机对零件做的功为2.4×104J,电动机的功率至少为2.4×103W;(2)mg﹣ mgvL t.
34.【答案】 (1)15;FC=FD
(2)②
【解析】【分析】(1)根据杠杆平衡条件计算作用在B点竖直向下的力FB的大小;通过比较FC、FD两个力的力臂与FB的力臂的关系,根据杠杆平衡条件分析FC、FD大小关系;(2)流体的压强跟流速有关,流速越大,压强越小.此题考查杠杆平衡条件的应用、流体压强和流速的关系,难点在(1),关键是从图示中得出FC、FD两个力的力臂均与FB的力臂相等,然后利用杠杆平衡条件分析解答.
【解答】解:(1)根据杠杆平衡条件可得:G×OA=FB×OB,
OA=3OB=0.6m,则OB=0.2m,
所以,作用在B点竖直向下的力FB= = =15N;
由图可知,FC、FD两个力的力臂均与FB的力臂相等,都是圆的半径,阻力和阻力臂不变,
撤去FB后,按图示方向分别施加FC、FD两个力,且毎次都使杠杆在水平位置平衡,
根据杠杆平衡条件可知,FC、FD大小关系为FC=FD;(2)由图可知B的下端注射器的横截面积大,A的下端注射器的横截面积小,快速向内推动活塞,B的下端空气流速小,压强大,A的下端空气流速大,压强小,所以,
在此过程中可现察到A、B两孔处气球的鼓起情况是B孔处气球大.
故答案为:(1)15;(2)FC=FD;(2)②.
35.【答案】 (1)大
(2)改变力的方向;6000
(3)由于水平移动时,重力方向上没移动距离,故水平移动过程中重力没做功;
W=Fs=Gh=1.2×104N×30m=3.6×105J,
答:此过程中克服货物重力做功3.6×105J;
(4)有用功W有用=Gh=1.2×104牛×30米=3.6×105焦,
总功W总= W有用η = 3.6×105J90% ?=4×105焦,
实际功率P= W总t = 4×105J50s ?=8000W.
答:该起升电动机的实际功率是8000瓦.
【解析】【分析】(1)因动力臂及动力的乘积不变,则由杠杆的平衡条件可知配重与配重臂的关系;(2)根据滑轮的特点分析其作用;根据滑轮组特点确定绳子段数求出物体重力;再结合重力公式求出质量;(3)根据功的公式W=Fs求出克服重力做功大小;(4)求出有用功,利用效率公式求总功,再利用P= Wt 求实际功率.
【解答】解:(1)由杠杆的平衡条件F1L1=F2L2(动力×动力臂=阻力×阻力臂)可得:F2= F1L1L2 ,由此可知当阻力臂和动力不变时,阻力与动力臂成正比;即动力臂越大,阻力越大;动力臂越小,阻力越小.故为保持平衡,起重臂的长度越长的塔式起重机,配备的平衡重的质量应越大;(2)图示中滑轮a为定滑轮,其作用是改变用力的方向;
由题意可知该滑轮组承担总重的绳子有2段,故G=2F=3×104牛×2=6×104牛
由G=mg可得:m= Gg=6×104N10N/kg ?=6000千克;
浙江省2016-2020年科学中考(物理)试题分类(7)——简单机械
一、单选题
1.(2019·嘉兴)为便于研究,某健身器材中训练拉力部分的机械结构可简化为如图所示的滑轮组。若不计摩擦,下列有关分析正确的是(?? )
A.?两个滑轮在装置中起的作用相同
B.?拉力移动的距离与配重上升的距离相同
C.?沿方向1与2匀速拉动配重,所用的力大小相等
D.?将配重提升相同高度,用该装置与直接提升所做的功相等
2.(2018·宁波)如图所示,F1=4N,F2=3N,此时物体A对于地面静止,物体B以0.1m/s的速度在物体A表面向左做匀速直线运动(不计弹簧测力计、滑轮和绳子的自重及滑轮和绳子之间的摩擦)。下列说法错误的是( ???)
A.?F2的功率为0.6W????????????????????????????????????????????????B.?弹簧测力计读数为9N
C.?物体A和地面之间有摩擦力?????????????????????????????????D.?如果增大F2 , 物体A可能向左运动
3.(2020·宁波)现有一根形变不计、长为L的铁条AB和两根横截面积相同、长度分别为La、Lb的铝条a、b。将铝条a叠在铁条AB上,并使它们的右端对齐,然后把它们放置在三角形支架O上,AB水平平衡,此时OB的距离恰好为La , 如图所示。取下铝条a后,将铝条b按上述操作方法使铁条AB再次水平平衡,此时OB的距离为Lx。下列判断正确的是( ?)
A.?若La
C.?若Lb
A.?滑轮组中A滑轮用于改变力的方向???????????????????????B.?当C杆伸长时吊臂对D杆的压力将变大
C.?当D杆伸长时力F的力臂将变小????????????????????????????D.?H的作用是工作时以防翻车和避免轮胎受到的压力过大
5.(2017·台州)小柯用图中提升重为400牛的物体,不计摩擦和滑轮自重,下列说法正确的是(? )
A.?两个滑轮均为定滑轮???????????????????????????????????????????B.?人将绳子拉过1米,物体也上升1米
C.?物体匀速上升时,人对绳子的拉力为200牛?????????D.?使用该装置不能省力,但能改变力的方向
6.(2017·杭州)如图所示装置,在水平拉力F的作用下,物体M沿水平地面做匀速直线运动,已知弹簧秤读数为10牛,物体M的运动速度为1米/秒(若不计滑轮与绳子质量、绳子与滑轮间的摩擦、滑轮与轴间的摩擦)。那么在此过程中(?? )
A.?物体M与地面间的摩擦力为5牛???????????????????????????B.?物体M与地面间的摩擦力为10牛
C.?水平拉力F做功的功率为20瓦??????????????????????????????D.?1秒内滑轮对物体M做功为10焦
7.(2017·宁波)如图所示,用同一个动滑轮先后提升同一物体,使物体以相同速度匀速上升相同的高度,所用的力分别是F甲和F乙 , 拉力做功的功率分别是P甲和P乙。若不计摩擦、动油轮重和绳重,则F甲与F乙、P甲与P乙之间的大小关系是( )
A.?F甲
C.?F甲>F乙? P甲=P乙???????? ??????????????????????????????????????D.?F甲
A.?????????????B.?????????????C.?????????????D.?
9.(2016·缙云)如图,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块Q相连,从滑轮到P和到Q的两段绳都是水平的。已知Q与P之间以及P与桌面之间的动摩擦因数都是μ,两物块的质量都是m,滑轮的质量、滑轮轴上的摩擦都不计。已知滑动摩擦力f与压力F压之间的关系为f=μF压,若用一水平向右的力F拉着P使它做匀速运动,则F的大小为(???? )
A.?4μmg??????????????????????????????????B.?3μmg??????????????????????????????????C.?2μmg??????????????????????????????????D.?μmg
10.(2016·缙云)为模拟盘山公路,现将连接了重1N小球的细线穿入一根长1m的细管。如图,将细管从竖直放置的圆柱体底部a点开始斜向上缠绕5圈后,恰好绕至顶部b点,相邻细管间的高度均为12cm。在b点处通过细线用0.8N的拉力(与管的轴线平行)将管口的小球从a点匀速拉至b点。则缠绕在圆柱体上的细管(模拟的盘山公路)的机械效率为(???? )
A.?83.3%????????????????????????????????????B.?80%????????????????????????????????????C.?75%????????????????????????????????????D.?60%
11.(2017·丽水)如图所示,使用时属于费力杠杆的是(??? )
A.?镊子夹石块????????????B.?起子开瓶盖????????????C.?羊角锤拔铁钉????????????D.?天平称物体质量
12.(2017·嘉兴)如图是一种切甘蔗用的铡刀示意图。下列有关说法正确的是(?? )
A.?刀刃很薄可以增大压力???????????????????????????????????????B.?铡刀实质上是一种费力杠杆
C.?甘蔗放在a点比b点更易被切断????????????????????????????D.?手沿F1方向用力比沿F2方向更省力
13.(2020·绍兴)如图,甲、乙实验可以得出“定滑轮不能省力”这一结论,小敏想通过一次实验既得出结论,又能直接显示出钩码的重力大小,于是在左侧加上一个相同的弹簧测力计(弹簧测力计重力不能忽略、绳和滑轮之间摩擦不计),下列四套装置中能实现的是( ???)
A.????????B.?????????????????C.??????????????????????????????D.?
14.(2016·缙云)由五块相同的红砖块构成的桥,如图所示,已知红砖的尺寸是240×115×53(单位:毫米),则此桥的最大跨度L为(???? )
A.?24厘米???????????????????????????????B.?36厘米???????????????????????????????C.?40厘米???????????????????????????????D.?48厘米
15.(2017·温州)小明在按压式订书机的N点施加压力,将订书针钉入M点下方的纸张中,能正确表示他使用该订书机时的杠杆示意图是(? )
A.?????????????????B.?????????????????C.?????????????????D.?
二、填空题
16.(2020·宁波)科学上通常用“功”和“热量”来量度物体能量的变化。
(1)在“使用动滑轮”活动中,小科利用如图所示装置,用竖直向上的大小为10N的拉力F使物体A匀速提升了0.1m。如果该装置的机械效率为70%,则这一过程中,克服物体A的重力所做的功为________J,这个值也是物体A增加的机械能。
(2)把质量为2kg,温度为25℃的水加热到100C,至少需要完全燃烧________g的酒精。上述过程中,水的内能增加是通过________(填“做功”或“热传递”)的途径实现的。【已知:水的比热容为4.2×103J/(kg℃),酒精的热值为3.0×107J/kg】
17.(2020·金华·丽水)简单机械广泛应用于日常生活。某小区物业为了方便住户扔垃圾,对垃圾桶进行了简易改装(如图甲)。被拉起的垃圾桶盖可看成是一个简易杠杆。图乙为桶盖与绳子成90°角且处于静止状态时的示意图,O为杠杆支点,A为绳子拉力F的作用点,B为桶盖的重心。根据图乙回答下列问题:
(1)定滑轮的作用是________;
(2)该状态下的桶盖属于________(填“省力”、“费力”或“等臂”)杠杆。
18.(2016·金华)简单机械在我们的生活中应用广泛,请回答下列有关简单机械的问题:
(1)如图甲,物体处于静止状态,物体的重力是________N(不计摩擦及滑轮和绳子的自重).
(2)如图乙是一把剪刀,在使用过程中要达到相对省力的效果,则被剪物体应放在________点(填字母“A”或“B”).
19.(2019·湖州)生活中我们常用开瓶器打开瓶盖,如图所示使用开瓶器能省力的原因是________?。请在答题卷的图中画出作用在开瓶器上的阻力________。
20.(2018·杭州)如图所示,将长为 1.2 米的轻质木棒平放在水平方形台面上,左右两端点分别为A、B,它们距台面边缘处的距离均为 0.3 米。在 A 端挂一个重为 30 牛的物体,在 B 端挂一个重为 G 的物体。
(1)若 G=30 牛,台面收到木棒的压力为________牛。
(2)若要使木棒右端下沉,B 端挂的物体至少要大于________牛。
(3)若 B 端挂物体后,木棒仍在水平台面上静止,则 G 的取值范围为________牛。
21.(2017·衢州)如图为小柯制作的“杠杆力臂演示仪”,杠杆AOB可绕O点(螺母)转动,OA=0.2m,OB=0.1m,G1=2N,杠杆自身重力和摩擦不计,固定装置未画出。
(1)当杠杆处于甲图所示水平位置平衡时,G2的重力为________N。
(2)松开螺母保持OA不动,使OB向下折一个角度后,再拧紧螺母形成一根可绕O点转动的杠杆AOB'? (B'点对应B点),保持G1位置不变,要使杠杆在图乙位置保持平衡,则G2应该移动到__________。
A.B’点处
B.① 点处
C.②点处
D.③点处
22.(2017·杭州)小金将长为0.6米、质量可忽略不计的木棒搁在肩上,棒的后端A挂一个40牛的物体,肩上支点O离后端A为0.2米,他用手压住前端B使木棒保持水平平衡,如图所示。小金的质量为50千克,则此时手压木棒的力大小为________牛,肩对木棒的支持力大小为________牛,人对地面的压力大小为________牛(g=10牛/千克)。
三、实验探究题(共1题;共3分)
23.(2016·缙云)如图所示为小明自制的风力板,a板为迎风板,其迎风面承受风力,b板为压重板,它水平放置,m为压重板上的铁板(a、b板重力不计)。当压重板上铁板重力一定时,风力大到一定程度,风力板就会倾倒。小明通过查阅资料和实验,在压重板上加上重力不同的铁板,制成能测风力1~8级的8个风力板,构成一套风力探测仪。在南风盛行的某地,小明用这套风力探测仪测定当天最强的风力。
(1)压重板上的铁板越重,风力板倾倒时记录的风力越________。
(2)在开阔地的水平地面放置风力探测仪时,小明应________。
(3)小明确定当天最强风力的方法是________。
四、解答题
24.(2020·台州)晾衣架(如图)给日常生活带来许多方便,转动手摇器能使横杆上升或下降
(1)安装在天花板上虚线框内的简单机械应是________。
(2)使用一段时间后,对手摇器的转轴添加润滑剂,目的是________。
(3)将挂在晾衣架上重为20牛的衣服升高1.5米,至少对衣服做多少功?
(4)由于使用不当.造成晾衣架右侧钢丝绳受损,最多只能承受15牛的力,左侧钢丝绳能正常使用。晾衣架的横杆上有11个小孔,相邻两孔间的距离均为20厘米。现准备将重为20牛的一件衣服挂到水平横杆的小孔进行晾晒,通过计算说明挂在哪些编号的小孔,在侧钢丝绳会断裂(横杆、衣架和钢丝绳等自重不计)。
25.(2018·湖州)在拓展课上,小泉同学模拟某建筑工地上拉动工件的情景,设置了如图所示的滑轮组。他用该滑轮组在4秒内将一个重为100牛的物体,沿着水平地面匀速拉动了2米。人的拉力为18牛,物体移动时受到地面的摩擦力为物重的0.35倍,不计绳重及机械的摩擦。求:
(1)人的拉力所做的功。
(2)人的拉力做功的功率。
(3)动滑轮受到的重力。
26.(2017·湖州)建筑工人利用如图所示装置,将质量为100千克的沙袋从地面匀速提到3米高的一楼楼面,用时30秒.已知动滑轮的质量为8千克,不计绳子重力和摩擦.
求:
(1)拉力的大小.
(2)这段时间内人拉绳子做功的功率.
27.(2016·缙云)某同学为了体验“南海一号”的打捞过程,特利用滑轮组从水下打捞一重物.如图所示,用一个底面积S=0.05m2 , 高h=0.2m的长方体形状的重物模拟“南海一号”,该同学站在岸边拉动绳子的自由端,使重物从水底开始向上运动.假定重物一直做竖直向上的匀速直线运动,并经历三个运动阶段:第一阶段,从重物在水底开始运动到重物的上表面刚露出水面,绳对重物的拉力F1=140N,用时t1=40s;第二阶段,从重物上表面刚露出水面到其下表面刚离开水面,用时t2=4s;第三阶段,从重物下表面离开水面后在空中上升。已知动滑轮所受重力G=60N,ρ水=1.0×103kg/m3 , g=10N/kg,不计绳重、轮与轴之间的摩擦及水的阻力,不考虑重物出水前后质量的变化.求:
(1)在第一阶段运动中,水对重物的浮力F浮为多大?
(2)在第一阶段运动中,绳对重物做功W1为多大?
(3)滑轮在第一阶段运动中的机械效率η1和在第三阶段运动中的机械效率η3分别为多大?
28.(2016·杭州)小金用如图所示的实验装置测量杠杆的机械效率.实验时竖直向上拉动杠杆,使挂在杠杆下面的钩码缓缓上升.(支点和杠杆的摩擦不计)问:
(1)重为5N的钩码挂在A点时,人的拉力F为4N,钩码上升0.3m时,动力作用点C上升0.5m,此时机械效率η1为多大?
(2)小金为了进一步研究杠杆的机械效率与哪些因素有关,仍用该实验装置,将钩码移到B点,再次缓慢提升杠杆使动力作用点C仍然上升0.5m.问:人的拉力F与第一次相比??????? (选填“变大”“变小”或“不变”).比较此时的机械效率η2与η1的大小并用学过的知识给以推导.
29.(2020·杭州)杆秤是一种用来测量物体质量的工具。小金尝试做了如图所示的杆秤。在秤盘上不放重物时,将秤砣移至O点提纽处,杆秤恰好水平平衡,于是小金将此处标为0刻度。当秤盘上放一个质量为2kg的物体时,秤砣移到B处,恰好能使杆秤水平平衡测得OA=5cm,OB=10cm。
(1)计算秤砣的质量
(2)小金在B处标的刻度应为________kg。若图中OC=2OB,则C处的刻度应为________Kg
(3)当秤盘上放一个质量为2kg的物体时,若换用一个质量更大的秤砣,移动秤砣使杆秤再次水平平衡时,其读数________(选填“<”或“>”)2kg,由此可知一杆杄秤不能随意更换秤砣
30.(2019·杭州)如图甲,有一轻质杆,左右各挂由同种金属制成,质量分别为m1和m2(m1>m2)的实心物块后恰好水平平衡
(1)求左右悬挂点到支点O的距离L1与L2之比
(2)将两物分别浸没在水中,杆将会?? ▲?? (选填“左端下降”“右端下降”“仍然平衡”),试通过推导说明。
31.(2018·台州)图甲是一种壶口处配有自动开合小壶盖的电水壶。
(1)如图乙,电水壶底部的导线连接装置有铜环①、铜环②和铜柱③。经测试发现:①、②之间是绝缘的,②、③之间常温下有十几欧姆的电阻。则与水壶金属外壳相连的装置是________。
(2)图丙是自动开合小壶盖简化侧视图。OA是小壶盖,C是其重力作用点。B是小壶盖的配重。OB是配重柄。AOB能绕固定点O自由转动。请在答题纸图丙中作出小壶盖的重力G及其力臂L。
(3)已知:小壶盖质量为4克,OA=3厘米,OC=1.4厘米,OB=1厘米,∠AOB=135°.要求倒水时,壶身最多倾斜45°,小壶盖便自动打开;壶身竖直时,小壶盖在水平位置自动闭合。求配重B的质量取值范围。(配重柄质量和O点的摩擦均忽略不计, 2 取1.4)
32.(2018·绍兴)2018年3月28日绍兴风情旅游新干线开通试运行。“鉴湖号”城际列车从绍兴站驶出开往上虞站,两站相距40千米,列车运营速度120千米/小时.
(1)列车从绍兴站出发至少需要________分钟到达上虞站。
(2)在图中旅行箱和拉杆构成的杠杆中,能表示拉力F的力臂是________。
(3)列车牵引总功率为5152千瓦,表示的意义是________,并计算列车以运营速度匀速直线运行时所受水平阻力大小________(用科学计数法表示,保留两位小数)。
33.(2016·台州)桥式起重机在工业生产上有广泛应用.如图是某桥式起重机的示意图,水平横梁MN架在轨道A和B上,电动机D可沿横梁左右移动.横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计.
(1)电动机通过滑轮组,将质量为600千克的零件,以0.4米/秒的速度匀速吊高4米.求:电动机对零件做的功为多少焦?电动机的功率至少为多少瓦?(g取10牛/千克)
(2)已知横梁长度为L,零件质量为m,电动机吊着零件从M点出发并开始计时,以水平速度v匀速运动到N点,横梁对轨道A的压力F与时间t的关系式为:F=________.
34.(2016·衢州)如图为小柯在科技节中制作的“杠杆力臂演示仪”和“流体压强与流速关系演示仪”.
(1)如图甲(杠杆自身质量和摩擦忽略不计,固定装置未画出),O为支点,OA=OD=3OB=0.6米,CD=0.2米.在做背景的白纸上作有以O为圈心半径为0.2米的圆.在A点挂5牛顿的重物G,要使杠杆水平平衡,则作用在B点竖直向下的力FB应为________牛,撤去FB后,按图示方向分别施加FC、FD两个力,且毎次都使杠杆在水平位置平衡,则FC、FD大小关系为________.
(2)如图乙,在注射器A、B处分别扎一个等大的小孔,插入两根相同规格的硬质塑料管(连接处密封),并 在管上分别系一个未充气的同规格气球(连接处不漏气).先慢慢往外拉活塞,使注射器中充满空气,接着快速向内推动活塞,在此过程中可现察到A、B两孔处气球的鼓起情况是________(填序号).
①A孔处气球大②B孔处气球大③两个气球一样大
35.(2016·嘉兴)如图甲为塔式起重机简易示意图,塔式起重机主要用于房屋建筑中材料的输送及建筑构件的安装.(动滑轮重、绳重及摩擦均不计,g取10牛/千克)
(1)为保持平衡,起重臂的长度越长的塔式起重机,配备的平衡重的质量应越________.
(2)图乙为起重机钢丝绳穿绳简化示意图,滑轮a的作用是________.若钢丝绳能承受的最大拉力为3×104牛,则能吊起货物的质量不能超过________千克?
(3)若将重为1.2×104牛的货物由地面沿竖直方向匀速提升30米,再沿水平方向移动20米,则此过程中克服货物重力做功多少焦?
(4)若该起升电动机的效率为90%,将重为1.2×104牛的货物提升到30米的高度,用时50秒,则该起升电动机的实际功率是多少瓦?
答案解析部分
一、单选题
1.【答案】 C
【解析】【分析】(1)通过判断滑轮的种类判断它们的作用是否相同;
(2)使用滑轮组提升重物时,自由端的距离和物体上升高度之间的关系为:s=nh;
(3)定滑轮不省力不费力,且与拉力的方向无关;
(4)使用滑轮组时,要克服动滑轮的重力做功。
【解答】A.下面的滑轮是动滑轮,上面的滑轮是定滑轮,二者的作用不同,故A错误;
B.因为动滑轮上有2段绳子承担物重,因此拉力移动的距离是配重移动距离的2倍,故B错误;
C.使用定滑轮不省力不费力,且拉力的大小与方向无关,故C正确;
D.将配重提升相同高度,直接做的功为W=Gh,用该装置做的功为:W=(G+G动)h,因此二者不同,故D错误。
故选C。
2.【答案】 D
【解析】【分析】(1)功率计算公式P=Fv;(2)弹簧测力计的读数有拉着左侧滑轮的三根绳子决定;(3)由物体B的运动,判断出A对B有摩擦力,根据力的作用是相互的所以B对A也有摩擦力,根据A相对于地面静止可判断出A和地面之间是否有摩擦力;(4)滑动摩擦力的大小只与压力大小和表面粗糙程度有关,与B物体的运动速度无关。
【解答】A.F2的功率为0.6W,将左侧滑轮看成定滑轮时,这个滑轮组能省1/2的力,费2倍的距离,所以绳子自由端的运动速率为0.2m/s,由公式P=Fv=3N×0.2m/s=0.6W,说法正确,A错误;
B.弹簧测力计读数为9N,左侧滑轮有三根绳子拉着,每根绳的拉力都为3N,所以总拉力是9N,说法正确,B错误;
C.物体A和地面之间有摩擦力,因为B受到向左的拉力,向左做匀速直线运动,可知B受到平衡力的作用,B受到向左的拉力为6N,受到向右的摩擦力也为6N。由于力的作用是相互的,B也给A一个摩擦力且大小也为6N,方向向左,由于A保持静止所以A受到平衡力的作用,向应该受到向右的力也为6N,已知F1=4N,所以地面对A的摩擦力为2N方向向右,说法正确,C错误;
D.如果增大F2 , 物体A可能向左运动,由于滑动摩擦力的大小只与表面粗糙程度和压力的大小有关,而B对A的压力不变且粗糙程度也不变,所以滑动摩擦力不变,A物体的受力不变,所以仍为静止,说法错误,D正确。
故答案为:D
3.【答案】 A
【解析】【分析】根据杠杆的平衡条件分析。
【解答】当把铝条a放在铁条上时,铁条的重力G铁为阻力,作用在中点,那么阻力臂为:L2-La;动力为铝条a的重力Ga , 作用在它的中点处,动力臂为La2 ,
根据杠杆的平衡条件得到:G铁×L2-La=Ga×La2? ?①;
当把铝条b放在铁条上时,铁条的重力G铁为阻力,作用在中点,那么阻力臂为:L2-Lx;动力为铝条a的重力Ga , 作用在它的中点处,动力臂为Lx-Lb2 ,
根据杠杆的平衡条件得到:G铁×L2-Lx=Gb×Lx-Lb2 ②;
①÷②得到:
L2-LaL2-Lx=GaGb×La2Lx-Lb2 ③;
因为铝条a和b横截面积相等,根据公式G=ρVg=ρShg可知,铝条的重力与长度成正比,
即:GaGb=LaLb;
将其袋入③得到:L2-LaL2-Lx=LaLb×La2Lx-Lb2 ;
因为La
那么L2-LaL2-Lx
若Lb
故选A。
4.【答案】 A
【解析】【分析】使用滑轮时,轴的位置固定不动的滑轮称为定滑轮。定滑轮不省力,但是可以改变力的方向。属于滑轮原理的应用,和机械功的讨论。实质上是动力臂等于阻力臂的杠杆。轴的位置随被拉物体一起运动的滑轮称为动滑轮。动滑轮实质是动力臂等于2倍阻力臂的杠杆(省力杠杆)。它不能改变力的方向,但最多能够省一半的力,但是不省功。
【解答】A、滑轮组中的A滑轮是动滑轮,动滑轮是用于省力的;故A错误;
B、 当C伸长时,阻力臂增长,而动力和动力臂不变,所以阻力会增大,则对D杆的压力会变大;故B正确;
C、 当D伸长时,倾斜角增大,所以力F的力臂会变小;故C正确;
D、 H杆的作用是用于支持起重机,防止压力作用在轮胎上;故D正确;
故答案为:A。
5.【答案】 C
【解析】【分析】此滑轮组是由一个定滑轮和一个动滑轮组成的,根据图中绕线可知能省力也能改变力的方向,但会比较费距离。
【解答】A.两个滑轮均为定滑轮,和物体一起上升的滑轮为动滑轮,A错误;
B.人将绳子拉过1米,物体也上升1米,滑轮组省力但费距离,当人拉过1米时,物体上升只有0.5米,B错误;
C.物体匀速上升时,人对绳子的拉力为200牛,此滑轮组能省 12 的力,F= 12 G,C正确;
D.使用该装置不能省力,但能改变力的方向,此滑轮组即能省力又能改变力的方向,D错误。
故选C
6.【答案】 C
【解析】【分析】本题所用滑轮组是水平的,计算过程要注意,拉力的大小是摩擦力的一半,拉力移动的路程是物体移动的路程的2倍(动滑轮由两股绳子拉着)。该滑轮为动滑轮,拉力F的大小和弹簧测力计的示数一样,因为物体做匀速运动,所以物体受到的力是平衡力,利用力的平衡可以计算摩擦力的大小;利用W=Fs公式计算拉力做的功,再利用功率的公式计算拉力F的功率。
【解答】∵物体做匀速运动,
∴摩擦力f=2F=2×10N=20N;故A、B错误;
v绳子=2v=2m/s,
水平拉力F做功的功率为P=Fv=10×2m/s=20W,故C正确;
s=vt=1s×1m/s=1m,
1秒内滑轮对物体M做功为W=Fs=20N×1m=20J,故D错误;
故选C
7.【答案】 C
【解析】【分析】不计摩擦、动滑轮重和绳重,对于动滑轮,F甲=2G,F乙= 12 G;根据P=Fv比较甲乙的功率.
【解答】解:
由题知,两装置都不计摩擦、动滑轮重和绳重,提升物体的重相同,
甲图,拉力作用在动滑轮的轴上,费一倍的力,即F甲=2G;
乙图,拉力作用在绳子自由端,省一半的力,即F乙= 12 G,故F甲>F乙 , AD错误;
物体上升的速度相同,则拉力端的速度分别为:v甲= 12 v物 , v乙=2v物 ,
甲图拉力的功率:P甲=F甲v甲=2G× 12 v物=Gv物;
乙图拉力的功率:P乙=F乙v乙= 12 G×2v物=Gv物 , 故P甲=P乙 , C正确,B错误;
故选C.
8.【答案】 D
【解析】【分析】由图示的斜面、滑轮组、动滑轮、杠杆分别求出拉力F1、F2、F3、F4 , 最后比较各力的大小,确定哪个拉力最小。
【解答】解:A、由图示的斜面知F1×L=G×h,F1×4m=G×2m,F1=12G;
B、由图示可知,滑轮组承重绳子的股数为3,拉力F2=G3;
C、这是动滑轮的特殊使用方法,物体挂在动滑轮一侧的绳子上,拉动滑轮的轮轴,此时拉力F3=2G;
D、由图可知L4∶LG=(1m+3m)∶1m=4∶1,由杠杆平衡条件可得:F4×L4=G×LG,F4=G×LGL4=G4;
因此最小拉力是F4。
故选D。
9.【答案】 A
【解析】【分析】(1)当P向右运动时,对于P而言,它受到的向左的阻力是地面给它的摩擦力,Q给它的摩擦力、定滑轮的绳子给它的拉力这三个力的总和。
(2)要使P做匀速运动,它受到向右的拉力与向左的阻力相互平衡。
【解答】以Q为研究对象, Q与P之间动摩擦因数是μ,物块的质量都是m, 所以Q给P的摩擦力也为f1=μmg;P做匀速运动,则Q也做匀速运动,由平衡条件可得绳子对Q的拉力为μmg,所以同一条定滑轮上的绳子给P的拉力也为μmg; P与桌面之间的动摩擦因数是μ,两物块的质量都是m,地面对P的滑动摩擦力大小f2=2μmg。F=T+f1+f2=μmg+μmg+2μmg=4μmg,A正确。
故答案为:A
?
10.【答案】 C
【解析】【分析】拉小球上升时,根据W有用=Gh计算有用功,根据W总=Fs计算总功,根据η=W有用W总×100%计算机械效率。
【解答】由题细管缠绕在圆体上后相当于一个斜面,由图a到b点的高度h=5×0.12m=0.6m,
拉小球上升时,有用功W有用=Gh=1N×0.6m=0.6J;总功W总=Fs=0.8N×1m=0.8J,
所以缠绕在圆柱体上的细管的机械效率:η=W有用W总×100%=0.6J0.8J×100%=75% , C正确。
故答案为:C
11.【答案】 A
【解析】【分析】杠杆的分类主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂。结合生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆。
【解答】A、镊子在使用过程中,动力臂小于阻力臂,是费力杠杆,故A符合题意;
B、瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆,故B不符合题意;
C、羊角锤在使用过程中,动力臂大于阻力臂,是省力杠杆,故C不符合题意;
D、天平称物体质量,动力臂等于阻力臂,为了称量重量,故D不符合题意。
故选A
12.【答案】 C
【解析】【分析】杠杆可分为:省力杠杆、费力杠杆和等臂杠杆,可以从动力臂和阻力臂的大小关系进行判断,当动力臂大于阻力臂时,是省力杠杆;当动力臂等于阻力臂时,是等臂杠杆;当动力臂小于阻力臂时,是费力杠杆。
【解答】A、刀刃很薄是减小了受力面积,从而增大压强,故A错误;
B、铡刀当动力臂大于阻力臂时,是省力杠杆,故B错误;
C、甘蔗放在a点比b点阻力臂小,根据F1L1=F2L2 , 可知甘蔗放在a点比b点更易被切断,故C正确;
D、动力臂垂直于力的方向,可知F2动力臂大于F1 , 因此F2更省力,故D错误。
故选C
13.【答案】 D
【解析】【分析】使用滑轮时,轴的位置固定不动的滑轮称为定滑轮。定滑轮不省力,但是可以改变力的方向。属于滑轮原理的应用,和机械功的讨论。实质上是动力臂等于阻力臂的杠杆。控制变量在进行科学实验的概念,是指那些除了实验因素(自变量)以外的所有影响实验结果的变量,这些变量不是本实验所要研究的变量,所以又称无关变量、无关因子、非实验因素或非实验因子。
【解答】AC、由四套装置图可知,在定滑轮的两侧各安装一个弹簧测力计,然后分别测量出钩码的重力和拉力;测量钩码重力的弹簧测力计应上方固定,所以AC不符合题意;
BD、为了控制变量,所以弹簧测力计应都是固定上方,下方可动,故B错误;D正确;
故答案为:D。
14.【答案】 C
【解析】【分析】根据图片可知,这座桥是左右对称的。根据二力平衡的原理计算出顶层砖块对右侧中间层砖块的压力。当中间层的砖块要向左倾倒而未倒时相当于一个杠杆,支点就是最下层砖块的左上顶点,此时阻力就是中间层砖块的重力G,作用在它的中心;动力就是顶层砖块的压力,根据杠杆的平衡条件计算出右侧中间层砖块跨出的长度,最后根据桥的最大跨度=底层砖块长+中间层跨出长度×2计算即可。
【解答】如图,顶层砖对两侧砖的压力F为砖重力的一半,即F=G/2。以中间层右侧的砖为研究对象,以最下层砖块的左上顶点为支点,假设砖块的右侧离与下层砖块的左上顶点(支点)的距离为x,则顶层右侧砖给予中间层右侧的砖块压力的力臂为x,中间层右侧的砖受到的阻力(即为其自身的重力)的力臂为(12cm-x),根据应用杠杄平衡条件有:G/2×x=G×(12cm-x),解得x=8cm ,可推知此时该砖恰好能平衡砖的最大跨度=24cm+2×8cm=40cm。
故答案为:C
15.【答案】 A
【解析】【分析】掌握杠杆的五个要素:支点、动力、阻力、动力臂、阻力臂。根据动力和阻力画出动力臂和阻力臂;注意力臂是一条线段,而非直线。(1)支点是杠杆绕着转动的固定点,动力和阻力都是外界作用在杠杆上的力,都是杠杆受到的力.力臂是支点到力的作用线的垂直距离。(2)画力臂的方法:首先确定支点;然后找到动力和阻力,并用虚线延长动力和阻力的作用线;然后由支点向力的作用线引垂线,支点到垂足的距离就是力臂。
【解答】支点是杠杆绕着转动的固定点,动力和阻力都是外界作用在杠杆上的力,都是杠杆受到的力,分析可知O是支点,动力F1作用N点,阻力F2作用在M点;N点向下施力,M点受力方向向上,
故选A
二、填空题
16.【答案】 (1)1.4
(2)21;热传递
【解析】【分析】(1)首先根据s=nh计算出拉力移动的距离,再根据W总=Fs计算出拉力做的总功,最后根据W有=W总η计算克服物体A重力做的功;
(2)酒精燃烧放出的热量与水吸收的热量相同,首先根据Q=cm△t计算出水吸收的热量,再根据m酒=Q酒q酒计算需要燃烧酒精的质量。改变内能的两种方式:①做功;②热传递。
【解答】(1)拉力移动的距离据s=nh=0.1m×2=0.2m;
拉力做的总功W总=Fs=10N×0.2m=2J;
克服物体A重力做的功W有=W总η=2J×70%=1.4J。
(2)水吸收的热量为:Q=cm△t=4.2×103J/(kg?℃)×2kg×(100℃-25℃)=6.3×105J;
要燃烧酒精的质量m酒=Q酒q酒=6.3×105J3.0×107J/kg=0.021kg=21g。
上述过程中,水的内能增加是通过热传递的途径实现的。
17.【答案】 (1)改变力的方向
(2)省力
【解析】【分析】(1)定滑轮的作用是改变拉力的方向,而不能省力;
(2)比较动力臂和阻力臂的大小,然后对杠杆进行分类。
【解答】(1)根据乙图可知,如果不使用定滑轮,那么拉力的方向应该向上,使用定滑轮后拉力的方向变为向下,因此定滑轮的作用是:改变力的方向;
(2)如下图所示:
因为动力臂大于阻力臂,所以该状态下的桶盖属于省力杠杆。
18.【答案】 (1)4.8
(2)B
【解析】【分析】(1)动滑轮可以省一半的力,据此根据弹簧测力计的示数可确定物体的重;(2)根据杠杆的平衡条件,在阻力一定的情况下,减小阻力臂可以省力.本题主要考查了对动滑轮和杠杆的应用,理解各自的工作特点,是正确解答的关键.
【解答】解:(1)图中弹簧测力计的分度值为0.2N,其示数为2.4N;在不计摩擦及滑轮和绳子的自重的情况下,动滑轮可以省一半的力.
故物体的重力G=2F=2×2.4N=4.8N;(2)剪刀在使用时相当于杠杆,根据杠杆的平衡条件,阻力不变,动力臂不变,将被剪物体应放在B点时,阻力臂更小,所以更省力.
故答案为:(1)4.8;(2)B.
19.【答案】 动力臂大于阻力臂;
【解析】【分析】(1)根据杠杆的平衡条件可知,如果动力臂大于阻力臂,那么为省力杠杆;如果动力臂小于阻力臂,那么为费力杠杆;如果二者相同,那么为等臂杠杆,不省力也不费力;
(2)首先判断开瓶器对瓶盖的作用力方向,然后根据相互作用力原理判断阻力的方向。
【解答】(1)开瓶器的在瓶盖上的部分是支点,动力作用在末端,而阻力作用在瓶盖下边,因为动力臂大于阻力臂,所以它能省力;
(2)当作用在开瓶器最右端的手向上用力时,咬合在瓶盖下面的牙对瓶盖的作用力向上;根据相互作用力原理可知,开瓶器上的阻力与它方向相反,即向下,如图:
20.【答案】 (1)60
(2)90
(3)10~90
【解析】【分析】杠杆原理 亦称“杠杆平衡条件”。要使杠杆平衡,作用在杠杆上的两个力(动力和阻力)的大小跟它们的力臂成反比。动力×动力臂=阻力×阻力臂。
【解答】(1)若 G=30 牛,以木棒为研究对象,木棒受力平衡,故木棒受台面的支持力为60N, 台面收到木棒的压力与木棒受到台面的支持力为相互作用力,即为60N;
(2)若要使木棒右端下沉,则B点为支点,根据杠杆平衡条件GB×0.3=GA×0.9, 解得GB=90N,即B端挂的物体至少要大于90牛;
(3)若 B 端挂物体后,木棒仍在水平台面上静止,以A点为支点,根据杠杆平衡条件GB ×0.9=GA×0.3,解得则 GB=10N, 即G 的取值范围为.:10~90牛。
故答案为:(1)60;(2)90;(3)10~90。
21.【答案】 (1)4
(2)C
【解析】【分析】(1)杠杆平衡时动力×动力臂=阻力×阻力臂,可用公式F1· L1=F2·L2计算出G2;(2)力臂OB折过一定角度后其余都不变,要使杠杆继续平衡必须使G2的力臂长度与原来相同就行。
【解答】(1)G1·LAO =G2· LBO? 2N×0.2m=G2×0.1m? G2=4N;(2)由乙图可知当将G2移动到②点处时力臂与原来相等,所以当G2移动到②处时杠杆继续保持平衡。
故答案为:1、4N;2、C
22.【答案】 20;60;540
【解析】【分析】(1)根据杠杆平衡条件求出拉力的大小; (2)肩对木棒的支持力大小为F=FA+FB; (3)对人进行受力分析即可解答。
【解答】解: (1)由题根据杠杆的平衡条件有:F×OB=G×OA, 即:F×(0.6m﹣0.2m)=40N×0.2m, 所以:F=20N;即手压木棒的压力大小为20N;
(2) 肩对木棒的支持力大小为F′=F+G=20N+40N=60N;
(3)以人为整体,人处于静止状态,受到人、物体的重力和地面对人体的支持力是一对平衡力,大小相等,即F支=G人+G物=mg+G物=50kg×10N/kg+40N=540N。
又因为人对地面的压力大小和地面对人体的支持力是一对相互作用力,大小相等,即F压=F支=540N
故答案为:20;60;540。
三、实验探究题
23.【答案】 (1)大
(2)将八个风力板的迎风面朝南放置
(3)每天结束时,以倾倒风力板中记录风力最大的作当天最强风力
【解析】【分析】此时的风力板构成了一个杠杆,动力时风力,阻力是重力。
【解析】(1)风力板受风力和重力作用,所以,当风力为动力时,重力则为阻力,风力板越重越不容易倾倒。所以压重板上的铁板越重,风力板倾倒时记录的风力越大 。
(2)在开阔的水平地面放置风力探测仪时,要使风力探测仪面向风吹来的方向,因为在南风盛行的地方,所以小明应将八个风力板的迎风面朝南放置。
(3) 每天结束时,以倾倒风力板中记录风力最大的作当天最强风力。
故答案为:(1)大;(2) 将八个风力板的迎风面朝南放置 ;(3) 每天结束时,以倾倒风力板中记录风力最大的作当天最强风力
四、解答题
24.【答案】 (1)定滑轮
(2)减小摩擦
(3)W=Fs=Gh=20牛×1.5米=30焦
(4)晾衣杆可看作是一个杠杆,左侧绳与晾衣杆的交点为杠杆的支点,l2为悬挂点到支点的距离
根据杠杆平衡公式:F1×l1=F2×l2
可得l2= F1×l1F2 = 15牛×20厘米×1020牛 =150厘米
挂在9、10、11三个孔上晾晒会损坏晾衣架。
【解析】【分析】(1)根据这个简单机械的工作特点推断它的种类;
(2)减小摩擦的方法:①减小压力;②减小接触面的粗糙程度;③改变接触面;③添加润滑剂;
(3)根据W=Gh计算对衣服做的功;
(4)可以将晾衣杆看作一个杠杆,左侧绳子与晾衣杆的交点为支点,衣服的重力为阻力,衣服的悬挂点到支点的距离为阻力臂;右侧绳子的拉力为动力,动力臂就是晾衣杆的长度,根据杠杆的平衡条件,计算出阻力臂的长度,然后对小孔的位置进行定位,从而确定钢丝绳会断裂的小孔位置。
【解答】(1)根据图片可知,安装在天花板内的机械,应该能够旋转,并且它的位置固定不变,因此应该是定滑轮。
(2)使用一段时间后,对手摇器的转轴添加润滑剂,目的是减小摩擦。
(3)至少对衣服做功:W=Fs=Gh=20N×1.5m=30J;
(4)晾衣杆可看作是一个杠杆,左侧绳与晾衣杆的交点为杠杆的支点,l2为悬挂点到支点的距离;
根据杠杆平衡公式:F1×l1=F2×l2;
可得:?l2= F1×l1F2=15N×20cm×1020N=150cm;??
那么可以悬挂的最右边的孔为:150cm20cm+1≈8;
因此挂在9、10、11三个孔上晾晒会损坏晾衣架。
25.【答案】 (1)解:s=2×2米=4米
W=Fs=18牛×4米=72焦
(2)解: P=Wt=72J4s=18W
(3)解:f=0.35G=0.35×100牛=35牛
G轮=2F-f=2×18N-35N=1N
【解析】【分析】该题主要考查滑轮组的相关计算,并综合考查了功率和做功的计算;
【解答】(1)滑轮组省力费距离,由可知动滑轮上的绳子段数n,而绳子自由端移动的距离是物体移动的n倍;所以绳子自由端移动的距离为S=2×2m=4m;W=FS=18N×4m=72J;故答案为:S=2×2m=4m;W=FS=18N×4m=72J;(2)功率是做功与时间的比值,而由题可知W=72J;t=4s;所以 P=Wt=72J4s=18W ;故答案为: P=Wt=72J4s=18W ;(3)人通过滑轮组拉动物体匀速运动,说明处于平衡状态;所以动力等于阻力;阻力包括物体受到的摩擦力、滑轮的重力两部分;而滑轮组省力的,则拉力的n倍等于阻力;f=0.35G=0.35×100牛=35牛; G轮=2F-f=2×18N-35N=1N ;故答案为:f=0.35G=0.35×100牛=35牛; G轮=2F-f=2×18N-35N=1N ;
故答案为:(1)S=2×2m=4m;W=FS=18N×4m=72J;(2) P=Wt=72J4s=18W ;(3)f=0.35G=0.35×100牛=35牛; G轮=2F-f=2×18N-35N=1N 。
26.【答案】 (1)解:物体的重力为:G=mg=100kg×10N/kg=1000N;
动滑轮的重力为:G轮=m轮g=8kg×10N/kg=80N;
则拉力为:F= 1n (G+G轮)= 12 ×(1000N+80N)=540N;
答:拉力的大小为540N;
(2)拉力移动的距离为s=2h=2×3m=6m;
拉力做的功为:W=Fs=540N×6m=3240J;
拉力的功率为:P= Wt = 3240J30s =108W.
答:这段时间内人拉绳子做功的功率为108W.
【解析】【分析】(1)根据公式F= 1n (G+G轮)求出拉力;(2)根据功和功率的计算公式解答.
27.【答案】 (1)V排=V金=Sh=0.05m2×0.2m=0.01m3
F浮=ρ水V排g=1.0×103kg/m3×10N/kg×0.01m3=100N
(2)从重物上表面刚露出水面到其下表面刚离开水面,用时t2=4s:上升高度为物体的高h=0.2m,得上升速度v===0.05m/s;
第一阶段上升高度s=vt1=0.05m/s×40s=2m
绳对重物做的功W=F1s=140N×2m=280J
(3)第一阶段中,此时拉力的大小F=13(140N+60N)=2003牛 , 此时的机械效率η=W有用W总=F绳hF人×3h×100%=140牛×h200牛3×3h×100%≈70%第三阶段中,此时绳子给予物体的拉力的大小等于物体的重力,由物体第一阶段在水中受到的浮力和绳子给予物体的拉力可得G物=100牛+140牛=240牛,拉力的大小F=13(240N+60N)=100牛,此时的机械效率
【解析】【分析】(1) 在第一阶段运动中,V排就是物体的体积,在利用阿基米德原理进行计算即可。
(2)因为重物一直做竖直向上的匀速直线运动,所以第一阶段和第二阶段的速度是一样的。利用第二阶段的路程和时间求出物体移动的速度,从而求出第一阶段物体通过的路程,最后用公式W=Fs求出所做的功。
(3)机械效率等于有用功除以总功;在此滑轮组中, F人=13(F物+G动),s=3h。人拉绳子所做的是总功,人克服物体和动滑轮的阻力所做的功是有用功。
28.【答案】 (1)有用功:W有用=Gh=5N×0.3m=1.5J;
总功:W总=Fs=4N×0.5m=2J,
机械效率:η= W有用W总 ×100%= 1.5J2J ×100%=75%;
答:机械效率η1为75%
(2)变小;
钩码的悬挂点在A点时,由于杠杆的重力会阻碍杠杆转动,
则由杠杠的平衡条件得:G?OA+G杠杆? 12 OC=F?OC;
悬挂点移至B点时,由杠杠的平衡条件得G?OB+G杠杆? 12 OC=F′?OC,
观察比较可知,悬挂点移至B点时,OB<OA,即钩码重力的力臂变小,所以拉力F也变小;
杠杆的机械效率:η= W有用W总 ?= W有用W有用+W额 ?= 11+W额W有用 ;
因为杠杆升高的高度不变,所以克服杠杆自重所做的额外功不变(即W额=G杠杆?h杠杆不变);由于悬挂点B更接近支点,所以钩码提升的高度减小,根据W有用=Gh可知,有用功减小;
从上面η的表达式可知:W有用减小、W额不变,所以 W额W有用 变大,分母变大,η就减小;即η2<η1 .
【解析】【分析】(1)根据W=Gh求出有用功;根据W=Fs求出总功,根据η= W有用W总 求出机械效率;(2)将钩码的悬挂点从A点移至B点,改变了钩码重力的力臂,根据杠杆平衡条件分析,改变了弹簧测力计的拉力,改变了弹簧测力计的拉力做功的多少,改变了机械效率的高低.本题考查的是学生对有用功、总功、额外功、机械效率计算公式的理解和掌握,同时还考查杠杠平衡条件的应用.
29.【答案】 (1)根据杠杆平衡条件:F1l1=F2l2 , 得m1gl1=m2gl2 , 即:m1l1=m2l2 , 2kg×5cm=m2×10cm,得m2=1kg
(2)2;4
(3)<
【解析】【分析】(1)将O点看作杠杆的支点,秤砣的重力看做阻力,OB为阻力臂;物体的重力为动力,动力臂为OA,根据杠杆的平衡条件计算即可;
(2)根据此时物体的质量确定B处标的刻度值。再次根据杠杆的平衡条件计算此时物体的质量即可;
(3)秤砣的重力相当于阻力,根据杠杆的平衡条件分析阻力臂的长度变化即可。
【解答】(1)将O点看作杠杆的支点,秤砣的重力看做阻力,OB为阻力臂;物体的重力为动力,动力臂为OA,
根据杠杆平衡条件:F1l1=F2l2,
即:m1gl1=m2gl2,
m1OA=m2OB;
2kg×5cm=m2×10cm;
解得:m2=1kg?。
(2)因为秤砣在B处平衡时,物体的质量为2kg,所以小金在B处标的刻度应为2kg;
若图中OC=2OB,
根据杠杆的平衡条件得到:G物×OA=G秤砣×OC;
m物g×OA=m秤砣g×OC;
m物×OA=m秤砣×OC;
m物×5cm=1kg×20cm;
解得:m物=4kg;
因此在C处的刻度应为4kg;
(3)根据杠杆的平衡条件得到:
G物×OA=G秤砣×OC';
m物×OA=m秤砣×OC';
当物体的质量m物 , OA不变时,秤砣的质量m秤砣增大,那么阻力臂OC'变小,
因此其读数<2kg。
30.【答案】 (1)解:∵杠杆平衡时有:F1×L1=F2×L2
∴m1g×L1=m2g×L2
变形得到:L1:L2=m2:m1
(2)仍然平衡;
以浸没于水的物体为研究对象进行受力分析:
F拉+F浮=m物g
F拉=m物g-F浮=m物g-ρ水gV物=(1- ρ水ρ物 )m物g
所以;F拉1×L1=(1- ρ水ρ物 )m1gL1
F2×L2=(1- ρ水ρ物 )m2gL2
∵m1gL1=m2gL2
∴F拉1L1=F拉2L2
因此杠杆仍然平衡
【解析】【分析】(1)将左边的物体重力看作动力,右边的物体重力看作阻力,根据杠杆的平衡条件列出平衡关系式,借助数学运算得到左右悬挂点到支点O的距离L 1与L 2之比;
(2)当两个物体浸没在水中时,它们都会受到浮力,根据二力平衡条件得到: F拉+F浮=m物g 。据此计算出它们作用在杠杆上的拉力F拉1和F拉2;接下来分别计算杠杆两边动力和动力臂的乘积以及阻力和阻力臂的乘积,借助(1)中的结果对它们的大小进行比较即可。
31.【答案】 (1)铜环
(2)
(3)当配重柄水平时,可求出配重的最小质量,杠杆示意图如图2:
OD= 12 ×OC= 12 ×1.4cm=1cm,根据杠杆的平衡条件:
G1l1=G2l2 , m1gl1=m2gl2 , m2=m1 m1ODOB = 4g×1cm1cm =4g;
当小壶盖水平时,可求出配重的最大质量,杠杆示意图如图3:
OE= 12 ×OB= 12 ×1cm=0.71cm,
根据杠杆的平衡条件:
G1l1′=G2l2′,m1gl1′=m2gl2′,
m2′=m1 OCOE = 4g×1.4cm0.71cm ≈7.89g。
【解析】【分析】(1)外壳是金属,应该与火线、零线绝缘,根据已知条件分析。
(2)重力G方向竖直向下,根据力臂的定义做出重力的力臂;
(3)根据杠杠的平衡条件,当配重柄水平时,配重的质量最小;当水壶盖水平时,配重的质量最大,利用数学知识结合杠杆的平衡条件求解。
【解答】(1)铜是导体,由题意,铜环①、铜环②之间是绝缘的,说明之间有底盘的绝缘体;②、③之间常温下有十几欧姆的电阻,为加热电阻,故与水壶金属外壳相连的装置只能是铜环①,否则与②或③相连则有触电的危险。
(2)水壶盖的重力G方向竖直向下,根据力臂的定义做出重力的力臂,如下图1所示:
(3)当配重柄水平时,可求出配重的最小质量,杠杆示意图如图2:
OD=12×OC=12×1.4cm=1cm , 根据杠杆平衡条件可得:G1l1=G2l2 , 即m1gl1=m2gl2 , m,2=m1=m1ODOB=4g×1cm1cm=4g;
当壶盖水平时,可求出配重的最大质量,杠杆示意图如图3:
OE=12×OB=12×1cm=0.71cm , 根据杠杆平衡条件可得:G1l'1=G2l'2 , m1gl'1=m2gl'2 , m,2=m1=m1OCOE=4g×1.4cm0.71cm=7.89g
故答案为:(1)铜环①;(2)如图1所示;(3)配重B的质量取值范围4g---7.89g
32.【答案】 (1)20
(2)l1
(3)列车每秒钟做功5152千焦;1.55×105N
【解析】【分析】力的作用线到转动轴的垂直距离。与动力对应的力臂叫动力臂,与阻力对应的力臂叫阻力臂。功率是指物体在单位时间内所做的功的多少,即功率是描述做功快慢的物理量。功的数量一定,时间越短,功率值就越大。求功率的公式为功率=功/时间。
【解答】(1) t=SV=40km120km/h=13h=13×60min=20min ;故答案为:20;(2)力臂是支点到力的垂直距离,图中的杠杆O是支点,要找O点到F的垂直线段即可;故答案为:l1;(3)功率是用来表示物体做功快慢的物理量,所以5152千瓦表示牵引力每秒做功5152kJ;∵P= Wt=F?st =F·v?? v=120km/h=33.33m/s
∴F= Pv=5152×103W33.33m/s =1.55×105N??? f=F=1.55×105N;故答案为:1.55×105N;
故答案为:(1)20;(2)l1;(3)列车每秒钟做功5152千焦;1.55×105N。
33.【答案】 (1)电动机对零件做的功:
W=gh=mgh=600kg×10N/kg×4m=2.4×104J,
因横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计,
所以,拉力做的功即为克服零件重力所做的功,
则电动机对零件做功的功率:
P=Wt=ght=mght =mgv=600kg×10N/kg×0.4m/s=2.4×103W,
则电动机的最小功率为2.4×103W;
(2)mg-mgvLt
【解析】【分析】(1)知道零件的质量和提升的高度,根据W=Gh=mgh求出电动机对零件做的功,横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计,拉力做的功即为克服零件重力所做的功,根据P= Wt = Ght = mght =mgv求出电动机对零件做功的功率即为电动机的最小功率;(2)横梁对轨道A的压力F和轨道对横梁的支持力是一对相互作用力,根据v= st 可得AD段的长度,从而得出轨道对横梁的支持力和重物的力臂,根据杠杆的平衡条件得出等式即可求出轨道对横梁的支持力与t的关系,再根据相互作用力的关系得出得出答案.本题考查了功和功率的计算以及速度公式、杠杆平衡条件的应用,利用相互作用力的条件把横梁对轨道A的压力F转化为轨道对横梁的支持力来处理是关键.
【解答】解:(1)电动机对零件做的功:
W=Gh=mgh=600kg×10N/kg×4m=2.4×104J,
因横梁、电动机、挂钩、滑轮、钢索、导线的质量以及滑轮上的摩擦均不计,
所以,拉力做的功即为克服零件重力所做的功,
则电动机对零件做功的功率:
P= Wt = Ght = mght =mgv=600kg×10N/kg×0.4m/s=2.4×103W,
则电动机的最小功率为2.4×103W;(2)横梁对轨道A的压力F和轨道对横梁的支持力是一对相互作用力,
把MN看作一根杠杆,B为支点,A端对横梁的支持力为动力,零件的重力为阻力(其它重力和摩擦力不计);
由v= st 可得,t时间内AD段的长度:LAD=vt,
则零件重力的力臂:LG=L﹣LAD=L﹣vt,
轨道A对横梁支持力的力臂为L,
由杠杆的平衡条件可得:F支持?L=G?(L﹣vt),
则F支持= G·(L-vt)L =G﹣ GvtL =mg﹣ mgvL t,
由相互作用力的特点可知,横梁对轨道A的压力F与时间t的关系式:
F=F支持=mg﹣ mgvL t.
答:(1)电动机对零件做的功为2.4×104J,电动机的功率至少为2.4×103W;(2)mg﹣ mgvL t.
34.【答案】 (1)15;FC=FD
(2)②
【解析】【分析】(1)根据杠杆平衡条件计算作用在B点竖直向下的力FB的大小;通过比较FC、FD两个力的力臂与FB的力臂的关系,根据杠杆平衡条件分析FC、FD大小关系;(2)流体的压强跟流速有关,流速越大,压强越小.此题考查杠杆平衡条件的应用、流体压强和流速的关系,难点在(1),关键是从图示中得出FC、FD两个力的力臂均与FB的力臂相等,然后利用杠杆平衡条件分析解答.
【解答】解:(1)根据杠杆平衡条件可得:G×OA=FB×OB,
OA=3OB=0.6m,则OB=0.2m,
所以,作用在B点竖直向下的力FB= = =15N;
由图可知,FC、FD两个力的力臂均与FB的力臂相等,都是圆的半径,阻力和阻力臂不变,
撤去FB后,按图示方向分别施加FC、FD两个力,且毎次都使杠杆在水平位置平衡,
根据杠杆平衡条件可知,FC、FD大小关系为FC=FD;(2)由图可知B的下端注射器的横截面积大,A的下端注射器的横截面积小,快速向内推动活塞,B的下端空气流速小,压强大,A的下端空气流速大,压强小,所以,
在此过程中可现察到A、B两孔处气球的鼓起情况是B孔处气球大.
故答案为:(1)15;(2)FC=FD;(2)②.
35.【答案】 (1)大
(2)改变力的方向;6000
(3)由于水平移动时,重力方向上没移动距离,故水平移动过程中重力没做功;
W=Fs=Gh=1.2×104N×30m=3.6×105J,
答:此过程中克服货物重力做功3.6×105J;
(4)有用功W有用=Gh=1.2×104牛×30米=3.6×105焦,
总功W总= W有用η = 3.6×105J90% ?=4×105焦,
实际功率P= W总t = 4×105J50s ?=8000W.
答:该起升电动机的实际功率是8000瓦.
【解析】【分析】(1)因动力臂及动力的乘积不变,则由杠杆的平衡条件可知配重与配重臂的关系;(2)根据滑轮的特点分析其作用;根据滑轮组特点确定绳子段数求出物体重力;再结合重力公式求出质量;(3)根据功的公式W=Fs求出克服重力做功大小;(4)求出有用功,利用效率公式求总功,再利用P= Wt 求实际功率.
【解答】解:(1)由杠杆的平衡条件F1L1=F2L2(动力×动力臂=阻力×阻力臂)可得:F2= F1L1L2 ,由此可知当阻力臂和动力不变时,阻力与动力臂成正比;即动力臂越大,阻力越大;动力臂越小,阻力越小.故为保持平衡,起重臂的长度越长的塔式起重机,配备的平衡重的质量应越大;(2)图示中滑轮a为定滑轮,其作用是改变用力的方向;
由题意可知该滑轮组承担总重的绳子有2段,故G=2F=3×104牛×2=6×104牛
由G=mg可得:m= Gg=6×104N10N/kg ?=6000千克;
同课章节目录
