北师大版八年级数学上册 4.3.1一次函数的图像——正比例函数的图像及性质课件
文档属性
| 名称 | 北师大版八年级数学上册 4.3.1一次函数的图像——正比例函数的图像及性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 13.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 11:43:31 | ||
图片预览





文档简介
(共34张PPT)
北师大版八年级数学(上册)
目标引领
明确任务
一.会利用描点法或两点法画出正比例函数的图象.
二.经历知识的归纳探究过程、掌握正比例函数及其图象的性质.
一、复习回顾:
函数有哪些表示方法?
_______、_______、_______。
一次函数的关系式?__________________
正比例函数的关系式?__________________
关系式法
列表法
图象法
y=kx+b
(k≠0)
y=kx
(k≠0)
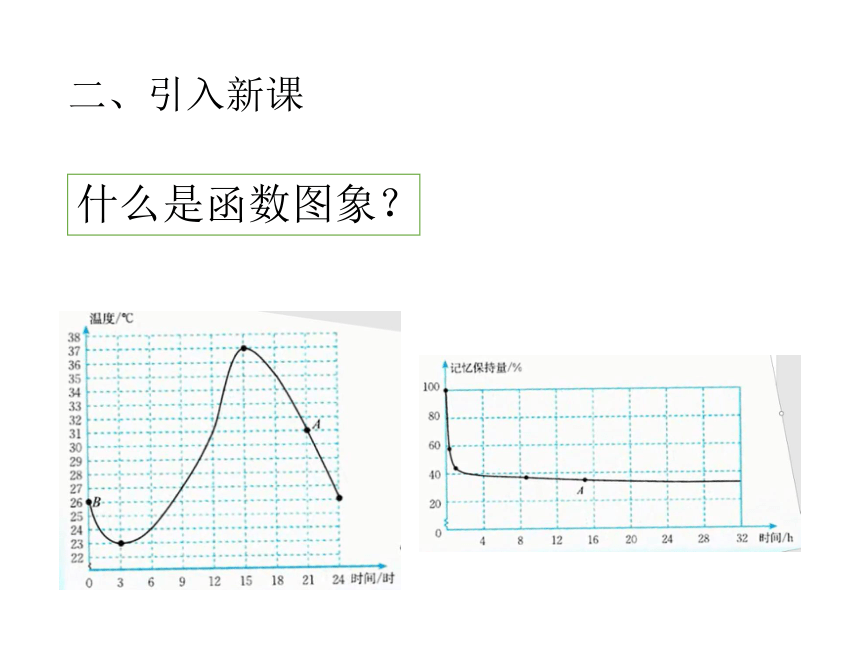
二、引入新课
什么是函数图象?
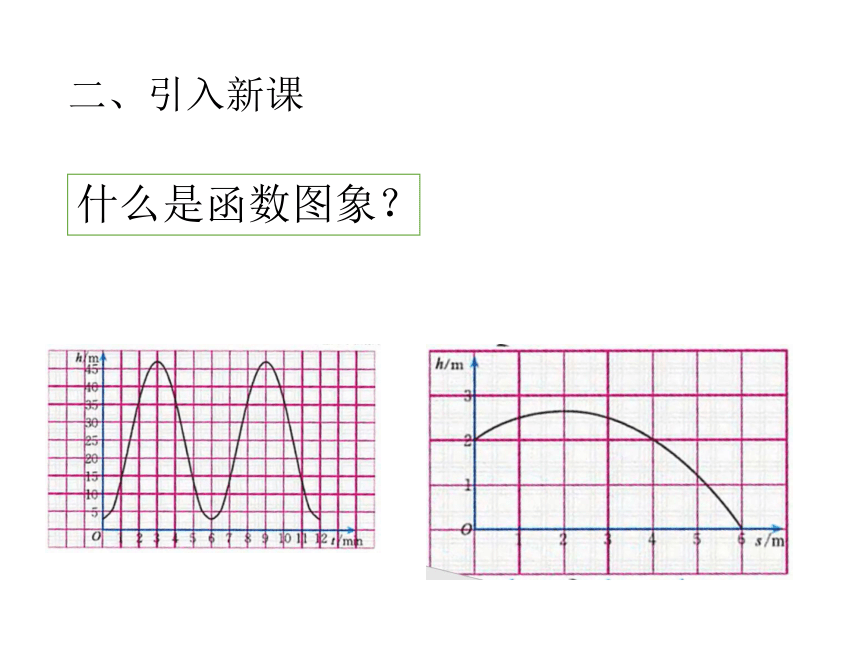
二、引入新课
什么是函数图象?
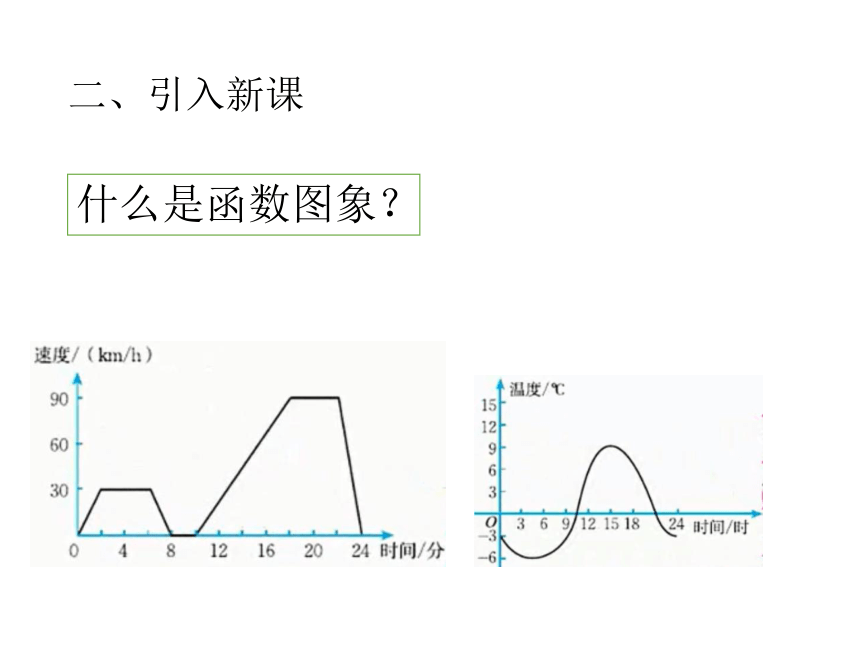
二、引入新课
什么是函数图象?
二、引入新课
一分钟时间同学们预习课本83页第一段,了解函数图象的概念,并闭卷填空。
把一个函数自变量的每一个值与对应的函数值分别作为点的横坐标和纵坐标,在直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象。
画函数图象的一般步骤:________、________、________。
列表
描点
连线
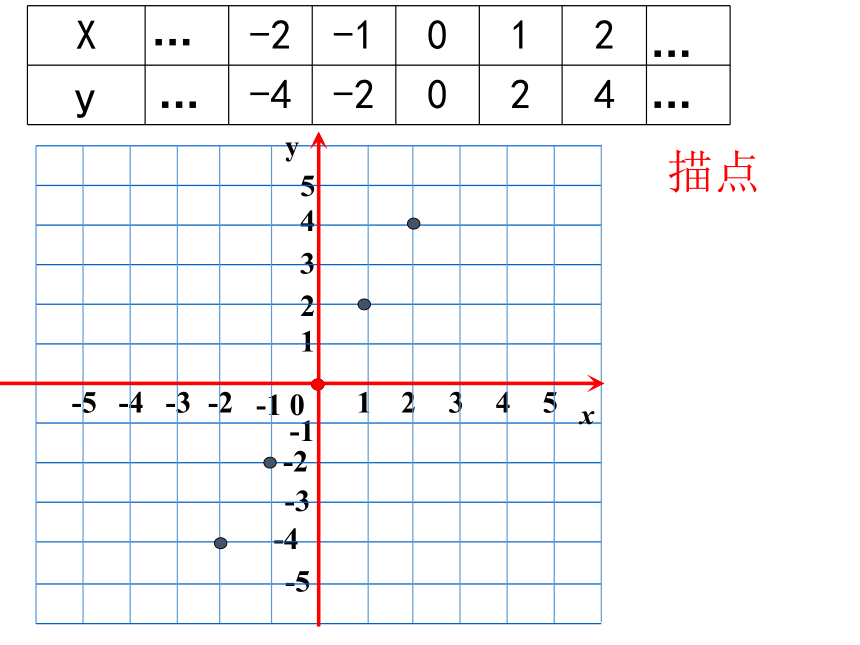
例1
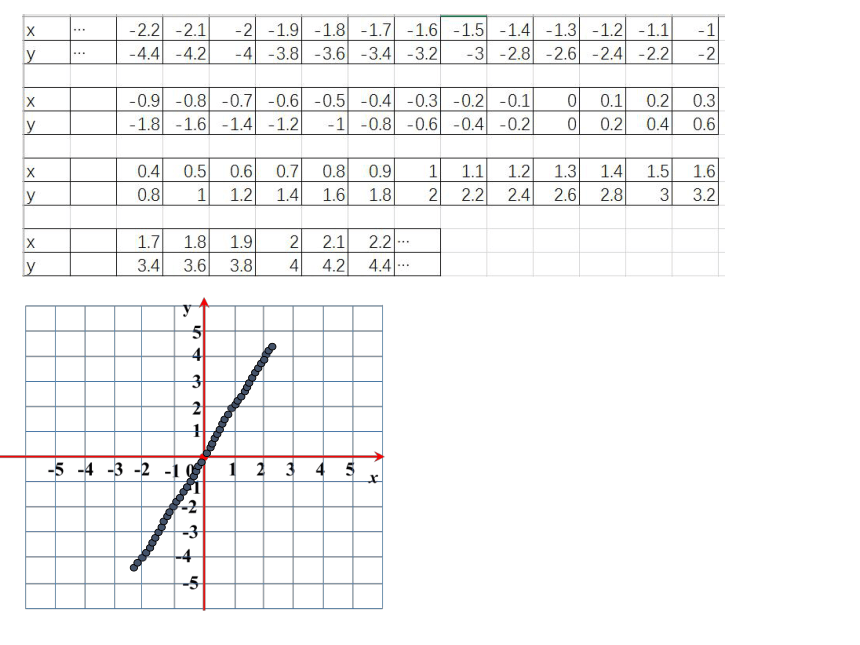
画出正比例函数y=2x的图象.
解:列表:
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
三、活动探究
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
X
-2
-1
0
1
2
-4
-2
0
2
4
…
…
…
…
y
描点
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
y=2x
X
-2
-1
0
1
2
-4
-2
0
2
4
…
…
…
…
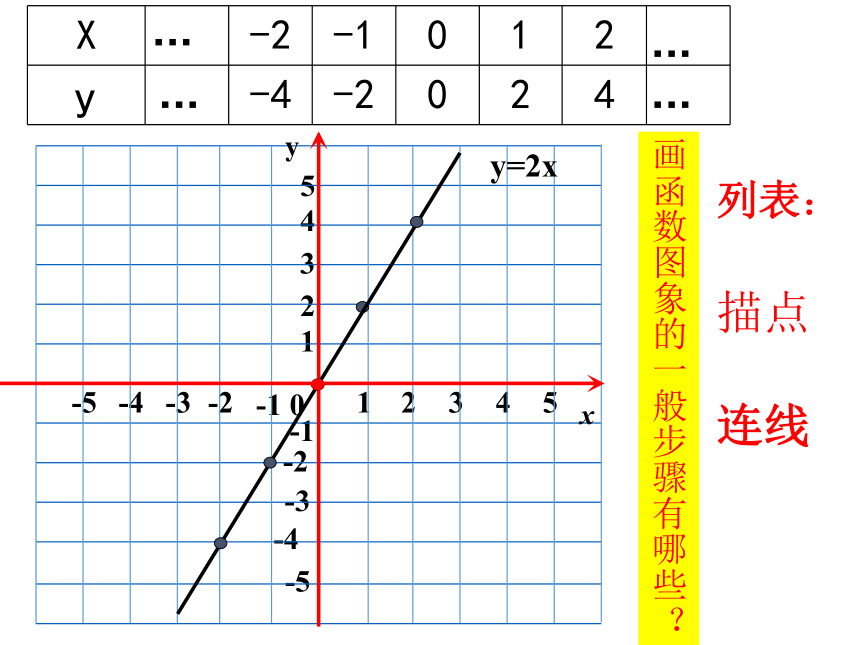
画函数图象的一般步骤有哪些?
列表:
描点
连线
y
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
X
-2
-1
0
1
2
…
…
…
…
y
请同学们自己动手,在第二个坐标系中画出正比例函数y=-2x的图象。
y=-2x
思考:怎样画正比例函数的图象最简单?_____点确定一条直线,所以描点时只需要____个点,即________和________,列表也可以简化。
x
0
1
y
0
?
两点法
轻松自测
两
两
原点
原点以外任意一点
(0,0)和(1,k)
函数y=kx(k≠0)
k
0
0
0
0.3
4
画正比例函数的图象,是经过(0,0)和(1,_____)的直线
画正比例函数的图象,是经过(0,0)和(___,
___)的直线
画正比例函数的图象,是经过(
__,
___
)和(
____,
___
)的直线
3
1
2
0
0
1
1
k>0
画正比例函数的图象,是经过
(
__,
___
)和(
____,
___
)的直线
画正比例函数的图象,是经过
(
__,
___
)和(
____,
___
)的直线
画正比例函数的图象,是经过
(
__,
___
)和(
____,
___
)的直线
0
0
-3
1
0
0
-1
0
1
-2
1
0
k<0
观察两个组正比例函数图象的异同点可以发现:(小组讨论、归纳性质)
函数y=kx(k≠0)
正比例函数图象
经过象限
示意草图
变化趋势
增减性
k>0
一条经过___点的___线
?
?
从左向右____
y随x的增大而_____
k<0
?
?
从左向右____
y随x的增大而_____
观察动图
试概括图象的变化趋势和函数值的增加性
观察两个组正比例函数图象的异同点可以发现:
函数y=kx(k≠0)
正比例函数图象
经过象限
示意草图
变化趋势
增减性
k>0
一条经过___点的___线
?
?
从左向右____
y随x的增大而_____
k<0
?
?
从左向右____
y随x的增大而_____
原点
直线
一三
二四
上升
下降
增大
减少
轻松自测
2和4
<
y=-3x
小组讨论课本84页第一个“议一议”,并阐述结论及依据理由。
B
A
C
对于y=-3x中,当x=1000时,y=-3000,
对应点(1000,-3000)在不在y=-3x的图象上?
正比例的表达式和图象的关系
y=-3x
x=3,
y=-9
(3,-9)
函数图象
表达式
解
点
正比例的表达式和图象的关系
y=-3x
x=3,
y=-9
(3,-9)
函数图象
表达式
解
点
结论:正比例函数的表达式和图象是完全对等的,即一一对应的关系。
轻松自测
下列哪些点在正比例函数y=-6x的图象上_______
A、(1,6)
B、(-1,6)
C、(0,6)
D、(1,-6)
2、如果函数y=kx(k≠0)的图象经过点(5,-10),那么k=_____
B、D
-2
想一想
第一组正比例函数、、中,随着x值的增大,y的值都增加了,其中哪一个增加得更快?小组讨论给出理由。
第二组正比例函数中,随着x值的增大,y的值都减小了,其中哪一个减小得更快?小组讨论给出理由。
正比例函数中,k>0时,k越______,直线越陡,_________上升的越_____。
大
相应的函数值
快
正比例函数中,k<0时,k越______,直线越陡,_________下降的越_____。
小
相应的函数值
快
从图象上我们可以发现:
1.正比例函数中,k>0时,k越______,直线越陡,_________上升的越_____。
2.正比例函数中,k<0时,k越_____,直线越陡,_________下降的越_____。
3.总结:正比例函数中,k的_________越大,直线越陡,__________上升或者下降的越快。
大
相应的函数值
快
小
相应的函数值
快
绝对值
相应的函数值
轻松自测
如右边图所示,k1、k2、k3之间的大小关系是__________
?
k3
<
k1
<
k2
四、课外拓展
在同一直角坐标系中画出和的图象,用量角器测量两直线的夹角。猜想一下夹角与两个正比例函数解析式的关系,并尝试验证。
两条直线的k互为负倒数时,两条直线互相垂直。
本课小结:
4.3.1一次函数的图象——正比例函数的图象及性质
1、画函数图象的一般步骤:
2、正比例函数图象是一条经过_______点的______线
3、两点法画正比例函数图象,绘制出过(0,___)和(1,____)的直线。
4、正比例函数中,当k>0时,图象经过_______象限,y的值随着x值的增大而______;当k<0时,图象经过_______象限,y的值随着x值的增大而______。
5、正比例函数的表达式和图象是_________的,即________的关系。
6、正比例函数中,________越大,直线越陡,_________上升或者下降的越快。
北师大版八年级数学(上册)
目标引领
明确任务
一.会利用描点法或两点法画出正比例函数的图象.
二.经历知识的归纳探究过程、掌握正比例函数及其图象的性质.
一、复习回顾:
函数有哪些表示方法?
_______、_______、_______。
一次函数的关系式?__________________
正比例函数的关系式?__________________
关系式法
列表法
图象法
y=kx+b
(k≠0)
y=kx
(k≠0)
二、引入新课
什么是函数图象?
二、引入新课
什么是函数图象?
二、引入新课
什么是函数图象?
二、引入新课
一分钟时间同学们预习课本83页第一段,了解函数图象的概念,并闭卷填空。
把一个函数自变量的每一个值与对应的函数值分别作为点的横坐标和纵坐标,在直角坐标系内描出相应的点,所有这些点组成的图形叫做该函数的图象。
画函数图象的一般步骤:________、________、________。
列表
描点
连线
例1
画出正比例函数y=2x的图象.
解:列表:
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
三、活动探究
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
X
-2
-1
0
1
2
-4
-2
0
2
4
…
…
…
…
y
描点
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
y=2x
X
-2
-1
0
1
2
-4
-2
0
2
4
…
…
…
…
画函数图象的一般步骤有哪些?
列表:
描点
连线
y
-5
-4
-3
-2
-1
5
4
3
2
1
-1
0
-2
-3
-4
-5
1
2
3
4
5
x
y
X
-2
-1
0
1
2
…
…
…
…
y
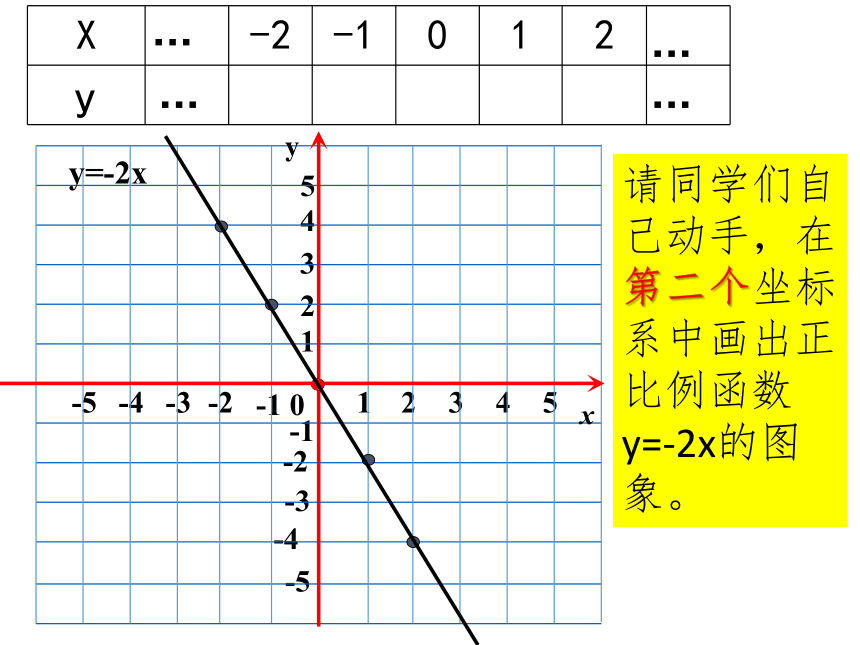
请同学们自己动手,在第二个坐标系中画出正比例函数y=-2x的图象。
y=-2x
思考:怎样画正比例函数的图象最简单?_____点确定一条直线,所以描点时只需要____个点,即________和________,列表也可以简化。
x
0
1
y
0
?
两点法
轻松自测
两
两
原点
原点以外任意一点
(0,0)和(1,k)
函数y=kx(k≠0)
k
0
0
0
0.3
4
画正比例函数的图象,是经过(0,0)和(1,_____)的直线
画正比例函数的图象,是经过(0,0)和(___,
___)的直线
画正比例函数的图象,是经过(
__,
___
)和(
____,
___
)的直线
3
1
2
0
0
1
1
k>0
画正比例函数的图象,是经过
(
__,
___
)和(
____,
___
)的直线
画正比例函数的图象,是经过
(
__,
___
)和(
____,
___
)的直线
画正比例函数的图象,是经过
(
__,
___
)和(
____,
___
)的直线
0
0
-3
1
0
0
-1
0
1
-2
1
0
k<0
观察两个组正比例函数图象的异同点可以发现:(小组讨论、归纳性质)
函数y=kx(k≠0)
正比例函数图象
经过象限
示意草图
变化趋势
增减性
k>0
一条经过___点的___线
?
?
从左向右____
y随x的增大而_____
k<0
?
?
从左向右____
y随x的增大而_____
观察动图
试概括图象的变化趋势和函数值的增加性
观察两个组正比例函数图象的异同点可以发现:
函数y=kx(k≠0)
正比例函数图象
经过象限
示意草图
变化趋势
增减性
k>0
一条经过___点的___线
?
?
从左向右____
y随x的增大而_____
k<0
?
?
从左向右____
y随x的增大而_____
原点
直线
一三
二四
上升
下降
增大
减少
轻松自测
2和4
<
y=-3x
小组讨论课本84页第一个“议一议”,并阐述结论及依据理由。
B
A
C
对于y=-3x中,当x=1000时,y=-3000,
对应点(1000,-3000)在不在y=-3x的图象上?
正比例的表达式和图象的关系
y=-3x
x=3,
y=-9
(3,-9)
函数图象
表达式
解
点
正比例的表达式和图象的关系
y=-3x
x=3,
y=-9
(3,-9)
函数图象
表达式
解
点
结论:正比例函数的表达式和图象是完全对等的,即一一对应的关系。
轻松自测
下列哪些点在正比例函数y=-6x的图象上_______
A、(1,6)
B、(-1,6)
C、(0,6)
D、(1,-6)
2、如果函数y=kx(k≠0)的图象经过点(5,-10),那么k=_____
B、D
-2
想一想
第一组正比例函数、、中,随着x值的增大,y的值都增加了,其中哪一个增加得更快?小组讨论给出理由。
第二组正比例函数中,随着x值的增大,y的值都减小了,其中哪一个减小得更快?小组讨论给出理由。
正比例函数中,k>0时,k越______,直线越陡,_________上升的越_____。
大
相应的函数值
快
正比例函数中,k<0时,k越______,直线越陡,_________下降的越_____。
小
相应的函数值
快
从图象上我们可以发现:
1.正比例函数中,k>0时,k越______,直线越陡,_________上升的越_____。
2.正比例函数中,k<0时,k越_____,直线越陡,_________下降的越_____。
3.总结:正比例函数中,k的_________越大,直线越陡,__________上升或者下降的越快。
大
相应的函数值
快
小
相应的函数值
快
绝对值
相应的函数值
轻松自测
如右边图所示,k1、k2、k3之间的大小关系是__________
?
k3
<
k1
<
k2
四、课外拓展
在同一直角坐标系中画出和的图象,用量角器测量两直线的夹角。猜想一下夹角与两个正比例函数解析式的关系,并尝试验证。
两条直线的k互为负倒数时,两条直线互相垂直。
本课小结:
4.3.1一次函数的图象——正比例函数的图象及性质
1、画函数图象的一般步骤:
2、正比例函数图象是一条经过_______点的______线
3、两点法画正比例函数图象,绘制出过(0,___)和(1,____)的直线。
4、正比例函数中,当k>0时,图象经过_______象限,y的值随着x值的增大而______;当k<0时,图象经过_______象限,y的值随着x值的增大而______。
5、正比例函数的表达式和图象是_________的,即________的关系。
6、正比例函数中,________越大,直线越陡,_________上升或者下降的越快。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
