华师大版九年级数学下册 26.2 二次函数的图形与性质 同步测试题(Word版 有答案)
文档属性
| 名称 | 华师大版九年级数学下册 26.2 二次函数的图形与性质 同步测试题(Word版 有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览


文档简介
116078001130300012319000026.2 二次函数的图形与性质 同步测试题
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 将y=x2+6x+7化为y=a(x-h)2+k的形式,h,k的值分别为( )
A.3,-2 B.-3,-2 C.3,-16 D.-3,-16
?
2. 抛物线y=3x2,y=-3x2,y=13x2都有的性质是(? ? ? ? )
A.开口向下 B.对称轴是y轴
C.都有最低点 D.y随x的增大而减小
?3. 抛物线y=-2x2-12x-23的顶点坐标是(? ? ? ? )
A.3,-5 B.3,5 C.-3,-5 D.-3,5
?
4. 对于二次函数y=x2-2mx-3,有下列说法:
①它的图象与x轴有两个公共点;
②如果当x≤1时y随x的增大而减小,则m=1;
③如果将它的图象向左平移3个单位后过原点,则m=-1;
④如果当x=4时的函数值与x=2008时的函数值相等,则当x=2012时的函数值为-3.
其中正确的个数是( )
A.1 B.2 C.3 D.4
?
5. 已知抛物线y=ax2-2ax-1(a≠0),下列四个结论:①当a>0时,在对称轴的右边,y随x的增大而增大;②函数图象的对称轴是x=-1;③当a=1时,图象经过点(-1,?2);④当a=-2时,函数图象与x轴没有交点,其中正确的共有( )
A.4个 B.3个 C.2个 D.1个
?
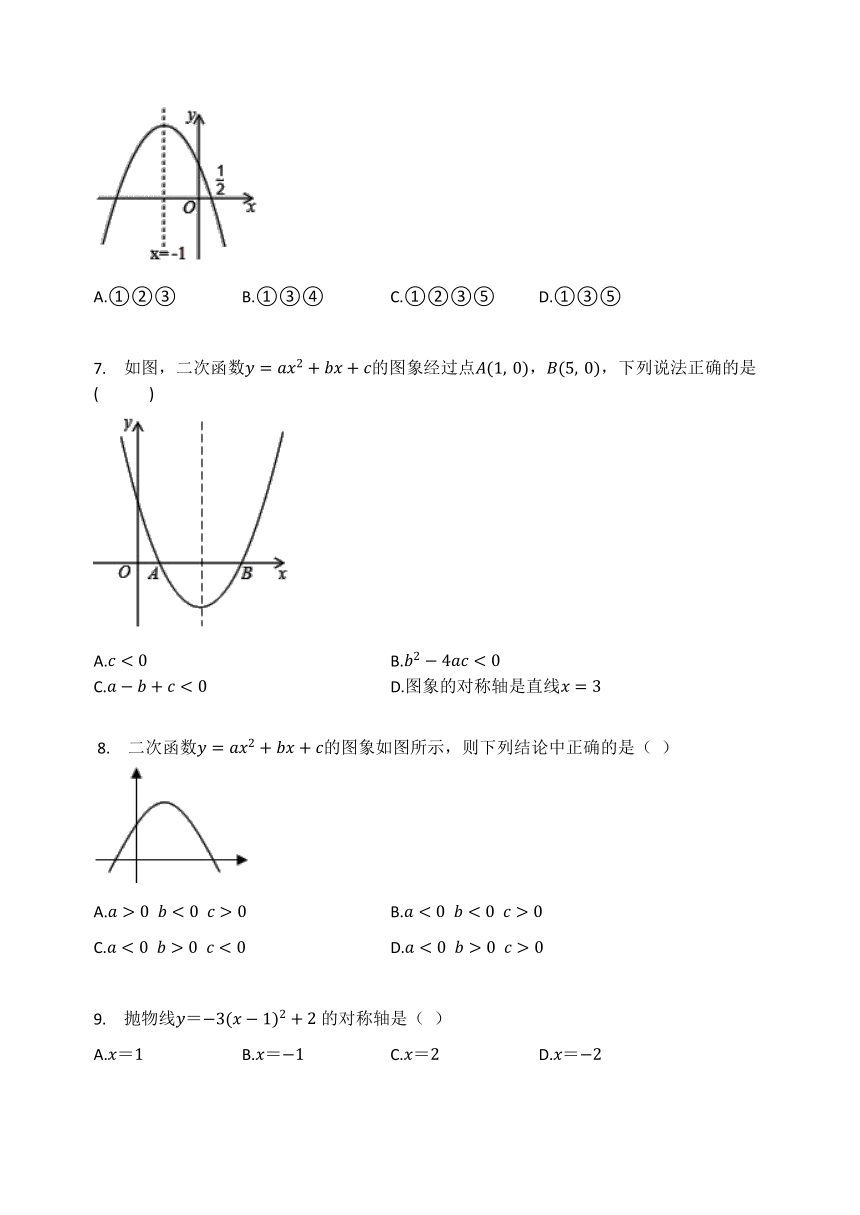
6. 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,?0),有下列结论:
①abc>0;?②a-2b+4c=0;?③25a-10b+4c=0;?④3b+2c>0;⑤a-b≥m(am-b).
其中所有正确的结论是( )
A.①②③ B.①③④ C.①②③⑤ D.①③⑤
?
7. 如图,二次函数y=ax2+bx+c的图象经过点A(1,?0),B(5,?0),下列说法正确的是(? ? ? ? )
A.c<0 B.b2-4ac<0
C.a-b+c<0 D.图象的对称轴是直线x=3
?8. 二次函数y=ax2+bx+c的图象如图所示,则下列结论中正确的是( )
A.a>0??b<0??c>0 B.a<0??b<0??c>0
C.a<0??b>0??c<0 D.a<0??b>0??c>0
?
9. 抛物线y=-3(x-1)2+2的对称轴是( )
A.x=1 B.x=-1 C.x=2 D.x=-2
?
10. 如果点A(1,?3),B(m,?3)是抛物线y=a(x-4)2+h上两个不同的点,那么m的值为(? ? ? ? )
A.4 B.5 C.6 D.7
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 二次函数y=ax2+6x+a的最大值是8,则a=________.
?
12. 抛物线y=ax2+bx+c开口向上,对称轴是直线x=1,A(-2,?y1),B(0,?y2),C(2,?y3)在该抛物线上,则y1,y2,y3大小的关系是________.
?
13. 已知抛物线的顶点为(-1,?-3),与y轴的交点为(0,?-5),则此抛物线的解析式是________.
?
14. 二次函数y=-(x-1)2+8的最大值是________.
?
15. 用配方法把y=x2+2x+4化为y=a(x+h)2+k的形式为________.
?
16. 抛物线y=ax2+bx+c过点A(1,?0),B(3,?0),则此抛物线的对称轴是直线x=________.
?
17. 如果二次函数y=x2+bx+c配方后为y=(x-2)2+1,那么c的值为________.
?
18. 点A(2,?y1)、B(3,?y2)是二次函数y=-x2+2x+m的图象上两点,则y1与y2的大小关系为y1________?y2(填“>”、“<”、“=”).
?
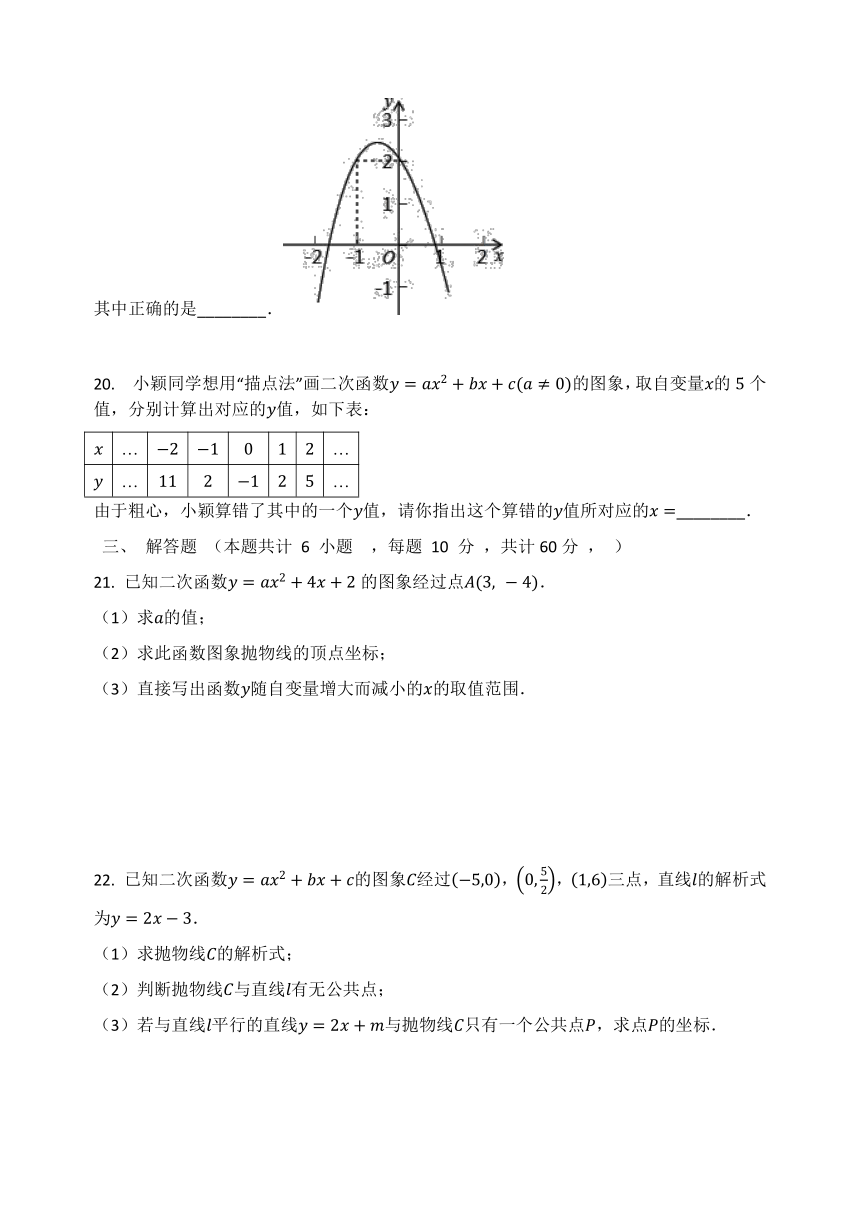
19. 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,?2),且与x轴交点的横坐标分别为x1、x2,其中-2①a-b+c=2;②abc>0;③4a-2b+c<0;④2a-b<0.
其中正确的是________.
?
20. 小颖同学想用“描点法”画二次函数y=ax2+bx+c(a≠0)的图象,取自变量x的5个值,分别计算出对应的y值,如下表:
x
…
-2
-1
0
1
2
…
y
…
11
2
-1
2
5
…
由于粗心,小颖算错了其中的一个y值,请你指出这个算错的y值所对应的x=________.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 , ) ?
21. 已知二次函数y=ax2+4x+2的图象经过点A(3,?-4).
(1)求a的值;
(2)求此函数图象抛物线的顶点坐标;
(3)直接写出函数y随自变量增大而减小的x的取值范围.
?
22. 已知二次函数y=ax2+bx+c的图象C经过-5,0,0,52,1,6三点,直线l的解析式为y=2x-3.
(1)求抛物线C的解析式;
(2)判断抛物线C与直线l有无公共点;
(3)若与直线l平行的直线y=2x+m与抛物线C只有一个公共点P,求点P的坐标.
?
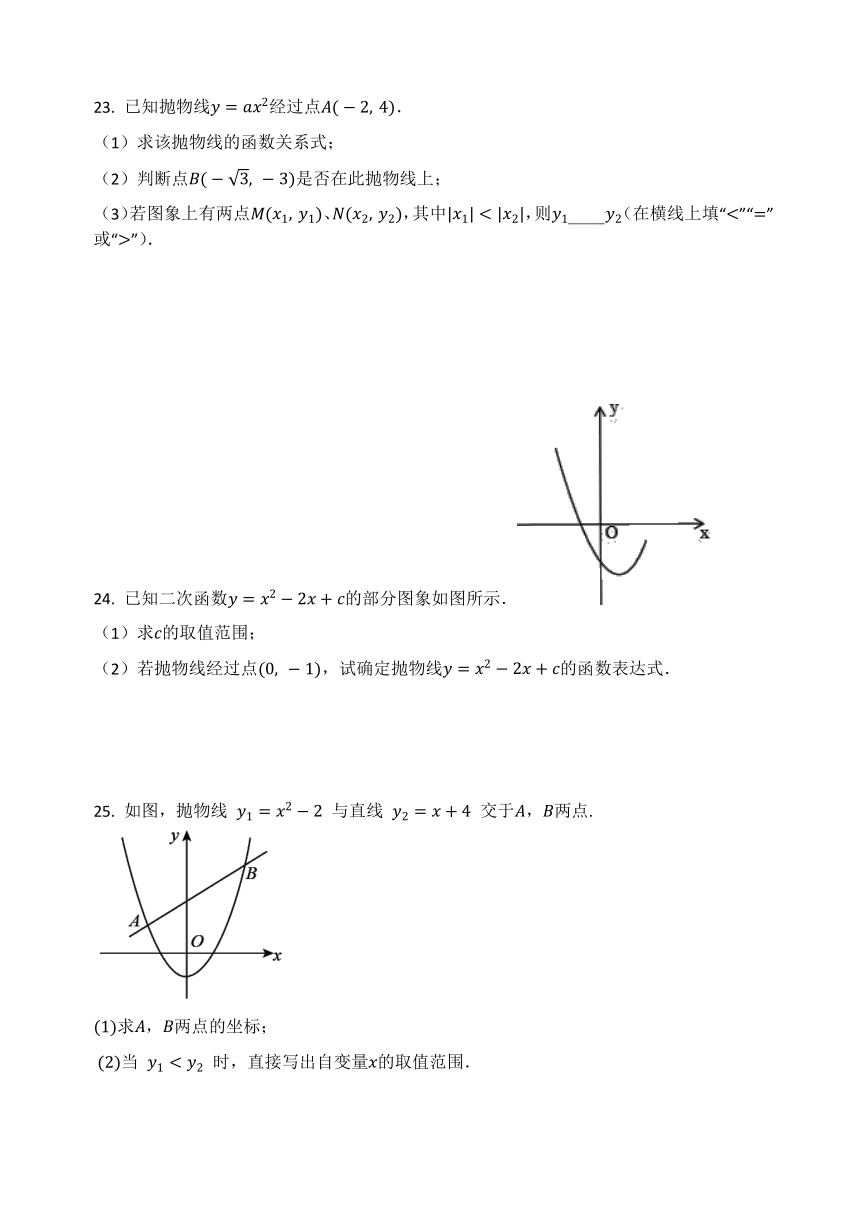
23. 已知抛物线y=ax2经过点A(-2,?4).
(1)求该抛物线的函数关系式;
(2)判断点B(-3,?-3)是否在此抛物线上;
(3)若图象上有两点M(x1,?y1)、N(x2,?y2),其中|x1|<|x2|,则y1________y2(在横线上填“<”“=”或“>”).
?
24. 已知二次函数y=x2-2x+c的部分图象如图所示.
(1)求c的取值范围;
(2)若抛物线经过点(0,?-1),试确定抛物线y=x2-2x+c的函数表达式.
?
25. 如图,抛物线 y1=x2-2 与直线 y2=x+4 交于A,B两点.
(1)求A,B两点的坐标;
(2)当 y1?
26. 在平面直角坐标系xOy中,抛物线y=-x2+2bx+b2+1的对称轴与x轴交于点A,将点A向左平移b个单位,再向上平移3-b2个单位,得到点B.
(1)求点B的坐标(用含b的式子表示);
(2)当抛物线经过点(0,?2),且b>0时,求抛物线的表达式;
(3)若抛物线与线段AB恰有一个公共点,结合图象,直接写出b的取值范围.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:∵ y=x2+6x+7=x2+6x+9-9+7=(x+3)2-2,
∴ h=-3,k=-2.
故选:B.
2.
【答案】
B
【解答】
解:在y=3x2中,可知其开口向上,对称轴为y轴,有最低点;
在y=-3x2中,可知其开口向下,对称轴为y轴,有最高点;
在y=13x2中,可知其开口向上,对称轴为y轴,有最低点;
∴ 三抛物线共有的性质是对称轴为y轴.
故选B.
3.
【答案】
C
【解答】
解:∵ y=-2x2-12x-23=-2x+32-5,
∴ 抛物线的顶点坐标为-3,-5.
故选C.
4.
【答案】
B
【解答】
解:①∵ △=(-2m)2-4×1×(-3)=4m2+12>0,
∴ 它的图象与x轴有两个公共点,故本小题正确;
②∵ 当x≤1时y随x的增大而减小,
∴ 对称轴直线x=--2m2×1≥1,
解得m≥1,故本小题错误;
③∵ 将它的图象向左平移3个单位后过原点,
∴ 平移前的图象经过点(3,?0),
代入函数关系式得,32-2m?3-3=0,
解得m=1,故本小题错误;
④∵ 当x=4时的函数值与x=2008时的函数值相等,
∴ 对称轴为直线x=4+20082=1006,
∴ --2m2×1=1006,
解得m=1006,
∴ 函数关系式为y=x2-2012x-3,
当x=2012时,y=20122-2012×2012-3=-3,故本小题正确;
综上所述,结论正确的是①④共2个.
故选B.
5.
【答案】
C
【解答】
∵ 抛物线y=ax2-2ax-1(a≠0),
∴ 当a>0时,抛物线开口向上,在对称轴的右边,y随x的增大而增大,故①正确,
函数图象的对称轴是直线x=--2a2a=1,故②错误,
当a=1时,y=x2-2x-1,当x=-1时,y=2,故③正确,
当a=-2时,y=-2x2+4x-1,当y=0时,-2x2+4x-1=0,则△=42-4×(-2)×(-1)=8>0,故当a=-2时,函数图象与x轴有两个交点,故④错误,
6.
【答案】
D
【解答】
由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴ abc>0,故①正确;
直线x=-1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以-b2a=-1,可得b=2a,
a-2b+4c=a-4a+4c=-3a+4c,
∵ a<0,
∴ -3a>0,
∴ -3a+4c>0,
即a-2b+4c>0,故②错误;
∵ 抛物线y=ax2+bx+c的对称轴是x=-1.且过点(12,?0),
∴ 抛物线与x轴的另一个交点坐标为(-52,?0),
当x=-52时,y=0,即a(-52)2-52b+c=0,
整理得:25a-10b+4c=0,故③正确;
∵ b=2a,a+b+c<0,
∴ 12b+b+c<0,
即3b+2c<0,故④错误;
当x=-1时,a-b+c≥am2-bm+c,
∴ a-b≥m(am-b),故⑤正确;
7.
【答案】
D
【解答】
解:A,由于二次函数y=ax2+bx+c的图象与y轴交于正半轴,所以c>0,故A错误;
B,二次函数y=ax2+bx+c的图象与x轴有2个交点,所以b2-4ac>0,故B错误;
C,当x=-1时,y>0,即a-b+c>0,故C错误;
D,因为A(1,?0),B(5,?0),所以对称轴为直线x=1+52=3,故D正确.
故选D.
8.
【答案】
D
【解答】
解:∵ 抛物线开口向下,
∴ a<0;
又∵ 抛物线的对称轴在y轴的右侧,
∴ x=-b2a>0,
∴ b>0,
而抛物线与y轴的交点在x轴上方,
∴ c>0.
故选D.
9.
【答案】
A
【解答】
令x-1=0,则x=1.
10.
【答案】
D
【解答】
解:点A(1,?3),B(m,?3)是抛物线y=a(x-4)2+h上两个不同的点,
得(1,?3)与(m,?3)关于对称轴x=4对称,
m-4=4-1,
解得m=7.
故选D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
-1
【解答】
解:
当a<0时,二次函数有最大值,其公式为ymax=4ac-b24a,
∴ 4a2-624a=8,整理可得a2-8a-9=0,
解得a=9(舍去)或a=-1,
故答案为:-1.
12.
【答案】
y1>y2=y3
【解答】
∵ 抛物线y=ax2+bx+c开口向上,对称轴是直线x=1,
∴ 抛物线上的点离对称轴越远,对应的函数值就越大,
∵ x取-2时所对应的点离对称轴最远,x取0与2时所对应的点离对称轴一样近,
∴ y1>y2=y3.
13.
【答案】
y=-2x2-4x-5
【解答】
解:根据题意设y=a(x+1)2-3,
将(0,?-5)代入得:a-3=-5,
解得:a=-2,
则抛物线解析式为y=-2(x+1)2-3=-2x2-4x-5.
故答案为:y=-2x2-4x-5
14.
【答案】
8
【解答】
∵ y=-(x-1)2+8,
∴ 此函数的顶点坐标是(1,?8),
即当x=1时,函数有最大值8.
15.
【答案】
y=(x+1)2+3
【解答】
y=x2+2x+4
=(x2+2x+1)+3
=(x+1)2+3,
即y=(x+1)2+3.
16.
【答案】
2
【解答】
解:∵ 点A(1,?0),B(3,?0)的纵坐标相等,
∴ A、B两点是抛物线上的两个对称点,
∴ 对称轴是直线x=1+32=2.
17.
【答案】
5
【解答】
∵ y=(x-2)2+1
=x2-4x+4+1
=x2-4x+5,
∴ c的值为5.
18.
【答案】
<
【解答】
解:∵ 二次函数y=x2+2x+m的图象的对称轴是x=-1,
在对称轴的右面y随x的增大而增大,
∵ 点A(2,?y1)、B(3,?y2)是二次函数y=x2+2x+m的图象上两点,
2<3,
∴ y1故答案为:<.
19.
【答案】
①②③④
【解答】
解:∵ 该函数图象的开口向下,∴ a<0;
∵ a<0,-b2a<0,
∴ b<0,
∵ 抛物线和y轴的交点是(0,?2),
∴ c>0,
∴ abc>0,故②正确;
∵ 二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,?2),
∴ a-b+c=2,故①正确;
根据图象知,当x=-2时,y<0,即4a-2b+c<0;故③正确;
∵ 对称轴-1∴ 2a-b<0,故④正确;
故答案为①②③④.
20.
【答案】
2
【解答】
解:根据表格给出的各点坐标可得出,该函数的对称轴为直线x=0,
求得函数解析式为y=3x2-1,
则x=2与x=-2时应取值相同,故这个算错的y值所对应的x=2.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:(1)∵ 二次函数y=ax2+4x+2的图象经过点A(3,?-4),
∴ 9a+12+2=-4,
∴ a=-2;
(2)∵ y=-2x2+4x+2=-2(x-1)2+4,
∴ 顶点坐标为(1,?4);
(3)∵ y=-2x2+4x+2中,a=-2<0,
抛物线开口向下,对称轴为直线x=1,
∴ 当x>1时,函数y随自变量增大而减小.
【解答】
解:(1)∵ 二次函数y=ax2+4x+2的图象经过点A(3,?-4),
∴ 9a+12+2=-4,
∴ a=-2;
(2)∵ y=-2x2+4x+2=-2(x-1)2+4,
∴ 顶点坐标为(1,?4);
(3)∵ y=-2x2+4x+2中,a=-2<0,
抛物线开口向下,对称轴为直线x=1,
∴ 当x>1时,函数y随自变量增大而减小.
22.
【答案】
【解答】
此题暂无解答
23.
【答案】
<.
【解答】
解:(1)∵ 抛物线y=ax2经过点A(-2,?4).
∴ 4=(-2)2a,
∴ a=1,
∴ 抛物线的函数关系式为
(2)∵ 当x=-3时,y=(-3)2=3,
∴ 点B(-3,?-3)不在此抛物线上.
(3)∵ 抛物线y=x2的对称轴为y轴,图象上有两点M(x1,?y1)、N(x2,?y2),其中|x1|<|x2|,
∴ M(x1,?y1)比N(x2,?y2)离y轴要近,
而抛物线开口向上,
∴ y124.
【答案】
解:(1)∵ 抛物线与y轴的交点在x轴下方,
∴ c<0;
(2)∵ 抛物线经过点(0,?-1),
∴ c=-1,
∴ 抛物线解析式为y=x2-2x-1.
【解答】
解:(1)∵ 抛物线与y轴的交点在x轴下方,
∴ c<0;
(2)∵ 抛物线经过点(0,?-1),
∴ c=-1,
∴ 抛物线解析式为y=x2-2x-1.
25.
【答案】
解:(1)解方程组y=x2-2,y=x+4,
解得:x1=3,y1=7,和x2=-2,y2=2,
即A的坐标为(-2,2),B的坐标为(3,7).
(2)当y1【解答】
解:(1)解方程组y=x2-2,y=x+4,
解得:x1=3,y1=7,和x2=-2,y2=2,
即A的坐标为(-2,2),B的坐标为(3,7).
(2)当y126.
【答案】
由题意得抛物线y=-x2+2bx+b2+1的对称轴为x=-2b-2=b,
∴ 点A坐标为(b,?0),
∴ 点B坐标为(0,?3-b2)
把(0,?2)代入y=-x2+2bx+b2+1中,
解得b=±1.
∵ b>0,
∴ b=1.
∴ 抛物线的表达式为y=-x2+2x+2;
当抛物线过点B时,抛物线AB有一个公共点,
∴ b2+1=3-b2
∴ b=±1,
如图:当b>1时,抛物线与线段AB无交点;
当b=1时,抛物线与线段AB有一个交点;
当-1当b=-1时,抛物线与线段AB有一个交点;
当b<-1时,抛物线与线段AB无交点.
∴ 若抛物线与线段AB恰有一个公共点,则-1≤b≤1.
【解答】
由题意得抛物线y=-x2+2bx+b2+1的对称轴为x=-2b-2=b,
∴ 点A坐标为(b,?0),
∴ 点B坐标为(0,?3-b2)
把(0,?2)代入y=-x2+2bx+b2+1中,
解得b=±1.
∵ b>0,
∴ b=1.
∴ 抛物线的表达式为y=-x2+2x+2;
当抛物线过点B时,抛物线AB有一个公共点,
∴ b2+1=3-b2
∴ b=±1,
如图:当b>1时,抛物线与线段AB无交点;
当b=1时,抛物线与线段AB有一个交点;
当-1当b=-1时,抛物线与线段AB有一个交点;
当b<-1时,抛物线与线段AB无交点.
∴ 若抛物线与线段AB恰有一个公共点,则-1≤b≤1.
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 将y=x2+6x+7化为y=a(x-h)2+k的形式,h,k的值分别为( )
A.3,-2 B.-3,-2 C.3,-16 D.-3,-16
?
2. 抛物线y=3x2,y=-3x2,y=13x2都有的性质是(? ? ? ? )
A.开口向下 B.对称轴是y轴
C.都有最低点 D.y随x的增大而减小
?3. 抛物线y=-2x2-12x-23的顶点坐标是(? ? ? ? )
A.3,-5 B.3,5 C.-3,-5 D.-3,5
?
4. 对于二次函数y=x2-2mx-3,有下列说法:
①它的图象与x轴有两个公共点;
②如果当x≤1时y随x的增大而减小,则m=1;
③如果将它的图象向左平移3个单位后过原点,则m=-1;
④如果当x=4时的函数值与x=2008时的函数值相等,则当x=2012时的函数值为-3.
其中正确的个数是( )
A.1 B.2 C.3 D.4
?
5. 已知抛物线y=ax2-2ax-1(a≠0),下列四个结论:①当a>0时,在对称轴的右边,y随x的增大而增大;②函数图象的对称轴是x=-1;③当a=1时,图象经过点(-1,?2);④当a=-2时,函数图象与x轴没有交点,其中正确的共有( )
A.4个 B.3个 C.2个 D.1个
?
6. 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,?0),有下列结论:
①abc>0;?②a-2b+4c=0;?③25a-10b+4c=0;?④3b+2c>0;⑤a-b≥m(am-b).
其中所有正确的结论是( )
A.①②③ B.①③④ C.①②③⑤ D.①③⑤
?
7. 如图,二次函数y=ax2+bx+c的图象经过点A(1,?0),B(5,?0),下列说法正确的是(? ? ? ? )
A.c<0 B.b2-4ac<0
C.a-b+c<0 D.图象的对称轴是直线x=3
?8. 二次函数y=ax2+bx+c的图象如图所示,则下列结论中正确的是( )
A.a>0??b<0??c>0 B.a<0??b<0??c>0
C.a<0??b>0??c<0 D.a<0??b>0??c>0
?
9. 抛物线y=-3(x-1)2+2的对称轴是( )
A.x=1 B.x=-1 C.x=2 D.x=-2
?
10. 如果点A(1,?3),B(m,?3)是抛物线y=a(x-4)2+h上两个不同的点,那么m的值为(? ? ? ? )
A.4 B.5 C.6 D.7
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 二次函数y=ax2+6x+a的最大值是8,则a=________.
?
12. 抛物线y=ax2+bx+c开口向上,对称轴是直线x=1,A(-2,?y1),B(0,?y2),C(2,?y3)在该抛物线上,则y1,y2,y3大小的关系是________.
?
13. 已知抛物线的顶点为(-1,?-3),与y轴的交点为(0,?-5),则此抛物线的解析式是________.
?
14. 二次函数y=-(x-1)2+8的最大值是________.
?
15. 用配方法把y=x2+2x+4化为y=a(x+h)2+k的形式为________.
?
16. 抛物线y=ax2+bx+c过点A(1,?0),B(3,?0),则此抛物线的对称轴是直线x=________.
?
17. 如果二次函数y=x2+bx+c配方后为y=(x-2)2+1,那么c的值为________.
?
18. 点A(2,?y1)、B(3,?y2)是二次函数y=-x2+2x+m的图象上两点,则y1与y2的大小关系为y1________?y2(填“>”、“<”、“=”).
?
19. 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,?2),且与x轴交点的横坐标分别为x1、x2,其中-2
其中正确的是________.
?
20. 小颖同学想用“描点法”画二次函数y=ax2+bx+c(a≠0)的图象,取自变量x的5个值,分别计算出对应的y值,如下表:
x
…
-2
-1
0
1
2
…
y
…
11
2
-1
2
5
…
由于粗心,小颖算错了其中的一个y值,请你指出这个算错的y值所对应的x=________.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 , ) ?
21. 已知二次函数y=ax2+4x+2的图象经过点A(3,?-4).
(1)求a的值;
(2)求此函数图象抛物线的顶点坐标;
(3)直接写出函数y随自变量增大而减小的x的取值范围.
?
22. 已知二次函数y=ax2+bx+c的图象C经过-5,0,0,52,1,6三点,直线l的解析式为y=2x-3.
(1)求抛物线C的解析式;
(2)判断抛物线C与直线l有无公共点;
(3)若与直线l平行的直线y=2x+m与抛物线C只有一个公共点P,求点P的坐标.
?
23. 已知抛物线y=ax2经过点A(-2,?4).
(1)求该抛物线的函数关系式;
(2)判断点B(-3,?-3)是否在此抛物线上;
(3)若图象上有两点M(x1,?y1)、N(x2,?y2),其中|x1|<|x2|,则y1________y2(在横线上填“<”“=”或“>”).
?
24. 已知二次函数y=x2-2x+c的部分图象如图所示.
(1)求c的取值范围;
(2)若抛物线经过点(0,?-1),试确定抛物线y=x2-2x+c的函数表达式.
?
25. 如图,抛物线 y1=x2-2 与直线 y2=x+4 交于A,B两点.
(1)求A,B两点的坐标;
(2)当 y1
26. 在平面直角坐标系xOy中,抛物线y=-x2+2bx+b2+1的对称轴与x轴交于点A,将点A向左平移b个单位,再向上平移3-b2个单位,得到点B.
(1)求点B的坐标(用含b的式子表示);
(2)当抛物线经过点(0,?2),且b>0时,求抛物线的表达式;
(3)若抛物线与线段AB恰有一个公共点,结合图象,直接写出b的取值范围.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
【解答】
解:∵ y=x2+6x+7=x2+6x+9-9+7=(x+3)2-2,
∴ h=-3,k=-2.
故选:B.
2.
【答案】
B
【解答】
解:在y=3x2中,可知其开口向上,对称轴为y轴,有最低点;
在y=-3x2中,可知其开口向下,对称轴为y轴,有最高点;
在y=13x2中,可知其开口向上,对称轴为y轴,有最低点;
∴ 三抛物线共有的性质是对称轴为y轴.
故选B.
3.
【答案】
C
【解答】
解:∵ y=-2x2-12x-23=-2x+32-5,
∴ 抛物线的顶点坐标为-3,-5.
故选C.
4.
【答案】
B
【解答】
解:①∵ △=(-2m)2-4×1×(-3)=4m2+12>0,
∴ 它的图象与x轴有两个公共点,故本小题正确;
②∵ 当x≤1时y随x的增大而减小,
∴ 对称轴直线x=--2m2×1≥1,
解得m≥1,故本小题错误;
③∵ 将它的图象向左平移3个单位后过原点,
∴ 平移前的图象经过点(3,?0),
代入函数关系式得,32-2m?3-3=0,
解得m=1,故本小题错误;
④∵ 当x=4时的函数值与x=2008时的函数值相等,
∴ 对称轴为直线x=4+20082=1006,
∴ --2m2×1=1006,
解得m=1006,
∴ 函数关系式为y=x2-2012x-3,
当x=2012时,y=20122-2012×2012-3=-3,故本小题正确;
综上所述,结论正确的是①④共2个.
故选B.
5.
【答案】
C
【解答】
∵ 抛物线y=ax2-2ax-1(a≠0),
∴ 当a>0时,抛物线开口向上,在对称轴的右边,y随x的增大而增大,故①正确,
函数图象的对称轴是直线x=--2a2a=1,故②错误,
当a=1时,y=x2-2x-1,当x=-1时,y=2,故③正确,
当a=-2时,y=-2x2+4x-1,当y=0时,-2x2+4x-1=0,则△=42-4×(-2)×(-1)=8>0,故当a=-2时,函数图象与x轴有两个交点,故④错误,
6.
【答案】
D
【解答】
由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴ abc>0,故①正确;
直线x=-1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以-b2a=-1,可得b=2a,
a-2b+4c=a-4a+4c=-3a+4c,
∵ a<0,
∴ -3a>0,
∴ -3a+4c>0,
即a-2b+4c>0,故②错误;
∵ 抛物线y=ax2+bx+c的对称轴是x=-1.且过点(12,?0),
∴ 抛物线与x轴的另一个交点坐标为(-52,?0),
当x=-52时,y=0,即a(-52)2-52b+c=0,
整理得:25a-10b+4c=0,故③正确;
∵ b=2a,a+b+c<0,
∴ 12b+b+c<0,
即3b+2c<0,故④错误;
当x=-1时,a-b+c≥am2-bm+c,
∴ a-b≥m(am-b),故⑤正确;
7.
【答案】
D
【解答】
解:A,由于二次函数y=ax2+bx+c的图象与y轴交于正半轴,所以c>0,故A错误;
B,二次函数y=ax2+bx+c的图象与x轴有2个交点,所以b2-4ac>0,故B错误;
C,当x=-1时,y>0,即a-b+c>0,故C错误;
D,因为A(1,?0),B(5,?0),所以对称轴为直线x=1+52=3,故D正确.
故选D.
8.
【答案】
D
【解答】
解:∵ 抛物线开口向下,
∴ a<0;
又∵ 抛物线的对称轴在y轴的右侧,
∴ x=-b2a>0,
∴ b>0,
而抛物线与y轴的交点在x轴上方,
∴ c>0.
故选D.
9.
【答案】
A
【解答】
令x-1=0,则x=1.
10.
【答案】
D
【解答】
解:点A(1,?3),B(m,?3)是抛物线y=a(x-4)2+h上两个不同的点,
得(1,?3)与(m,?3)关于对称轴x=4对称,
m-4=4-1,
解得m=7.
故选D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
-1
【解答】
解:
当a<0时,二次函数有最大值,其公式为ymax=4ac-b24a,
∴ 4a2-624a=8,整理可得a2-8a-9=0,
解得a=9(舍去)或a=-1,
故答案为:-1.
12.
【答案】
y1>y2=y3
【解答】
∵ 抛物线y=ax2+bx+c开口向上,对称轴是直线x=1,
∴ 抛物线上的点离对称轴越远,对应的函数值就越大,
∵ x取-2时所对应的点离对称轴最远,x取0与2时所对应的点离对称轴一样近,
∴ y1>y2=y3.
13.
【答案】
y=-2x2-4x-5
【解答】
解:根据题意设y=a(x+1)2-3,
将(0,?-5)代入得:a-3=-5,
解得:a=-2,
则抛物线解析式为y=-2(x+1)2-3=-2x2-4x-5.
故答案为:y=-2x2-4x-5
14.
【答案】
8
【解答】
∵ y=-(x-1)2+8,
∴ 此函数的顶点坐标是(1,?8),
即当x=1时,函数有最大值8.
15.
【答案】
y=(x+1)2+3
【解答】
y=x2+2x+4
=(x2+2x+1)+3
=(x+1)2+3,
即y=(x+1)2+3.
16.
【答案】
2
【解答】
解:∵ 点A(1,?0),B(3,?0)的纵坐标相等,
∴ A、B两点是抛物线上的两个对称点,
∴ 对称轴是直线x=1+32=2.
17.
【答案】
5
【解答】
∵ y=(x-2)2+1
=x2-4x+4+1
=x2-4x+5,
∴ c的值为5.
18.
【答案】
<
【解答】
解:∵ 二次函数y=x2+2x+m的图象的对称轴是x=-1,
在对称轴的右面y随x的增大而增大,
∵ 点A(2,?y1)、B(3,?y2)是二次函数y=x2+2x+m的图象上两点,
2<3,
∴ y1
19.
【答案】
①②③④
【解答】
解:∵ 该函数图象的开口向下,∴ a<0;
∵ a<0,-b2a<0,
∴ b<0,
∵ 抛物线和y轴的交点是(0,?2),
∴ c>0,
∴ abc>0,故②正确;
∵ 二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,?2),
∴ a-b+c=2,故①正确;
根据图象知,当x=-2时,y<0,即4a-2b+c<0;故③正确;
∵ 对称轴-1
故答案为①②③④.
20.
【答案】
2
【解答】
解:根据表格给出的各点坐标可得出,该函数的对称轴为直线x=0,
求得函数解析式为y=3x2-1,
则x=2与x=-2时应取值相同,故这个算错的y值所对应的x=2.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:(1)∵ 二次函数y=ax2+4x+2的图象经过点A(3,?-4),
∴ 9a+12+2=-4,
∴ a=-2;
(2)∵ y=-2x2+4x+2=-2(x-1)2+4,
∴ 顶点坐标为(1,?4);
(3)∵ y=-2x2+4x+2中,a=-2<0,
抛物线开口向下,对称轴为直线x=1,
∴ 当x>1时,函数y随自变量增大而减小.
【解答】
解:(1)∵ 二次函数y=ax2+4x+2的图象经过点A(3,?-4),
∴ 9a+12+2=-4,
∴ a=-2;
(2)∵ y=-2x2+4x+2=-2(x-1)2+4,
∴ 顶点坐标为(1,?4);
(3)∵ y=-2x2+4x+2中,a=-2<0,
抛物线开口向下,对称轴为直线x=1,
∴ 当x>1时,函数y随自变量增大而减小.
22.
【答案】
【解答】
此题暂无解答
23.
【答案】
<.
【解答】
解:(1)∵ 抛物线y=ax2经过点A(-2,?4).
∴ 4=(-2)2a,
∴ a=1,
∴ 抛物线的函数关系式为
(2)∵ 当x=-3时,y=(-3)2=3,
∴ 点B(-3,?-3)不在此抛物线上.
(3)∵ 抛物线y=x2的对称轴为y轴,图象上有两点M(x1,?y1)、N(x2,?y2),其中|x1|<|x2|,
∴ M(x1,?y1)比N(x2,?y2)离y轴要近,
而抛物线开口向上,
∴ y1
【答案】
解:(1)∵ 抛物线与y轴的交点在x轴下方,
∴ c<0;
(2)∵ 抛物线经过点(0,?-1),
∴ c=-1,
∴ 抛物线解析式为y=x2-2x-1.
【解答】
解:(1)∵ 抛物线与y轴的交点在x轴下方,
∴ c<0;
(2)∵ 抛物线经过点(0,?-1),
∴ c=-1,
∴ 抛物线解析式为y=x2-2x-1.
25.
【答案】
解:(1)解方程组y=x2-2,y=x+4,
解得:x1=3,y1=7,和x2=-2,y2=2,
即A的坐标为(-2,2),B的坐标为(3,7).
(2)当y1
解:(1)解方程组y=x2-2,y=x+4,
解得:x1=3,y1=7,和x2=-2,y2=2,
即A的坐标为(-2,2),B的坐标为(3,7).
(2)当y1
【答案】
由题意得抛物线y=-x2+2bx+b2+1的对称轴为x=-2b-2=b,
∴ 点A坐标为(b,?0),
∴ 点B坐标为(0,?3-b2)
把(0,?2)代入y=-x2+2bx+b2+1中,
解得b=±1.
∵ b>0,
∴ b=1.
∴ 抛物线的表达式为y=-x2+2x+2;
当抛物线过点B时,抛物线AB有一个公共点,
∴ b2+1=3-b2
∴ b=±1,
如图:当b>1时,抛物线与线段AB无交点;
当b=1时,抛物线与线段AB有一个交点;
当-1
当b<-1时,抛物线与线段AB无交点.
∴ 若抛物线与线段AB恰有一个公共点,则-1≤b≤1.
【解答】
由题意得抛物线y=-x2+2bx+b2+1的对称轴为x=-2b-2=b,
∴ 点A坐标为(b,?0),
∴ 点B坐标为(0,?3-b2)
把(0,?2)代入y=-x2+2bx+b2+1中,
解得b=±1.
∵ b>0,
∴ b=1.
∴ 抛物线的表达式为y=-x2+2x+2;
当抛物线过点B时,抛物线AB有一个公共点,
∴ b2+1=3-b2
∴ b=±1,
如图:当b>1时,抛物线与线段AB无交点;
当b=1时,抛物线与线段AB有一个交点;
当-1
当b<-1时,抛物线与线段AB无交点.
∴ 若抛物线与线段AB恰有一个公共点,则-1≤b≤1.
