人教版五年级数学下册3.5长方体和正方体的体积 教案
文档属性
| 名称 | 人教版五年级数学下册3.5长方体和正方体的体积 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 71.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 14:51:26 | ||
图片预览

文档简介
第5课时 长方体和正方体的体积
【教学内容】
教材第29~30页内容。
【教学目标】
1.理解长方体、正方体体积公式的推导过程,掌握其计算方法。
2.经历长方体和正方体体积计算公式的探究过程,发展学生的空间观念。
3.学会解决实际生活中有关长方体和正方体体积的计算问题。
4.激发学生的学习兴趣,体验成功的喜悦,培养学生合作探究的能力。
【教学重点】
理解并掌握长方体和正方体的体积计算方法。
【教学难点】
理解长方体体积计算公式的推导过程。
一、复习导入
师:同学们,什么叫做体积?
生:物体所占空间的大小叫做物体的体积。
师:常用的体积单位有哪些?你能举例或者用手势来表示它们的大小吗?
生:立方米、立方分米和立方厘米。(手势略)
二、探究新知
1.长方体体积的计算。
教师课件出示一块长方体积木,一块盖房用的大型砖板。
(1)提问:它们的体积是多少?你是怎样想的?
引导学生回答:长方体积木的体积可以用1立方厘米的正方体去摆,有几个1立方厘米的正方体,它的体积就是多少立方厘米,但是相对于大型砖板再用1 cm3或1 dm3去量就比较麻烦。
师:请同学们想一想,如果要知道较大物体的体积,我们能不能用学过的数学知识来计算。
(2)观察操作,探究长方体的体积公式。
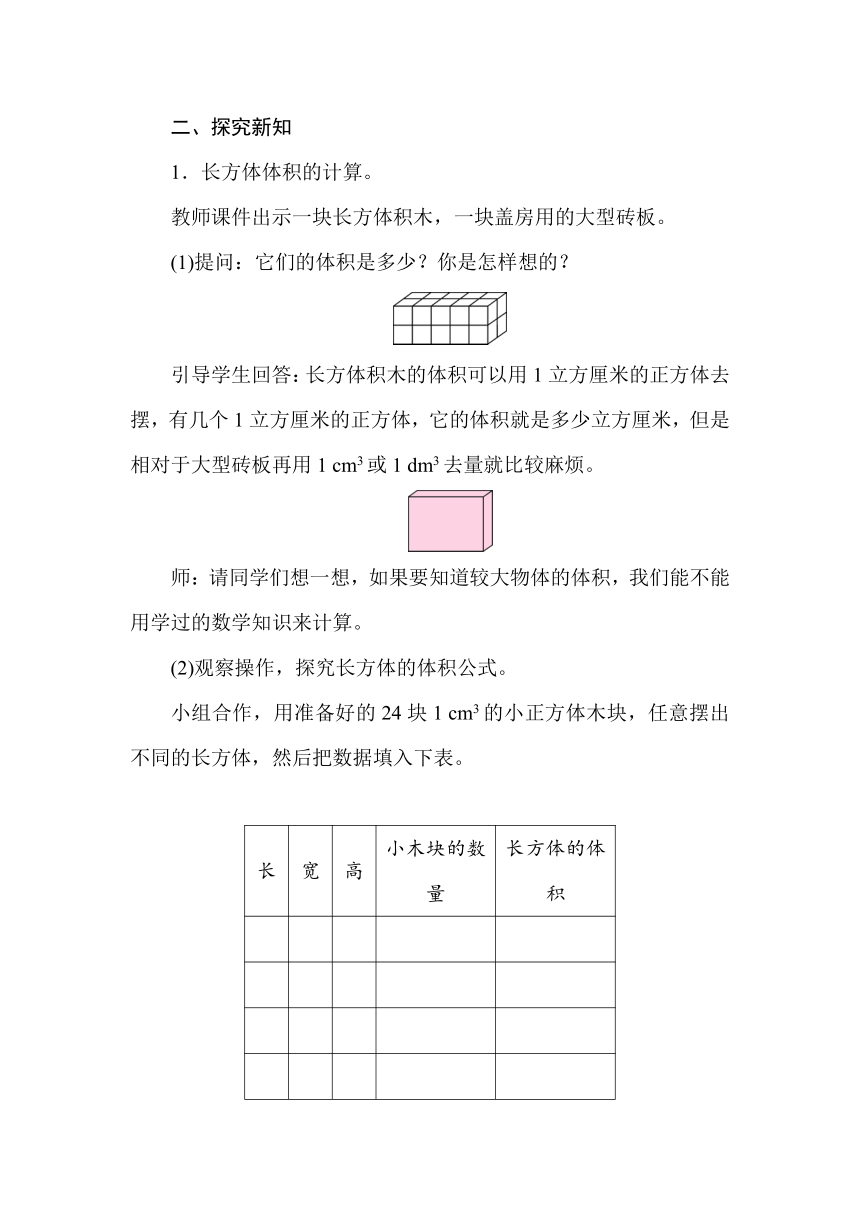
小组合作,用准备好的24块1 cm3的小正方体木块,任意摆出不同的长方体,然后把数据填入下表。
长 宽 高 小木块的数量 长方体的体积
学生拼摆,然后填表,集体汇报,老师把有代表性的数字写在表中。
长 宽 高 小木块的数量 长方体的体积
8 3 1 24 24
4 3 2 24 24
3 2 4 24 24
2 3 4 24 24
说明学生拼摆长方体的样式非常多,这里只列举几个。观察:从这张表中,你发现了什么?
学生独立思考,然后小组内讨论交流,得出结论。
小结:长方体的体积等于长方体所含体积单位的数量,所含体积单位的数量正好等于长方体长、宽、高的乘积。
板书:长方体的体积=长×宽×高。
讲述:如果用字母V表示长方体的体积,那么其体积公式可以写成:V=abh。
(3)利用公式计算长方体的体积。
出示例1的长方体图形。
学生独立完成。
生1:根据V=abh=7×3×4=84(cm3)。
生2:这个长方体的长表示每一排有7个1 cm3的小正方体,宽表示摆了这样的3排,高表示摆了4层,所以它的体积V=7×3×4=84(cm3)。
2.迁移类推,归纳正方体体积的计算公式。
(1)教师出示电脑动画,由长方体转变成正方体。
师:大家想一想,正方体的体积要怎样计算呢?
生1:正方体是特殊的长方体,所以也应该和长方体一样用长×宽×高表示。
师:和长方体的计算方法一样?
生2:我也认为和长方体的计算方法一样。但是正方体的长、宽、高都相等,所以应该表示为棱长×棱长×棱长。
教师引导学生小结,板书:
正方体的体积=棱长×棱长×棱长
师:我们还是用V表示正方体的体积,a表示棱长,所以字母公式可以写成V=a·a·a,也可以写成V=a3,读作“a的立方”,表示三个a相乘,在写a3时,3要写在a的右上角。
(2)应用公式解决实际问题。
出示例1的正方体图形。
学生独立完成,集体交流。
教师板书:V=a3=6×6×6=216(dm3)
三、巩固练习
1.教材第31页“做一做”第1、2题。
2.教材第32~33页“练习七”的第6、8题。
四、课堂小结
1.这节课,你有什么收获?
2.在计算长方体和正方体的体积时,要注意哪些问题?
【板书设计】
长方体和正方体的体积
公式:长方体的体积=长×宽×高 V=abh
V=abh=7×3×4=84(cm3)
公式:正方体的体积=棱长×棱长×棱长
V=a3
V=a3=6×6×6=216(dm3)
【教后思考】
1.复习体积和体积单位,巩固学生头脑中已形成的表象,设计求大型砖板体积的环节,让学生根据已有的经验猜一猜,明确研究的方向。
2.学生在课堂学习中总是渴望自己是知识的发现者,因为他需要以此来获取成功的体验,从而得到老师和同学的赞扬。
3.通过学生的操作实践活动,使学生亲历“做数学”的过程,积累数学活动的经验,发展学生的空间概念和推理能力。
【教学内容】
教材第29~30页内容。
【教学目标】
1.理解长方体、正方体体积公式的推导过程,掌握其计算方法。
2.经历长方体和正方体体积计算公式的探究过程,发展学生的空间观念。
3.学会解决实际生活中有关长方体和正方体体积的计算问题。
4.激发学生的学习兴趣,体验成功的喜悦,培养学生合作探究的能力。
【教学重点】
理解并掌握长方体和正方体的体积计算方法。
【教学难点】
理解长方体体积计算公式的推导过程。
一、复习导入
师:同学们,什么叫做体积?
生:物体所占空间的大小叫做物体的体积。
师:常用的体积单位有哪些?你能举例或者用手势来表示它们的大小吗?
生:立方米、立方分米和立方厘米。(手势略)
二、探究新知
1.长方体体积的计算。
教师课件出示一块长方体积木,一块盖房用的大型砖板。
(1)提问:它们的体积是多少?你是怎样想的?
引导学生回答:长方体积木的体积可以用1立方厘米的正方体去摆,有几个1立方厘米的正方体,它的体积就是多少立方厘米,但是相对于大型砖板再用1 cm3或1 dm3去量就比较麻烦。
师:请同学们想一想,如果要知道较大物体的体积,我们能不能用学过的数学知识来计算。
(2)观察操作,探究长方体的体积公式。
小组合作,用准备好的24块1 cm3的小正方体木块,任意摆出不同的长方体,然后把数据填入下表。
长 宽 高 小木块的数量 长方体的体积
学生拼摆,然后填表,集体汇报,老师把有代表性的数字写在表中。
长 宽 高 小木块的数量 长方体的体积
8 3 1 24 24
4 3 2 24 24
3 2 4 24 24
2 3 4 24 24
说明学生拼摆长方体的样式非常多,这里只列举几个。观察:从这张表中,你发现了什么?
学生独立思考,然后小组内讨论交流,得出结论。
小结:长方体的体积等于长方体所含体积单位的数量,所含体积单位的数量正好等于长方体长、宽、高的乘积。
板书:长方体的体积=长×宽×高。
讲述:如果用字母V表示长方体的体积,那么其体积公式可以写成:V=abh。
(3)利用公式计算长方体的体积。
出示例1的长方体图形。
学生独立完成。
生1:根据V=abh=7×3×4=84(cm3)。
生2:这个长方体的长表示每一排有7个1 cm3的小正方体,宽表示摆了这样的3排,高表示摆了4层,所以它的体积V=7×3×4=84(cm3)。
2.迁移类推,归纳正方体体积的计算公式。
(1)教师出示电脑动画,由长方体转变成正方体。
师:大家想一想,正方体的体积要怎样计算呢?
生1:正方体是特殊的长方体,所以也应该和长方体一样用长×宽×高表示。
师:和长方体的计算方法一样?
生2:我也认为和长方体的计算方法一样。但是正方体的长、宽、高都相等,所以应该表示为棱长×棱长×棱长。
教师引导学生小结,板书:
正方体的体积=棱长×棱长×棱长
师:我们还是用V表示正方体的体积,a表示棱长,所以字母公式可以写成V=a·a·a,也可以写成V=a3,读作“a的立方”,表示三个a相乘,在写a3时,3要写在a的右上角。
(2)应用公式解决实际问题。
出示例1的正方体图形。
学生独立完成,集体交流。
教师板书:V=a3=6×6×6=216(dm3)
三、巩固练习
1.教材第31页“做一做”第1、2题。
2.教材第32~33页“练习七”的第6、8题。
四、课堂小结
1.这节课,你有什么收获?
2.在计算长方体和正方体的体积时,要注意哪些问题?
【板书设计】
长方体和正方体的体积
公式:长方体的体积=长×宽×高 V=abh
V=abh=7×3×4=84(cm3)
公式:正方体的体积=棱长×棱长×棱长
V=a3
V=a3=6×6×6=216(dm3)
【教后思考】
1.复习体积和体积单位,巩固学生头脑中已形成的表象,设计求大型砖板体积的环节,让学生根据已有的经验猜一猜,明确研究的方向。
2.学生在课堂学习中总是渴望自己是知识的发现者,因为他需要以此来获取成功的体验,从而得到老师和同学的赞扬。
3.通过学生的操作实践活动,使学生亲历“做数学”的过程,积累数学活动的经验,发展学生的空间概念和推理能力。
