4二次函数的应用(第1课时) 课件(共16张PPT)
文档属性
| 名称 | 4二次函数的应用(第1课时) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 979.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览






文档简介
同学们在路边、闹市区经常会看到很多的大型广告牌,大家平常见到的广告牌一般什么形状的比较多?
思考下面的问题:
现在一个广告公司接到了一笔业务,需要设计一块周长为12 m的矩形广告牌,由于公司一般根据广告牌面积的大小收取制作设计费,如果你是该公司的设计员,你能否设计出令广告公司老总满意的广告牌?
第二章 二次函数
2.4 二次函数的应用
(第1课时)
1.经历计算最大面积问题的探究,体会二次函数是一类最优化问题的数学模型,感受数学的应用价值.
2.能够分析和表示实际问题中变量间的函数关系,并运用二次函数知识解决实际问题的最值,增强解决问题的能力.
学习目标
探究活动一
如图所示,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
(1)如果设矩形的一边AB=x m,那么AD边的长度如何表示?
(2)设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少?
思考下面的问题:
1.△EBC和△EAF有什么关系?
2.如果设矩形的一边AB=x m,那么AD边的长度如何表示?
3.如何表示矩形ABCD的面积?
4.若矩形的面积为y m2,如何确定矩形ABCD面积的最大值?
解:(1)∵AB=x,∴CD=AB=x.
∵BC∥AD,∴△EBC∽△EAF.
又AB=x,∴BE=40-x,
(2)由矩形面积公式,得y=AB·AD=
所以当x=20时,y的值最大,最大值是300.
即当AB边长为20 m时,矩形ABCD的面积最大,是300 m2.
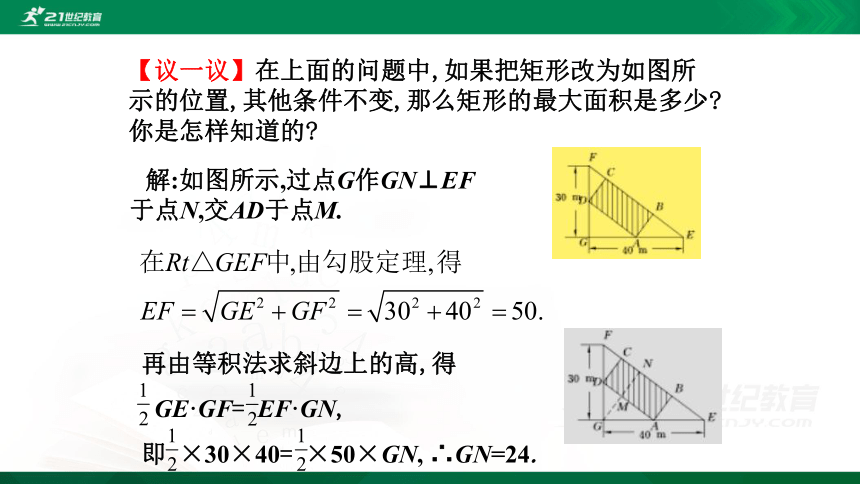
【议一议】在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
解:如图所示,过点G作GN⊥EF于点N,交AD于点M.
再由等积法求斜边上的高,得
GE·GF= EF·GN,
即 ×30×40= ×50×GN, ∴GN=24.
设矩形的一边AD=x m,由△GAD∽△GEF,
例2.在矩形ABCD中,AB=6 ,BC=12 ,点P从点A出发沿AB边向点B以1 /秒的速度移动,同时,点Q从点B出发沿BC边向点C以2 /秒的速度移动。如果P、Q两点在分别到达B、C两点后就
停止移动,设运动时间为t秒(0 (1)运动开始后第几秒时,△PBQ的面积等于8 ;
(2)设五边形APQCD的面积为S ,
写出S与t的函数关系式,t为何值时
S最小?求出S的最小值。
Q
P
C
B
A
D
Q
P
C
B
A
D
解:
(1)由题意得:
解得:
运动开始后2秒或4秒时,△PBQ的面积等于8 .
(2)由题意得:
当 时,
即 时, 有最小值,最小值为63
“二次函数应用” 的思路
1.理解问题;
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.运用数学知识求解;
5.检验结果的合理性,
给出问题的解答.
构建二次函数模型
归纳总结
1.已知二次函数y=3x2-12x+13,则函数值y的最小值是( )
A.3 B.2 C.1 D.-1
解析:∵二次函数y=3x2-12x+13可化为y=3(x-2)2+1,
∴当x=2时,二次函数y=3x2-12x+13有最小值,为1.故选C.
C
2.用长为8 m的铝合金制成的形状为矩形的窗框,则窗框的透光面积最大为 ( )
A. m2 B. m2 C. m2 D.4 m2
解析:设矩形的一边长为x m,则另一边长为(4-x)m,矩形的面积S=x(4-x)=-(x-2)2+4,因为a=-1<0,所以当x=2时,S有最大值,最大值为4.故选D.
D
随堂练习
3.周长为16 cm的矩形的最大面积为 cm2.?
16
4.如图所示,一边靠墙(墙足够长),用120 m篱笆围成两间相等的矩形鸡舍,要使鸡舍的总面积最大,则每间鸡舍的长与宽分别是 m, m.?
解析:由题意,得2x+3y=120,
所以y=40- x,
鸡舍的总面积S=2x = ,
所以当x=30时,鸡舍的总面积最大,此时y=20.
30
20
解:∵∠C=90°, AC=8, BC=6,
∴AB=10.
∵四边形CDEF是矩形,
∴EF∥AC, ∴△BEF∽△BAC,
5.一块三角形废料如图所示,∠C=90°,AC=8,BC=6.用这块废料剪出一个矩形CDEF,其中,点D,E,F分别在AC,AB,BC上.当AE为多长时所剪出的矩形CDEF面积最大?最大面积是多少?
同理可得DE= x.
矩形CDEF的面积
S=DE·EF= (0∴当x=5时, S有最大值,为12.
即当AE为5时, 所剪出的矩形CDEF面积最大, 最大面积为12.
设AE=x,则BE=10-x,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
思考下面的问题:
现在一个广告公司接到了一笔业务,需要设计一块周长为12 m的矩形广告牌,由于公司一般根据广告牌面积的大小收取制作设计费,如果你是该公司的设计员,你能否设计出令广告公司老总满意的广告牌?
第二章 二次函数
2.4 二次函数的应用
(第1课时)
1.经历计算最大面积问题的探究,体会二次函数是一类最优化问题的数学模型,感受数学的应用价值.
2.能够分析和表示实际问题中变量间的函数关系,并运用二次函数知识解决实际问题的最值,增强解决问题的能力.
学习目标
探究活动一
如图所示,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
(1)如果设矩形的一边AB=x m,那么AD边的长度如何表示?
(2)设矩形的面积为y m2,当x取何值时,y的值最大?最大值是多少?
思考下面的问题:
1.△EBC和△EAF有什么关系?
2.如果设矩形的一边AB=x m,那么AD边的长度如何表示?
3.如何表示矩形ABCD的面积?
4.若矩形的面积为y m2,如何确定矩形ABCD面积的最大值?
解:(1)∵AB=x,∴CD=AB=x.
∵BC∥AD,∴△EBC∽△EAF.
又AB=x,∴BE=40-x,
(2)由矩形面积公式,得y=AB·AD=
所以当x=20时,y的值最大,最大值是300.
即当AB边长为20 m时,矩形ABCD的面积最大,是300 m2.
【议一议】在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
解:如图所示,过点G作GN⊥EF于点N,交AD于点M.
再由等积法求斜边上的高,得
GE·GF= EF·GN,
即 ×30×40= ×50×GN, ∴GN=24.
设矩形的一边AD=x m,由△GAD∽△GEF,
例2.在矩形ABCD中,AB=6 ,BC=12 ,点P从点A出发沿AB边向点B以1 /秒的速度移动,同时,点Q从点B出发沿BC边向点C以2 /秒的速度移动。如果P、Q两点在分别到达B、C两点后就
停止移动,设运动时间为t秒(0
(2)设五边形APQCD的面积为S ,
写出S与t的函数关系式,t为何值时
S最小?求出S的最小值。
Q
P
C
B
A
D
Q
P
C
B
A
D
解:
(1)由题意得:
解得:
运动开始后2秒或4秒时,△PBQ的面积等于8 .
(2)由题意得:
当 时,
即 时, 有最小值,最小值为63
“二次函数应用” 的思路
1.理解问题;
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.运用数学知识求解;
5.检验结果的合理性,
给出问题的解答.
构建二次函数模型
归纳总结
1.已知二次函数y=3x2-12x+13,则函数值y的最小值是( )
A.3 B.2 C.1 D.-1
解析:∵二次函数y=3x2-12x+13可化为y=3(x-2)2+1,
∴当x=2时,二次函数y=3x2-12x+13有最小值,为1.故选C.
C
2.用长为8 m的铝合金制成的形状为矩形的窗框,则窗框的透光面积最大为 ( )
A. m2 B. m2 C. m2 D.4 m2
解析:设矩形的一边长为x m,则另一边长为(4-x)m,矩形的面积S=x(4-x)=-(x-2)2+4,因为a=-1<0,所以当x=2时,S有最大值,最大值为4.故选D.
D
随堂练习
3.周长为16 cm的矩形的最大面积为 cm2.?
16
4.如图所示,一边靠墙(墙足够长),用120 m篱笆围成两间相等的矩形鸡舍,要使鸡舍的总面积最大,则每间鸡舍的长与宽分别是 m, m.?
解析:由题意,得2x+3y=120,
所以y=40- x,
鸡舍的总面积S=2x = ,
所以当x=30时,鸡舍的总面积最大,此时y=20.
30
20
解:∵∠C=90°, AC=8, BC=6,
∴AB=10.
∵四边形CDEF是矩形,
∴EF∥AC, ∴△BEF∽△BAC,
5.一块三角形废料如图所示,∠C=90°,AC=8,BC=6.用这块废料剪出一个矩形CDEF,其中,点D,E,F分别在AC,AB,BC上.当AE为多长时所剪出的矩形CDEF面积最大?最大面积是多少?
同理可得DE= x.
矩形CDEF的面积
S=DE·EF= (0
即当AE为5时, 所剪出的矩形CDEF面积最大, 最大面积为12.
设AE=x,则BE=10-x,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
