北师大 版九年级数学上学期同步练习 1.2 矩形的性质与判定(word版含答案)
文档属性
| 名称 | 北师大 版九年级数学上学期同步练习 1.2 矩形的性质与判定(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览



文档简介
1.2
矩形的性质与判定
一.选择题
1.如图,矩形ABCD的对角线相交于点O,过点O作OG⊥AC,交AB于点G,连接CG,若∠BOG=15°,则∠BCG的度数是( )
A.15°
B.15.5°
C.20°
D.37.5°
2.在?ABCD中,E、F分别是AB、CD的中点,连接AF、CE.连接AC,当CA=CB时,判断四边形AECF是( )
A.平行四边形
B.矩形
C.菱形
D.正方形
3.如图,延长矩形ABCD的边BC至点E,使CE=CA,连接AE,如果∠ACB=38°,则∠E的值是( )
A.18°
B.19°
C.20°
D.40°
4.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为( )
A.60°
B.75°
C.72°
D.90°
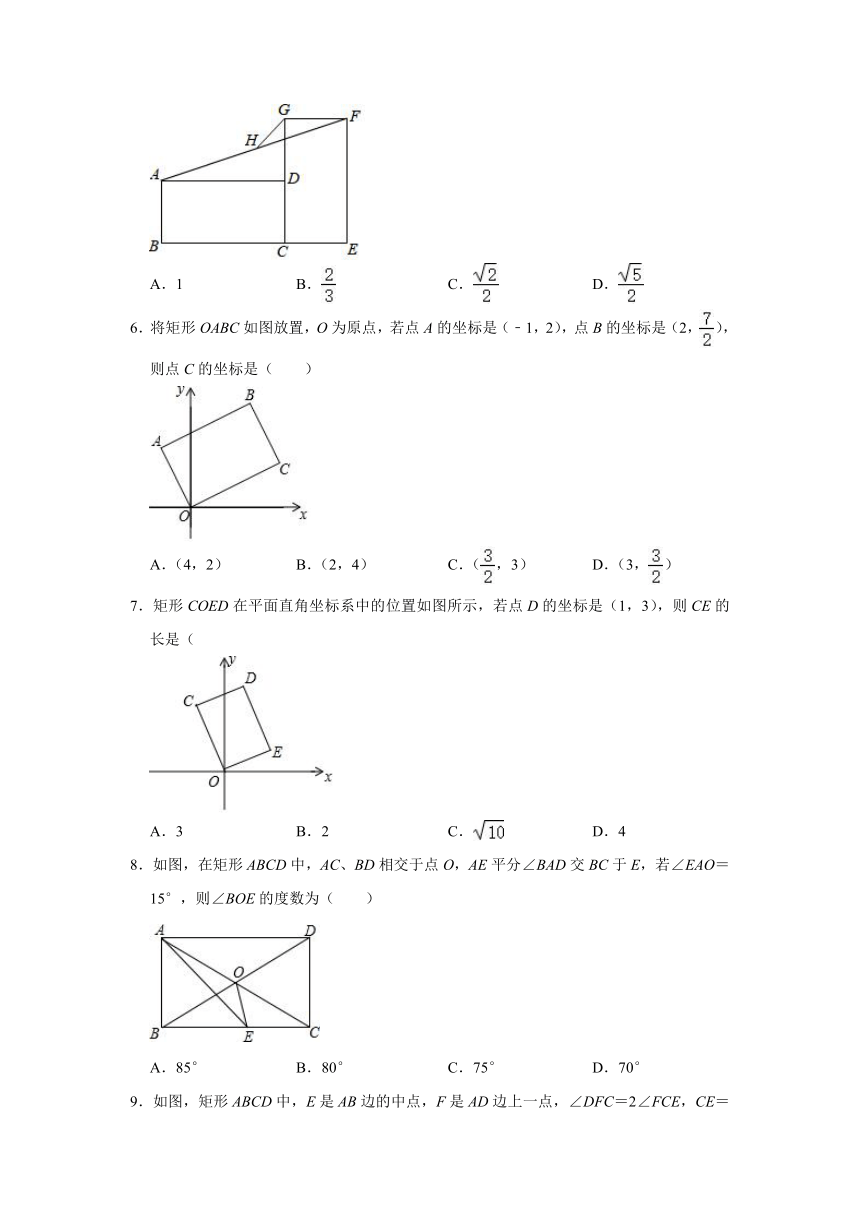
5.矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )
A.1
B.
C.
D.
6.将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,),则点C的坐标是( )
A.(4,2)
B.(2,4)
C.(,3)
D.(3,)
7.矩形COED在平面直角坐标系中的位置如图所示,若点D的坐标是(1,3),则CE的长是(
A.3
B.2
C.
D.4
8.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )
A.85°
B.80°
C.75°
D.70°
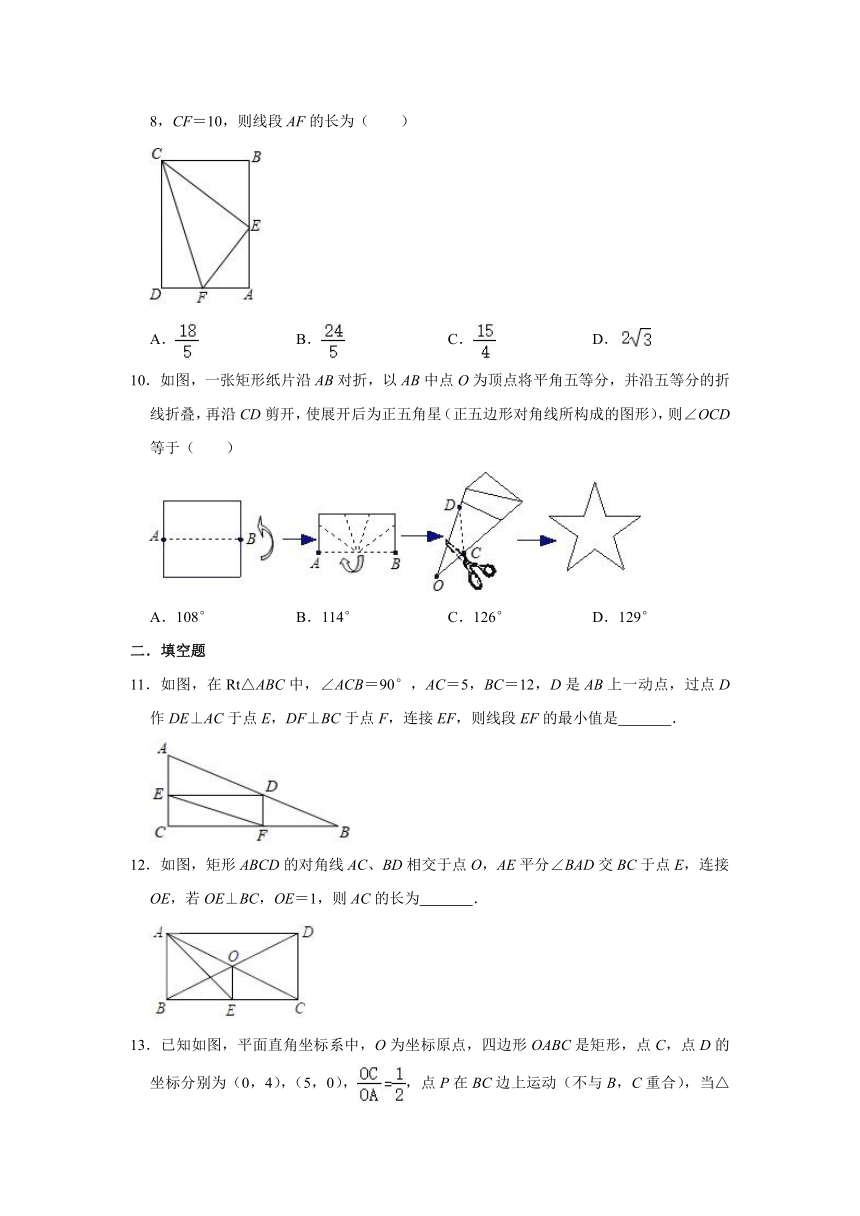
9.如图,矩形ABCD中,E是AB边的中点,F是AD边上一点,∠DFC=2∠FCE,CE=8,CF=10,则线段AF的长为( )
A.
B.
C.
D.
10.如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( )
A.108°
B.114°
C.126°
D.129°
二.填空题
11.如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是
.
12.如图,矩形ABCD的对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,连接OE,若OE⊥BC,OE=1,则AC的长为
.
13.已知如图,平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点C,点D的坐标分别为(0,4),(5,0),,点P在BC边上运动(不与B,C重合),当△ODP是腰长为5的等腰三角形时,点P的坐标为:
.
14.如图,矩形ABCD中,对角线AC、BD相交于O,∠AOB=60°,若BD=4,则AD=
.
三.解答题
15.如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是矩形;
(2)若E、F、G、H分别是OA、OB、OC、OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.
16.在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE=
,EF=
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
17.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)连接BF,求证:四边形BCAF是矩形.
18.已知:如图,在矩形ABCD中,E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.
(1)求证:BE=CD;
(2)若AB=4,AD=7,求△EFD的周长.
19.如图,点E,F分别在矩形ABCD的边AB,CD上,且∠DAF=∠BCE.
(1)求证:AF=CE;
(2)连接AC,若AC平分∠FAE,∠DAF=30°,CE=4,求CD的长.
参考答案
一.选择题
1.
A.
2.B.
3.
B.
4.
B.
5.
C.
6.
D.
7.
C.
8.
C.
9.
A.
10.
C.
二.填空题
11.
.
12.
2.
13.(2,4)或(3,4)或(8,4).
14.
2.
三.解答题
15.(1)证明:∵四边形ABCD是矩形,
∴OA=0B=OC=OD,
∵AE=BF=CG=DH,
∴AO﹣AE=OB﹣BF=CO﹣CG=DO﹣DH,
即:OE=OF=OG=OH,
∴四边形EFGH是矩形;
(2)解:∵G是OC的中点,
∴GO=GC,
∵DG⊥AC,
∴∠DGO=∠DGC=90°,
又∵DG=DG,
∴△DGC≌△DGO,
∴CD=OD,
∵F是BO中点,OF=2cm,
∴BO=4cm,
∵四边形ABCD是矩形,
∴DO=BO=4cm,
∴DC=4cm,DB=8cm,
∴CB==4,
∴矩形ABCD的面积=4×4=16cm2.
16.(1)解:∵四边形ABCD是矩形,
∴∠B=90°,
∴AC===5,
由题意得:AE=CF=t,
∴EF相遇前为:EF=AC﹣AE﹣CF=5﹣2t;
EF相遇后为:EF=AE+CF﹣AC=2t﹣5;
故答案为:t,5﹣2t或2t﹣5;
(2)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC===5,∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(3)解:如图所示,连接GH,
由(1)可知四边形EGFH是平行四边形
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5﹣2t=4,
解得:t=0.5.
②AE=CF=t,EF=5﹣2(5﹣t)=4,
解得:t=4.5
即:当t为0.5秒或4.5时,四边形EGFH为矩形
17.(1)证明:∵∠ACB=90°,∠CAB=30°,
∴BC=AB,∠ABC=60°,
∵△ABD是等边三角形,
∴∠ABD=∠BAD=60°,AB=AD,
∴∠ABC=∠BAD,
∴BC∥DA,
∵点E是线段AB的中点,
∴CE=AB=BE=AE,
∵∠ABC=60°,
∴△BCE是等边三角形,
∴∠BEC=60°=∠ABD,
∴BD∥CF,
∴四边形BCFD为平行四边形;
(2)证明:如图所示:
∵BD∥CF,BE=AE,
∴AF=DF=AD,
∴BC=AF,
又∵BC∥DA,
∴四边形BCAF是平行四边形,
∵∠ACB=90°,
∴四边形BCAF是矩形.
18.(1)证明:矩形ABCD中,∠B=∠C=90°,
∴∠1+∠3=90°,
∵EF⊥ED,
∴∠1+∠2=90°,
∴∠3=∠2,又EF=ED,
∴△BFE≌△CED,
∴BE=CD;
(2)解:矩形ABCD中,AB=CD=4,BC=AD=7,
∵△BFE≌△CED,
∴BE=CD=4,
∴EC=3,
∴ED=5,
∴EF=ED=5,
∴FD=,
∴△EFD的周长=.
19.(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠B=90°,
∵∠DAF=∠BCE,
∴△DAF≌△BCE(ASA),
∴AF=CE;
(2)解:如图,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CAB=∠DCA,
∵CE=4,
∴AF=4,
∵AC平分∠FAE,
∴∠FAC=∠CAB,
∴∠FAC=∠DCA,
∴FC=AF=4,
在Rt△ADF中,∠DAF=30°,
∴DF=2,
∴CD=6.
矩形的性质与判定
一.选择题
1.如图,矩形ABCD的对角线相交于点O,过点O作OG⊥AC,交AB于点G,连接CG,若∠BOG=15°,则∠BCG的度数是( )
A.15°
B.15.5°
C.20°
D.37.5°
2.在?ABCD中,E、F分别是AB、CD的中点,连接AF、CE.连接AC,当CA=CB时,判断四边形AECF是( )
A.平行四边形
B.矩形
C.菱形
D.正方形
3.如图,延长矩形ABCD的边BC至点E,使CE=CA,连接AE,如果∠ACB=38°,则∠E的值是( )
A.18°
B.19°
C.20°
D.40°
4.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE的度数为( )
A.60°
B.75°
C.72°
D.90°
5.矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )
A.1
B.
C.
D.
6.将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,),则点C的坐标是( )
A.(4,2)
B.(2,4)
C.(,3)
D.(3,)
7.矩形COED在平面直角坐标系中的位置如图所示,若点D的坐标是(1,3),则CE的长是(
A.3
B.2
C.
D.4
8.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )
A.85°
B.80°
C.75°
D.70°
9.如图,矩形ABCD中,E是AB边的中点,F是AD边上一点,∠DFC=2∠FCE,CE=8,CF=10,则线段AF的长为( )
A.
B.
C.
D.
10.如图,一张矩形纸片沿AB对折,以AB中点O为顶点将平角五等分,并沿五等分的折线折叠,再沿CD剪开,使展开后为正五角星(正五边形对角线所构成的图形),则∠OCD等于( )
A.108°
B.114°
C.126°
D.129°
二.填空题
11.如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是
.
12.如图,矩形ABCD的对角线AC、BD相交于点O,AE平分∠BAD交BC于点E,连接OE,若OE⊥BC,OE=1,则AC的长为
.
13.已知如图,平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点C,点D的坐标分别为(0,4),(5,0),,点P在BC边上运动(不与B,C重合),当△ODP是腰长为5的等腰三角形时,点P的坐标为:
.
14.如图,矩形ABCD中,对角线AC、BD相交于O,∠AOB=60°,若BD=4,则AD=
.
三.解答题
15.如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是矩形;
(2)若E、F、G、H分别是OA、OB、OC、OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.
16.在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE=
,EF=
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
17.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)连接BF,求证:四边形BCAF是矩形.
18.已知:如图,在矩形ABCD中,E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.
(1)求证:BE=CD;
(2)若AB=4,AD=7,求△EFD的周长.
19.如图,点E,F分别在矩形ABCD的边AB,CD上,且∠DAF=∠BCE.
(1)求证:AF=CE;
(2)连接AC,若AC平分∠FAE,∠DAF=30°,CE=4,求CD的长.
参考答案
一.选择题
1.
A.
2.B.
3.
B.
4.
B.
5.
C.
6.
D.
7.
C.
8.
C.
9.
A.
10.
C.
二.填空题
11.
.
12.
2.
13.(2,4)或(3,4)或(8,4).
14.
2.
三.解答题
15.(1)证明:∵四边形ABCD是矩形,
∴OA=0B=OC=OD,
∵AE=BF=CG=DH,
∴AO﹣AE=OB﹣BF=CO﹣CG=DO﹣DH,
即:OE=OF=OG=OH,
∴四边形EFGH是矩形;
(2)解:∵G是OC的中点,
∴GO=GC,
∵DG⊥AC,
∴∠DGO=∠DGC=90°,
又∵DG=DG,
∴△DGC≌△DGO,
∴CD=OD,
∵F是BO中点,OF=2cm,
∴BO=4cm,
∵四边形ABCD是矩形,
∴DO=BO=4cm,
∴DC=4cm,DB=8cm,
∴CB==4,
∴矩形ABCD的面积=4×4=16cm2.
16.(1)解:∵四边形ABCD是矩形,
∴∠B=90°,
∴AC===5,
由题意得:AE=CF=t,
∴EF相遇前为:EF=AC﹣AE﹣CF=5﹣2t;
EF相遇后为:EF=AE+CF﹣AC=2t﹣5;
故答案为:t,5﹣2t或2t﹣5;
(2)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC===5,∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(3)解:如图所示,连接GH,
由(1)可知四边形EGFH是平行四边形
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5﹣2t=4,
解得:t=0.5.
②AE=CF=t,EF=5﹣2(5﹣t)=4,
解得:t=4.5
即:当t为0.5秒或4.5时,四边形EGFH为矩形
17.(1)证明:∵∠ACB=90°,∠CAB=30°,
∴BC=AB,∠ABC=60°,
∵△ABD是等边三角形,
∴∠ABD=∠BAD=60°,AB=AD,
∴∠ABC=∠BAD,
∴BC∥DA,
∵点E是线段AB的中点,
∴CE=AB=BE=AE,
∵∠ABC=60°,
∴△BCE是等边三角形,
∴∠BEC=60°=∠ABD,
∴BD∥CF,
∴四边形BCFD为平行四边形;
(2)证明:如图所示:
∵BD∥CF,BE=AE,
∴AF=DF=AD,
∴BC=AF,
又∵BC∥DA,
∴四边形BCAF是平行四边形,
∵∠ACB=90°,
∴四边形BCAF是矩形.
18.(1)证明:矩形ABCD中,∠B=∠C=90°,
∴∠1+∠3=90°,
∵EF⊥ED,
∴∠1+∠2=90°,
∴∠3=∠2,又EF=ED,
∴△BFE≌△CED,
∴BE=CD;
(2)解:矩形ABCD中,AB=CD=4,BC=AD=7,
∵△BFE≌△CED,
∴BE=CD=4,
∴EC=3,
∴ED=5,
∴EF=ED=5,
∴FD=,
∴△EFD的周长=.
19.(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠B=90°,
∵∠DAF=∠BCE,
∴△DAF≌△BCE(ASA),
∴AF=CE;
(2)解:如图,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CAB=∠DCA,
∵CE=4,
∴AF=4,
∵AC平分∠FAE,
∴∠FAC=∠CAB,
∴∠FAC=∠DCA,
∴FC=AF=4,
在Rt△ADF中,∠DAF=30°,
∴DF=2,
∴CD=6.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
