人教版数学七年级上册3.4.1实际问题与一元一次方程-------工程问题教案
文档属性
| 名称 | 人教版数学七年级上册3.4.1实际问题与一元一次方程-------工程问题教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览



文档简介
第三章3.4《实际问题与一元一次方程》
-----工程问题
【教材】人教版数学
七年级
第三章
实际问题与一元一次方程。
【课时安排】第2课时。
【教学对象】七年级学生。
【教材分析】本节内容是学生在学习了代数式、简易方程及一元一次方程解法的基础上。对前一部分知识的应用与巩固,结合列方程解应用题的基本方法,列一元一次方程解应用题,同时也为后面的三个探究题打好基础。
【学情分析】学生在进入本节课的学习之前,需要掌握一元一次方程的解法及列方程解应用题的基本步骤。
【教学目标】
1.核心目标:了解用一元一次方程解工程问题的规律,理解把全部工作量看作1,掌握列方程解工程问题的方法。
2.过程与方法:体验将实际问题转化为数学问题的过程,进一步掌握列一元一次方程解实际问题的思想与方法。
3.情感态度价值观:探究“数学回归生活,服务于生活”题型,感受数学的实用价值,增强应用意识,激发学生学习数学的热情。
【教学重点】找出工程问题中的相等关系,建立方程模型,正确列出一元一次方程并进行求解;掌握解决实际问题的一般方法和步骤。?
【教学难点、关键】由实际问题抽象出数学模型的探究过程。
【教学方法】引导探究、讨论交流。
【教学手段】板书、多媒体、PPT。
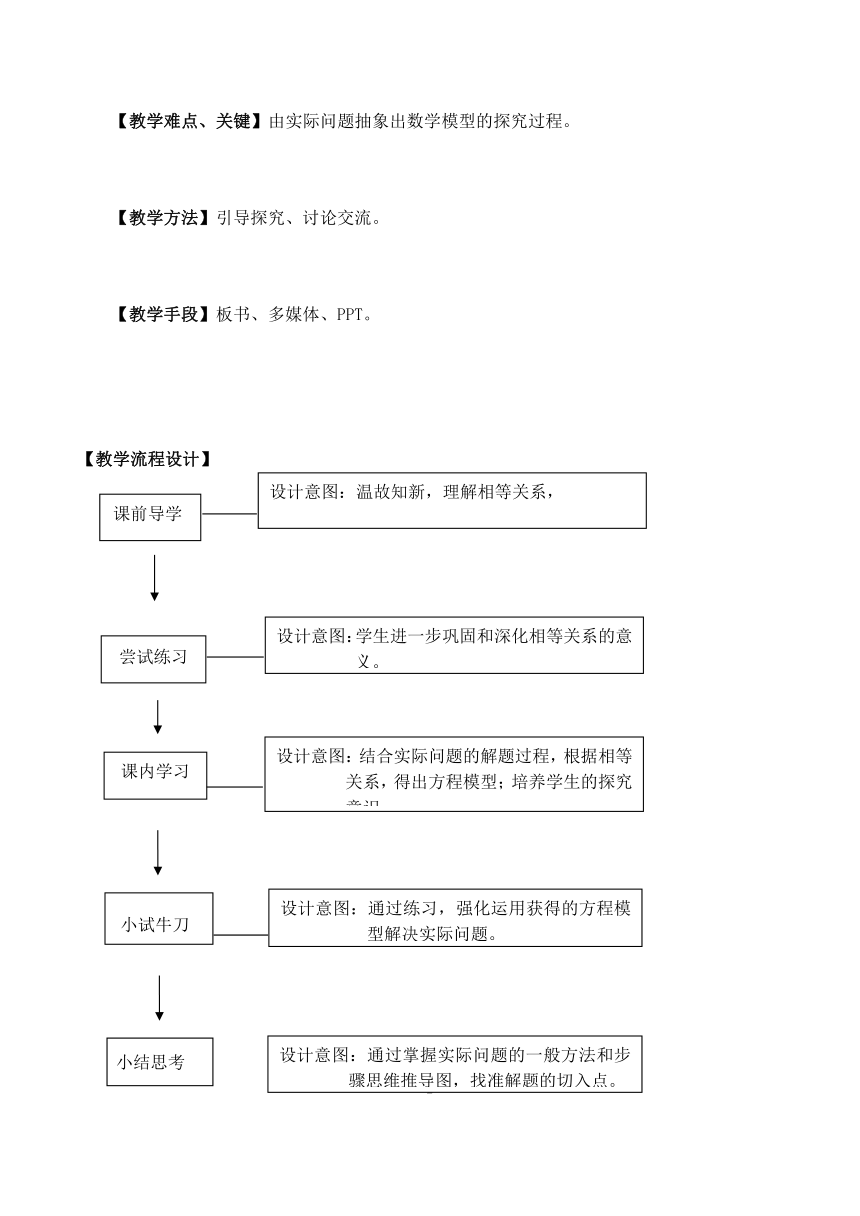
【教学流程设计】
【教学过程设计】
预习案
【课前导学】
问题1:列方程解应用问题的过程中,一般有哪些步骤?
答:(1)审题,分析题目中的相等关系;(2)设适当的未知数;(3)根据题目中的数量关系列方程;(4)解这个方程;(5)检验并答。
问题2:在工程问题中,我们通常见到工作总量、工作效率、工作时间这三个量,他们之间有什么关系?
答:工作总量
=工作效率×工作时间
师生活动:教师提问,学生思考、回答。
设计意图:通过提问,引导学生思考学习,温故知新,培养学生的表达能力,理解工程问题各个量之间的关系:工作总量=工作效率×工作时间。
【尝试练习】(对问题的初步认识)
问题3:一项工作,甲单独做10天完成,乙单独做15天完成,那么甲的工作效率是(
),乙的工作效率是(
);如果两人合作
天,那么甲完成工程的(
),乙完成工程的(
),两人共完成了这项工程的(
)。?
师生活动:教师指出,这类问题中,为了简单的表示数量关系,我们常常把总工作量看作
1。
设计意图:通过练习,学生进一步巩固和深化相等关系的意义,掌握解决问题的方法和过程,从而提高分析、解决问题的能力,体会到数学与生活的联系。
学习案
【知识点拨】
1.找出相应的工作总量、工作效率、工作时间。
2.找出相等关系并列方程。
【课内训练1】
例题讲解:整理一批图书,由一个人做要40
h
完成。现计划由一部分人先做4
h,然后增加
2人与他们一起做8
h
,完成这项工作。
假设这些人的工作效率相同,具体应该先安排多少人工作?
分析:讨论交流找到题目中的信息,教师引导回答。
这个题目与之前的题目区别在于哪些不同?
这项工作,分成几部分来完成?
工作量1
+
工作量2
=
工作总量
效率1×时间1
+
效率2×时间2
=
工作总量
人均效率×人数1
×时间1
+
人均效率×人数2
×时间2
=工作总量
(2)按要求填表,抓住等量关系:人均效率×人数×时间=工作总量
人均效率
人数
时间
工作量
前一部分工作
4
后一部分工作
8
(3)解:设安排
x
人先做4
h,依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2
答:应先安排
2人做4
小时。
师生活动:教师提出问题,学生思考、小组讨论回答。
设计意图:通过“推导图”分析,根据工程问题的数量关系,对加入人数以后的工程问题做出初步的梳理和加工,得出计算工作量的基本公式是:工作量=人均效率×人数×时间。再由学生完成填表,找到题目中已知量和未知量,然后通过合作交流,建立方程模型。?
【课内训练2】(课堂练习巩固)抓住等量关系
:工作效率×工作时间=工作总量
思考5:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.
如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设
x多少天可以铺好这条管线,
依题意得:
解方程,得:
=8
答:两队同时施工,要8天可以铺好这条管线。
【归纳】
用一元一次方程解决实际问题的基本过程:
设未知数,列方程
工程问题:
工作总量=工作效率
×
工作时间
=人均效率×人数×时间
各阶段工作量的和=总工作量
(总工作量未知,看作“1”)
设计意图:通过“导学图”,形象表示一元一次方程解决实际问题的基本过程,转化为“导航思维图”。找准做题的切入点。
反馈案
【利用一元一次方程解决工程问题
】
1.课堂小测(基础训练):
(1)整理一批数据,由一人做需
80
h
完成。现在计划先由一些人做
2
h
,再增加
5
人做
8
h
,完成这项工作的
。怎样安排参与整理数据的具体人数?
2.课后探讨(拓展提高):
(1)一个水池设有注水管和排水管,单独开注水管2小时注满水池,单独开排水管3小时可将一池水排完。现将注水管与排水管同时开放若干小时后,关上注水管,排水管排掉水池之水所用时间比两管同时开放的时间少
10
分钟,问两管同时开了多少时间?
(温馨提示,设两个管同时开放的时间
t
小时,
则排水管的工作时间为
(t-10/60
)小时)
设计意图:通过例题的学习,学会分析题意,总工作量=各部分工作量之和。找到等量关系的切入点,并能列方程求解。小测题把“完成这件工作”改为“完成这件工作的四分之三”。需认真读题,找到关键点。拓展是题一个知识的提升,特定情况下,各部分工作量是互相抵消的。让学生利用所学知识感受数学的灵活性与趣味性。进一步熟悉解决解决问题的方法和过程,从而提高分析和解决问题的能力。
【布置作业】?
1.完成拓展(2),并把方程求解并解答。
2.完成教材P106??习题3.4
第4题?
【板书设计】
板书
1.列方程解应用问题的一般步骤:
审、设、列、解、检答
2.相等关系:
工作总量=工作效率×工作时间
3.例题:
4.练习:
5.归纳:
3
-----工程问题
【教材】人教版数学
七年级
第三章
实际问题与一元一次方程。
【课时安排】第2课时。
【教学对象】七年级学生。
【教材分析】本节内容是学生在学习了代数式、简易方程及一元一次方程解法的基础上。对前一部分知识的应用与巩固,结合列方程解应用题的基本方法,列一元一次方程解应用题,同时也为后面的三个探究题打好基础。
【学情分析】学生在进入本节课的学习之前,需要掌握一元一次方程的解法及列方程解应用题的基本步骤。
【教学目标】
1.核心目标:了解用一元一次方程解工程问题的规律,理解把全部工作量看作1,掌握列方程解工程问题的方法。
2.过程与方法:体验将实际问题转化为数学问题的过程,进一步掌握列一元一次方程解实际问题的思想与方法。
3.情感态度价值观:探究“数学回归生活,服务于生活”题型,感受数学的实用价值,增强应用意识,激发学生学习数学的热情。
【教学重点】找出工程问题中的相等关系,建立方程模型,正确列出一元一次方程并进行求解;掌握解决实际问题的一般方法和步骤。?
【教学难点、关键】由实际问题抽象出数学模型的探究过程。
【教学方法】引导探究、讨论交流。
【教学手段】板书、多媒体、PPT。
【教学流程设计】
【教学过程设计】
预习案
【课前导学】
问题1:列方程解应用问题的过程中,一般有哪些步骤?
答:(1)审题,分析题目中的相等关系;(2)设适当的未知数;(3)根据题目中的数量关系列方程;(4)解这个方程;(5)检验并答。
问题2:在工程问题中,我们通常见到工作总量、工作效率、工作时间这三个量,他们之间有什么关系?
答:工作总量
=工作效率×工作时间
师生活动:教师提问,学生思考、回答。
设计意图:通过提问,引导学生思考学习,温故知新,培养学生的表达能力,理解工程问题各个量之间的关系:工作总量=工作效率×工作时间。
【尝试练习】(对问题的初步认识)
问题3:一项工作,甲单独做10天完成,乙单独做15天完成,那么甲的工作效率是(
),乙的工作效率是(
);如果两人合作
天,那么甲完成工程的(
),乙完成工程的(
),两人共完成了这项工程的(
)。?
师生活动:教师指出,这类问题中,为了简单的表示数量关系,我们常常把总工作量看作
1。
设计意图:通过练习,学生进一步巩固和深化相等关系的意义,掌握解决问题的方法和过程,从而提高分析、解决问题的能力,体会到数学与生活的联系。
学习案
【知识点拨】
1.找出相应的工作总量、工作效率、工作时间。
2.找出相等关系并列方程。
【课内训练1】
例题讲解:整理一批图书,由一个人做要40
h
完成。现计划由一部分人先做4
h,然后增加
2人与他们一起做8
h
,完成这项工作。
假设这些人的工作效率相同,具体应该先安排多少人工作?
分析:讨论交流找到题目中的信息,教师引导回答。
这个题目与之前的题目区别在于哪些不同?
这项工作,分成几部分来完成?
工作量1
+
工作量2
=
工作总量
效率1×时间1
+
效率2×时间2
=
工作总量
人均效率×人数1
×时间1
+
人均效率×人数2
×时间2
=工作总量
(2)按要求填表,抓住等量关系:人均效率×人数×时间=工作总量
人均效率
人数
时间
工作量
前一部分工作
4
后一部分工作
8
(3)解:设安排
x
人先做4
h,依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2
答:应先安排
2人做4
小时。
师生活动:教师提出问题,学生思考、小组讨论回答。
设计意图:通过“推导图”分析,根据工程问题的数量关系,对加入人数以后的工程问题做出初步的梳理和加工,得出计算工作量的基本公式是:工作量=人均效率×人数×时间。再由学生完成填表,找到题目中已知量和未知量,然后通过合作交流,建立方程模型。?
【课内训练2】(课堂练习巩固)抓住等量关系
:工作效率×工作时间=工作总量
思考5:一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.
如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
解:设
x多少天可以铺好这条管线,
依题意得:
解方程,得:
=8
答:两队同时施工,要8天可以铺好这条管线。
【归纳】
用一元一次方程解决实际问题的基本过程:
设未知数,列方程
工程问题:
工作总量=工作效率
×
工作时间
=人均效率×人数×时间
各阶段工作量的和=总工作量
(总工作量未知,看作“1”)
设计意图:通过“导学图”,形象表示一元一次方程解决实际问题的基本过程,转化为“导航思维图”。找准做题的切入点。
反馈案
【利用一元一次方程解决工程问题
】
1.课堂小测(基础训练):
(1)整理一批数据,由一人做需
80
h
完成。现在计划先由一些人做
2
h
,再增加
5
人做
8
h
,完成这项工作的
。怎样安排参与整理数据的具体人数?
2.课后探讨(拓展提高):
(1)一个水池设有注水管和排水管,单独开注水管2小时注满水池,单独开排水管3小时可将一池水排完。现将注水管与排水管同时开放若干小时后,关上注水管,排水管排掉水池之水所用时间比两管同时开放的时间少
10
分钟,问两管同时开了多少时间?
(温馨提示,设两个管同时开放的时间
t
小时,
则排水管的工作时间为
(t-10/60
)小时)
设计意图:通过例题的学习,学会分析题意,总工作量=各部分工作量之和。找到等量关系的切入点,并能列方程求解。小测题把“完成这件工作”改为“完成这件工作的四分之三”。需认真读题,找到关键点。拓展是题一个知识的提升,特定情况下,各部分工作量是互相抵消的。让学生利用所学知识感受数学的灵活性与趣味性。进一步熟悉解决解决问题的方法和过程,从而提高分析和解决问题的能力。
【布置作业】?
1.完成拓展(2),并把方程求解并解答。
2.完成教材P106??习题3.4
第4题?
【板书设计】
板书
1.列方程解应用问题的一般步骤:
审、设、列、解、检答
2.相等关系:
工作总量=工作效率×工作时间
3.例题:
4.练习:
5.归纳:
3
