人教版九年级数学下册第29章 投影与视图 全章教案
文档属性
| 名称 | 人教版九年级数学下册第29章 投影与视图 全章教案 |

|
|
| 格式 | DOCX | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 18:43:27 | ||
图片预览




文档简介
第29章
投影与视图
第一课时 平行投影与中心投影
1.了解投影的有关概念,能根据投影线的方向辨认物体的投影.
2.了解中心投影和平行投影的概念,并理解中心投影和平行投影的区别.
3.学会关注生活中有关投影的数学问题,提高数学应用意识.
正确区分投影中光源、投影面、投影线等概念.
在投影面上画出平面图形的平行投影或中心投影.
一、情景导入
影子舞,通常是由艺术家透过光影,用肢体语言表达情感,使现场效果宛如黑白电影,时尚而又返古的一种适合小型舞台表演的舞蹈(如下图).影子舞就是充分将灯光、物体、屏幕、音乐等巧妙结合的艺术表现形式.这节课我们就来研究灯光与影子的问题.
问题:影子的形成需要几个要素?影子是怎样形成的?
二、自学互研
阅读教材P87-88,完成下列问题:
问题1:什么是投影?
出示投影,让学生感受在日常生活中的一些投影现象.
结论:一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面.
问题2:观察探照灯光的一束光中的光线与灯泡发出的光线有什么不同?分别用这两种光线得到的投影有何不同?
结论:有时光线是一组互相平行的射线,例如太阳光或探照灯光的一束光中的光线.由平行光线形成的投影叫做平行投影.例如,物体在太阳光的照射下形成的影子(简称日影)就是平行投影.
平行投影与中心投影的区别与联系:
区别
光线
物体与投
影面平行
时的投影
联系
平行
投影
平行的
投射线
全等
中心
投影
从一点出发
的投射线
放大(位
似变换)
都是物体在光线的照射
下,在某个平面内形成
的影子(即都是投影)
师生活动:
①明了学情:关注学生对平行投影、中心投影的理解与掌握.
②差异指导:深入到各小组指导操作,及时提醒和点拨.
③生生互助:小组内合作交流,对产生不同意见的地方相互解疑释难.
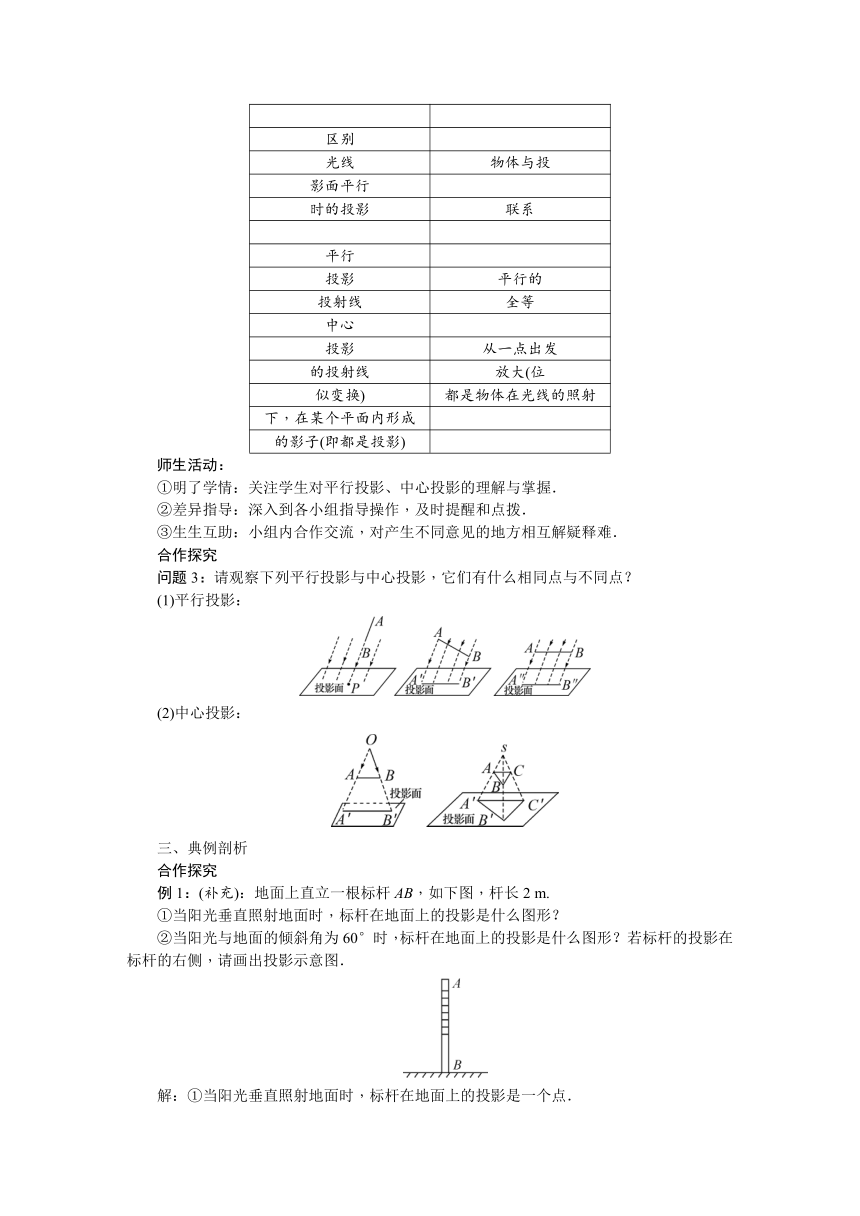
问题3:请观察下列平行投影与中心投影,它们有什么相同点与不同点?
(1)平行投影:
(2)中心投影:
三、典例剖析
例1:(补充):地面上直立一根标杆AB,如下图,杆长2 m.
①当阳光垂直照射地面时,标杆在地面上的投影是什么图形?
②当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?若标杆的投影在标杆的右侧,请画出投影示意图.
解:①当阳光垂直照射地面时,标杆在地面上的投影是一个点.
②当阳光与地面的倾斜角为60°时,标杆在地面上的投影是一条线段,投影如下图所示:
例2:如图,△DEF是△ABC在光源O下的投影,当△ABC自下向上运动时,其投影△DEF如何变化?当点B在OE何处时,△ABC的面积是其投影△DEF面积的四分之一?
(学生合作完成)
四、课堂小结
(1)本节课主要学习了哪些知识?学习了哪些数学思想和方法?
(2)本节课还有哪些疑惑?说一说!
师生总结:主要内容有投影、投影面、投影线、平行投影和中心投影的概念.
主要技能是在投影面上画出物体的中心投影,并能通过投影分析出点光源的具体位置.
五、检测反馈
1.下列影子属于中心投影的是( C )
A.阳光下旗杆的影子 B.阳光下小树的影子
C.灯光下的手影 D.阳光下张玲的影子
2.某一时刻,身高1.6 m的小明在阳光下的影长是0.4 m,在同一时刻同一地点,测得一根旗杆的影长是5 m,则该旗杆的高度为( C )
A.1.25 m B.10 m
C.20 m D.8 m
3.一般而言,对同一建筑物,相同时刻在阳光下的影子,冬天比夏天( B )
A.短 B.长
C.看具体时间 D.无法比较
4.如图,不透明圆锥体DEC放在水平面上,在A处灯光照射下形成影子,设BP过底面圆的圆心,已知圆锥体高2 m,底面半径为2 m,BE=4 m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距水平面的高度.
解:(1)如图,圆锥的高DO=2,在Rt△DOB中,OB=BE+EO=4+2=6,∴tan∠B===,∴∠B=30°;
(2)过点A作AF⊥BP,垂足为点F.∵∠B=30°,∴∠ACP=2∠B=60°.又∠ACP=∠B+∠BAC,∴∠B=∠BAC,∴AC=BC=BE+EC=8.在Rt△ACF中,AF=AC·sin∠ACF=8sin60°=4.
六、课后作业
第二课时 正投影
1.了解正投影的概念,能根据正投影的性质画出简单平面图形的正投影.
2.在经历观察、探究、思考、归纳的过程中,掌握正投影的特征.
3.培养抽象、概括能力,发展空间想象.
正投影的含义及其性质.
归纳正投影的性质,正确画出简单平面图的正投影.
一、情景导入
下图表示一块三角尺在光线照射下形成投影,其中哪个是平行投影?哪个是中心投影?图(2)、图(3)的投影线与投影面的位置关系有什么区别?
像图(3)这样,投影线垂直于投影面产生的投影叫做正投影.
二、自学互研
阅读教材P88-91内容,完成下列问题:
问题1:把一根直的细铁丝(记为线段AB)放在三个不同的位置:
三种情形下铁丝的正投影各是什么图形?大小有何关系?
结论:①正投影是线段,线段长等于正投影长;
②正投影是线段,线段长大于正投影长;
③正投影是一个点.
问题2:把一块正方形硬纸板(记为正方形ABCD)放在三个不同的位置:
(1)纸板平行于投影面;(2)纸板倾斜于投影面;(3)纸板垂直于投影面.
三种情形下纸板的正投影各是什么图形?大小有何关系?
结论:①纸板的正投影与纸板的形状、大小一样;
②纸板的正投影与纸板的形状、大小不完全一样;
③纸板的正投影为一条线段.
问题3:当物体的某个面平行于投影面时,这个面的正投影与这个面有怎样的关系?
答:正投影性质:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
师生活动:
①明了学情:关注学生对正投影性质的探究过程,了解学生对其理解与掌握情况.
②差异指导:深入小组,对学生产生的疑惑适时点拨.
③生生互助:小组内交流、合作、相互释疑解难.
三、典例剖析
例:画出如图摆放的正方体在投影面P上的正投影.
(1)正方体的一个面ABCD平行于投影面P;
(2)正方体的一个面ABCD倾斜于投影面P,上底面ADEF垂直于投影面P,并且上底面的对角线AE垂直于投影面P.
解:(1)如下图(1),正方体的正投影为正方形A′B′C′D′,它与正方体的一个面是全等关系.
(2)如下图(2),正方体的正投影为矩形F′G′C′D′,这个矩形的长等于正方体的底面对角线长,矩形的宽等于正方体的棱长.矩形上、下两边中点连线A′B′是正方体的侧棱AB及它所对的另一条侧棱EH的投影.
师生活动:
学生独立思考,解决例题,然后与同伴交流,教师巡视,对有困难的学生,适当引导解决.让两名学生展示,师生共同点评.
四、课堂小结
(1)本节课主要学习了哪些知识?重点研究了什么问题?
(2)对于本节课的知识,你还有哪些疑惑?请说给老师和同学们听听:
五、检测反馈
1.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能是( A )
,A) ,B) ,C) ,D)
2.若线段AB在投影面上的正投影为A1B1,则线段AB与线段A1B1的大小关系是( D )
A.AB=A1B1 B.AB>A1B1
C.AB<A1B1 D.AB≥A1B1
3.如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论:①BC2=BD·AB;②CD2=AD·BD.
解:(1)AC的投影是AD,CD的投影是点D,CB的投影是BD;
(2)①∵CD⊥AB,∴∠CDB=∠ACB=90°.又∵∠B=∠B,∴△BCD∽△BAC,∴=,∴BC2=BD·AB;
②∵∠ACB=90°,∴∠ACD+∠BCD=90°.∵CD⊥AB,∴∠ACD+∠BAC=90°.∴∠BCD=∠BAC.又∵∠ADC=∠BDC=90°,∴△ACD∽△CBD,∴=,∴CD2=AD·BD.
六、课后作业
第三课时 三视图
1.会从投影的角度理解视图的概念.
2.会画简单几何体的三视图.
3.通过观察探究等活动,知道物体的三视图与正投影的相互关系及三视图中的位置关系、大小关系.
从投影的角度加深对三视图的理解,会画简单物体的三视图.
正确观察物体,按规则画出三视图.
一、情景导入
多媒体播放古诗《题西林壁》的配画朗诵视频.
【宋】苏轼
横看成岭侧成峰,远近高低各不同.
不识庐山真面目,只缘身在此山中.
古诗《题西林壁》一句“横看成岭侧成峰,远近高低各不同”中蕴含着怎样的数学道理?
二、自学互研
阅读教材P94-97内容,完成下列问题:
问题1:张师傅是铸造厂的工人,想让他制作一个如图所示的小零件.
(1)如何准确地表达小零件的尺寸大小?
(2)除了用文字语言,可不可以用图形语言表示?
(3)你们在生活中见过三视图吗?
问题2:对长方体的六个面进行正投影,并思考为什么选择用三视图来表达几何体的形状及尺寸.
(1)选择什么样的视图可以比较准确全面的表达几何体?
(2)我们从六个不同方向对长方体进行正投影,可以分别得到什么样的视图?
(3)这些视图分别反映了几何体的哪些尺寸?
(4)只要观察哪些视图就可以比较全面的表达这个长方体的形状、大小?
归纳:在正面内得到的由前向后观察物体的视图,叫做主视图.
在水平面内得到的由上向下观察物体的视图,叫做俯视图.
在侧面内得到的由左向右观察物体的视图,叫做左视图.
探究三视图的画法
(1)课件展示:如图①,对几何体进行正投影得到三视图.
(2)将水平面、侧面、正面展开到同一平面,观察得到的三种视图的位置关系.
(3)同桌讨论得到的三种视图在大小上的规律,如图②.
归纳:三个视图的大小是互相联系的,画三视图时,三个视图要放在正确的位置.并且使主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
画图时规定:看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
师生活动:
①明了学情:关注学生是否理解用投影定义视图,是否理解用三种视图表示立体图形的意义.
②差异指导:对学生在探究过程中产生的疑惑适时点拨.
③生生互助:小组内交流、讨论,形成共识.
三、典例剖析
例1:画出下图所示的一些基本几何体的三视图.
分析:画这些基本几何体的三视图时,要注意从三个方向观察它们.具体画法为:
(1)确定主视图的位置,画出主视图;
(2)在主视图正下方画出俯视图,注意与主视图“长对正”.
(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
解:
例2:画出如图(1)所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
分析:支架的形状是由两个大小不等的长方体构成的组合体.画三视图时要注意这两个长方体的上下、前后位置关系.
解:如上图(2)所示,是支架的三视图.
师生活动:
学生独立思考、观察、解决例题,并与同伴交流,教师巡视,适当引导学生解决.
四、课堂小结
(1)本节课主要学习了哪些知识?重点研究了什么问题?
(2)通过这些内容的学习,你知道画一个物体的三视图的步骤吗?
教师强调:确定好三视图的位置,“长对正”“高平齐”“宽相等”.
五、检测反馈
1.下列几何体的主视图不是中心对称图形的是( B )
,A) ,B) ,C) ,D)
2.下面的几何体中,主视图为三角形的是( C )
,A) ,B) ,C) ,D)
3.在①长方体,②正方体,③圆锥,④圆柱,⑤三棱柱,⑥球,这六种几何体中,其主视图、左视图、俯视图都完全相同的是__②⑥__(填上序号即可).
六、课后作业
第四课时 由三视图描述几何体
1.会根据物体的三视图描述出几何体形状或实物原型.
2.经历探索简单几何体三视图来描述几何体的形状的过程,进一步发展空间想象能力.
根据物体的三视图想象出几何体的形状或实物原型.
由物体的三视图得到它的平面展开图的转化.
一、情景导入
问题1:请你找出图中所示物体所对应的主视图.
问题2:若一个物体的三视图都是圆,则这个物体是什么呢?
二、自学互研
阅读教材P98例3,完成下列问题:
1.由三视图想象立体图形时,要分别根据主视图、俯视图、左视图想象立体图形__正__面、__上__面、__左__面,然后再结合起来考虑整体图形.
2.一个立体图形的俯视图是圆,则这个图形可能是__圆锥、圆柱__.
3.其主视图、左视图与俯视图均相同的是__正方体和球__.
1.一个立体图形的三视图是一个正方形和两个长方形,则这个图形是( B )
A.正方体 B.长方体 C.四面体 D.四棱锥
2.如图,三视图所表示的物体是__五棱锥__.
3.根据下列物体的三视图,判断该几何体是__圆台__.
方法归纳:先看主视图和俯视图(或左视图),再综合左视图(或俯视图),根据几何体从三个角度观察得到的图形,综合得出几何体原形.
师生活动:
①明了学情:关注学生是否体会到由实物到视图的想象是“分”的过程,由视图到实物的想象是“合”的过程.
②差异指导:深入小组,对学生在探究中产生的疑惑及时引导与点拨.
③生生互助:学生小组内交流、讨论、相互解疑释难.
三、典例剖析
例1:根据下面的三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
解:(1)从三个方向看立体图形,视图都是矩形,可以想象这个立体图形是长方体,如下图(1)所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形;从上面看,视图是圆;可以想象这个立体图形是圆锥,如下图(2)所示.
例2:根据物体的三视图(如下图),描述物体的形状.
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到,另有两条棱(虚线表示)被遮挡;由左视图可知,物体左侧有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
解:物体是正五棱柱形状的,如下图所示:
师生活动:
学生独立观察,思考解决例题,然后小组内交流讨论,并积极主动到黑板展示,教师在巡视中对学生及时进行点拨.
四、课堂小结
(1)三视图的作用是什么?
(2)由三视图怎样想象出立体图形?
教师总结:(1)三视图可以表示立体图形;(2)根据主视图、俯视图和左视图分别想象立体图形的正面、上面和左面的形状,再综合起来想象它的整体形状.
五、检测反馈
1.一个几何体的三个视图如图所示,这个几何体是( A )
A.圆柱 B.球 C.圆锥 D.正方体
2.一张桌子摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上碟子共有( C )
A.9个 B.10个 C.12个 D.13个
3.如图①是一块带有圆形空洞和方形空洞的小木板,则图②所示的几何体中既可以堵住圆形空洞,又可以堵住方形空洞的是( B )
4.“横看成岭侧成峰,远近高低各不同”是从正面、侧面、高处往低处俯视,这三种角度看风景.如果一个实物正面看是三角形,侧面看也是三角形,上面看是带圆心的圆,那么这个实物是__圆锥__.
六、课后作业
第五课时 由三视图到展开图
1.能根据三视图想象出基本几何体的展开图.
2.在探究由三视图想象出立体图形的过程中,初步建立空间观念,发展几何直觉和形象思维 ,培养空间想象能力.
根据三视图描述基本几何体和实物原型及计算几何体的表面积等.
根据三视图想象出立体图形的表面展开图,计算立体图形的表面积、体积等.
一、情景导入
某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如图),请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm)
二、自学互研
阅读教材P99内容,解答例5提出的问题:
问题分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际生产中,三视图和展开图往往结合在一起使用.解决活动一中的问题的思路是先由三视图想象出密封罐的形状,再进一步画出展开图,然后计算面积.
解:由三视图可知,密封罐的形状是正六棱柱(如图①).
密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,图②是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为:
6×50×50+2×6××50×50sin60°
=6×502×
≈27990(mm2)
教师可给学生提供一个思路:解决本题的思路是先由视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
师生活动:
①明了学情:关注学生能否由三视图想象实物体,再画出实物展开图.
②差异指导:深入小组内对学生的疑惑及时引导、点拨.
③生生互助:小组内合作交流、相互解疑释难、达成共识.
三、典例剖析
例1:某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个茶叶罐所需钢板的面积.
解:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面直径为100,高为150.
因为每个密封罐所需钢板的面积即为该圆柱体的表面积,所以S=2π×502+2π×50×150=20000π.
例2:如图是由一些棱长为1 cm的正方体小木块搭建成的几何体的主视图、俯视图和左视图,请问:
(1)这个几何体是由多少个小木块组成的?
(2)在俯视图中标出相应位置小木块的个数;
(3)求出该几何体的表面积(包括底面).
分析:(1)由俯视图可得该组合几何体最底层的木块个数,由主视图或左视图可得第二层和第三层的小木块的个数,相加即可;
(2)根据上题得到的小木块的个数,在俯视图上标出来即可;
(3)将几何体的各个面的面积相加即可得到其表面积.
师生活动:
教师展示图片,由学生先独立思考、想象,再小组内探究体验,合作、交流、展示.
四、课堂小结
(1)本节课主要学习了哪些知识?
(2)对于本课时所学习的知识还存在哪些疑惑?
教师强调:三视图与平面展开图的相互转化:三视图——实物——平面展开图.
五、检测反馈
1.(杭州中考)已知某几何体的三视图(单位:cm)如图所示,则该几何体的侧面积等于( B )
A.12π cm2 B.15π cm2
C.24π cm2 D.30π cm2
,(第1题图)) ,(第2题图))
2.一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的表面积为( D )
A.2π B.6π
C.7π D.8π
3.如图是一个几何体的三视图,其中俯视图为正三角形,则这个几何体的侧面积是( A )
A.18 cm2 B.20 cm2
C.(18+2)cm2 D.(18+4)cm2
,(第3题图)) ,(第4题图))
4.如图是一个上下底密封纸盒的三视图,根据图中数据,可计算这个密封纸盒的表面积为__(75+360)__cm2(结果可保留根号).
六、课后作业
第六课时 制作立体模型
1.在实际动手活动中进一步加深对投影和视图知识的认识,加强在实践活动中手脑结合的能力.
2.通过制作模型,体会由平面图形转化为立体图形的过程与乐趣.
3.通过动手实践活动,培养学生的创新意识与发明创造意识.
让学生亲自经历规律的发现、深入、研究、应用的过程.
学生通过手工制作,实现理论与实践的结合.
一、情景导入
下列模型是如何得到的?
以上立体图形都是通过拼接平面图形得到的,如何制作平面图形,从而拼接得到立体图形呢?
二、自学互研
阅读“课题学习”,完成下列问题:
问题1:以硬纸板为主要材料,分别做出下面的两组三视图表示的立体模型.
问题2:按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型.
展示作品:教师展示学生的优秀作品,学生共同鉴赏评品.
师生活动:
教师提问,想一想上面两组三视图,分别表示什么实物模型?学生确定了实物模型的形状后,利用马铃薯动手制作,在制作过程中,教师强调安全、有序,确保活动顺利进行,学生制作完成后,教师展示课前制作好的模型样品,供学生参考、比较.
三、典例剖析
例:下面的每一组平面图形都是由四个等边三角形组成的.
(1)指出其中哪些可以折叠成多面体,并把上面的图形描在纸上,剪下来,叠一叠,验证你的答案;
(2)画出由上面图形能折叠成的多面体的三视图,并指出三视图中是怎样体现“长对正、高平齐、宽相等”的;
(3)如果上图中小三角形的边长为1,那么对应的多面体的体积和表面积各是多少?
解:(1)经过验证,图①②③都可以折成多面体.
(2)先确定能折叠成的多面体为三棱锥,其三视图如图所示.
(3)如果图中的小三角形的边长为1,那么对应的多面体的体积都是Sh=××1×1=,表面积都是×1×1×4=.
活动结论:
1.数学是以数量关系和空间形式为主要研究对象的学科,数量关系和空间形式是从现实世界中抽象出来的.投影和视图的知识是从实际需要(建筑、制造等)中产生的,它们与实际生活联系得非常紧密.
2.从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得出立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力是非常重要的.
四、课堂小结
通过本节课的学习,你有了哪些新的收获或疑问?
说出你的想法与同学们分享.
五、检测反馈
1.如图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是__①②④__(把正确的立体图形的序号都填在横线上).
2.如图中的图形是由一个扇形和一个圆组成的.
(1)把图中的图形描在纸上,剪下来,围成一个圆锥;
(2)画出图中的图形围成的圆锥的三视图;
(3)如果图中的扇形的半径为13,圆的半径为5,那么围成的圆锥的体积是多少?
解:(1)在纸片上用铅笔描出上面的图形,围成一个圆锥,如图所示.
(2)画出围成的圆锥的左视图、主视图、俯视图如图所示.
(3)如图所示,扇形的半径为13,圆的半径为5,在直角三角形中,圆锥的高度为=12,圆锥的体积V=Sh=×π×52×12=100π.
六、课后作业
第二十九章总结与提升
1.进一步理解投影、三视图等概念.
2.能画出几何体的三视图,能根据三视图想象物体的形状.
进一步加深对本章知识的理解,提高解题技能.
利用三视图想象实物形状,并根据相关数据进行计算.
一、情景导入
本章知识结构图:
二、自学互研
通阅本章内容,完成下列问题:
问题1:平行投影和中心投影的区别是什么?如何判别物体的投影是平行投影还是中心投影?
答:区别在于平行投影是在平行光线下形成的投影,而中心投影是在相交光线下形成的投影.区别这两种投影的关键是抓住光线的特征.
问题2:如图,晚上小明在路灯下散步,在小明由A处走到B处这一过程中,他在地上的影子( C )
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
问题3:下图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的左视图是( A )
,A) ,B) ,C) ,D)
问题4:如图是某种物体的三视图及相关数据(单位:cm),求该物体的体积(≈1.732,π=3.14,精确到0.01 cm3).
解:S底=6××0.8×=(cm2),V=×1-π(0.4)2×1=-≈≈1.16032≈1.16(cm3).
师生活动:
①明了学情:关注学生对本章知识的掌握与运用情况.
②差异指导:对探究中学生遗忘的知识及时引导与点拨.
③生生互助:小组合作、交流讨论、达成共识.
三、典例剖析
例1:如图是一个几何体的三视图,这个几何体的表面积为________(π取3.14).
解析:这个几何体是圆锥.圆锥的底面半径为1,母线长为2,所以圆锥的侧面积是×2π×2=2π,底面积是π,则表面积是2π+π=3π≈9.42.
答案:9.42
例2:用小正方体木块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗?它最少需要多少个小正方体木块?最多需要多少个小正方体木块?
解:这样的几何体不唯一,它最少需要10个小正方体木块,最多需要16个小正方体木块,其中,第一层7块,第二层至少2块,最多6块,第三层至少1块,最多3块.
俯视图中小方格内的数字表示所放的小正方体的最少如图(1),最多如图(2).
师生活动:
学生观察、思考、相互交流,进一步加强对本章重要知识点的理解与运用,老师巡视,适时对学生进行引导分析.
四、课堂小结
通过本节课学习,你对本章知识又有了哪些新的认识?还有什么疑惑?请说给老师和同学们听听?
五、检测反馈
1.如图放置的几何体的左视图是( C )
,A) ,B) ,C) ),\s\do5(D))
2.由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是( A )
A.3 B.4 C.5 D.6
3.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是__72__.
4.如图是某几何体的展开图.
(1)这个几何体的名称是;
(2)画出这个几何体的三视图;
(3)求出这个几何体的体积.(π取3.14)
解:(1)圆柱;
(2)三视图为:;
(3)体积为V=πr2h=3.14×52×20=1570.
六、课后作业
投影与视图
第一课时 平行投影与中心投影
1.了解投影的有关概念,能根据投影线的方向辨认物体的投影.
2.了解中心投影和平行投影的概念,并理解中心投影和平行投影的区别.
3.学会关注生活中有关投影的数学问题,提高数学应用意识.
正确区分投影中光源、投影面、投影线等概念.
在投影面上画出平面图形的平行投影或中心投影.
一、情景导入
影子舞,通常是由艺术家透过光影,用肢体语言表达情感,使现场效果宛如黑白电影,时尚而又返古的一种适合小型舞台表演的舞蹈(如下图).影子舞就是充分将灯光、物体、屏幕、音乐等巧妙结合的艺术表现形式.这节课我们就来研究灯光与影子的问题.
问题:影子的形成需要几个要素?影子是怎样形成的?
二、自学互研
阅读教材P87-88,完成下列问题:
问题1:什么是投影?
出示投影,让学生感受在日常生活中的一些投影现象.
结论:一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影.照射光线叫做投影线,投影所在的平面叫做投影面.
问题2:观察探照灯光的一束光中的光线与灯泡发出的光线有什么不同?分别用这两种光线得到的投影有何不同?
结论:有时光线是一组互相平行的射线,例如太阳光或探照灯光的一束光中的光线.由平行光线形成的投影叫做平行投影.例如,物体在太阳光的照射下形成的影子(简称日影)就是平行投影.
平行投影与中心投影的区别与联系:
区别
光线
物体与投
影面平行
时的投影
联系
平行
投影
平行的
投射线
全等
中心
投影
从一点出发
的投射线
放大(位
似变换)
都是物体在光线的照射
下,在某个平面内形成
的影子(即都是投影)
师生活动:
①明了学情:关注学生对平行投影、中心投影的理解与掌握.
②差异指导:深入到各小组指导操作,及时提醒和点拨.
③生生互助:小组内合作交流,对产生不同意见的地方相互解疑释难.
问题3:请观察下列平行投影与中心投影,它们有什么相同点与不同点?
(1)平行投影:
(2)中心投影:
三、典例剖析
例1:(补充):地面上直立一根标杆AB,如下图,杆长2 m.
①当阳光垂直照射地面时,标杆在地面上的投影是什么图形?
②当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?若标杆的投影在标杆的右侧,请画出投影示意图.
解:①当阳光垂直照射地面时,标杆在地面上的投影是一个点.
②当阳光与地面的倾斜角为60°时,标杆在地面上的投影是一条线段,投影如下图所示:
例2:如图,△DEF是△ABC在光源O下的投影,当△ABC自下向上运动时,其投影△DEF如何变化?当点B在OE何处时,△ABC的面积是其投影△DEF面积的四分之一?
(学生合作完成)
四、课堂小结
(1)本节课主要学习了哪些知识?学习了哪些数学思想和方法?
(2)本节课还有哪些疑惑?说一说!
师生总结:主要内容有投影、投影面、投影线、平行投影和中心投影的概念.
主要技能是在投影面上画出物体的中心投影,并能通过投影分析出点光源的具体位置.
五、检测反馈
1.下列影子属于中心投影的是( C )
A.阳光下旗杆的影子 B.阳光下小树的影子
C.灯光下的手影 D.阳光下张玲的影子
2.某一时刻,身高1.6 m的小明在阳光下的影长是0.4 m,在同一时刻同一地点,测得一根旗杆的影长是5 m,则该旗杆的高度为( C )
A.1.25 m B.10 m
C.20 m D.8 m
3.一般而言,对同一建筑物,相同时刻在阳光下的影子,冬天比夏天( B )
A.短 B.长
C.看具体时间 D.无法比较
4.如图,不透明圆锥体DEC放在水平面上,在A处灯光照射下形成影子,设BP过底面圆的圆心,已知圆锥体高2 m,底面半径为2 m,BE=4 m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距水平面的高度.
解:(1)如图,圆锥的高DO=2,在Rt△DOB中,OB=BE+EO=4+2=6,∴tan∠B===,∴∠B=30°;
(2)过点A作AF⊥BP,垂足为点F.∵∠B=30°,∴∠ACP=2∠B=60°.又∠ACP=∠B+∠BAC,∴∠B=∠BAC,∴AC=BC=BE+EC=8.在Rt△ACF中,AF=AC·sin∠ACF=8sin60°=4.
六、课后作业
第二课时 正投影
1.了解正投影的概念,能根据正投影的性质画出简单平面图形的正投影.
2.在经历观察、探究、思考、归纳的过程中,掌握正投影的特征.
3.培养抽象、概括能力,发展空间想象.
正投影的含义及其性质.
归纳正投影的性质,正确画出简单平面图的正投影.
一、情景导入
下图表示一块三角尺在光线照射下形成投影,其中哪个是平行投影?哪个是中心投影?图(2)、图(3)的投影线与投影面的位置关系有什么区别?
像图(3)这样,投影线垂直于投影面产生的投影叫做正投影.
二、自学互研
阅读教材P88-91内容,完成下列问题:
问题1:把一根直的细铁丝(记为线段AB)放在三个不同的位置:
三种情形下铁丝的正投影各是什么图形?大小有何关系?
结论:①正投影是线段,线段长等于正投影长;
②正投影是线段,线段长大于正投影长;
③正投影是一个点.
问题2:把一块正方形硬纸板(记为正方形ABCD)放在三个不同的位置:
(1)纸板平行于投影面;(2)纸板倾斜于投影面;(3)纸板垂直于投影面.
三种情形下纸板的正投影各是什么图形?大小有何关系?
结论:①纸板的正投影与纸板的形状、大小一样;
②纸板的正投影与纸板的形状、大小不完全一样;
③纸板的正投影为一条线段.
问题3:当物体的某个面平行于投影面时,这个面的正投影与这个面有怎样的关系?
答:正投影性质:当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
师生活动:
①明了学情:关注学生对正投影性质的探究过程,了解学生对其理解与掌握情况.
②差异指导:深入小组,对学生产生的疑惑适时点拨.
③生生互助:小组内交流、合作、相互释疑解难.
三、典例剖析
例:画出如图摆放的正方体在投影面P上的正投影.
(1)正方体的一个面ABCD平行于投影面P;
(2)正方体的一个面ABCD倾斜于投影面P,上底面ADEF垂直于投影面P,并且上底面的对角线AE垂直于投影面P.
解:(1)如下图(1),正方体的正投影为正方形A′B′C′D′,它与正方体的一个面是全等关系.
(2)如下图(2),正方体的正投影为矩形F′G′C′D′,这个矩形的长等于正方体的底面对角线长,矩形的宽等于正方体的棱长.矩形上、下两边中点连线A′B′是正方体的侧棱AB及它所对的另一条侧棱EH的投影.
师生活动:
学生独立思考,解决例题,然后与同伴交流,教师巡视,对有困难的学生,适当引导解决.让两名学生展示,师生共同点评.
四、课堂小结
(1)本节课主要学习了哪些知识?重点研究了什么问题?
(2)对于本节课的知识,你还有哪些疑惑?请说给老师和同学们听听:
五、检测反馈
1.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影不可能是( A )
,A) ,B) ,C) ,D)
2.若线段AB在投影面上的正投影为A1B1,则线段AB与线段A1B1的大小关系是( D )
A.AB=A1B1 B.AB>A1B1
C.AB<A1B1 D.AB≥A1B1
3.如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论:①BC2=BD·AB;②CD2=AD·BD.
解:(1)AC的投影是AD,CD的投影是点D,CB的投影是BD;
(2)①∵CD⊥AB,∴∠CDB=∠ACB=90°.又∵∠B=∠B,∴△BCD∽△BAC,∴=,∴BC2=BD·AB;
②∵∠ACB=90°,∴∠ACD+∠BCD=90°.∵CD⊥AB,∴∠ACD+∠BAC=90°.∴∠BCD=∠BAC.又∵∠ADC=∠BDC=90°,∴△ACD∽△CBD,∴=,∴CD2=AD·BD.
六、课后作业
第三课时 三视图
1.会从投影的角度理解视图的概念.
2.会画简单几何体的三视图.
3.通过观察探究等活动,知道物体的三视图与正投影的相互关系及三视图中的位置关系、大小关系.
从投影的角度加深对三视图的理解,会画简单物体的三视图.
正确观察物体,按规则画出三视图.
一、情景导入
多媒体播放古诗《题西林壁》的配画朗诵视频.
【宋】苏轼
横看成岭侧成峰,远近高低各不同.
不识庐山真面目,只缘身在此山中.
古诗《题西林壁》一句“横看成岭侧成峰,远近高低各不同”中蕴含着怎样的数学道理?
二、自学互研
阅读教材P94-97内容,完成下列问题:
问题1:张师傅是铸造厂的工人,想让他制作一个如图所示的小零件.
(1)如何准确地表达小零件的尺寸大小?
(2)除了用文字语言,可不可以用图形语言表示?
(3)你们在生活中见过三视图吗?
问题2:对长方体的六个面进行正投影,并思考为什么选择用三视图来表达几何体的形状及尺寸.
(1)选择什么样的视图可以比较准确全面的表达几何体?
(2)我们从六个不同方向对长方体进行正投影,可以分别得到什么样的视图?
(3)这些视图分别反映了几何体的哪些尺寸?
(4)只要观察哪些视图就可以比较全面的表达这个长方体的形状、大小?
归纳:在正面内得到的由前向后观察物体的视图,叫做主视图.
在水平面内得到的由上向下观察物体的视图,叫做俯视图.
在侧面内得到的由左向右观察物体的视图,叫做左视图.
探究三视图的画法
(1)课件展示:如图①,对几何体进行正投影得到三视图.
(2)将水平面、侧面、正面展开到同一平面,观察得到的三种视图的位置关系.
(3)同桌讨论得到的三种视图在大小上的规律,如图②.
归纳:三个视图的大小是互相联系的,画三视图时,三个视图要放在正确的位置.并且使主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.
画图时规定:看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
师生活动:
①明了学情:关注学生是否理解用投影定义视图,是否理解用三种视图表示立体图形的意义.
②差异指导:对学生在探究过程中产生的疑惑适时点拨.
③生生互助:小组内交流、讨论,形成共识.
三、典例剖析
例1:画出下图所示的一些基本几何体的三视图.
分析:画这些基本几何体的三视图时,要注意从三个方向观察它们.具体画法为:
(1)确定主视图的位置,画出主视图;
(2)在主视图正下方画出俯视图,注意与主视图“长对正”.
(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”.
解:
例2:画出如图(1)所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
分析:支架的形状是由两个大小不等的长方体构成的组合体.画三视图时要注意这两个长方体的上下、前后位置关系.
解:如上图(2)所示,是支架的三视图.
师生活动:
学生独立思考、观察、解决例题,并与同伴交流,教师巡视,适当引导学生解决.
四、课堂小结
(1)本节课主要学习了哪些知识?重点研究了什么问题?
(2)通过这些内容的学习,你知道画一个物体的三视图的步骤吗?
教师强调:确定好三视图的位置,“长对正”“高平齐”“宽相等”.
五、检测反馈
1.下列几何体的主视图不是中心对称图形的是( B )
,A) ,B) ,C) ,D)
2.下面的几何体中,主视图为三角形的是( C )
,A) ,B) ,C) ,D)
3.在①长方体,②正方体,③圆锥,④圆柱,⑤三棱柱,⑥球,这六种几何体中,其主视图、左视图、俯视图都完全相同的是__②⑥__(填上序号即可).
六、课后作业
第四课时 由三视图描述几何体
1.会根据物体的三视图描述出几何体形状或实物原型.
2.经历探索简单几何体三视图来描述几何体的形状的过程,进一步发展空间想象能力.
根据物体的三视图想象出几何体的形状或实物原型.
由物体的三视图得到它的平面展开图的转化.
一、情景导入
问题1:请你找出图中所示物体所对应的主视图.
问题2:若一个物体的三视图都是圆,则这个物体是什么呢?
二、自学互研
阅读教材P98例3,完成下列问题:
1.由三视图想象立体图形时,要分别根据主视图、俯视图、左视图想象立体图形__正__面、__上__面、__左__面,然后再结合起来考虑整体图形.
2.一个立体图形的俯视图是圆,则这个图形可能是__圆锥、圆柱__.
3.其主视图、左视图与俯视图均相同的是__正方体和球__.
1.一个立体图形的三视图是一个正方形和两个长方形,则这个图形是( B )
A.正方体 B.长方体 C.四面体 D.四棱锥
2.如图,三视图所表示的物体是__五棱锥__.
3.根据下列物体的三视图,判断该几何体是__圆台__.
方法归纳:先看主视图和俯视图(或左视图),再综合左视图(或俯视图),根据几何体从三个角度观察得到的图形,综合得出几何体原形.
师生活动:
①明了学情:关注学生是否体会到由实物到视图的想象是“分”的过程,由视图到实物的想象是“合”的过程.
②差异指导:深入小组,对学生在探究中产生的疑惑及时引导与点拨.
③生生互助:学生小组内交流、讨论、相互解疑释难.
三、典例剖析
例1:根据下面的三视图说出立体图形的名称.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形.
解:(1)从三个方向看立体图形,视图都是矩形,可以想象这个立体图形是长方体,如下图(1)所示.
(2)从正面、侧面看立体图形,视图都是等腰三角形;从上面看,视图是圆;可以想象这个立体图形是圆锥,如下图(2)所示.
例2:根据物体的三视图(如下图),描述物体的形状.
分析:由主视图可知,物体正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到,另有两条棱(虚线表示)被遮挡;由左视图可知,物体左侧有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
解:物体是正五棱柱形状的,如下图所示:
师生活动:
学生独立观察,思考解决例题,然后小组内交流讨论,并积极主动到黑板展示,教师在巡视中对学生及时进行点拨.
四、课堂小结
(1)三视图的作用是什么?
(2)由三视图怎样想象出立体图形?
教师总结:(1)三视图可以表示立体图形;(2)根据主视图、俯视图和左视图分别想象立体图形的正面、上面和左面的形状,再综合起来想象它的整体形状.
五、检测反馈
1.一个几何体的三个视图如图所示,这个几何体是( A )
A.圆柱 B.球 C.圆锥 D.正方体
2.一张桌子摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上碟子共有( C )
A.9个 B.10个 C.12个 D.13个
3.如图①是一块带有圆形空洞和方形空洞的小木板,则图②所示的几何体中既可以堵住圆形空洞,又可以堵住方形空洞的是( B )
4.“横看成岭侧成峰,远近高低各不同”是从正面、侧面、高处往低处俯视,这三种角度看风景.如果一个实物正面看是三角形,侧面看也是三角形,上面看是带圆心的圆,那么这个实物是__圆锥__.
六、课后作业
第五课时 由三视图到展开图
1.能根据三视图想象出基本几何体的展开图.
2.在探究由三视图想象出立体图形的过程中,初步建立空间观念,发展几何直觉和形象思维 ,培养空间想象能力.
根据三视图描述基本几何体和实物原型及计算几何体的表面积等.
根据三视图想象出立体图形的表面展开图,计算立体图形的表面积、体积等.
一、情景导入
某工厂要加工一批密封罐,设计者给出了密封罐的三视图(如图),请按照三视图确定制作每个密封罐所需钢板的面积(图中尺寸单位:mm)
二、自学互研
阅读教材P99内容,解答例5提出的问题:
问题分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形——展开图.在实际生产中,三视图和展开图往往结合在一起使用.解决活动一中的问题的思路是先由三视图想象出密封罐的形状,再进一步画出展开图,然后计算面积.
解:由三视图可知,密封罐的形状是正六棱柱(如图①).
密封罐的高为50 mm,底面正六边形的直径为100 mm,边长为50 mm,图②是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为:
6×50×50+2×6××50×50sin60°
=6×502×
≈27990(mm2)
教师可给学生提供一个思路:解决本题的思路是先由视图想象出密封罐的立体形状,再进一步画出展开图,从而计算面积.
师生活动:
①明了学情:关注学生能否由三视图想象实物体,再画出实物展开图.
②差异指导:深入小组内对学生的疑惑及时引导、点拨.
③生生互助:小组内合作交流、相互解疑释难、达成共识.
三、典例剖析
例1:某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个茶叶罐所需钢板的面积.
解:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面直径为100,高为150.
因为每个密封罐所需钢板的面积即为该圆柱体的表面积,所以S=2π×502+2π×50×150=20000π.
例2:如图是由一些棱长为1 cm的正方体小木块搭建成的几何体的主视图、俯视图和左视图,请问:
(1)这个几何体是由多少个小木块组成的?
(2)在俯视图中标出相应位置小木块的个数;
(3)求出该几何体的表面积(包括底面).
分析:(1)由俯视图可得该组合几何体最底层的木块个数,由主视图或左视图可得第二层和第三层的小木块的个数,相加即可;
(2)根据上题得到的小木块的个数,在俯视图上标出来即可;
(3)将几何体的各个面的面积相加即可得到其表面积.
师生活动:
教师展示图片,由学生先独立思考、想象,再小组内探究体验,合作、交流、展示.
四、课堂小结
(1)本节课主要学习了哪些知识?
(2)对于本课时所学习的知识还存在哪些疑惑?
教师强调:三视图与平面展开图的相互转化:三视图——实物——平面展开图.
五、检测反馈
1.(杭州中考)已知某几何体的三视图(单位:cm)如图所示,则该几何体的侧面积等于( B )
A.12π cm2 B.15π cm2
C.24π cm2 D.30π cm2
,(第1题图)) ,(第2题图))
2.一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的表面积为( D )
A.2π B.6π
C.7π D.8π
3.如图是一个几何体的三视图,其中俯视图为正三角形,则这个几何体的侧面积是( A )
A.18 cm2 B.20 cm2
C.(18+2)cm2 D.(18+4)cm2
,(第3题图)) ,(第4题图))
4.如图是一个上下底密封纸盒的三视图,根据图中数据,可计算这个密封纸盒的表面积为__(75+360)__cm2(结果可保留根号).
六、课后作业
第六课时 制作立体模型
1.在实际动手活动中进一步加深对投影和视图知识的认识,加强在实践活动中手脑结合的能力.
2.通过制作模型,体会由平面图形转化为立体图形的过程与乐趣.
3.通过动手实践活动,培养学生的创新意识与发明创造意识.
让学生亲自经历规律的发现、深入、研究、应用的过程.
学生通过手工制作,实现理论与实践的结合.
一、情景导入
下列模型是如何得到的?
以上立体图形都是通过拼接平面图形得到的,如何制作平面图形,从而拼接得到立体图形呢?
二、自学互研
阅读“课题学习”,完成下列问题:
问题1:以硬纸板为主要材料,分别做出下面的两组三视图表示的立体模型.
问题2:按照下面给出的两组三视图,用马铃薯(或萝卜)做出相应的实物模型.
展示作品:教师展示学生的优秀作品,学生共同鉴赏评品.
师生活动:
教师提问,想一想上面两组三视图,分别表示什么实物模型?学生确定了实物模型的形状后,利用马铃薯动手制作,在制作过程中,教师强调安全、有序,确保活动顺利进行,学生制作完成后,教师展示课前制作好的模型样品,供学生参考、比较.
三、典例剖析
例:下面的每一组平面图形都是由四个等边三角形组成的.
(1)指出其中哪些可以折叠成多面体,并把上面的图形描在纸上,剪下来,叠一叠,验证你的答案;
(2)画出由上面图形能折叠成的多面体的三视图,并指出三视图中是怎样体现“长对正、高平齐、宽相等”的;
(3)如果上图中小三角形的边长为1,那么对应的多面体的体积和表面积各是多少?
解:(1)经过验证,图①②③都可以折成多面体.
(2)先确定能折叠成的多面体为三棱锥,其三视图如图所示.
(3)如果图中的小三角形的边长为1,那么对应的多面体的体积都是Sh=××1×1=,表面积都是×1×1×4=.
活动结论:
1.数学是以数量关系和空间形式为主要研究对象的学科,数量关系和空间形式是从现实世界中抽象出来的.投影和视图的知识是从实际需要(建筑、制造等)中产生的,它们与实际生活联系得非常紧密.
2.从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得出立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力是非常重要的.
四、课堂小结
通过本节课的学习,你有了哪些新的收获或疑问?
说出你的想法与同学们分享.
五、检测反馈
1.如图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是__①②④__(把正确的立体图形的序号都填在横线上).
2.如图中的图形是由一个扇形和一个圆组成的.
(1)把图中的图形描在纸上,剪下来,围成一个圆锥;
(2)画出图中的图形围成的圆锥的三视图;
(3)如果图中的扇形的半径为13,圆的半径为5,那么围成的圆锥的体积是多少?
解:(1)在纸片上用铅笔描出上面的图形,围成一个圆锥,如图所示.
(2)画出围成的圆锥的左视图、主视图、俯视图如图所示.
(3)如图所示,扇形的半径为13,圆的半径为5,在直角三角形中,圆锥的高度为=12,圆锥的体积V=Sh=×π×52×12=100π.
六、课后作业
第二十九章总结与提升
1.进一步理解投影、三视图等概念.
2.能画出几何体的三视图,能根据三视图想象物体的形状.
进一步加深对本章知识的理解,提高解题技能.
利用三视图想象实物形状,并根据相关数据进行计算.
一、情景导入
本章知识结构图:
二、自学互研
通阅本章内容,完成下列问题:
问题1:平行投影和中心投影的区别是什么?如何判别物体的投影是平行投影还是中心投影?
答:区别在于平行投影是在平行光线下形成的投影,而中心投影是在相交光线下形成的投影.区别这两种投影的关键是抓住光线的特征.
问题2:如图,晚上小明在路灯下散步,在小明由A处走到B处这一过程中,他在地上的影子( C )
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
问题3:下图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的左视图是( A )
,A) ,B) ,C) ,D)
问题4:如图是某种物体的三视图及相关数据(单位:cm),求该物体的体积(≈1.732,π=3.14,精确到0.01 cm3).
解:S底=6××0.8×=(cm2),V=×1-π(0.4)2×1=-≈≈1.16032≈1.16(cm3).
师生活动:
①明了学情:关注学生对本章知识的掌握与运用情况.
②差异指导:对探究中学生遗忘的知识及时引导与点拨.
③生生互助:小组合作、交流讨论、达成共识.
三、典例剖析
例1:如图是一个几何体的三视图,这个几何体的表面积为________(π取3.14).
解析:这个几何体是圆锥.圆锥的底面半径为1,母线长为2,所以圆锥的侧面积是×2π×2=2π,底面积是π,则表面积是2π+π=3π≈9.42.
答案:9.42
例2:用小正方体木块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗?它最少需要多少个小正方体木块?最多需要多少个小正方体木块?
解:这样的几何体不唯一,它最少需要10个小正方体木块,最多需要16个小正方体木块,其中,第一层7块,第二层至少2块,最多6块,第三层至少1块,最多3块.
俯视图中小方格内的数字表示所放的小正方体的最少如图(1),最多如图(2).
师生活动:
学生观察、思考、相互交流,进一步加强对本章重要知识点的理解与运用,老师巡视,适时对学生进行引导分析.
四、课堂小结
通过本节课学习,你对本章知识又有了哪些新的认识?还有什么疑惑?请说给老师和同学们听听?
五、检测反馈
1.如图放置的几何体的左视图是( C )
,A) ,B) ,C) ),\s\do5(D))
2.由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是( A )
A.3 B.4 C.5 D.6
3.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是__72__.
4.如图是某几何体的展开图.
(1)这个几何体的名称是;
(2)画出这个几何体的三视图;
(3)求出这个几何体的体积.(π取3.14)
解:(1)圆柱;
(2)三视图为:;
(3)体积为V=πr2h=3.14×52×20=1570.
六、课后作业
