第28章 圆 单元复习检测卷(含答案)
文档属性
| 名称 | 第28章 圆 单元复习检测卷(含答案) | 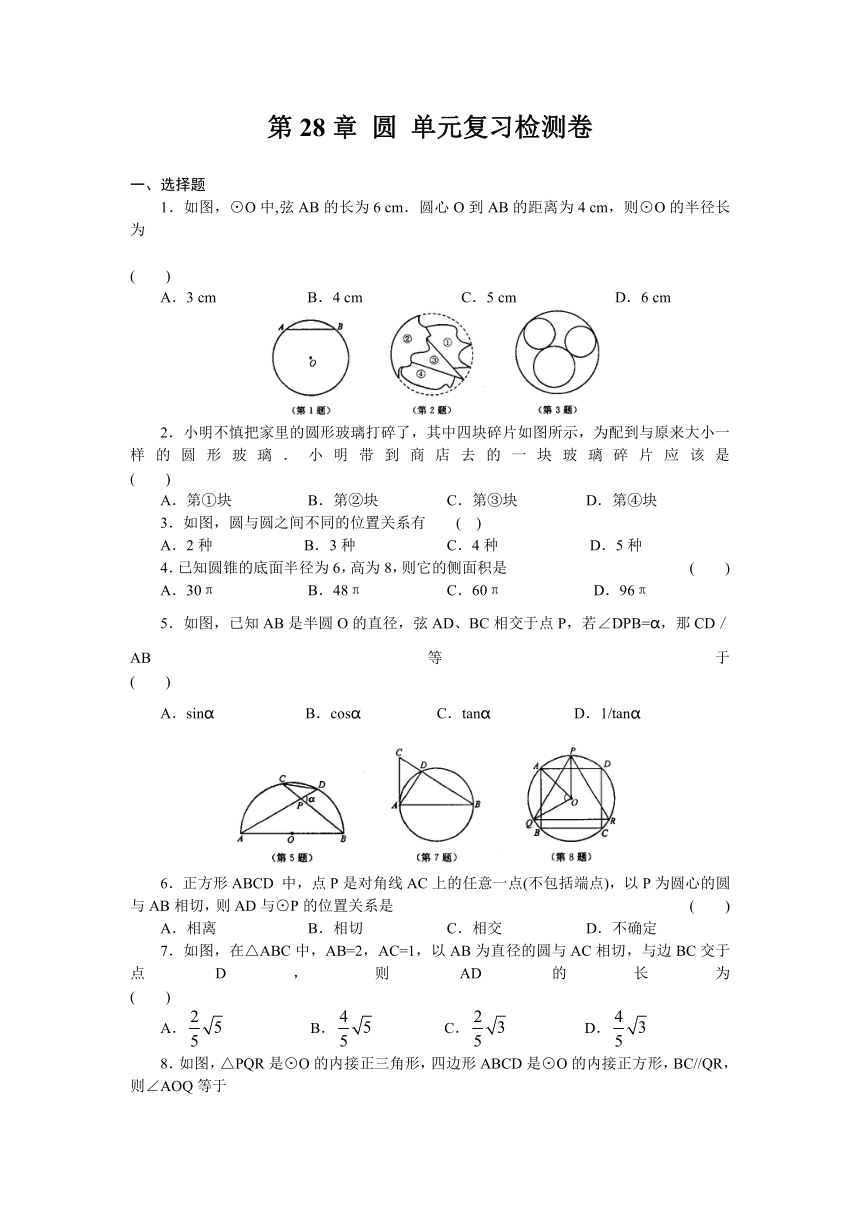 | |
| 格式 | zip | ||
| 文件大小 | 63.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-16 12:42:55 | ||
图片预览


文档简介
第28章 圆 单元复习检测卷
一、选择题
1.如图,⊙O中,弦AB的长为6 cm.圆心O到AB的距离为4 cm,则⊙O的半径长为
( )
A.3 cm B.4 cm C.5 cm D.6 cm
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃.小明带到商店去的一块玻璃碎片应该是 ( )
A.第①块 B.第②块 C.第③块 D.第④块
3.如图,圆与圆之间不同的位置关系有 ( )
A.2种 B.3种 C.4种 D.5种
4.已知圆锥的底面半径为6,高为8,则它的侧面积是 ( )
A.30π B.48π C.60π D.96π
5.如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那CD/AB等于 ( )
A.sinα B.cosα C.tanα D.1/tanα
6.正方形ABCD 中,点P是对角线AC上的任意一点(不包括端点),以P为圆心的圆与AB相切,则AD与⊙P的位置关系是 ( )
A.相离 B.相切 C.相交 D.不确定
7.如图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为 ( )
A. B. C. D.
8.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC//QR,则∠AOQ等于
A.60° B.65° C.72° D.75°
二、填空题
9.如图,A、B、C是⊙O上三点,∠ACB=40°,则∠ABO等于 。.
10.如图,⊙O是△ABC的外接圆,∠C=30°,AB=2 cm,则⊙O的半径为 cm.
11.如图,PA是⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OB=6,则tan∠APO
的值是 .
12.如图,PA、PB切⊙O于点A、B,点C是⊙O上一点,∠ACB=65°,则∠P= °.
13.已知扇形的半径为2 cm,面积是πcm2,则扇形的弧长是 cm,扇形的圆心
角为 °.
14.如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=8 cm,则图中阴影部分的面积为 cm2.
15.如图,点A、B是⊙O上两点.AB=10,点P是⊙O上的动点(P与A、B不重合),连结AP、PB,过点O分别作DE⊥AP于E,OF⊥PB于F,则EF= .
16.将一直径为1 7 cm的圆形纸片(图①)剪成如图②所示形状的纸片,再将纸片沿虚线
折叠得到正方体(图③)形状的纸盒,则这样的纸盒体积最大为 cm3.
三、解答题
17.如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
18.如图,在⊙O中,AB是直径,∠BOC=120°,PC是⊙O的切线,切点是C,点D在劣弧上运动.当∠CPD满足什么条件时,直线PD与直线AB垂直 证明你的结论.
19.如图,已知AB为⊙O的直径,直线BC与⊙O相切于点B,过A作AD//OC交⊙O
于点D,连结CD.
(1)求证:CD是⊙O的切线;
(2)若AD=2,直径AB=6,求线段BC的长.
20.如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与半圆O交于点E,连结BE、DE.
(1)求证:∠BED=∠C;
(2)若OA=5,AD=8,求AC的长.
21.如图,AB是⊙O的直径,∠BAC=60°,P是OB上一点,过P作AB的垂线与AC的延长线交于点Q,过点C的切线CD交PQ于D,连结OC.
(1)求证:△CDQ是等腰三角形;
(2)如果△CDQ≌△COB,求BP:PO的值.
22.如图(1),线段PB过圆心O,交圆O于A、B两点,PC切圆O于点C,作AD⊥PC,垂足为D,连结AC、BC.
(1)写出图(1)中所有相等的角(直角除外),并给出证明;
(2)若图(1)中的切线PC变为图(2)中割线PCE的情形,割线PCE与圈O交于C、E两
点,AE与BC交于点M,AD⊥PE,写出图(2)中相等的角(写出三组即可,直角除外);
(3)在图(2)中,证明AD·AB=AC·AE.
参考答案
l.C 2.B 3.C 4.C 5.B 6.B 7.A 8.D 9.80 10.2 11. 12.50 13. 120 14. 15.5 16.1 17.(1)连结OA ∵OC=BC,AC=OB,∴OC=BC= AC=OA,∴△ACO是等边三角形,故∠O=60°,又可得∠B=30°,∴∠OAB=90°,∴AB是⊙O的切线. (2)作AE⊥CD于E点 ∵∠O=60°, ∠D=30°,又∠ACD=45°,AC =OC=2,∴在Rt△ACE中,CE=AE=.在Rt△ADE中,∵∠D=30°,∴AD=.由勾股定理,可求DE= ∴CD=DE+CE=+ l8.当∠CPD=60°时.直线PD与直线AB垂直 证明:略 19.(1)如图,连结OD,
∵AD//OC,∴∠1=∠3,∠2=∠A, ∵OA=OD,∴∠3=∠A,∴∠1=∠2.
∵OD=OB,OC=OC, ∴△COD≌△COB.∵AB是⊙O直径,BC与
⊙O相切,∴∠CBO=90°, ∴在∠CDO=90°, ∴CD是⊙O的切线.
(2) 20.(1) ∵AC是⊙O的切线,AB是⊙O直径,
∴AB⊥AC,即∠1+∠2=90°.又∵OC⊥AD.∴∠1+∠C=90°.
∴∠C=∠2.而∠BED=∠2,∴∠BED=∠C. (2)AC=. 21.(1)由已知得∠ACB=90°,∠ABC=30°,∴∠Q=30°,∠BCO=
∠ABC=30°.∵CD⊙O的切线,CO是半径,∴CD⊥CO,∴∠DCQ=∠BCO=30°.∴∠DCQ=∠Q,故△CDQ是等腰三角形. (2)BP:PO= 22.(1)相等的角有:
∠ACD=∠ABC,∠BAC=∠CAD. 证明:略 (2) ∠ACD=∠ABE,∠ABC=∠AEC,∠BAE=∠BCE. (3) 易证△ADC∽AEB ∴ ∴AB·AB=AC·AE.
一、选择题
1.如图,⊙O中,弦AB的长为6 cm.圆心O到AB的距离为4 cm,则⊙O的半径长为
( )
A.3 cm B.4 cm C.5 cm D.6 cm
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃.小明带到商店去的一块玻璃碎片应该是 ( )
A.第①块 B.第②块 C.第③块 D.第④块
3.如图,圆与圆之间不同的位置关系有 ( )
A.2种 B.3种 C.4种 D.5种
4.已知圆锥的底面半径为6,高为8,则它的侧面积是 ( )
A.30π B.48π C.60π D.96π
5.如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那CD/AB等于 ( )
A.sinα B.cosα C.tanα D.1/tanα
6.正方形ABCD 中,点P是对角线AC上的任意一点(不包括端点),以P为圆心的圆与AB相切,则AD与⊙P的位置关系是 ( )
A.相离 B.相切 C.相交 D.不确定
7.如图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为 ( )
A. B. C. D.
8.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC//QR,则∠AOQ等于
A.60° B.65° C.72° D.75°
二、填空题
9.如图,A、B、C是⊙O上三点,∠ACB=40°,则∠ABO等于 。.
10.如图,⊙O是△ABC的外接圆,∠C=30°,AB=2 cm,则⊙O的半径为 cm.
11.如图,PA是⊙O的切线,A为切点,PO交⊙O于点B,PA=8,OB=6,则tan∠APO
的值是 .
12.如图,PA、PB切⊙O于点A、B,点C是⊙O上一点,∠ACB=65°,则∠P= °.
13.已知扇形的半径为2 cm,面积是πcm2,则扇形的弧长是 cm,扇形的圆心
角为 °.
14.如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=8 cm,则图中阴影部分的面积为 cm2.
15.如图,点A、B是⊙O上两点.AB=10,点P是⊙O上的动点(P与A、B不重合),连结AP、PB,过点O分别作DE⊥AP于E,OF⊥PB于F,则EF= .
16.将一直径为1 7 cm的圆形纸片(图①)剪成如图②所示形状的纸片,再将纸片沿虚线
折叠得到正方体(图③)形状的纸盒,则这样的纸盒体积最大为 cm3.
三、解答题
17.如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
18.如图,在⊙O中,AB是直径,∠BOC=120°,PC是⊙O的切线,切点是C,点D在劣弧上运动.当∠CPD满足什么条件时,直线PD与直线AB垂直 证明你的结论.
19.如图,已知AB为⊙O的直径,直线BC与⊙O相切于点B,过A作AD//OC交⊙O
于点D,连结CD.
(1)求证:CD是⊙O的切线;
(2)若AD=2,直径AB=6,求线段BC的长.
20.如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与半圆O交于点E,连结BE、DE.
(1)求证:∠BED=∠C;
(2)若OA=5,AD=8,求AC的长.
21.如图,AB是⊙O的直径,∠BAC=60°,P是OB上一点,过P作AB的垂线与AC的延长线交于点Q,过点C的切线CD交PQ于D,连结OC.
(1)求证:△CDQ是等腰三角形;
(2)如果△CDQ≌△COB,求BP:PO的值.
22.如图(1),线段PB过圆心O,交圆O于A、B两点,PC切圆O于点C,作AD⊥PC,垂足为D,连结AC、BC.
(1)写出图(1)中所有相等的角(直角除外),并给出证明;
(2)若图(1)中的切线PC变为图(2)中割线PCE的情形,割线PCE与圈O交于C、E两
点,AE与BC交于点M,AD⊥PE,写出图(2)中相等的角(写出三组即可,直角除外);
(3)在图(2)中,证明AD·AB=AC·AE.
参考答案
l.C 2.B 3.C 4.C 5.B 6.B 7.A 8.D 9.80 10.2 11. 12.50 13. 120 14. 15.5 16.1 17.(1)连结OA ∵OC=BC,AC=OB,∴OC=BC= AC=OA,∴△ACO是等边三角形,故∠O=60°,又可得∠B=30°,∴∠OAB=90°,∴AB是⊙O的切线. (2)作AE⊥CD于E点 ∵∠O=60°, ∠D=30°,又∠ACD=45°,AC =OC=2,∴在Rt△ACE中,CE=AE=.在Rt△ADE中,∵∠D=30°,∴AD=.由勾股定理,可求DE= ∴CD=DE+CE=+ l8.当∠CPD=60°时.直线PD与直线AB垂直 证明:略 19.(1)如图,连结OD,
∵AD//OC,∴∠1=∠3,∠2=∠A, ∵OA=OD,∴∠3=∠A,∴∠1=∠2.
∵OD=OB,OC=OC, ∴△COD≌△COB.∵AB是⊙O直径,BC与
⊙O相切,∴∠CBO=90°, ∴在∠CDO=90°, ∴CD是⊙O的切线.
(2) 20.(1) ∵AC是⊙O的切线,AB是⊙O直径,
∴AB⊥AC,即∠1+∠2=90°.又∵OC⊥AD.∴∠1+∠C=90°.
∴∠C=∠2.而∠BED=∠2,∴∠BED=∠C. (2)AC=. 21.(1)由已知得∠ACB=90°,∠ABC=30°,∴∠Q=30°,∠BCO=
∠ABC=30°.∵CD⊙O的切线,CO是半径,∴CD⊥CO,∴∠DCQ=∠BCO=30°.∴∠DCQ=∠Q,故△CDQ是等腰三角形. (2)BP:PO= 22.(1)相等的角有:
∠ACD=∠ABC,∠BAC=∠CAD. 证明:略 (2) ∠ACD=∠ABE,∠ABC=∠AEC,∠BAE=∠BCE. (3) 易证△ADC∽AEB ∴ ∴AB·AB=AC·AE.
