2.4 绝对值 课件

2.4 绝对值
讲授新课
课堂小结
导入新课
当堂练习
教学过程
1
理解绝对值的概念，会求一个数的绝对值。
重点
2
理解绝对值的意义，掌握求有理数的绝对值的方法，体会数形结合的思想方法。
重点
3
会利用绝对值比较两个负数的大小。
难点
学习目标
2、数轴的三要素
1、什么是数轴？

温故而知新
0
1
2
-1
-2
规定了原点、正方向和单位长度的直线叫做数轴。
原点、正方向、单位长度
温故而知新
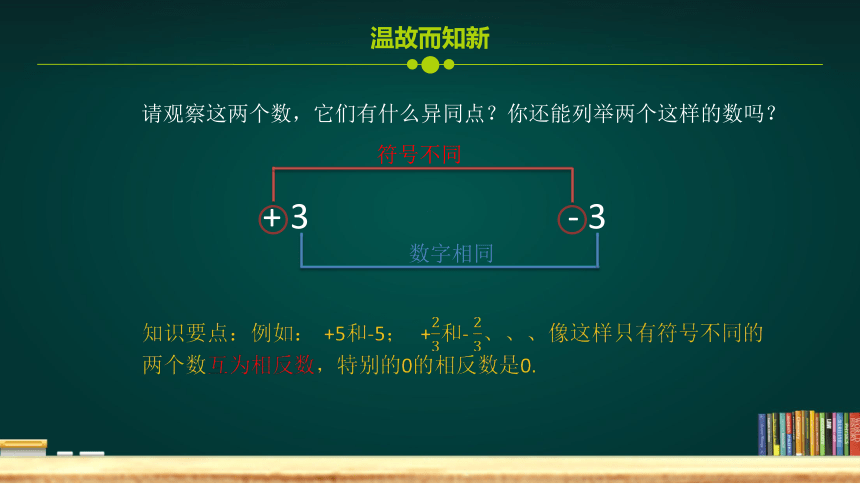
请观察这两个数，它们有什么异同点？你还能列举两个这样的数吗？
+ 3
- 3
符号不同
数字相同
?
情境引入
0
1
2
3
4
-1
-2
-3
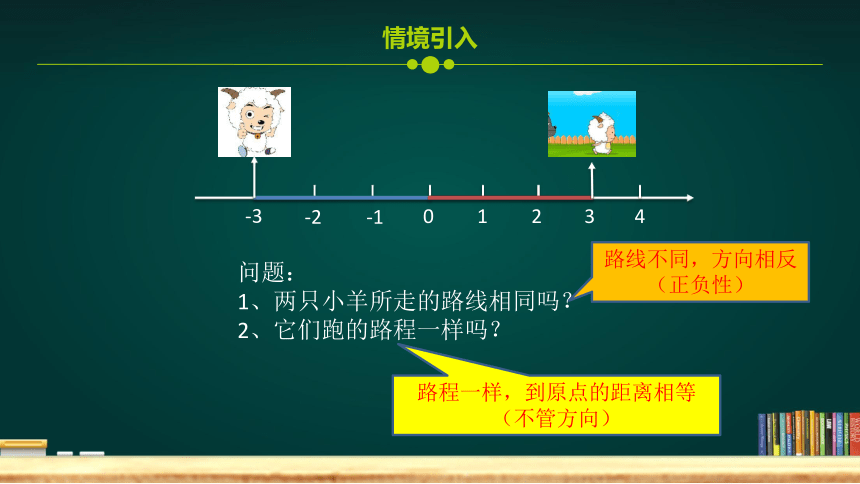
问题：
1、两只小羊所走的路线相同吗？
2、它们跑的路程一样吗？
路线不同，方向相反（正负性）
路程一样，到原点的距离相等（不管方向）
情境引入
0
1
2
3
4
-1
-2
-3
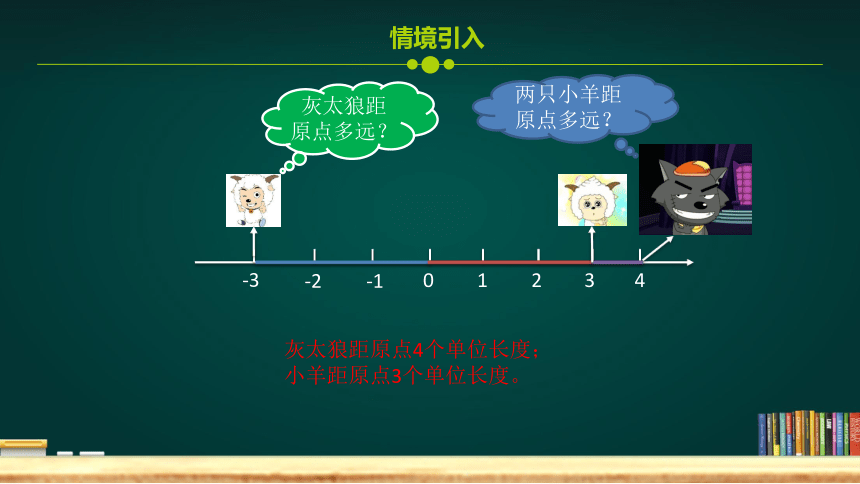
灰太狼距原点多远？
两只小羊距原点多远？
灰太狼距原点4个单位长度；
小羊距原点3个单位长度。
新知讲解
知识要点：我们把在数轴上表示数a的点到原点的距离叫做数a的绝对值，用“ a ”表示。
-3
-4
-2
-1
0
1
2
3
4
-4到原点的距离是4，所以-4的绝对值是4，记作 -4 =4.
0到原点的距离是0，所以0的绝对值是0，记作 0 =0.
3到原点的距离是3，所以3的绝对值是3，记作 3 =3.
距离没有负数
试一试：-4的绝对值是多少？3的绝对值是多少？0的绝对值呢？
1
相等
互为相反数的两个数的绝对值有什么关系？
2
分类讨论：
正数、负数、和0
一个数的绝对值与这个数有什么关系？
议一议
?
?
规律总结
结论1：正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值是0.
结论2：任何一个有理数的绝对值都是非负数，即对于任意有理数a，总有：a ≥0. （非负性）
转化成数学语言：
（1）如果a>0，那么 a =a；
（2）如果a=0，那么 a =0；
（3）如果a<0，那么 a =-a.
课堂小练
判断：
1、绝对值最小的数是0。（ ）
2、一个数的绝对值一定是正数。（ ）
3、一个数的绝对值不可能是负数。（ ）
4、一个数的绝对值越大，表示它的点在数轴上离原点越近。（ ）
对
错
对
错
课堂小练
（1）绝对值是7的数有几个？各是什么？有没有绝对值是-2的数？
答：绝对值小于3的整数一共有5个，分别是： -2、-1、 0、 1、 2.
答：绝对值是0的数有1个，就是0
答：绝对值是7的数有两个，各是7与-7，没有绝对值是-2的数。
（2）绝对值是0的数有几个？各是什么？
（3）绝对值小于3的整数一共有多少个？
抢答：
合作探究
探究如何比较两个负数的大小：
（1）在数轴上表示下列两个数，并比较它们的大小
-3、 -5
0
1
2
-1
-2
-3
-4
-5
.
.
-5
-3
-5＜-3
（2）求出（1）中两个数的绝对值，并比较他们的大小。
?
（3）通过（1）（2）你发现了什么？
结论：两个负数比较大小，绝对值大的反而小。
课堂小练
?
?
课堂小结
绝对值
绝对值的定义
绝对值的性质
比较两个负数的大小
在数轴上表示数的点到原点的距离
?
?
绝对值大的反而小
当堂检测
?
≥0
0
1
±4
-6
7.2
Thank You