人教版八年级数学上册14. 1.4 整式的乘法(3)多项式乘多项式 课件(共19张ppt)
文档属性
| 名称 | 人教版八年级数学上册14. 1.4 整式的乘法(3)多项式乘多项式 课件(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览






文档简介
单项式与单项式相乘的法则:
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
复习备用
单项式与多项式相乘的法则:
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
复习备用
x(x 2 – zy2 )= .
x 3 – xzy2
( x + y)(x 2 – zy2 )= ?
人教版八年级数学上册
第十四章 整式的乘法与因式分解
14.1.4 整式的乘法
(3)多项式乘多项式
1.能运用多项式与多项式相乘的法则进行简单的运算
2.在多项式与多项式相乘的运算中,进一步熟悉幂的运算性质、单项式的乘法及单项式与多项式的乘法法则,增强综合运算能力.
重点:多项式与多项式相乘的法则及利用法则进行运算.
难点:多项式与多项式相乘的法则的应用.
学习目标
重点难点
先学后教
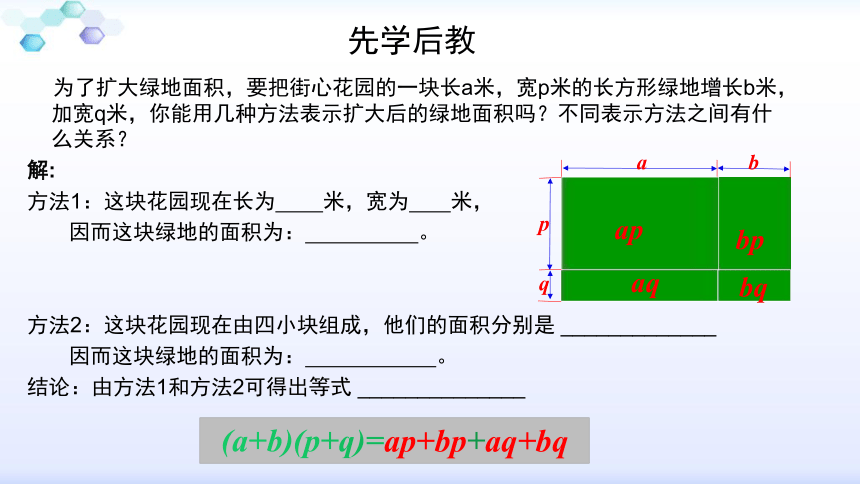
为了扩大绿地面积,要把街心花园的一块长a米,宽p米的长方形绿地增长b米,加宽q米,你能用几种方法表示扩大后的绿地面积吗?不同表示方法之间有什么关系?
解:
方法1:这块花园现在长为 米,宽为 米,
因而这块绿地的面积为: 。
方法2:这块花园现在由四小块组成,他们的面积分别是 _____________
因而这块绿地的面积为: 。
结论:由方法1和方法2可得出等式 ______________
p
b
a
q
ap
bp
aq
bq
(a+b)(p+q)=ap+bp+aq+bq
归纳总结
知识点一:多项式与多项式相乘
(a+b)(p+q)=ap+aq+bp+bq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
检测
知识点一:多项式与多项式相乘
1.下列变式正确的是( )
D.(x-1)(x-2)=x·x + x·(-2)+(-1)·x +(-1)×(-2)
A.(x-1)(x-2)=x·x +(-1)×(-2)
B.(x-1)(x-2)=x·x + x·(-2)+(-1)×(-2)
C.(x-1)(x-2)=x·x + x·2 + 1·x +1×2
D
2 (1)(x+2)(x?3), (2)(3x -1)(2x+1)。
解:
(1) (x+2)(x?3)
?
3x
+2 x
=
x2 -x-6
-2×3
(2) (3x -1)(2x+1)
=
=x﹒x
3x?2x
+3x? 1
-1?2 x
?
1
=
6x2
+3x
-2 x
?1
=
6x2 +x?1.
负负得正
负正得负
注意:
1.两项相乘时,先定符号。所得积的符号由这两项的符号来确定:
2.最后的结果要合并同类项,结果化为最简形式
检测
(1) (-2m-1)(3m-2)
(2) (x + 2y)2
分析:先弄清楚两个多项式中的每一项
分析:先将(x + 2y)2变式为(x + 2y) (x + 2y)
解:原式=(-2m)·3m+(-2m)·(-2)+(-1)·3m +(-1)×(-2)
= -6m2 + 4m +(-3m) + 2
= -6m2 + m + 2
解:原式=(x + 2y) (x + 2y)
= x·x + x·2y + 2y·x + 2y·2y
= x2 + 2xy + 2xy + 4y2
= x2 + 4xy + 4y2
注意每一项的符号,特别是负号时不要遗漏
结果有同类项的要合并同类项
检测
3.如果(x-2)(x+1)= x2 + mx + n,求 m + n的值.
分析:根据多项式乘多项式法则把等式的左边展开,根据题意求出m、n的值,计算即可。
(x-2)(x+1)
= x·x + x·1 + (-2)·x + (-2)×1
= x2 + x + (-2x) + (-2)
= x2– x - 2
解:由题意得,
∴ m = -1 n = -2
∴ m + n =(-1)+(-2)= -3
故 m + n 的值为-3.
∵ x2 + mx + n = x2– x - 2
检测
归纳总结
知识点一:多项式与多项式相乘
(1)先用一个多项式的每一项分别乘以另一个多项式的每一项;
(2)把各乘积相加;
(3)有同类项的要合并同类项;
(4)通常把结果整理成按某一字母的降幂排列.
多项式与多项式相乘的步骤:
知识点二:多项式乘以多项式法则的应用
检测
若(x+a)(x-2)的积中不含x的一次项,则a的值是 .
解: (x+a)(x-2)=x2﹣2x+ax﹣2a
= x2+(a﹣2)x﹣2a
由题意可知:a﹣2=0
∴ a=2
知识点二:多项式乘以多项式法则的应用
检测
先化简,再求值:(3x+1)(2x﹣3)﹣(6x﹣5)(x﹣4),其中 x=﹣2.
解: 原式=6x2﹣7x﹣3﹣(6x2﹣29x+20)
= 6x2﹣7x﹣3﹣6x2+29x﹣20
=22x﹣23
当 x=﹣2时,原式= 22×(﹣2)﹣23=﹣67
计算下列各式,然后回答问题:
① (x+2)(x+3)= ② (x-4)(x+1)=
③ (y+4)(y-2)= ④ (y-5)(y-3)=
观察上述式子,你可以 得出一个什么规律吗?
(x+p)(x+q) =
x2 + 5x+6;
x2–3x-4
y2 +2y-8
y2-8y+15
x2 + (p+q) x + p q
知识点三:(x+p)(x+q)=x2+(p+q)x+pq
当堂训练
1.(2018武汉)计算(a﹣2)(a+3)的结果是( )
A.a2﹣6 B.a2+a﹣6 C.a2+6 D.a2﹣a+6
2.如果(x-3)(x+4)=x2+px+q,那么p,q的值是( )
A.p=1,q=﹣12 B.p=﹣1,q=12
C.p=7,q=12 D.p=7,q=﹣12
3.下列多项式相乘的结果为x2+3x﹣18的是( )
A.(x-2)(x+9) B.(x+2)(x﹣9) C.(x+3(x﹣6) D.(x﹣3(x+6)
B
A
D
当堂训练
1.计算(a-2)(a+3)的结果是( )
A.a2-6 B.a2+a-6 C.a2+6 D.a2-a+6
2.下列计算错误的是( )
A.(x+1)(x+4)=x2+5x+4 B.(y+4)(y﹣5)=y2+9y﹣20
C.(m﹣2)(m+3)=m2+m﹣6 D.(x﹣3)(x﹣6)=x2﹣9x+18
3.若(x+2)(x﹣1)=x2+mx+n,则m +n=( )
A.1 B.-2 C.﹣1 D.2
B
B
C
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3)
答案: (1) 2x2+7x+3; (2) m2+5mn+6n2;
(3) a2-2a+1; (4) a2-9b2
(5) x2+5x+6; (6) x2-3x-4;
(7) y2+2y-8; (8) y2-8y+15.
当堂训练
思维导图
1.课本第102页练习以及习题14.1第5、8、14、15题
作业布置
单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
复习备用
单项式与多项式相乘的法则:
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
复习备用
x(x 2 – zy2 )= .
x 3 – xzy2
( x + y)(x 2 – zy2 )= ?
人教版八年级数学上册
第十四章 整式的乘法与因式分解
14.1.4 整式的乘法
(3)多项式乘多项式
1.能运用多项式与多项式相乘的法则进行简单的运算
2.在多项式与多项式相乘的运算中,进一步熟悉幂的运算性质、单项式的乘法及单项式与多项式的乘法法则,增强综合运算能力.
重点:多项式与多项式相乘的法则及利用法则进行运算.
难点:多项式与多项式相乘的法则的应用.
学习目标
重点难点
先学后教
为了扩大绿地面积,要把街心花园的一块长a米,宽p米的长方形绿地增长b米,加宽q米,你能用几种方法表示扩大后的绿地面积吗?不同表示方法之间有什么关系?
解:
方法1:这块花园现在长为 米,宽为 米,
因而这块绿地的面积为: 。
方法2:这块花园现在由四小块组成,他们的面积分别是 _____________
因而这块绿地的面积为: 。
结论:由方法1和方法2可得出等式 ______________
p
b
a
q
ap
bp
aq
bq
(a+b)(p+q)=ap+bp+aq+bq
归纳总结
知识点一:多项式与多项式相乘
(a+b)(p+q)=ap+aq+bp+bq
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
检测
知识点一:多项式与多项式相乘
1.下列变式正确的是( )
D.(x-1)(x-2)=x·x + x·(-2)+(-1)·x +(-1)×(-2)
A.(x-1)(x-2)=x·x +(-1)×(-2)
B.(x-1)(x-2)=x·x + x·(-2)+(-1)×(-2)
C.(x-1)(x-2)=x·x + x·2 + 1·x +1×2
D
2 (1)(x+2)(x?3), (2)(3x -1)(2x+1)。
解:
(1) (x+2)(x?3)
?
3x
+2 x
=
x2 -x-6
-2×3
(2) (3x -1)(2x+1)
=
=x﹒x
3x?2x
+3x? 1
-1?2 x
?
1
=
6x2
+3x
-2 x
?1
=
6x2 +x?1.
负负得正
负正得负
注意:
1.两项相乘时,先定符号。所得积的符号由这两项的符号来确定:
2.最后的结果要合并同类项,结果化为最简形式
检测
(1) (-2m-1)(3m-2)
(2) (x + 2y)2
分析:先弄清楚两个多项式中的每一项
分析:先将(x + 2y)2变式为(x + 2y) (x + 2y)
解:原式=(-2m)·3m+(-2m)·(-2)+(-1)·3m +(-1)×(-2)
= -6m2 + 4m +(-3m) + 2
= -6m2 + m + 2
解:原式=(x + 2y) (x + 2y)
= x·x + x·2y + 2y·x + 2y·2y
= x2 + 2xy + 2xy + 4y2
= x2 + 4xy + 4y2
注意每一项的符号,特别是负号时不要遗漏
结果有同类项的要合并同类项
检测
3.如果(x-2)(x+1)= x2 + mx + n,求 m + n的值.
分析:根据多项式乘多项式法则把等式的左边展开,根据题意求出m、n的值,计算即可。
(x-2)(x+1)
= x·x + x·1 + (-2)·x + (-2)×1
= x2 + x + (-2x) + (-2)
= x2– x - 2
解:由题意得,
∴ m = -1 n = -2
∴ m + n =(-1)+(-2)= -3
故 m + n 的值为-3.
∵ x2 + mx + n = x2– x - 2
检测
归纳总结
知识点一:多项式与多项式相乘
(1)先用一个多项式的每一项分别乘以另一个多项式的每一项;
(2)把各乘积相加;
(3)有同类项的要合并同类项;
(4)通常把结果整理成按某一字母的降幂排列.
多项式与多项式相乘的步骤:
知识点二:多项式乘以多项式法则的应用
检测
若(x+a)(x-2)的积中不含x的一次项,则a的值是 .
解: (x+a)(x-2)=x2﹣2x+ax﹣2a
= x2+(a﹣2)x﹣2a
由题意可知:a﹣2=0
∴ a=2
知识点二:多项式乘以多项式法则的应用
检测
先化简,再求值:(3x+1)(2x﹣3)﹣(6x﹣5)(x﹣4),其中 x=﹣2.
解: 原式=6x2﹣7x﹣3﹣(6x2﹣29x+20)
= 6x2﹣7x﹣3﹣6x2+29x﹣20
=22x﹣23
当 x=﹣2时,原式= 22×(﹣2)﹣23=﹣67
计算下列各式,然后回答问题:
① (x+2)(x+3)= ② (x-4)(x+1)=
③ (y+4)(y-2)= ④ (y-5)(y-3)=
观察上述式子,你可以 得出一个什么规律吗?
(x+p)(x+q) =
x2 + 5x+6;
x2–3x-4
y2 +2y-8
y2-8y+15
x2 + (p+q) x + p q
知识点三:(x+p)(x+q)=x2+(p+q)x+pq
当堂训练
1.(2018武汉)计算(a﹣2)(a+3)的结果是( )
A.a2﹣6 B.a2+a﹣6 C.a2+6 D.a2﹣a+6
2.如果(x-3)(x+4)=x2+px+q,那么p,q的值是( )
A.p=1,q=﹣12 B.p=﹣1,q=12
C.p=7,q=12 D.p=7,q=﹣12
3.下列多项式相乘的结果为x2+3x﹣18的是( )
A.(x-2)(x+9) B.(x+2)(x﹣9) C.(x+3(x﹣6) D.(x﹣3(x+6)
B
A
D
当堂训练
1.计算(a-2)(a+3)的结果是( )
A.a2-6 B.a2+a-6 C.a2+6 D.a2-a+6
2.下列计算错误的是( )
A.(x+1)(x+4)=x2+5x+4 B.(y+4)(y﹣5)=y2+9y﹣20
C.(m﹣2)(m+3)=m2+m﹣6 D.(x﹣3)(x﹣6)=x2﹣9x+18
3.若(x+2)(x﹣1)=x2+mx+n,则m +n=( )
A.1 B.-2 C.﹣1 D.2
B
B
C
(1) (2x+1)(x+3); (2) (m+2n)(m+ 3n):
(3) ( a - 1)2 ; (4) (a+3b)(a –3b ).
(5) (x+2)(x+3); (6) (x-4)(x+1)
(7) (y+4)(y-2); (8) (y-5)(y-3)
答案: (1) 2x2+7x+3; (2) m2+5mn+6n2;
(3) a2-2a+1; (4) a2-9b2
(5) x2+5x+6; (6) x2-3x-4;
(7) y2+2y-8; (8) y2-8y+15.
当堂训练
思维导图
1.课本第102页练习以及习题14.1第5、8、14、15题
作业布置
