人教版八年级数学上册14.1.4单项式乘以多项式练习课件(共20张ppt)
文档属性
| 名称 | 人教版八年级数学上册14.1.4单项式乘以多项式练习课件(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 451.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览





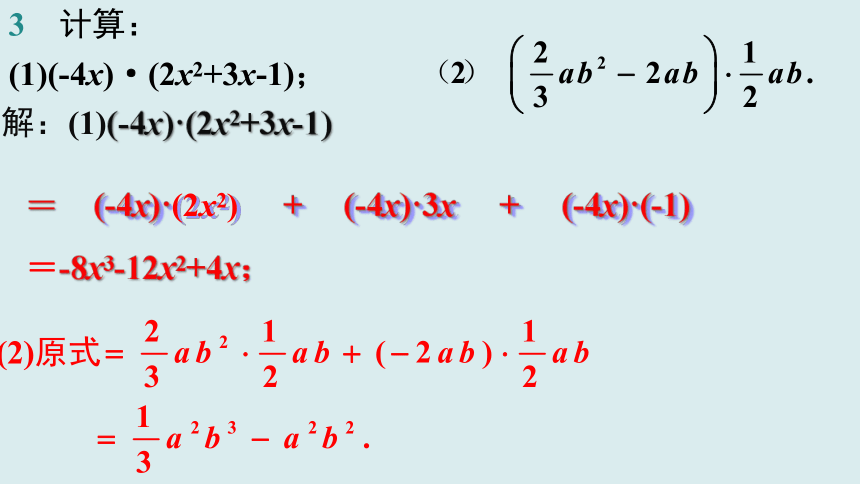
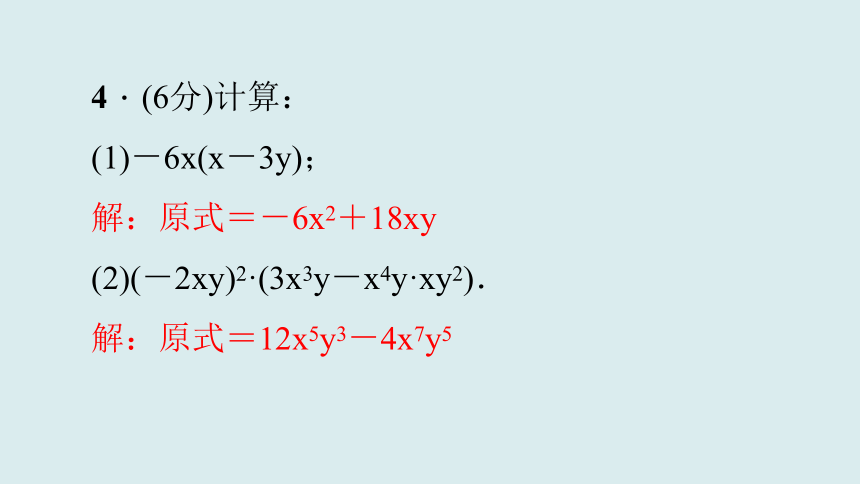
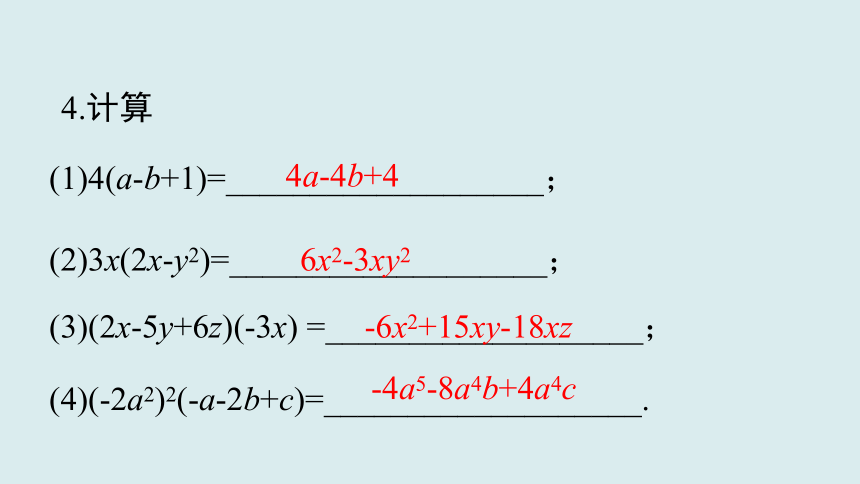
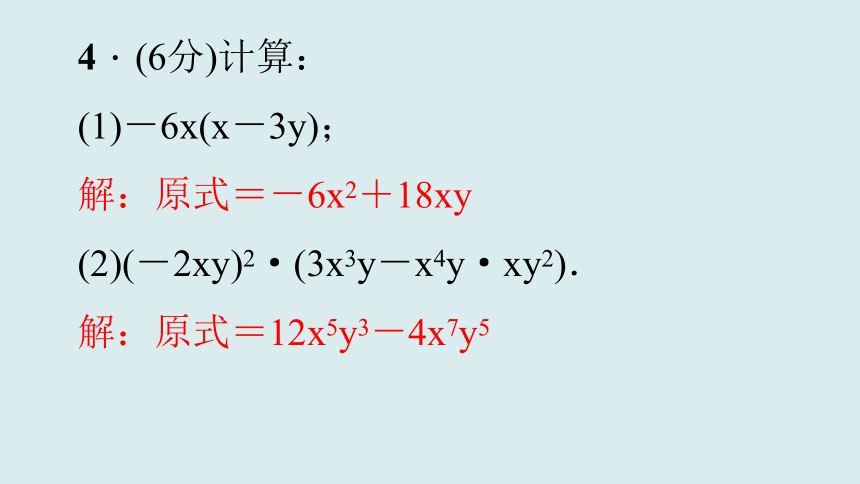
文档简介
单项式与多项式相乘,就是用单项式去乘多项式的___________,
再把_________________.
每一项
所得的积相加
1.(3分)(2017·台湾)计算6x·(3-2x)的结果,与下列哪一个式子相同( )
A.-12x2+18x B.-12x2+3
C.16x D.6x
2.(3分)若一个长方体的长、宽、高分别为2x,x,3x-4,
则长方体的体积为( )
A.3x3-4x2 B.6x2-8x
C.6x3-8x2 D.6x3-8x
A
C
1.计算 3a2·2a3的结果是( )
A.5a5 B.6a5 C.5a6 D.6a6
2.计算(-9a2b3)·8ab2的结果是( )
A.-72a2b5 B.72a2b5 C.-72a3b5 D.72a3b5
3.若(ambn)·(a2b)=a5b3 那么m+n=( )
A.8 B.7 C.6 D.5
B
C
D
B
3 计算:
(1)(-4x)·(2x2+3x-1);
解:(1)(-4x)·(2x2+3x-1)
=
=-8x3-12x2+4x;
(-4x)·(2x2)
(-4x)·3x
(-4x)·(-1)
+
+
(2)原式
4.(6分)计算:
(1)-6x(x-3y);
解:原式=-6x2+18xy
(2)(-2xy)2·(3x3y-x4y·xy2).
解:原式=12x5y3-4x7y5
(1)4(a-b+1)=___________________;
4a-4b+4
(2)3x(2x-y2)=___________________;
6x2-3xy2
(3)(2x-5y+6z)(-3x) =___________________;
-6x2+15xy-18xz
(4)(-2a2)2(-a-2b+c)=___________________.
-4a5-8a4b+4a4c
4.计算
4.(6分)计算:
(1)-6x(x-3y);
解:原式=-6x2+18xy
(2)(-2xy)2·(3x3y-x4y·xy2).
解:原式=12x5y3-4x7y5
5.(6分)先化简,再求值:3a(a2-2a+1)-2a2(a-3),其中a=2.
解:原式=a3+3a,当a=2时,原式=14
4 先化简,再求值:3a(2a2-4a+3)-2a2(3a+4)其中a=-2.
当a=-2时,
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
原式=-20×4-9×2=-98.
D
如果(-3x)2(x2-2nx+2)的展开式中不含x3项,求n的值.
方法总结:在整式乘法的混合运算中,要注意运算顺序.注意当要求多项式中不含有哪一项时,则表示这一项的系数为0.
解:(-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
∵展开式中不含x3项,∴n=0.
解:原式=3a3b2-3a2b3-3a2b2-2a3b2+3a2b3-2a2b2=a3b2-5a2b2
8.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到的答案是x2-2x+1,那么正确的计算结果是多少?
解:设这个多项式为A,则
∴A=4x2-2x+1.
∴A·(-3x2)=(4x2-2x+1)(-3x2)
A+(-3x2)=x2-2x+1,
=-12x4+6x3-3x2.
解:5x2+5x-15-24x-4x2-x2+4x=0,-15x=15,x=-1
5.计算:-2x2·(xy+y2)-5x(x2y-xy2).
解 原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
6.解方程:8x(5-x)=34-2x(4x-3).
解得 x=1.
解:去括号,得40x-8x2=34-8x2+6x,
移项,得40x-6x=34,
合并同类项,得 34x=34,
再把_________________.
每一项
所得的积相加
1.(3分)(2017·台湾)计算6x·(3-2x)的结果,与下列哪一个式子相同( )
A.-12x2+18x B.-12x2+3
C.16x D.6x
2.(3分)若一个长方体的长、宽、高分别为2x,x,3x-4,
则长方体的体积为( )
A.3x3-4x2 B.6x2-8x
C.6x3-8x2 D.6x3-8x
A
C
1.计算 3a2·2a3的结果是( )
A.5a5 B.6a5 C.5a6 D.6a6
2.计算(-9a2b3)·8ab2的结果是( )
A.-72a2b5 B.72a2b5 C.-72a3b5 D.72a3b5
3.若(ambn)·(a2b)=a5b3 那么m+n=( )
A.8 B.7 C.6 D.5
B
C
D
B
3 计算:
(1)(-4x)·(2x2+3x-1);
解:(1)(-4x)·(2x2+3x-1)
=
=-8x3-12x2+4x;
(-4x)·(2x2)
(-4x)·3x
(-4x)·(-1)
+
+
(2)原式
4.(6分)计算:
(1)-6x(x-3y);
解:原式=-6x2+18xy
(2)(-2xy)2·(3x3y-x4y·xy2).
解:原式=12x5y3-4x7y5
(1)4(a-b+1)=___________________;
4a-4b+4
(2)3x(2x-y2)=___________________;
6x2-3xy2
(3)(2x-5y+6z)(-3x) =___________________;
-6x2+15xy-18xz
(4)(-2a2)2(-a-2b+c)=___________________.
-4a5-8a4b+4a4c
4.计算
4.(6分)计算:
(1)-6x(x-3y);
解:原式=-6x2+18xy
(2)(-2xy)2·(3x3y-x4y·xy2).
解:原式=12x5y3-4x7y5
5.(6分)先化简,再求值:3a(a2-2a+1)-2a2(a-3),其中a=2.
解:原式=a3+3a,当a=2时,原式=14
4 先化简,再求值:3a(2a2-4a+3)-2a2(3a+4)其中a=-2.
当a=-2时,
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
原式=-20×4-9×2=-98.
D
如果(-3x)2(x2-2nx+2)的展开式中不含x3项,求n的值.
方法总结:在整式乘法的混合运算中,要注意运算顺序.注意当要求多项式中不含有哪一项时,则表示这一项的系数为0.
解:(-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
∵展开式中不含x3项,∴n=0.
解:原式=3a3b2-3a2b3-3a2b2-2a3b2+3a2b3-2a2b2=a3b2-5a2b2
8.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到的答案是x2-2x+1,那么正确的计算结果是多少?
解:设这个多项式为A,则
∴A=4x2-2x+1.
∴A·(-3x2)=(4x2-2x+1)(-3x2)
A+(-3x2)=x2-2x+1,
=-12x4+6x3-3x2.
解:5x2+5x-15-24x-4x2-x2+4x=0,-15x=15,x=-1
5.计算:-2x2·(xy+y2)-5x(x2y-xy2).
解 原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
6.解方程:8x(5-x)=34-2x(4x-3).
解得 x=1.
解:去括号,得40x-8x2=34-8x2+6x,
移项,得40x-6x=34,
合并同类项,得 34x=34,
