人教版七年级数学下册教学课件-5.1.3同位角、内错角、同旁内角(共20张ppt)
文档属性
| 名称 | 人教版七年级数学下册教学课件-5.1.3同位角、内错角、同旁内角(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 19:49:08 | ||
图片预览






文档简介
5.1.3同位角、内错角、同旁内角
团结 求实 创新 奉献
B
F
E
A
O
1
3
2
4
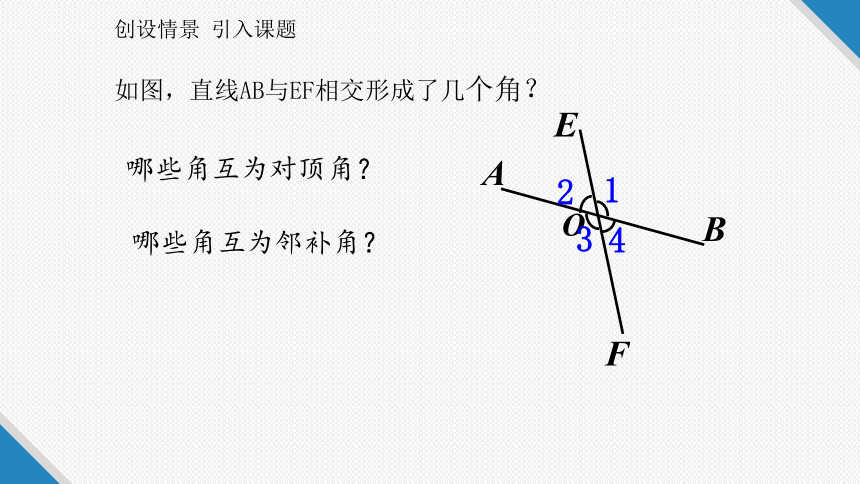
如图,直线AB与EF相交形成了几个角?
哪些角互为邻补角?
哪些角互为对顶角?
创设情景 引入课题
B
F
E
2
3
1
4
A
O
C
D
6
7
5
8
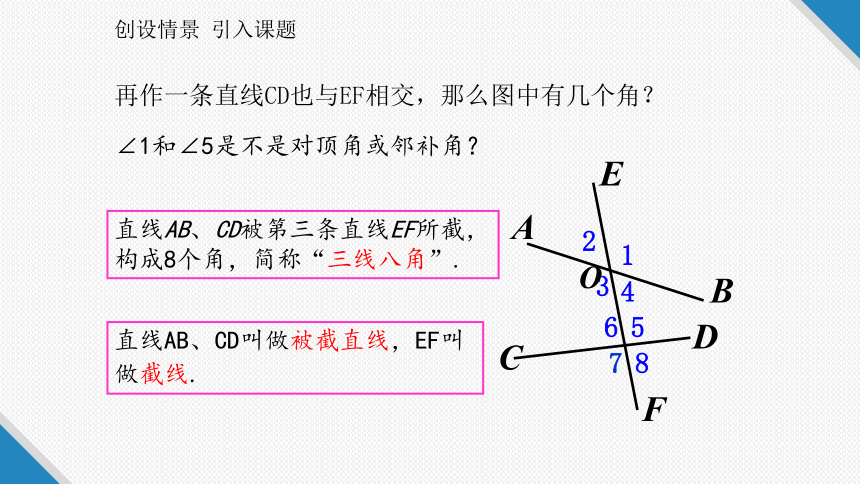
再作一条直线CD也与EF相交,那么图中有几个角?
∠1和∠5是不是对顶角或邻补角?
直线AB、CD叫做被截直线,EF叫做截线.
直线AB、CD被第三条直线EF所截,构成8个角,简称“三线八角”.
创设情景 引入课题
观察图中∠1和∠5,它们有什么样的位置特征?
都在直线EF的
1
5
⌒
⌒
图中除了∠1和∠5,还有同位角吗?
在直线AB、CD的
同位角:
∠2和∠6 ∠3和∠7 ∠4和∠8
师生协作 生成概念(同位角)
特点:
右侧
上方
两角的公共边是截线
形如字母F
同侧
同方
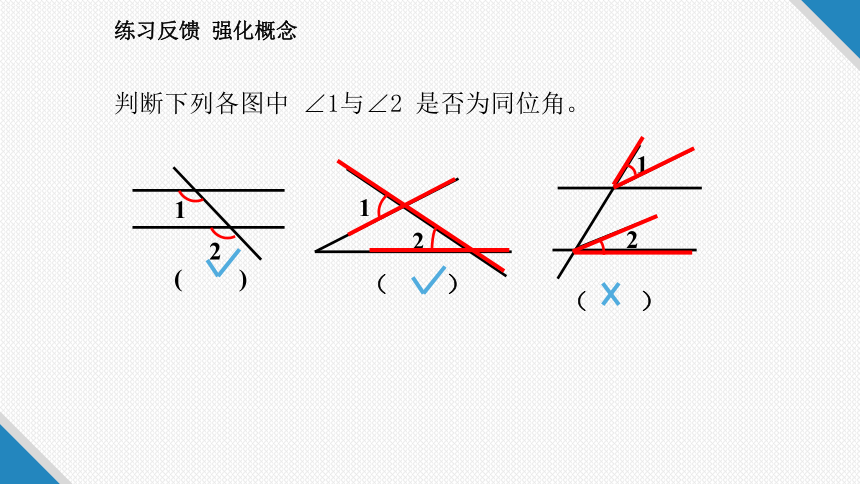
判断下列各图中 ∠1与∠2 是否为同位角。
1
2
( )
1
2
( )
( )
1
2
练习反馈 强化概念
图中∠3和∠5是不是同位角?它们有什么样的位置特征?
图中除了∠3和∠5,还有内错角吗?
内错角
师生协作 生成概念(内错角)
∠4和∠6
3
5
⌒
⌒
特点:
在直线EF的
在直线AB和CD
两侧
之间
两角的公共边是截线
形如字母Z
下列图形中∠1,∠2是否为内错角?
(1)
(2)
2
1
⌒
⌒
是
不是
练习反馈 强化概念
2
1
⌒
⌒
(3)
是
1
2
观察图中∠3和∠6的位置,它们有什么样的位置特征?
图中除了∠3和∠6,还有同旁内角吗?
⌒
5
⌒
4
同旁内角
师生协作 生成概念(同旁内角)
∠4和∠5
特点:
都在直线EF的
在直线AB和CD
左侧
之间
两角的公共边是截线
形如字母U
同侧
下列图形中∠1,∠2是否为同旁内角?
(1)
(3)
(2)
2
1
⌒
⌒
2
1
⌒
⌒
⌒
⌒
1
2
是
是
不是
练习反馈 强化概念
请你指出下列图中的同位角,内错角,同旁内角
2
1
3
5
4
6
8
7
2、如图直线AB、CD被直线EF所截,则∠3的同位角是( )
A、∠1 B、∠2
C、∠3 D、∠4
3
⌒
4
⌒
2
⌒
5
⌒
1
⌒
A
E
B
C
D
F
A
练习反馈 强化概念
(2)若DE ,BF被AB所截,
则∠1与∠2是 。
同位角
(1)若DE,BC被AF所截,
则∠3与∠4是 。
内错角
练习反馈 强化概念
3.填空
(3)∠1与∠3是AB和AF被
所截构成的 。
DE
内错角
(4)∠2与∠AFB是AB和AF被
所截构成的 。
BC
同旁内角
练习反馈 强化概念
1
2
E
D
A
C
B
4.找出图中∠1的同旁内角
练习反馈 强化概念
1
2
E
D
A
C
B
图中与∠1是同旁内角的角:
1
E
D
A
C
B
1
A
C
B
1
2
A
C
B
练习反馈 强化概念
课堂小结 升华提高
角的名称
与被截直线的关系
与截线的关系
基本图形
图形结构特征
同位角
内错角
同旁内角
本节课你学到了什么?
被截直线
的同一方
被截直线
之间
被截直线
之间
截线的同侧
截线的两侧
截线的同侧
形如字母“F”(或倒置)
形如字母“Z”
(或反置)
形如字母“U”
你知道吗,将左、右手的大拇指和食指各组成一个角,两食指相对成一条直线,两个大拇指反向的时候就组成了一对角(如图1所示);两食指相对成一条直线,两个大拇指同向的时候又组成了一对角(如图2所示).
很有意思吧!
实践活动
Page
联系生活 开拓教学空间
作业布置
Page
课本第7页练习1、2题;
课本第11页习题5.1第11题。
5.1.3同位角、内错角、同旁内角
请大家批评指正,谢谢大家!
团结 求实 创新 奉献
B
F
E
A
O
1
3
2
4
如图,直线AB与EF相交形成了几个角?
哪些角互为邻补角?
哪些角互为对顶角?
创设情景 引入课题
B
F
E
2
3
1
4
A
O
C
D
6
7
5
8
再作一条直线CD也与EF相交,那么图中有几个角?
∠1和∠5是不是对顶角或邻补角?
直线AB、CD叫做被截直线,EF叫做截线.
直线AB、CD被第三条直线EF所截,构成8个角,简称“三线八角”.
创设情景 引入课题
观察图中∠1和∠5,它们有什么样的位置特征?
都在直线EF的
1
5
⌒
⌒
图中除了∠1和∠5,还有同位角吗?
在直线AB、CD的
同位角:
∠2和∠6 ∠3和∠7 ∠4和∠8
师生协作 生成概念(同位角)
特点:
右侧
上方
两角的公共边是截线
形如字母F
同侧
同方
判断下列各图中 ∠1与∠2 是否为同位角。
1
2
( )
1
2
( )
( )
1
2
练习反馈 强化概念
图中∠3和∠5是不是同位角?它们有什么样的位置特征?
图中除了∠3和∠5,还有内错角吗?
内错角
师生协作 生成概念(内错角)
∠4和∠6
3
5
⌒
⌒
特点:
在直线EF的
在直线AB和CD
两侧
之间
两角的公共边是截线
形如字母Z
下列图形中∠1,∠2是否为内错角?
(1)
(2)
2
1
⌒
⌒
是
不是
练习反馈 强化概念
2
1
⌒
⌒
(3)
是
1
2
观察图中∠3和∠6的位置,它们有什么样的位置特征?
图中除了∠3和∠6,还有同旁内角吗?
⌒
5
⌒
4
同旁内角
师生协作 生成概念(同旁内角)
∠4和∠5
特点:
都在直线EF的
在直线AB和CD
左侧
之间
两角的公共边是截线
形如字母U
同侧
下列图形中∠1,∠2是否为同旁内角?
(1)
(3)
(2)
2
1
⌒
⌒
2
1
⌒
⌒
⌒
⌒
1
2
是
是
不是
练习反馈 强化概念
请你指出下列图中的同位角,内错角,同旁内角
2
1
3
5
4
6
8
7
2、如图直线AB、CD被直线EF所截,则∠3的同位角是( )
A、∠1 B、∠2
C、∠3 D、∠4
3
⌒
4
⌒
2
⌒
5
⌒
1
⌒
A
E
B
C
D
F
A
练习反馈 强化概念
(2)若DE ,BF被AB所截,
则∠1与∠2是 。
同位角
(1)若DE,BC被AF所截,
则∠3与∠4是 。
内错角
练习反馈 强化概念
3.填空
(3)∠1与∠3是AB和AF被
所截构成的 。
DE
内错角
(4)∠2与∠AFB是AB和AF被
所截构成的 。
BC
同旁内角
练习反馈 强化概念
1
2
E
D
A
C
B
4.找出图中∠1的同旁内角
练习反馈 强化概念
1
2
E
D
A
C
B
图中与∠1是同旁内角的角:
1
E
D
A
C
B
1
A
C
B
1
2
A
C
B
练习反馈 强化概念
课堂小结 升华提高
角的名称
与被截直线的关系
与截线的关系
基本图形
图形结构特征
同位角
内错角
同旁内角
本节课你学到了什么?
被截直线
的同一方
被截直线
之间
被截直线
之间
截线的同侧
截线的两侧
截线的同侧
形如字母“F”(或倒置)
形如字母“Z”
(或反置)
形如字母“U”
你知道吗,将左、右手的大拇指和食指各组成一个角,两食指相对成一条直线,两个大拇指反向的时候就组成了一对角(如图1所示);两食指相对成一条直线,两个大拇指同向的时候又组成了一对角(如图2所示).
很有意思吧!
实践活动
Page
联系生活 开拓教学空间
作业布置
Page
课本第7页练习1、2题;
课本第11页习题5.1第11题。
5.1.3同位角、内错角、同旁内角
请大家批评指正,谢谢大家!
