人教版数学八年级 上册14.3.2公式法---平方差公式课件(共22张ppt)
文档属性
| 名称 | 人教版数学八年级 上册14.3.2公式法---平方差公式课件(共22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 19:49:55 | ||
图片预览







文档简介
14.3.2 因式分解公式法
——平方差
点击添加文本
点击添加文本
点击添加文本
点击添加文本
回顾 & 思考
?
请让我来了解你
1.什么是因式分解?
把一个多项式化成几个整式的 的形式.
积
×
×
√
2.判断下列变形过程,哪些是因式分解?
( )
( )
( )
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
情景引入
你能帮老师算一下吗?
(1)我家里有一张正方形的书桌,边长为1.21米,上面铺了一张边长为0.21米的正方形的桌垫(如图),我想知道桌垫未盖住的部分面积是多少?
1.21
(2)由于我家的书房太小,于是我请木工师傅把书桌变为边长为y米的正方形,那铺上桌垫后,未盖住的部分面积是多少?
0.21
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
(1) 下列多项式中,它们有什么共同特征?
(2)你能把它们写成因式乘积的形式吗?
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
整式乘法
因式分解
互逆
两个数的平方差,等于这两个数的和与这两个数的差的积。(P116)
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
2? 2= ( ) ( )
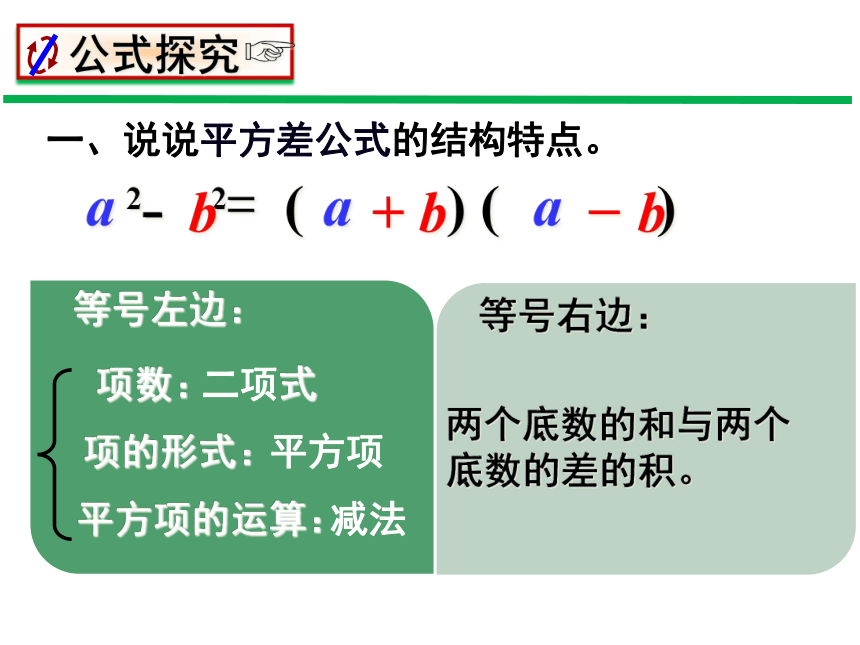
一、说说平方差公式的结构特点。
a
a
? b
+ b
a
b
二项式
平方项
减法
两个底数的和与两个底数的差的积。
等号左边:
项数:
项的形式:
平方项的运算:
等号右边:
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
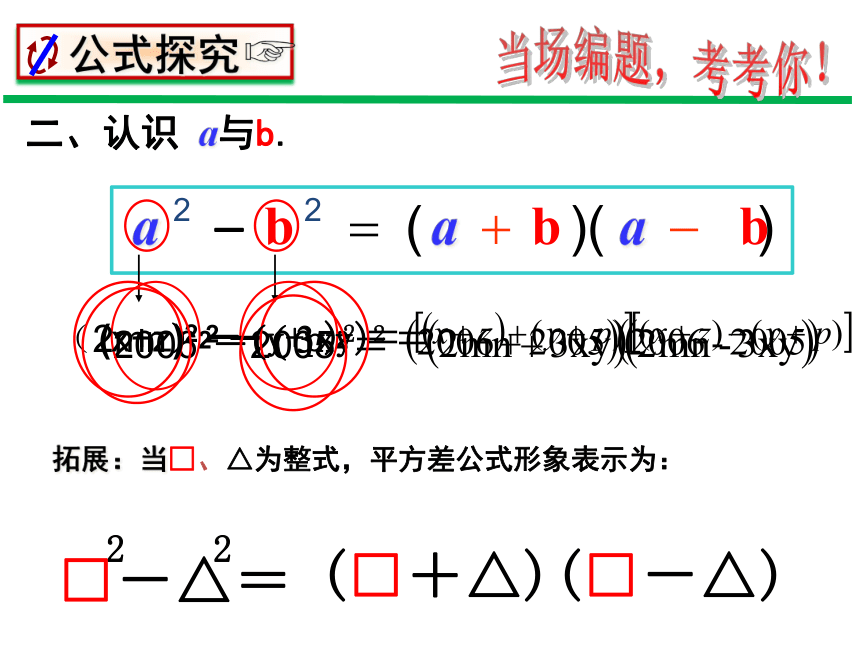
二、认识 a与b.
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
20062-20052 =
(2mn)2 - ( 3xy)2 =
(x+z)2 - (y+p)2 =
拓展:当□、△为整式,平方差公式形象表示为:
2
2
□-△=
(□+△)(□-△)
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
三、认识平方项前符号关系.
下列多项式能否用平方差公式来分解因式?为什么?
不能
能
能
不能
能
可利用平方差公式因式分解的多项式特征:
(1)两项;
(2)两项为或可化为平方项;
(3)两平方项异号。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例1:利用平方差分解因式.
□-△
2
2
先转化为
解:原式
错误!
注意:系数改写成某个数的
平方,从而形成某个整式的
完全平方。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例1:分解因式.
□-△
2
2
先转化为
注意:整体时必添括号。
解:原式
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例2:分解因式.
注意:分解彻底。
解:原式
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
分解因式.
变式例题
解:原式
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题反思
因式分解的顺序:
(1)提取公因式.
(2)找或转化 形式.
(3)用平方差公式。
(4)写几个因式的积的形式。
注意:检查分解因式要彻底。必须进行到每一个多项式因式不能再分解为止。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
应用公式
分解因式。
看谁做得最快最正确!
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
合作交流
1.出题:每个小组出一个能用平方差公式因式分解的多项式。
2.做题:1、2组,3、4组,5、6组,7、8组交换题目完成。
3.改题:完成后交回检查纠错。
小组完成后,小组长举手示意。看哪个小组又快又准确?
4.展示:请小组代表说出你设计的高妙之处,和你完成他组题目的解题步骤。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
合作交流
=(1.21+0.21)(1.21-0.21)
=1.42×1
=1.42
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
课堂小结
1.本节课你学会了什么?
2.在这节课中我们渗透了什么数学
思想与方法?
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例1:利用平方差分解因式.
解:
□-△
2
2
先转化为
错误!
注意:系数改写成某个数的平方。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例1:分解因式.
□-△
2
2
先转化为
解:
注意:整体时必添括号。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
作业布置
248-1可以被60到70之间的某两个整数整除,则这两个数为( )
A.61和63
B.63和65
C.65和67
D.67和69
B
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
课堂小结
1、运用平方差公式a2?b2= (a+b)(a?b)分解因式。
2、分解因式顺序:
3、在探索新知的过程,用到了整体、转化等数学思想和方法,体现了数学来源于数学,并用于生活。
首先提取公因式 然后考虑用公式 最终必是连乘式
——平方差
点击添加文本
点击添加文本
点击添加文本
点击添加文本
回顾 & 思考
?
请让我来了解你
1.什么是因式分解?
把一个多项式化成几个整式的 的形式.
积
×
×
√
2.判断下列变形过程,哪些是因式分解?
( )
( )
( )
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
情景引入
你能帮老师算一下吗?
(1)我家里有一张正方形的书桌,边长为1.21米,上面铺了一张边长为0.21米的正方形的桌垫(如图),我想知道桌垫未盖住的部分面积是多少?
1.21
(2)由于我家的书房太小,于是我请木工师傅把书桌变为边长为y米的正方形,那铺上桌垫后,未盖住的部分面积是多少?
0.21
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
(1) 下列多项式中,它们有什么共同特征?
(2)你能把它们写成因式乘积的形式吗?
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
整式乘法
因式分解
互逆
两个数的平方差,等于这两个数的和与这两个数的差的积。(P116)
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
2? 2= ( ) ( )
一、说说平方差公式的结构特点。
a
a
? b
+ b
a
b
二项式
平方项
减法
两个底数的和与两个底数的差的积。
等号左边:
项数:
项的形式:
平方项的运算:
等号右边:
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
二、认识 a与b.
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
20062-20052 =
(2mn)2 - ( 3xy)2 =
(x+z)2 - (y+p)2 =
拓展:当□、△为整式,平方差公式形象表示为:
2
2
□-△=
(□+△)(□-△)
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
公式探究
三、认识平方项前符号关系.
下列多项式能否用平方差公式来分解因式?为什么?
不能
能
能
不能
能
可利用平方差公式因式分解的多项式特征:
(1)两项;
(2)两项为或可化为平方项;
(3)两平方项异号。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例1:利用平方差分解因式.
□-△
2
2
先转化为
解:原式
错误!
注意:系数改写成某个数的
平方,从而形成某个整式的
完全平方。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例1:分解因式.
□-△
2
2
先转化为
注意:整体时必添括号。
解:原式
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例2:分解因式.
注意:分解彻底。
解:原式
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
分解因式.
变式例题
解:原式
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题反思
因式分解的顺序:
(1)提取公因式.
(2)找或转化 形式.
(3)用平方差公式。
(4)写几个因式的积的形式。
注意:检查分解因式要彻底。必须进行到每一个多项式因式不能再分解为止。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
应用公式
分解因式。
看谁做得最快最正确!
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
合作交流
1.出题:每个小组出一个能用平方差公式因式分解的多项式。
2.做题:1、2组,3、4组,5、6组,7、8组交换题目完成。
3.改题:完成后交回检查纠错。
小组完成后,小组长举手示意。看哪个小组又快又准确?
4.展示:请小组代表说出你设计的高妙之处,和你完成他组题目的解题步骤。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
合作交流
=(1.21+0.21)(1.21-0.21)
=1.42×1
=1.42
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
课堂小结
1.本节课你学会了什么?
2.在这节课中我们渗透了什么数学
思想与方法?
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例1:利用平方差分解因式.
解:
□-△
2
2
先转化为
错误!
注意:系数改写成某个数的平方。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
例题展示
例1:分解因式.
□-△
2
2
先转化为
解:
注意:整体时必添括号。
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
作业布置
248-1可以被60到70之间的某两个整数整除,则这两个数为( )
A.61和63
B.63和65
C.65和67
D.67和69
B
点击添加文本
点击添加文本
点击添加文本
点击添加文本
?
课堂小结
1、运用平方差公式a2?b2= (a+b)(a?b)分解因式。
2、分解因式顺序:
3、在探索新知的过程,用到了整体、转化等数学思想和方法,体现了数学来源于数学,并用于生活。
首先提取公因式 然后考虑用公式 最终必是连乘式
