人教版数学八年级上册15.1.2探究分式的基本性质课件(共38张ppt)
文档属性
| 名称 | 人教版数学八年级上册15.1.2探究分式的基本性质课件(共38张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览









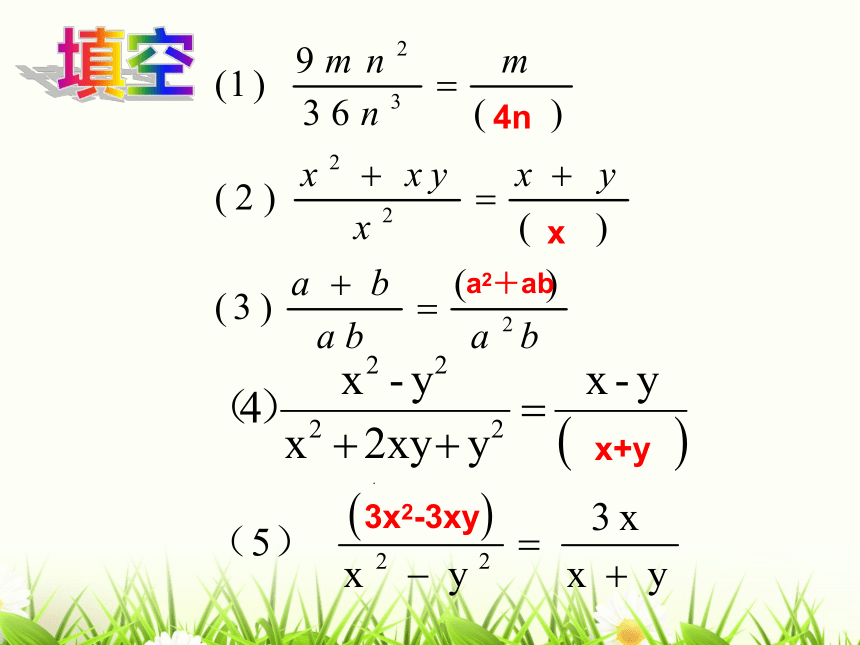


文档简介
15.1.2 分式的基本性质
2、分式有意义:
3、分式的值为零:
x取何值时,分式 有意义.
x取何值时,分式 的值为零.
X=-2
X≠ ±2
复习回顾
1、分式的概念:
(1) 下列各式中,属于分式的是( )
A、 B、 C、 D、
B
下列两式成立吗?为什么?
分数的分子与分母同时乘以(或除以)一个不等于0的数,分数的值不变.
分数的基本性质:
即;对于任意一个分数 有:
类比探究
思考
类比分数的基本性质,你能得到分式的基本性质吗?说说看!
一辆匀速行驶的汽车,
如果th行驶 skm,那么汽车的速度为 km/h。
如果2th行驶2 skm,那么汽车的速度为 km/h。
如果3th行驶3 skm,那么汽车的速度为 km/h。
如果nth行驶 nskm,那么汽车的速度为 km/h。
这些分式相等吗?为什么?
类比得到,分式的基本性质:
分式的分子与分母都乘以(或除以)同一个不等于0的整式 ,分式的值不变.
例1? 下列等式的右边是怎样从左边得到的?
(1)
∵ ,
∴ .
(2)
为什么本题未给 ?
(2)
解: (1)
∵
∴
下列各组分式,能否由左边变形为右边?
(1) 与
反思: 运用分式的基本性质应注意什么?
①“都”
②“同一个”
③ “不为0”
(2) 与
(3) 与
(4)
不能
不能
能
能
(5)
不能
2ab-b2
例2:填空
(1)看分母如何变化,想分子如何变化;
(2)看分子如何变化,想分母如何变化;
你是怎么想的?
.
4n
x
a2+ab
填空
3x2-3xy
x+y
例2 不改变分式的值,使下列分式的分子和分母都不含“-”号:
分式符号变换的依据与分数符号变换
的依据相同,也遵循“同号得正,异号得负”的原则。
规律总结
1、不改变分式的值,把分子或分母中多项式的第一项都不含“-”号.
解:
拓展练习
1.若把分式
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
的 x 和 y 都扩大两倍,则分式的值( )
2.若把分式 中的 和 都扩大3倍,那么分式
的值( ).
A.扩大3倍 B.扩大9倍
C.扩大4倍 D.不变
B
A
分数的约分和通分在分数的运算中起着重要的作用,类似的,分式的约分和通分在分式的运算中也起着重要的作用。
与分数类似:根据分式的基本性质,也可以对分式进 行约分和通分.
注意
分析:分式的约分,即要求把分子与分母的公因式约去,为此,首先要找出分子与分母的公因式.
例题
约去系数的最大公约数,和分子分母相同字母的最低次幂
先把分子、分母分别分解因式,然后约去公因式.
约分:
在化简分式 时,小颖和小明的做法出现了分歧:
小颖:
小明:
你对他们俩的解法有何看法?说说看!
彻底约分后的分式叫最简分式.
一般约分要彻底, 使分子、分母没有公因式.
辨别对错
做一做
1、约分 :
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去相同字母的最低次幂;
注意:约分过程中,有时还需运用分式的符号法则使最后结果形式简捷;约分的依据是分式的基本性质。
规律总结:
(3)化简分式时通常要使结果成为最简分式或整式.
(2)若分子﹑分母含有多项式,则先将多项式
分解因式,然后约去分子﹑分母中所有的公因式;
约分的基本步骤:
观察与思考:
类比计算:
结论:
异分母的分式相加减,必须先通分。
化成同分母的分式。
通分的概念
根据分数的基本性质 , 异分母的分数可化为同分母的分数 , 这一过程叫做分数的通分 .
类似的,
根据分式的基本性质 , 异分母的分式可化为同分母的分式,这一过程叫做分式的通分 .
分式的通分:
把几个异分母的分式化成与原来的
分式相等的同分母的分式的变形,
叫做分式的通分。
议一议
(1)求分式
的最简公分母。
12
系数:各分母系数的最小公倍数。
因式:各分母所有因式的最高次幂。
三个分式的最简公分母为12x3y4z。
确定最简公分母的方法:
类型一、分母都是单项式时,
(1)定系数________________
(2)定字母_________
(3)定字母的次数_______
这样取出的因式的积,就是最简公分母
练一练
确定下列各组分式的最简公分母:
解:
最简公分母是
通分:
试确定下列分式的最简公分母:
最简公分母是:xy(x-y)2(x+y)
(分母中虽然有的因式是多项式,但仍然是积的形式。)
确定最简公分母的方法:
类型二、有多项式分母时:
先对多项式进行_______,把含 字母的因式看作一个整体,然后再执行:
(1)定系数________________
(2)定字母(或含字母的因式)______________________
(3)定字母(或含字母的因式)的次数_________
(2) 与
1.确定分式的最简公分母。
2.求商式(最简公分母除以各个分母,得 到的商式)
3.利用分式基本性质通分.
分式通分的步骤:
反思拓展
例题学习
把下列分式通分
尝试练习一:
通分
练习2
把下列分式通分
检测与练习:
A、12xyz B、12x3y4z C、24xyz D、24x3y4z
B
3、通分:
本节课学习了哪些内容?
1.什么是分式的基本性质?
分式的分子与分母乘(或除以)同一个不等于0的整式 ,分式的值不变.
2. 运用分式的基本性质应注意什么?
(1)分子、分母应同时做乘、除法中的同一种运算;
(2)所乘(或除以)的必须是同一个整式;
(3)所乘(或除以)的整式应该不等于零.
3、分式的约分 最简分式
4、分式的通分运算中, 它的意义是怎样的?通分运算的关键是什么?
把几个异分母的分式,分别化成与原来分式相等的同分母的分式,叫做分式的通分。 通分的关键是确定几个分式的公分母,
确定最简公分母的方法:
(1)将各个分式的分母分解因式;
(2)各分母系数的最小公倍数。
(3)各分母所含有的因式。
(4)各分母所含相同因式的最高次幂。
(5)所得的系数与各字母(或因式)的最高次幂的积(其中系数都取正数)
2、分式有意义:
3、分式的值为零:
x取何值时,分式 有意义.
x取何值时,分式 的值为零.
X=-2
X≠ ±2
复习回顾
1、分式的概念:
(1) 下列各式中,属于分式的是( )
A、 B、 C、 D、
B
下列两式成立吗?为什么?
分数的分子与分母同时乘以(或除以)一个不等于0的数,分数的值不变.
分数的基本性质:
即;对于任意一个分数 有:
类比探究
思考
类比分数的基本性质,你能得到分式的基本性质吗?说说看!
一辆匀速行驶的汽车,
如果th行驶 skm,那么汽车的速度为 km/h。
如果2th行驶2 skm,那么汽车的速度为 km/h。
如果3th行驶3 skm,那么汽车的速度为 km/h。
如果nth行驶 nskm,那么汽车的速度为 km/h。
这些分式相等吗?为什么?
类比得到,分式的基本性质:
分式的分子与分母都乘以(或除以)同一个不等于0的整式 ,分式的值不变.
例1? 下列等式的右边是怎样从左边得到的?
(1)
∵ ,
∴ .
(2)
为什么本题未给 ?
(2)
解: (1)
∵
∴
下列各组分式,能否由左边变形为右边?
(1) 与
反思: 运用分式的基本性质应注意什么?
①“都”
②“同一个”
③ “不为0”
(2) 与
(3) 与
(4)
不能
不能
能
能
(5)
不能
2ab-b2
例2:填空
(1)看分母如何变化,想分子如何变化;
(2)看分子如何变化,想分母如何变化;
你是怎么想的?
.
4n
x
a2+ab
填空
3x2-3xy
x+y
例2 不改变分式的值,使下列分式的分子和分母都不含“-”号:
分式符号变换的依据与分数符号变换
的依据相同,也遵循“同号得正,异号得负”的原则。
规律总结
1、不改变分式的值,把分子或分母中多项式的第一项都不含“-”号.
解:
拓展练习
1.若把分式
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
的 x 和 y 都扩大两倍,则分式的值( )
2.若把分式 中的 和 都扩大3倍,那么分式
的值( ).
A.扩大3倍 B.扩大9倍
C.扩大4倍 D.不变
B
A
分数的约分和通分在分数的运算中起着重要的作用,类似的,分式的约分和通分在分式的运算中也起着重要的作用。
与分数类似:根据分式的基本性质,也可以对分式进 行约分和通分.
注意
分析:分式的约分,即要求把分子与分母的公因式约去,为此,首先要找出分子与分母的公因式.
例题
约去系数的最大公约数,和分子分母相同字母的最低次幂
先把分子、分母分别分解因式,然后约去公因式.
约分:
在化简分式 时,小颖和小明的做法出现了分歧:
小颖:
小明:
你对他们俩的解法有何看法?说说看!
彻底约分后的分式叫最简分式.
一般约分要彻底, 使分子、分母没有公因式.
辨别对错
做一做
1、约分 :
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去相同字母的最低次幂;
注意:约分过程中,有时还需运用分式的符号法则使最后结果形式简捷;约分的依据是分式的基本性质。
规律总结:
(3)化简分式时通常要使结果成为最简分式或整式.
(2)若分子﹑分母含有多项式,则先将多项式
分解因式,然后约去分子﹑分母中所有的公因式;
约分的基本步骤:
观察与思考:
类比计算:
结论:
异分母的分式相加减,必须先通分。
化成同分母的分式。
通分的概念
根据分数的基本性质 , 异分母的分数可化为同分母的分数 , 这一过程叫做分数的通分 .
类似的,
根据分式的基本性质 , 异分母的分式可化为同分母的分式,这一过程叫做分式的通分 .
分式的通分:
把几个异分母的分式化成与原来的
分式相等的同分母的分式的变形,
叫做分式的通分。
议一议
(1)求分式
的最简公分母。
12
系数:各分母系数的最小公倍数。
因式:各分母所有因式的最高次幂。
三个分式的最简公分母为12x3y4z。
确定最简公分母的方法:
类型一、分母都是单项式时,
(1)定系数________________
(2)定字母_________
(3)定字母的次数_______
这样取出的因式的积,就是最简公分母
练一练
确定下列各组分式的最简公分母:
解:
最简公分母是
通分:
试确定下列分式的最简公分母:
最简公分母是:xy(x-y)2(x+y)
(分母中虽然有的因式是多项式,但仍然是积的形式。)
确定最简公分母的方法:
类型二、有多项式分母时:
先对多项式进行_______,把含 字母的因式看作一个整体,然后再执行:
(1)定系数________________
(2)定字母(或含字母的因式)______________________
(3)定字母(或含字母的因式)的次数_________
(2) 与
1.确定分式的最简公分母。
2.求商式(最简公分母除以各个分母,得 到的商式)
3.利用分式基本性质通分.
分式通分的步骤:
反思拓展
例题学习
把下列分式通分
尝试练习一:
通分
练习2
把下列分式通分
检测与练习:
A、12xyz B、12x3y4z C、24xyz D、24x3y4z
B
3、通分:
本节课学习了哪些内容?
1.什么是分式的基本性质?
分式的分子与分母乘(或除以)同一个不等于0的整式 ,分式的值不变.
2. 运用分式的基本性质应注意什么?
(1)分子、分母应同时做乘、除法中的同一种运算;
(2)所乘(或除以)的必须是同一个整式;
(3)所乘(或除以)的整式应该不等于零.
3、分式的约分 最简分式
4、分式的通分运算中, 它的意义是怎样的?通分运算的关键是什么?
把几个异分母的分式,分别化成与原来分式相等的同分母的分式,叫做分式的通分。 通分的关键是确定几个分式的公分母,
确定最简公分母的方法:
(1)将各个分式的分母分解因式;
(2)各分母系数的最小公倍数。
(3)各分母所含有的因式。
(4)各分母所含相同因式的最高次幂。
(5)所得的系数与各字母(或因式)的最高次幂的积(其中系数都取正数)
