人教版数学九年级上册第二十一章《21.2.4一元二次方程的根与系数的关系》课件(共24张PPT)
文档属性
| 名称 | 人教版数学九年级上册第二十一章《21.2.4一元二次方程的根与系数的关系》课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 19:53:44 | ||
图片预览






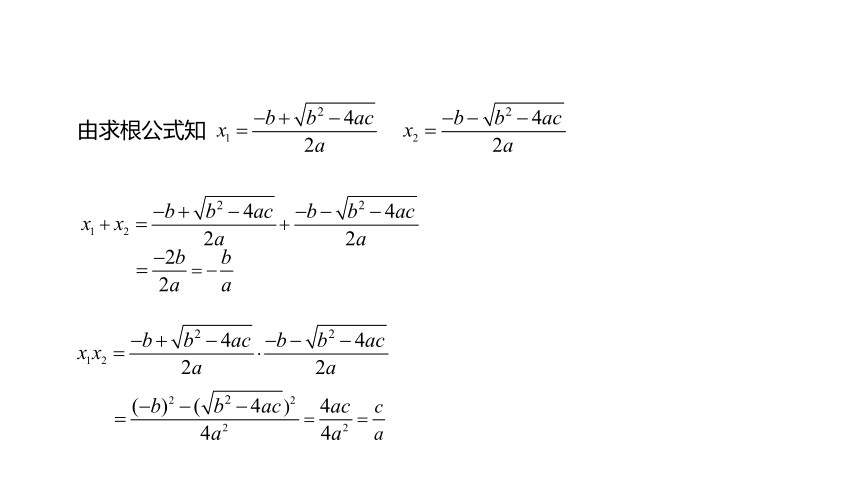


文档简介
第二十一章 二元一次方程
人教版数学九年级上册
21.2.4 一元二次方程的根与系数的关系
学习目标
1.了解一元二次方程的根与系数的关系。
2.能够应用一元二次方程根与系数关系解决简单的问题。
3.在探究一元二次方程根与系数的关系过程中感受由特殊到一般的认识过程。
一元二次方程的求根公式是由系数表达的,它反映了根与系数之间的一种运算关系,除此之外,同学们想知道一元二次方程两根的和、两根的积与系数之间又有怎样的关系吗?
导入新知
1.写出一元二次方程的一般式:
ax2+bx+c=0(a≠0)
3.如何用判别式 b2 - 4ac 来判断一元二次方程根的情况?
对一元二次方程: ax2 + bx +c = 0(a≠0).
b2 - 4ac > 0 时,方程有两个不相等的实数根.
b2 - 4ac = 0 时,方程有两个相等的实数根.
b2 - 4ac < 0 时,方程无实数根.
2.一元二次方程的求根公式:
回顾旧知
从因式分解法可知,方程 (x-x1)(x-x2)=0 (x1,x2为已知数) 的两根为x1和x2,将方程化为 x2+px+q=0 的形式,你能看出 x1,x2 与 p,q 之间的关系吗?
方程两个根的和、积与系数分别有如下关系:
x1+x2=-p,x1x2=q.
合作探究
一般的一元二次方程 ax2+bx+c=0 中,二次项系数 a 未必是1,它的两个根的和、积与系数又有怎样的关系呢?
由求根公式知
方程的两个根x1,x2和系数a,b,c有如下关系:
这表明任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
满足上述关系的前提条件
b2-4ac≥0.
根据一元二次方程的根与系数的关系,求下列方程两个根x1,x2的和与积:
(1) x2-6x-15=0; (2) 3x2+7x-9=0; (3) 5x-1=4x2.
解: (1)x1+x2=-(-6)=6,x1x2=-15.
(3)方程化为4x2-5x+1=0,
典型例题
与一元二次方程 ax2+bx+c=0(a≠0) 的两个根 x1,x2 有关的几个代数式的变形:
合作探究
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和、两根之积的形式,再整体代入.
?
?
?
A
典型例题
?
?
求解此类问题时,必须将求出的字母值代回原方程进行检验,看是否满足判别式Δ>0 ,否则可能会多解.
解:根据题意,得 x1+x2=-3,x1x2=-1,
所以 x1-1+x2-1=-5, (x1-1)(x2-1)=x1x2- (x1+x2)+1=-1+3+1=3,
所以以 x1-1 和 x2-1 为根的一个一元二次方程可以是 x2+5x+3=0(答案不唯一).
3.已知 x1,x2 是方程 x2+3x-1=0 的两个根,求以x1-1和x2-1为根的一元二次方程.
1.不解方程,求下列方程两个根的和与积.
(1)x2-3x=15; (2) 3x2+2=1-4x;
(3) 5x2-1=4x2+x; (4) 2x2-x+2=3x+1.
解:(1)方程化为 x2-3x-15=0,
x1+x2=-(-3)=3,x1x2=-15.
?
课堂练习
?
2.不解方程,求下列方程两个根的和与积.
(1)x2-3x=15; (2) 3x2+2=1-4x;
(3) 5x2-1=4x2+x; (4) 2x2-x+2=3x+1.
?
0
解:根据题意得 α+β=3,αβ=-4,
所以原式 = α(α+β)-3α
=3α-3α
=0.
4.已知关于 x 的一元二次方程 x2-6x+q=0 有一个根为 2,求方程的另一根和 q 的值.
解:设方程的另一个根为 a,则 2+a=-(-6)=6,
解得 a=4,
则 q=2×4=8.
1.关于 x 的一元二次方程 x2-(a2-2a)x+a-1=0 的两个实数根互为相反数,
则 a 的值为( )
B
A.2 B.0 C.1 D.2或0
解:∵方程 x2-(a2-2a)x+a-1=0 的两个实数根互为相反数,
∴a2-2a=0,解得a=0或a=2,
当a=2时,方程为x2+1=0,该方程无实数根,舍去;
当a=0时,方程为x2-1=0,该方程有两个不相等的实数根.
∴a=0.故选B.
中考实题
2.已知x1,x2是一元二次方程 x2?2x=0 的两个实数根,下列结论错误的是( )
D
?
解:?=(?2)?? 4×1×0=4>0,∴x1≠x2,选项A正确;
∵x1是一元二次方程x?-2x=0的实数根,
∴ x12 ?2x1 =0,选项B正确;
∵x1,x2是一元二次方程x2?2x=0的两个实数根,
∴ x1+x2=2 ,x1 x2 =0,选项C正确,选项D错误.
?
?
?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}一元二次方程 ax2+bx+c=0(a≠0) 的根与系数的关系
数学语言
文字语言
一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
使用条件
1.方程是一元二次方程,即二次项系数不为 0;
2.方程有实数根,即 Δ≥0.
重要结论
1.若一元二次方程 x2+px+q=0 的两根为 x1,x2,则 x1+x2=-p,x1x2=q.
2.以实数 x1,x2 为两根的二次项系数为1的一元二次方程是
x2-(x1+x2)x+x1x2=0.
归纳总结
再 见
人教版数学九年级上册
21.2.4 一元二次方程的根与系数的关系
学习目标
1.了解一元二次方程的根与系数的关系。
2.能够应用一元二次方程根与系数关系解决简单的问题。
3.在探究一元二次方程根与系数的关系过程中感受由特殊到一般的认识过程。
一元二次方程的求根公式是由系数表达的,它反映了根与系数之间的一种运算关系,除此之外,同学们想知道一元二次方程两根的和、两根的积与系数之间又有怎样的关系吗?
导入新知
1.写出一元二次方程的一般式:
ax2+bx+c=0(a≠0)
3.如何用判别式 b2 - 4ac 来判断一元二次方程根的情况?
对一元二次方程: ax2 + bx +c = 0(a≠0).
b2 - 4ac > 0 时,方程有两个不相等的实数根.
b2 - 4ac = 0 时,方程有两个相等的实数根.
b2 - 4ac < 0 时,方程无实数根.
2.一元二次方程的求根公式:
回顾旧知
从因式分解法可知,方程 (x-x1)(x-x2)=0 (x1,x2为已知数) 的两根为x1和x2,将方程化为 x2+px+q=0 的形式,你能看出 x1,x2 与 p,q 之间的关系吗?
方程两个根的和、积与系数分别有如下关系:
x1+x2=-p,x1x2=q.
合作探究
一般的一元二次方程 ax2+bx+c=0 中,二次项系数 a 未必是1,它的两个根的和、积与系数又有怎样的关系呢?
由求根公式知
方程的两个根x1,x2和系数a,b,c有如下关系:
这表明任何一个一元二次方程的根与系数的关系为:
两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
满足上述关系的前提条件
b2-4ac≥0.
根据一元二次方程的根与系数的关系,求下列方程两个根x1,x2的和与积:
(1) x2-6x-15=0; (2) 3x2+7x-9=0; (3) 5x-1=4x2.
解: (1)x1+x2=-(-6)=6,x1x2=-15.
(3)方程化为4x2-5x+1=0,
典型例题
与一元二次方程 ax2+bx+c=0(a≠0) 的两个根 x1,x2 有关的几个代数式的变形:
合作探究
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和、两根之积的形式,再整体代入.
?
?
?
A
典型例题
?
?
求解此类问题时,必须将求出的字母值代回原方程进行检验,看是否满足判别式Δ>0 ,否则可能会多解.
解:根据题意,得 x1+x2=-3,x1x2=-1,
所以 x1-1+x2-1=-5, (x1-1)(x2-1)=x1x2- (x1+x2)+1=-1+3+1=3,
所以以 x1-1 和 x2-1 为根的一个一元二次方程可以是 x2+5x+3=0(答案不唯一).
3.已知 x1,x2 是方程 x2+3x-1=0 的两个根,求以x1-1和x2-1为根的一元二次方程.
1.不解方程,求下列方程两个根的和与积.
(1)x2-3x=15; (2) 3x2+2=1-4x;
(3) 5x2-1=4x2+x; (4) 2x2-x+2=3x+1.
解:(1)方程化为 x2-3x-15=0,
x1+x2=-(-3)=3,x1x2=-15.
?
课堂练习
?
2.不解方程,求下列方程两个根的和与积.
(1)x2-3x=15; (2) 3x2+2=1-4x;
(3) 5x2-1=4x2+x; (4) 2x2-x+2=3x+1.
?
0
解:根据题意得 α+β=3,αβ=-4,
所以原式 = α(α+β)-3α
=3α-3α
=0.
4.已知关于 x 的一元二次方程 x2-6x+q=0 有一个根为 2,求方程的另一根和 q 的值.
解:设方程的另一个根为 a,则 2+a=-(-6)=6,
解得 a=4,
则 q=2×4=8.
1.关于 x 的一元二次方程 x2-(a2-2a)x+a-1=0 的两个实数根互为相反数,
则 a 的值为( )
B
A.2 B.0 C.1 D.2或0
解:∵方程 x2-(a2-2a)x+a-1=0 的两个实数根互为相反数,
∴a2-2a=0,解得a=0或a=2,
当a=2时,方程为x2+1=0,该方程无实数根,舍去;
当a=0时,方程为x2-1=0,该方程有两个不相等的实数根.
∴a=0.故选B.
中考实题
2.已知x1,x2是一元二次方程 x2?2x=0 的两个实数根,下列结论错误的是( )
D
?
解:?=(?2)?? 4×1×0=4>0,∴x1≠x2,选项A正确;
∵x1是一元二次方程x?-2x=0的实数根,
∴ x12 ?2x1 =0,选项B正确;
∵x1,x2是一元二次方程x2?2x=0的两个实数根,
∴ x1+x2=2 ,x1 x2 =0,选项C正确,选项D错误.
?
?
?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}一元二次方程 ax2+bx+c=0(a≠0) 的根与系数的关系
数学语言
文字语言
一元二次方程的两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比.
使用条件
1.方程是一元二次方程,即二次项系数不为 0;
2.方程有实数根,即 Δ≥0.
重要结论
1.若一元二次方程 x2+px+q=0 的两根为 x1,x2,则 x1+x2=-p,x1x2=q.
2.以实数 x1,x2 为两根的二次项系数为1的一元二次方程是
x2-(x1+x2)x+x1x2=0.
归纳总结
再 见
同课章节目录
