人教版数学九年级下册27.1 图形的相似(第二课时)课件(共21张ppt)
文档属性
| 名称 | 人教版数学九年级下册27.1 图形的相似(第二课时)课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 216.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览






文档简介
第二十七章
图形的相似(第二课时)
问题:上节课我们介绍了什么样的图形是相似图形?
本节课我们将介绍两个相似图形都有哪些主要特征.
一.查学诊断
A
B
C
A1
B1
C1
正三角形
缩小
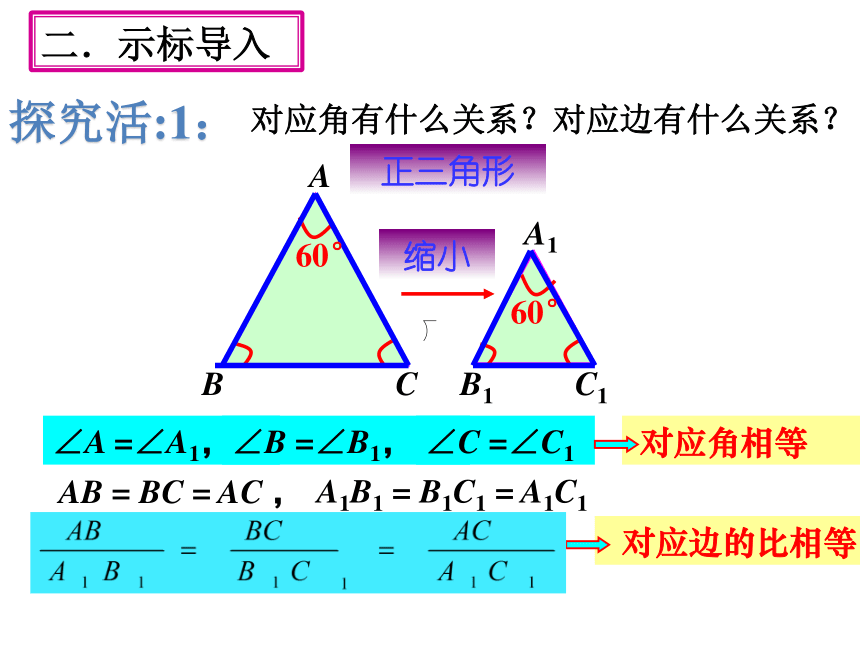
对应角有什么关系?对应边有什么关系?
∠A =∠A1,
∠B =∠B1,
∠C =∠C1
AB = BC = AC ,
A1B1 = B1C1 = A1C1
60°
60°
对应角相等
对应边的比相等
探究活:1:
二.示标导入
正六边形
放大
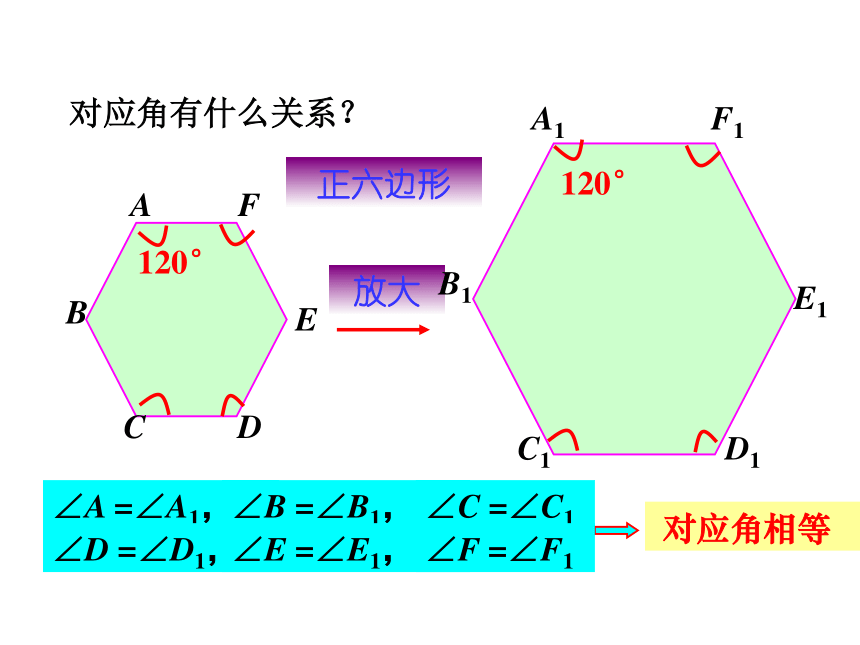
对应角有什么关系?
120°
120°
∠A =∠A1,
∠B =∠B1,
∠C =∠C1
对应角相等
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
∠D =∠D1,
∠E =∠E1,
∠F =∠F1
正六边形
放大
对应边有什么关系?
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
AB = BC = CD = DE = EF = FA ,
A1B1 = B1C1 = C1D1 = D1E1 = E1F1 = F1A1
对应边的比相等
A1B1
AB
B1C1
BC
=
C1D1
CD
D1E1
DE
=
E1F1
EF
F1A1
FA
=
=
=
相似正多边形各对应角相等、各对应边的比相等.
这个结论对于一般的相似多边形是否成立呢?
结论:
结论:
(1)相似多边形的特征:相似多边形的对应角______,对应边的比_______.
反之,如果两个多边形的对应角______,对应边的比_______,那么这两个多边形_______.
相等
相等
相等
相等
相似
(2)相似比:相似多边形________的比
称为相似比.
相似比为1时,相似的两个图形
______,
因此________形是一种特殊的相似形.
对应边
全等
全等
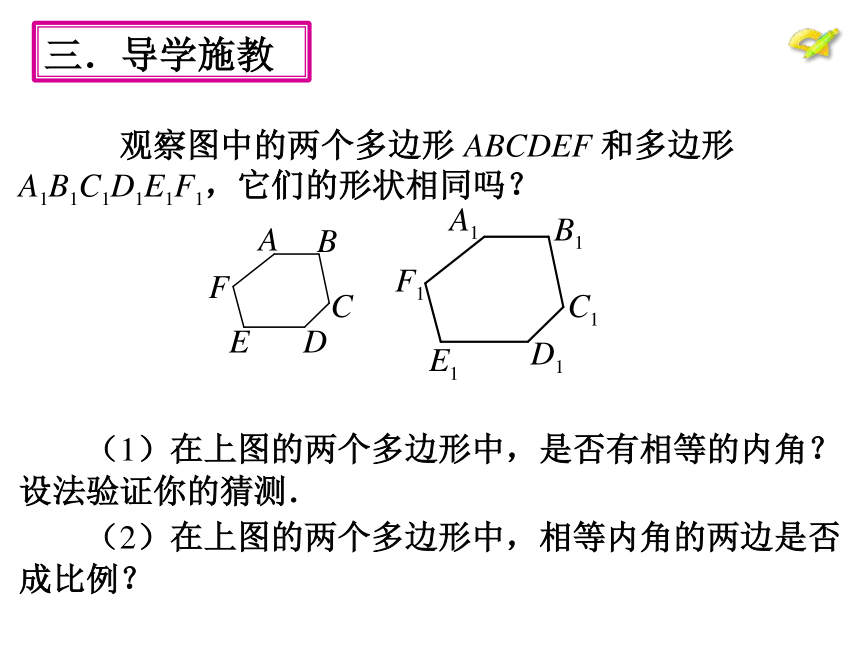
观察图中的两个多边形 ABCDEF 和多边形 A1B1C1D1E1F1,它们的形状相同吗?
(1)在上图的两个多边形中,是否有相等的内角?设法验证你的猜测.
(2)在上图的两个多边形中,相等内角的两边是否成比例?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
三.导学施教
(1)从上面的测量结果来看,大家能否猜测出相似多边形的定义呢?
(2)是形状相同的多边形都有这种关系呢,还是只有六边形才有呢?
两个边数相同的多边形,如果它们的对应角分别相等;对应边成比例,那么这两个多边形叫做相似多边形。
两个多边形相似的条件(两个)
相似多边形的性质:
相似多边形对应角相等,对应边成比例。
(对应边的比相等).
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.
相似多边形的判定方法:
例1: 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
相似多边形性质的运用:
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
1、如果两个多边形仅有对应角相等,
它们相似吗?如果仅有对应边相等呢?
若不相似,请举出反例。
四.练测促学
判断两个多边形是否相似
解: ∵ 正方形,菱形的四条边都相等.
∴ 它们的对应边成比例,k = 3 : 4.
∵ 正方形的四个内角均为直角,而菱形的内角有钝角有锐角.
∴ 它们的对应角不相等.
∴ 这一组图形不相似.
判断两个多边形是否相似
解:∵ 正方形和矩形的四个内角都是直角.
∴ 它们的对应角相等.
∵ 对应边 3 : 6 ≠ 3 : 8.
∴ 它们的对应边不成比例.
∴ 这一组图形不相似.
2.我是长3m,宽1.5m的矩形黑板.镶在我外围的木质边框宽10cm ,边框的内外边缘所成的矩形相似吗?为什么?
它们不相似,因为对应边的比不相等.
长3米
宽1.5米
有的时候,直觉是不可靠的.
1、如图,两个等边三角形、两个矩形、两个正方形、两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
五.拓展延伸
B
2. 如图所示的两个五边形相似,求未知边a、b、
c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示: 可知两图形的相似比为:
∴
b = 4.5
a = 3
c = 4
d = 6
课堂小结
(1)本节课我们都学习了哪些内容?
1、相似多边形的定义
2、相似比的定义:
3、相似多边形的性质:
4、相似多边形的判定:
5、比例线段:
(2)在学习的过程中,你有怎样的收获?
(1)课本第27页,3、4题;
(2)阅读课本29-31页
六.布置作业
图形的相似(第二课时)
问题:上节课我们介绍了什么样的图形是相似图形?
本节课我们将介绍两个相似图形都有哪些主要特征.
一.查学诊断
A
B
C
A1
B1
C1
正三角形
缩小
对应角有什么关系?对应边有什么关系?
∠A =∠A1,
∠B =∠B1,
∠C =∠C1
AB = BC = AC ,
A1B1 = B1C1 = A1C1
60°
60°
对应角相等
对应边的比相等
探究活:1:
二.示标导入
正六边形
放大
对应角有什么关系?
120°
120°
∠A =∠A1,
∠B =∠B1,
∠C =∠C1
对应角相等
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
∠D =∠D1,
∠E =∠E1,
∠F =∠F1
正六边形
放大
对应边有什么关系?
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
AB = BC = CD = DE = EF = FA ,
A1B1 = B1C1 = C1D1 = D1E1 = E1F1 = F1A1
对应边的比相等
A1B1
AB
B1C1
BC
=
C1D1
CD
D1E1
DE
=
E1F1
EF
F1A1
FA
=
=
=
相似正多边形各对应角相等、各对应边的比相等.
这个结论对于一般的相似多边形是否成立呢?
结论:
结论:
(1)相似多边形的特征:相似多边形的对应角______,对应边的比_______.
反之,如果两个多边形的对应角______,对应边的比_______,那么这两个多边形_______.
相等
相等
相等
相等
相似
(2)相似比:相似多边形________的比
称为相似比.
相似比为1时,相似的两个图形
______,
因此________形是一种特殊的相似形.
对应边
全等
全等
观察图中的两个多边形 ABCDEF 和多边形 A1B1C1D1E1F1,它们的形状相同吗?
(1)在上图的两个多边形中,是否有相等的内角?设法验证你的猜测.
(2)在上图的两个多边形中,相等内角的两边是否成比例?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
三.导学施教
(1)从上面的测量结果来看,大家能否猜测出相似多边形的定义呢?
(2)是形状相同的多边形都有这种关系呢,还是只有六边形才有呢?
两个边数相同的多边形,如果它们的对应角分别相等;对应边成比例,那么这两个多边形叫做相似多边形。
两个多边形相似的条件(两个)
相似多边形的性质:
相似多边形对应角相等,对应边成比例。
(对应边的比相等).
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.
相似多边形的判定方法:
例1: 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
相似多边形性质的运用:
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
1、如果两个多边形仅有对应角相等,
它们相似吗?如果仅有对应边相等呢?
若不相似,请举出反例。
四.练测促学
判断两个多边形是否相似
解: ∵ 正方形,菱形的四条边都相等.
∴ 它们的对应边成比例,k = 3 : 4.
∵ 正方形的四个内角均为直角,而菱形的内角有钝角有锐角.
∴ 它们的对应角不相等.
∴ 这一组图形不相似.
判断两个多边形是否相似
解:∵ 正方形和矩形的四个内角都是直角.
∴ 它们的对应角相等.
∵ 对应边 3 : 6 ≠ 3 : 8.
∴ 它们的对应边不成比例.
∴ 这一组图形不相似.
2.我是长3m,宽1.5m的矩形黑板.镶在我外围的木质边框宽10cm ,边框的内外边缘所成的矩形相似吗?为什么?
它们不相似,因为对应边的比不相等.
长3米
宽1.5米
有的时候,直觉是不可靠的.
1、如图,两个等边三角形、两个矩形、两个正方形、两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
五.拓展延伸
B
2. 如图所示的两个五边形相似,求未知边a、b、
c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示: 可知两图形的相似比为:
∴
b = 4.5
a = 3
c = 4
d = 6
课堂小结
(1)本节课我们都学习了哪些内容?
1、相似多边形的定义
2、相似比的定义:
3、相似多边形的性质:
4、相似多边形的判定:
5、比例线段:
(2)在学习的过程中,你有怎样的收获?
(1)课本第27页,3、4题;
(2)阅读课本29-31页
六.布置作业
