27.2.1 三边法、两边及其夹角法 课件
文档属性
| 名称 | 27.2.1 三边法、两边及其夹角法 课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 847.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 20:22:18 | ||
图片预览

文档简介
第二十七章 相 似
27.2.1 相似三角形的判定(2)
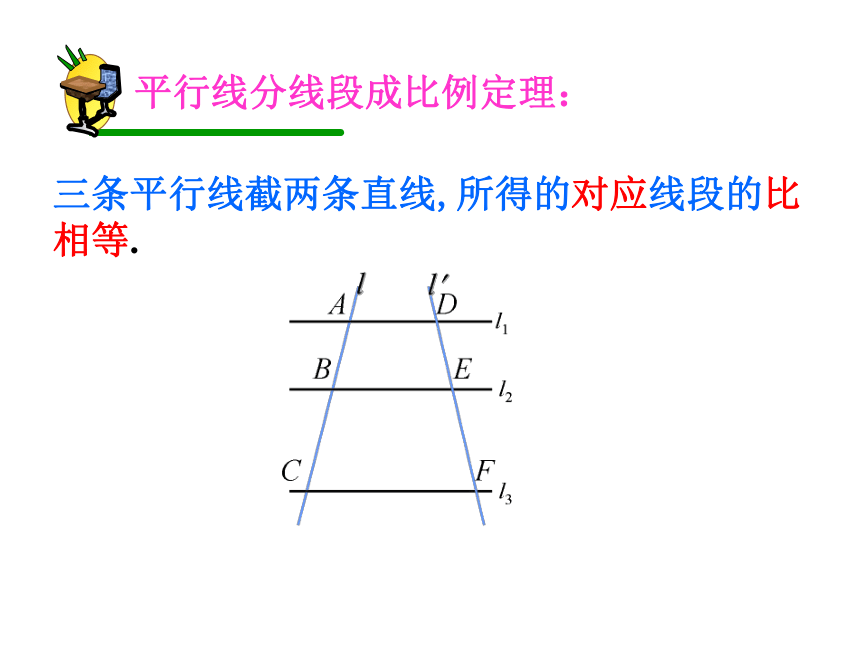
三条平行线截两条直线,所得的对应线段的比相等.
平行线分线段成比例定理:
l2
l3
l1
l3
l
l?
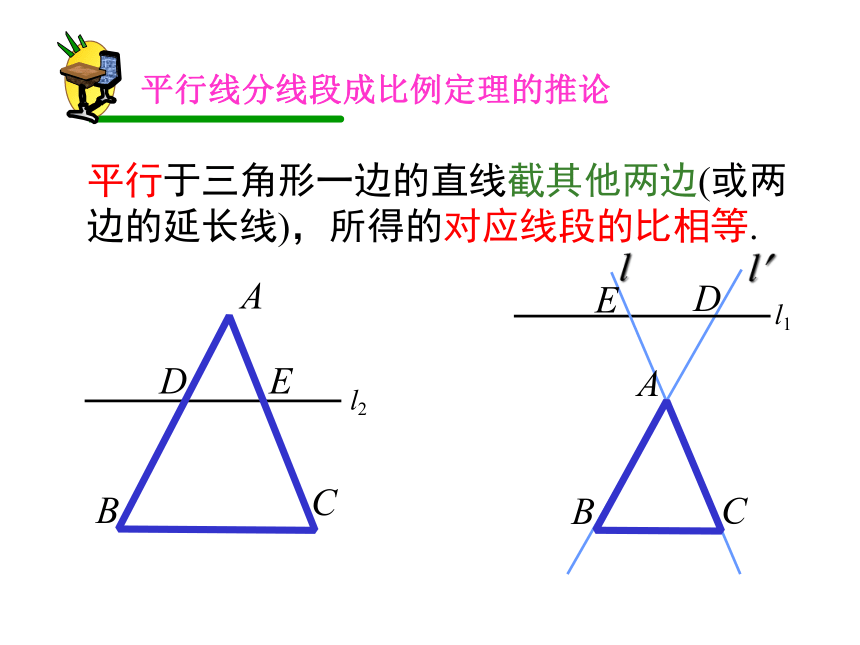
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
平行线分线段成比例定理的推论
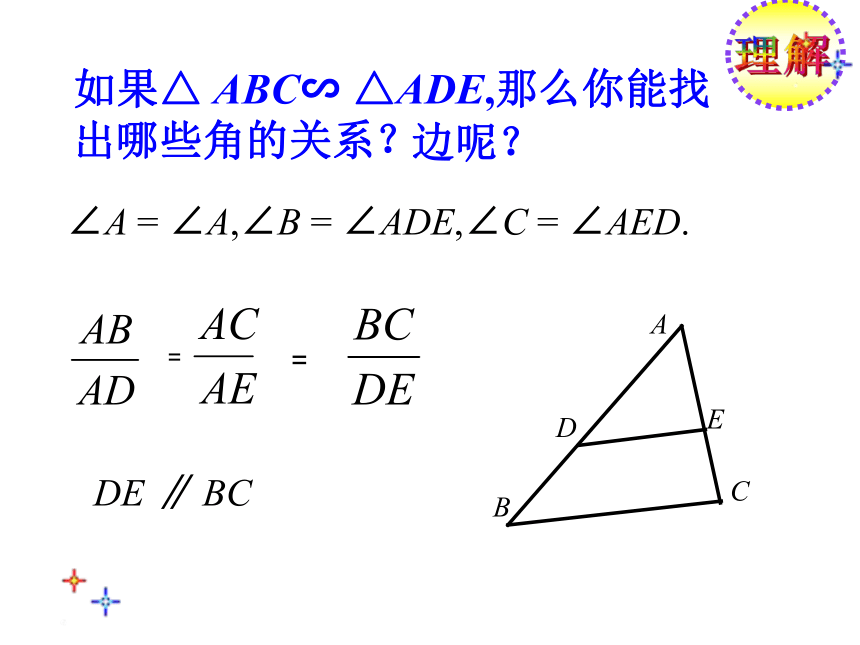
如果△ ABC∽ △ADE,那么你能找出哪些角的关系?
∠A = ∠A,∠B = ∠ADE,∠C = ∠AED.
边呢?
A
D
E
B
C
=
=
DE ∥ BC
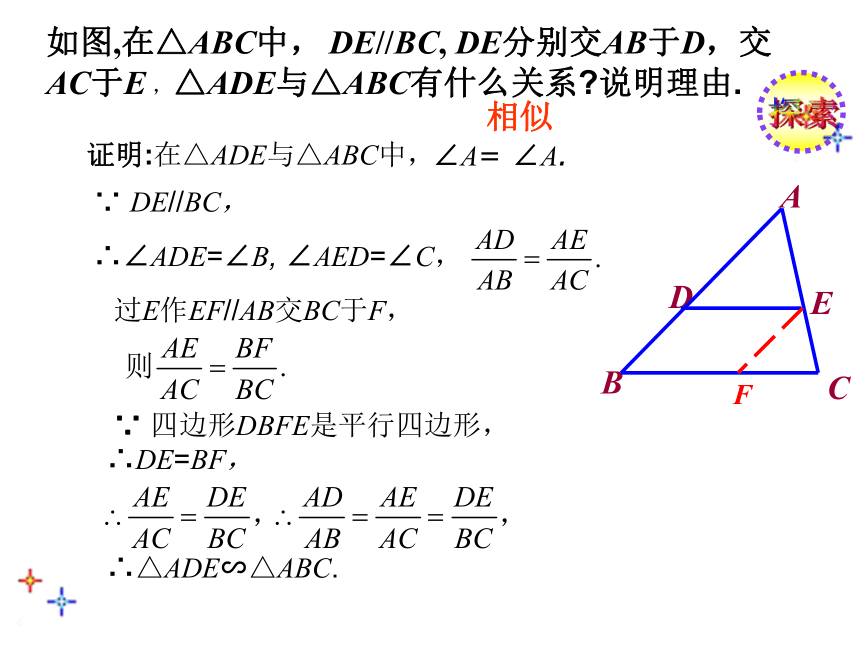
如图,在△ABC中, DE//BC, DE分别交AB于D,交AC于E ,△ADE与△ABC有什么关系?说明理由.
相似
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A= ∠A.
∵ DE//BC,
∴∠ADE=∠B, ∠AED=∠C,
过E作EF//AB交BC于F,
∵ 四边形DBFE是平行四边形,
F
∴DE=BF,
∴△ADE∽△ABC.
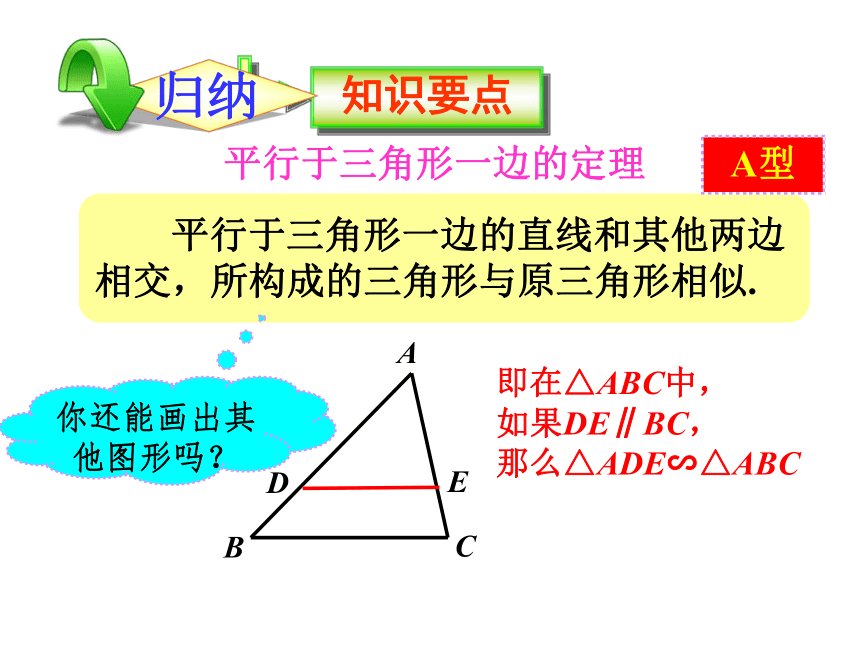
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
知识要点
平行于三角形一边的定理
A
B
C
D
E
即在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC
A型
你还能画出其他图形吗?
归纳
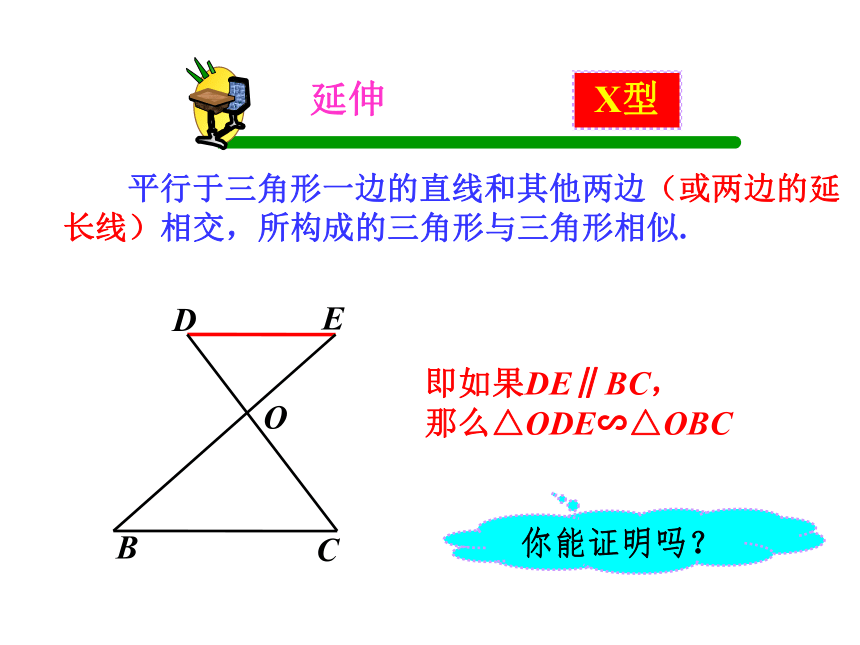
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似.
D
E
O
C
B
延伸
即如果DE∥BC,
那么△ODE∽△OBC
你能证明吗?
X型
平行于三角形一边的直线与其他两边(或延长线)相交,所得的三角形与原三角形________.
相似
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
思考:有没有其他简单的办法判断两个三角形相似?
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.
探究2
是否有△ABC∽△A′B′C′?
A
B
C
C′
B′
A′
三边对应成 比例
求证: △ .
∽△
A
B
C
D
E
∴
又
∴
同理
∴
∴
∥
∽
∽
∴
∽
∽
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
知识要点
判定三角形相似的定理之一
△ABC∽△A′B′C′.
即:
如果
那么
A′
B′
C′
A
B
C
三边对应成比例,两三角形相似.
边边边
S
S
S
√
归纳
例题讲解:
根据下列条件,判断 与 是否相似
AB=4CM ,BC=6CM , AC=8CM.
A/B/=12CM ,B/C/=18CM, A/C/=21CM
解
. 与 的三组对应边的边不等,它们不相似
:
练习册P137页第4 . 5题
P138页10题及中考真题
相似三角形的判定方法有几种?
1.定义判定法
3.边边边判定法
2.平行判定法
比较复杂,烦琐
只能在特定的图形里面使用
小结
27.2.1 相似三角形的判定(2)
三条平行线截两条直线,所得的对应线段的比相等.
平行线分线段成比例定理:
l2
l3
l1
l3
l
l?
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段的比相等.
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
平行线分线段成比例定理的推论
如果△ ABC∽ △ADE,那么你能找出哪些角的关系?
∠A = ∠A,∠B = ∠ADE,∠C = ∠AED.
边呢?
A
D
E
B
C
=
=
DE ∥ BC
如图,在△ABC中, DE//BC, DE分别交AB于D,交AC于E ,△ADE与△ABC有什么关系?说明理由.
相似
A
B
C
D
E
证明:在△ADE与△ABC中,
∠A= ∠A.
∵ DE//BC,
∴∠ADE=∠B, ∠AED=∠C,
过E作EF//AB交BC于F,
∵ 四边形DBFE是平行四边形,
F
∴DE=BF,
∴△ADE∽△ABC.
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
知识要点
平行于三角形一边的定理
A
B
C
D
E
即在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC
A型
你还能画出其他图形吗?
归纳
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与三角形相似.
D
E
O
C
B
延伸
即如果DE∥BC,
那么△ODE∽△OBC
你能证明吗?
X型
平行于三角形一边的直线与其他两边(或延长线)相交,所得的三角形与原三角形________.
相似
“A”型
“X”型
(图2)
D
E
O
B
C
A
B
C
D
E
(图1)
思考:有没有其他简单的办法判断两个三角形相似?
任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同桌交流一下,看看是否有同样的结论.
探究2
是否有△ABC∽△A′B′C′?
A
B
C
C′
B′
A′
三边对应成 比例
求证: △ .
∽△
A
B
C
D
E
∴
又
∴
同理
∴
∴
∥
∽
∽
∴
∽
∽
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
知识要点
判定三角形相似的定理之一
△ABC∽△A′B′C′.
即:
如果
那么
A′
B′
C′
A
B
C
三边对应成比例,两三角形相似.
边边边
S
S
S
√
归纳
例题讲解:
根据下列条件,判断 与 是否相似
AB=4CM ,BC=6CM , AC=8CM.
A/B/=12CM ,B/C/=18CM, A/C/=21CM
解
. 与 的三组对应边的边不等,它们不相似
:
练习册P137页第4 . 5题
P138页10题及中考真题
相似三角形的判定方法有几种?
1.定义判定法
3.边边边判定法
2.平行判定法
比较复杂,烦琐
只能在特定的图形里面使用
小结
