人教版数学九年级下册27.2.2相似三角形的性质课件(共14张ppt)
文档属性
| 名称 | 人教版数学九年级下册27.2.2相似三角形的性质课件(共14张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 19:30:37 | ||
图片预览





文档简介
27.2.2 相似三角形的性质
1.识别两个三角形相似的简便方法有哪些?
2.在△ABC与△A/B/C/中,AB=10cm,AC=6cm,BC=8cm,A/B/=5cm,A/C/=3cm,B/C/=4cm,这两个三角形相似吗?说明理由.如果相似,它们的相似比是多少?
回顾与思考
相似的两个三角形
它们的对应角相等
对应边会成比例
对应高的比
对应中线的比
对应角平分线的比
相似三角形
都等于相似比
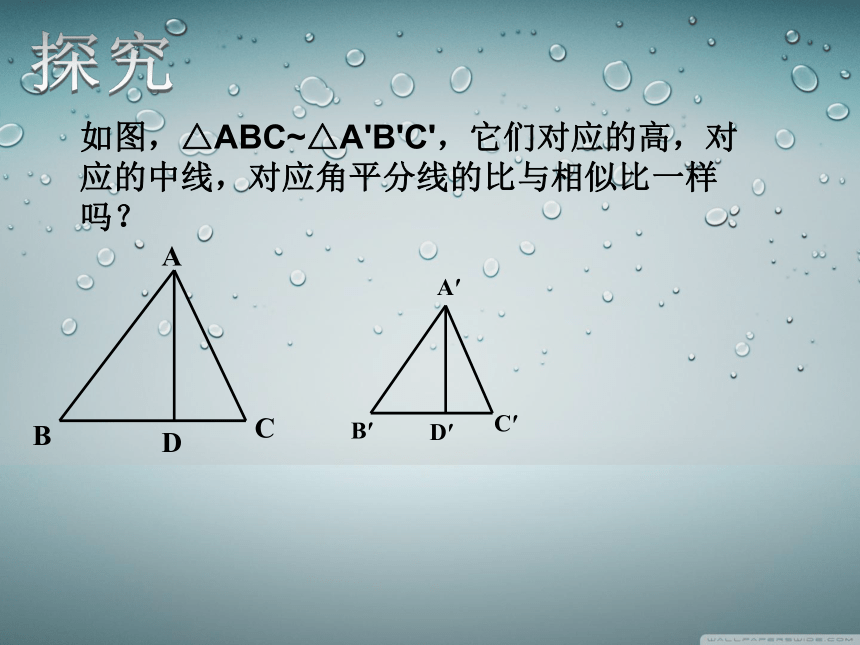
如图,△ABC~△A'B'C',它们对应的高,对应的中线,对应角平分线的比与相似比一样吗?
A
B
C
D
A′
B′
C′
D′
A′
B′
C′
D′
A
B
C
D
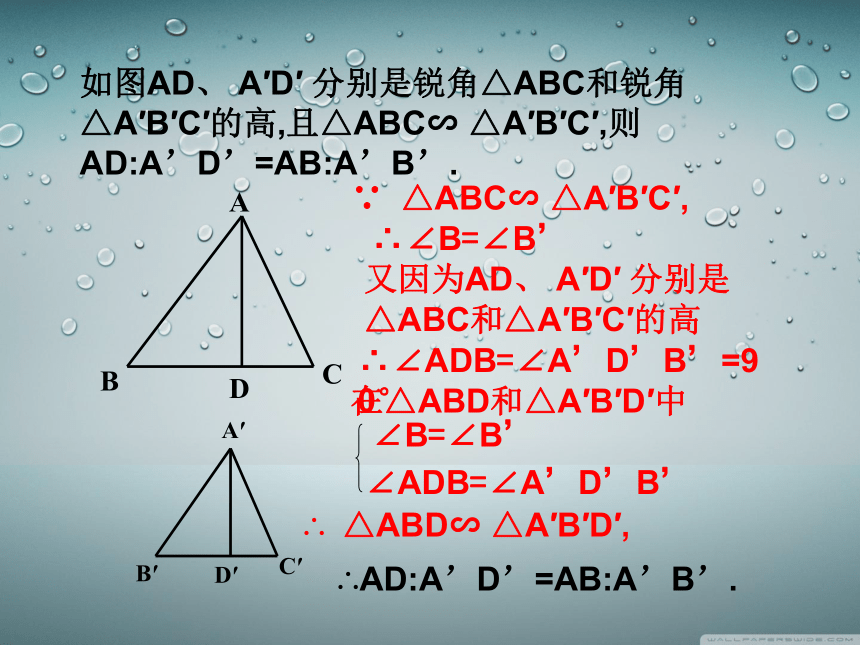
如图AD、 A′D′ 分别是锐角△ABC和锐角△A′B′C′的高,且△ABC∽ △A′B′C′,则AD:A’D’=AB:A’B’.
∵ △ABC∽ △A′B′C′,
∴∠B=∠B’
又因为AD、 A′D′ 分别是△ABC和△A′B′C′的高
∴∠ADB=∠A’D’B’=90°
在△ABD和△A′B′D′中
∠B=∠B’
∠ADB=∠A’D’B’
∴ △ABD∽ △A′B′D′,
∴AD:A’D’=AB:A’B’.
填空:
(1)两个三角形的对应边的比为3:4,则这两个三角形的对应角平分线的比为__3:4___ ,对应边上的高的比为_3:4___,对应边上的中线的比为__3:4__
(2)相似三角形对应角平分线比为0.2,则相似比为___0.2___,对应中线的比等于__0.2___;
相似三角形对应高的比,对应中线的比、对应角平分线的比都等于相似比.
相似三角形周长的比等于相似比.
如果△ABC∽△A′B′C′,且△ABC与△A′B′C′
的相似比为k,即 ,那么
相似三角形面积的比等于相似比的平方。
A
B
C
A’
B’
C’
△ABC~△A’B’C’,相似比为K
D
D’
S BC · AD
S’ B’C’·A’D’
=
1/2 ·
1/2 ·
=
BC · AD
B’C’ · A’D’
K
K
=
K
2
A
B
C
D
E
F
相似三角形的性质
对应角相等
对应边成比例
对应高的比,对应中线的比、对应角平分线的比都等于相似比.
相似比等于对应边的比
周长的比等于相似比
面积的比等于相似比的平方
1、两个相似多边形的面积比为4:1,则它们的相似比为_______,周长比为_______。
2、如果把一个三角形的三条边长都扩大为原来
的100倍,则面积扩大为原来的_______倍,周长
扩大为______倍。
2:1
2:1
10000
100
10
10
3、如果把一个三角形的面积扩大为原来的100倍,则边长为原来的_____倍,周长为原来的______倍。
判断题(正确的打“√”,错误的画“×”)
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍
( √ )
( × )
1.识别两个三角形相似的简便方法有哪些?
2.在△ABC与△A/B/C/中,AB=10cm,AC=6cm,BC=8cm,A/B/=5cm,A/C/=3cm,B/C/=4cm,这两个三角形相似吗?说明理由.如果相似,它们的相似比是多少?
回顾与思考
相似的两个三角形
它们的对应角相等
对应边会成比例
对应高的比
对应中线的比
对应角平分线的比
相似三角形
都等于相似比
如图,△ABC~△A'B'C',它们对应的高,对应的中线,对应角平分线的比与相似比一样吗?
A
B
C
D
A′
B′
C′
D′
A′
B′
C′
D′
A
B
C
D
如图AD、 A′D′ 分别是锐角△ABC和锐角△A′B′C′的高,且△ABC∽ △A′B′C′,则AD:A’D’=AB:A’B’.
∵ △ABC∽ △A′B′C′,
∴∠B=∠B’
又因为AD、 A′D′ 分别是△ABC和△A′B′C′的高
∴∠ADB=∠A’D’B’=90°
在△ABD和△A′B′D′中
∠B=∠B’
∠ADB=∠A’D’B’
∴ △ABD∽ △A′B′D′,
∴AD:A’D’=AB:A’B’.
填空:
(1)两个三角形的对应边的比为3:4,则这两个三角形的对应角平分线的比为__3:4___ ,对应边上的高的比为_3:4___,对应边上的中线的比为__3:4__
(2)相似三角形对应角平分线比为0.2,则相似比为___0.2___,对应中线的比等于__0.2___;
相似三角形对应高的比,对应中线的比、对应角平分线的比都等于相似比.
相似三角形周长的比等于相似比.
如果△ABC∽△A′B′C′,且△ABC与△A′B′C′
的相似比为k,即 ,那么
相似三角形面积的比等于相似比的平方。
A
B
C
A’
B’
C’
△ABC~△A’B’C’,相似比为K
D
D’
S BC · AD
S’ B’C’·A’D’
=
1/2 ·
1/2 ·
=
BC · AD
B’C’ · A’D’
K
K
=
K
2
A
B
C
D
E
F
相似三角形的性质
对应角相等
对应边成比例
对应高的比,对应中线的比、对应角平分线的比都等于相似比.
相似比等于对应边的比
周长的比等于相似比
面积的比等于相似比的平方
1、两个相似多边形的面积比为4:1,则它们的相似比为_______,周长比为_______。
2、如果把一个三角形的三条边长都扩大为原来
的100倍,则面积扩大为原来的_______倍,周长
扩大为______倍。
2:1
2:1
10000
100
10
10
3、如果把一个三角形的面积扩大为原来的100倍,则边长为原来的_____倍,周长为原来的______倍。
判断题(正确的打“√”,错误的画“×”)
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍
( √ )
( × )
