人教版数学九年级下册27.2.3视线遮挡问题课件(共21张ppt)
文档属性
| 名称 | 人教版数学九年级下册27.2.3视线遮挡问题课件(共21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 19:54:26 | ||
图片预览





文档简介
(1)同学们玩过“捉迷藏”的游戏吗?你认为躲藏者藏在何处,才不容易被寻找者发现?
(2)如图1,小强站在楼下能看到3楼窗口内的小明吗?为什么?
(3)你认为小强站在什么位置时,才能看到小明?
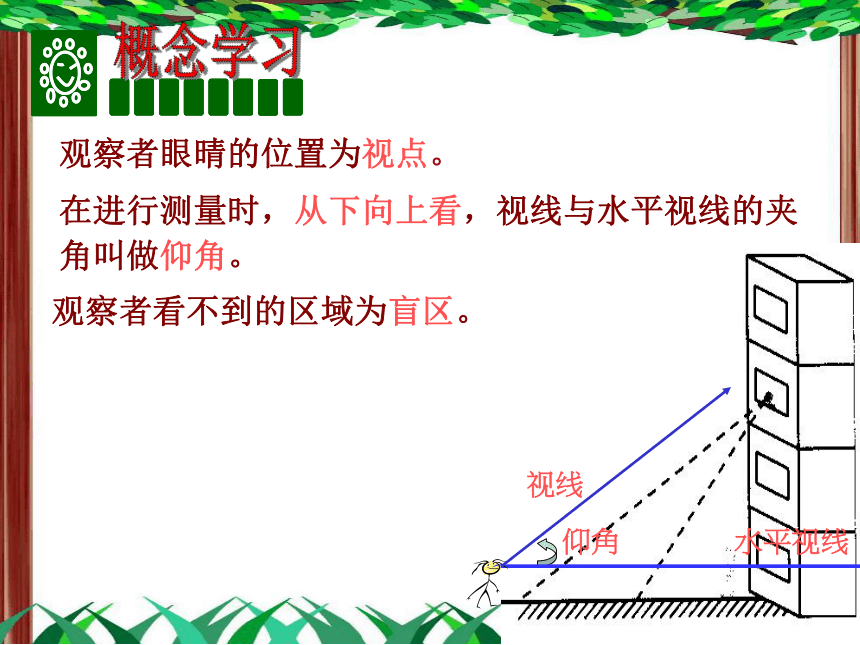
在进行测量时,从下向上看,视线与水平视线的夹角叫做仰角。
水平视线
视线
观察者眼晴的位置为视点。
观察者看不到的区域为盲区。
仰角
王鹏为了测量校园内一棵大树的高度,他在大树前处竖了一根标杆CD(如图所示),然后他往后退,当他退至B处,看到标杆顶端C恰好挡住了大树顶端E时,三点在同一条直线上。你认为他这样做能测出树高吗?如果可以,请说明理由;如果不可以,请说明为什么?
E
F
C
D
A
B
G
H
A
H
E
C
G
EF =FH + EH = AB+EH
即: 大树高
∵ △ACG∽△AEH
∴ =
A G CG
AH EH
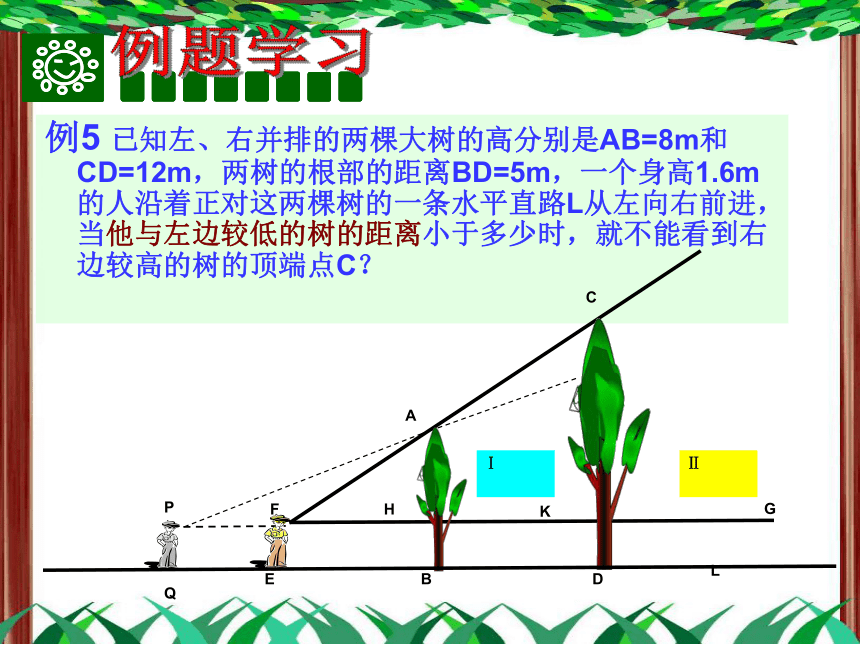
例5 已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m,一个身高1.6m的人沿着正对这两棵树的一条水平直路L从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?
D
B
G
F
C
A
E
H
P
Q
K
Ⅰ
Ⅱ
L
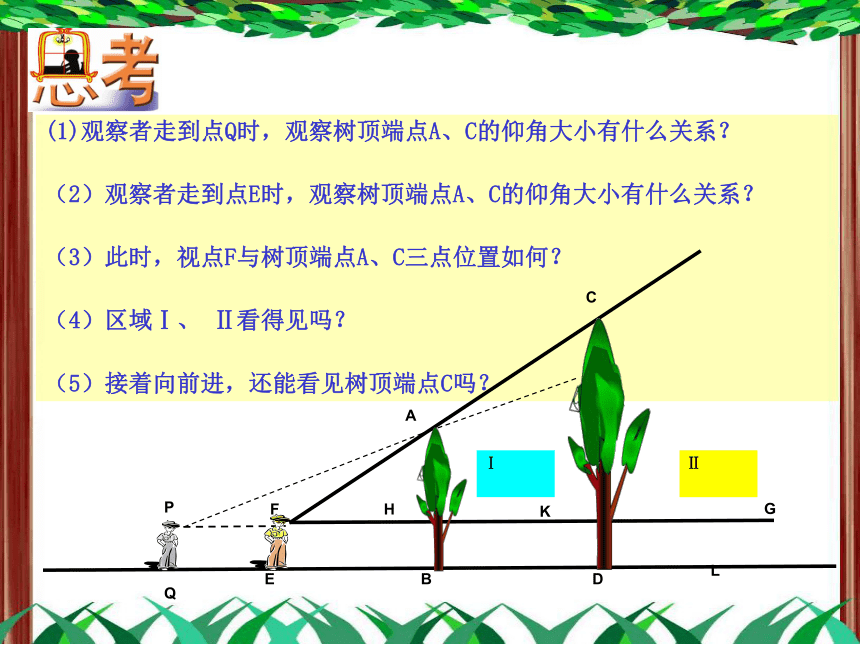
(1)观察者走到点Q时,观察树顶端点A、C的仰角大小有什么关系?
(2)观察者走到点E时,观察树顶端点A、C的仰角大小有什么关系?
(3)此时,视点F与树顶端点A、C三点位置如何?
(4)区域Ⅰ、 Ⅱ看得见吗?
(5)接着向前进,还能看见树顶端点C吗?
D
B
G
F
C
A
E
H
P
Q
K
Ⅰ
Ⅱ
L
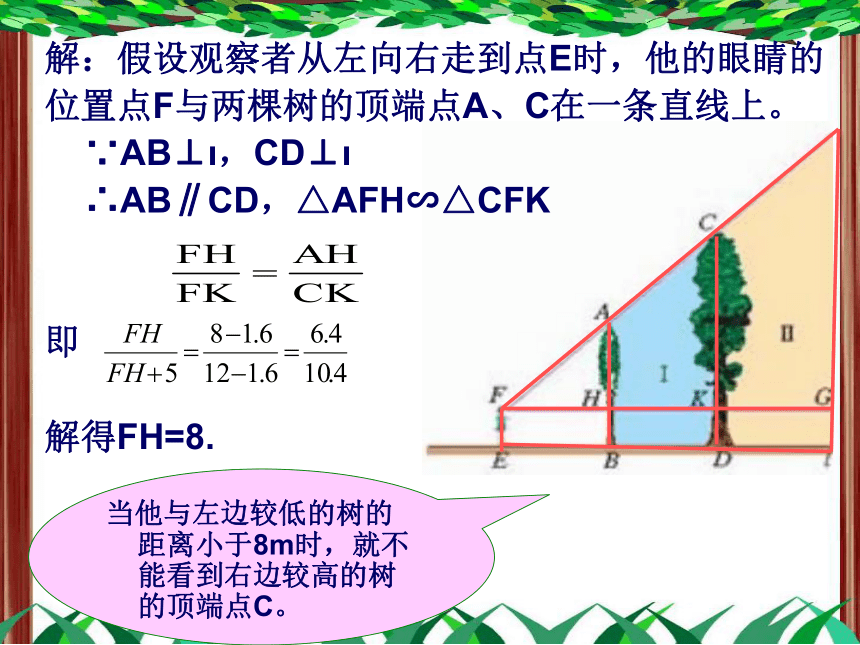
当他与左边较低的树的距离小于8m时,就不能看到右边较高的树的顶端点C。
解:假设观察者从左向右走到点E时,他的眼睛的
位置点F与两棵树的顶端点A、C在一条直线上。
∵AB⊥ι,CD⊥ι
∴AB∥CD,△AFH∽△CFK
即
解得FH=8.
正在观看升旗仪式的小明很想知道旗杆的高度,又很难直接测量,你能帮帮他吗?
你能设计方案,利用相似三角形的有关知识测量旗杆的高度吗?
1、利用自然常识及其他学科知识设计测量方案,方案中突出体现利用相似三角形的知识,通过构造相似三角形模型解决旗杆高度的测量问题,画出方案设计图。
2、指明构造相似三角形的依据。
3、标注需要测量的数据,可以测量的边长可用字母a、b、c 、d表示,要求的边长可用未知数x表示。
4、小组交流,利用相似三角形的知识解决问题的步骤。
(学生小组讨论,画好方案设计图后,准备班级展示。)
方案1:利用阳光下的影子
C
A
E
B
D
方案2:利用标杆
A
C
B
E
F
F
C
A
B
E
D
G
H
方案3:利用平面镜
E
C
B
D
A
A
E
D
B
C
.
C
A
E
B
D
A
C
B
E
F
E
C
B
D
A
构造 相似三角形 找出比例式
代入数据 计算求解
1、若学生身高是1.6m,其影长是2m,旗杆影长5m,
求旗杆高度。
A
F
若学生身高是1.6m,其影长是2m,
变式:如果旗杆前有一幢楼房,影子不全落在地面上,有一部分落在墙上,测得落在地面上的影长为1m,留在墙上的影长为3.2m,求旗杆的高。
C
B
G
H
A
1.6m
2m
D
E
F
2、若学生眼睛距地面高度是1.6m,标杆是2m,学生距标杆1m,标杆底部距旗杆底部是5m,求旗杆高度。
3、若学生眼睛距地面高度是1.6m,学生脚距镜子2m,镜子距旗杆底部是5m,求旗杆高度。
在实际生活中, 我们面对不能直接测量物体的高度和宽度时,应该怎么办呢?说说你在本节课的收获。
一、解决实际问题时,首先要把实际问题转化为几何模型即建模,再利用三角形相似的相关知识来解决。
二、步骤:构造 相似三角形 找出比例式 代入数据 计算求解
独立
作业
1、必做题:教材P55 9、10
2、选做题:
一盗窃犯于夜深人静之时潜入某单位作案,该单位的自动摄像系统摄下了他作案时的全过程。请你为警方设计一个方案,估计该盗窃犯的大致身高。
参考方案:选取罪犯直立时的影像并量取长度,再选当时室内一参照物并量取参照物实际高度和它影像的高度,由罪犯实际身高∶罪犯影像长=参照物实际高度∶参照物影像高度.可得罪犯实际身高。
3、备选题:
以组为单位完成一份实践报告。活动内容是:测量我校教学楼的高度。
以事先分好的四大组进行活动,每组分别实施三种方法,要求每小组中有观测员,测量员,记录员,运算员,复查员。
结束寄语
数学源于生活,又反过来服务于生活。如果你无愧于数学,那数学就可以助你到达胜利的彼岸。
(2)如图1,小强站在楼下能看到3楼窗口内的小明吗?为什么?
(3)你认为小强站在什么位置时,才能看到小明?
在进行测量时,从下向上看,视线与水平视线的夹角叫做仰角。
水平视线
视线
观察者眼晴的位置为视点。
观察者看不到的区域为盲区。
仰角
王鹏为了测量校园内一棵大树的高度,他在大树前处竖了一根标杆CD(如图所示),然后他往后退,当他退至B处,看到标杆顶端C恰好挡住了大树顶端E时,三点在同一条直线上。你认为他这样做能测出树高吗?如果可以,请说明理由;如果不可以,请说明为什么?
E
F
C
D
A
B
G
H
A
H
E
C
G
EF =FH + EH = AB+EH
即: 大树高
∵ △ACG∽△AEH
∴ =
A G CG
AH EH
例5 已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m,一个身高1.6m的人沿着正对这两棵树的一条水平直路L从左向右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C?
D
B
G
F
C
A
E
H
P
Q
K
Ⅰ
Ⅱ
L
(1)观察者走到点Q时,观察树顶端点A、C的仰角大小有什么关系?
(2)观察者走到点E时,观察树顶端点A、C的仰角大小有什么关系?
(3)此时,视点F与树顶端点A、C三点位置如何?
(4)区域Ⅰ、 Ⅱ看得见吗?
(5)接着向前进,还能看见树顶端点C吗?
D
B
G
F
C
A
E
H
P
Q
K
Ⅰ
Ⅱ
L
当他与左边较低的树的距离小于8m时,就不能看到右边较高的树的顶端点C。
解:假设观察者从左向右走到点E时,他的眼睛的
位置点F与两棵树的顶端点A、C在一条直线上。
∵AB⊥ι,CD⊥ι
∴AB∥CD,△AFH∽△CFK
即
解得FH=8.
正在观看升旗仪式的小明很想知道旗杆的高度,又很难直接测量,你能帮帮他吗?
你能设计方案,利用相似三角形的有关知识测量旗杆的高度吗?
1、利用自然常识及其他学科知识设计测量方案,方案中突出体现利用相似三角形的知识,通过构造相似三角形模型解决旗杆高度的测量问题,画出方案设计图。
2、指明构造相似三角形的依据。
3、标注需要测量的数据,可以测量的边长可用字母a、b、c 、d表示,要求的边长可用未知数x表示。
4、小组交流,利用相似三角形的知识解决问题的步骤。
(学生小组讨论,画好方案设计图后,准备班级展示。)
方案1:利用阳光下的影子
C
A
E
B
D
方案2:利用标杆
A
C
B
E
F
F
C
A
B
E
D
G
H
方案3:利用平面镜
E
C
B
D
A
A
E
D
B
C
.
C
A
E
B
D
A
C
B
E
F
E
C
B
D
A
构造 相似三角形 找出比例式
代入数据 计算求解
1、若学生身高是1.6m,其影长是2m,旗杆影长5m,
求旗杆高度。
A
F
若学生身高是1.6m,其影长是2m,
变式:如果旗杆前有一幢楼房,影子不全落在地面上,有一部分落在墙上,测得落在地面上的影长为1m,留在墙上的影长为3.2m,求旗杆的高。
C
B
G
H
A
1.6m
2m
D
E
F
2、若学生眼睛距地面高度是1.6m,标杆是2m,学生距标杆1m,标杆底部距旗杆底部是5m,求旗杆高度。
3、若学生眼睛距地面高度是1.6m,学生脚距镜子2m,镜子距旗杆底部是5m,求旗杆高度。
在实际生活中, 我们面对不能直接测量物体的高度和宽度时,应该怎么办呢?说说你在本节课的收获。
一、解决实际问题时,首先要把实际问题转化为几何模型即建模,再利用三角形相似的相关知识来解决。
二、步骤:构造 相似三角形 找出比例式 代入数据 计算求解
独立
作业
1、必做题:教材P55 9、10
2、选做题:
一盗窃犯于夜深人静之时潜入某单位作案,该单位的自动摄像系统摄下了他作案时的全过程。请你为警方设计一个方案,估计该盗窃犯的大致身高。
参考方案:选取罪犯直立时的影像并量取长度,再选当时室内一参照物并量取参照物实际高度和它影像的高度,由罪犯实际身高∶罪犯影像长=参照物实际高度∶参照物影像高度.可得罪犯实际身高。
3、备选题:
以组为单位完成一份实践报告。活动内容是:测量我校教学楼的高度。
以事先分好的四大组进行活动,每组分别实施三种方法,要求每小组中有观测员,测量员,记录员,运算员,复查员。
结束寄语
数学源于生活,又反过来服务于生活。如果你无愧于数学,那数学就可以助你到达胜利的彼岸。
