3.4.2 电话计费问题 课件
图片预览



文档简介
——实际问题与一元一次方程
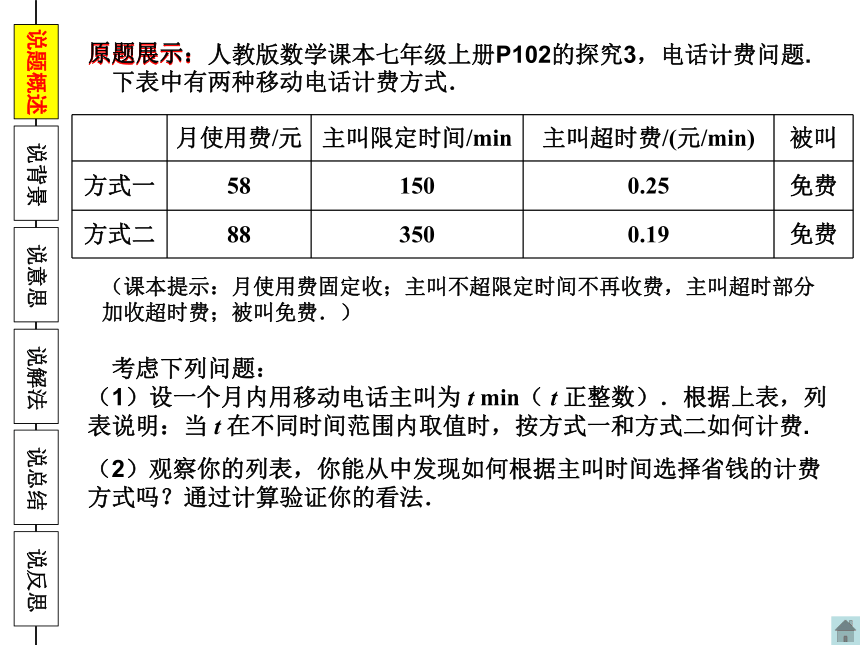
原题展示:人教版数学课本七年级上册P102的探究3,电话计费问题.
原题展示:
下表中有两种移动电话计费方式.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
(课本提示:月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.)
考虑下列问题:
(1)设一个月内用移动电话主叫为 t min( t 正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
说题概述
说背景
说意思
说解法
说总结
说反思
一、说题目的背景
二、说题目的意思
三、说题目的解法
四、说总结与拓展
——实际问题与一元一次方程
五、说本题的反思
说题概述
说背景
说意思
说解法
说总结
说反思
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
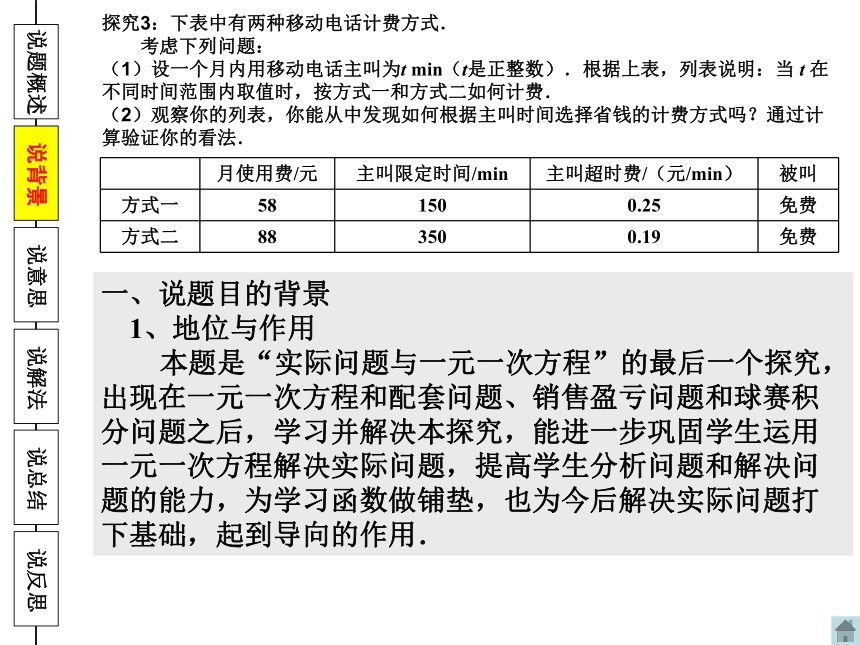
一、说题目的背景
1、地位与作用
本题是“实际问题与一元一次方程”的最后一个探究,出现在一元一次方程和配套问题、销售盈亏问题和球赛积分问题之后,学习并解决本探究,能进一步巩固学生运用一元一次方程解决实际问题,提高学生分析问题和解决问题的能力,为学习函数做铺垫,也为今后解决实际问题打下基础,起到导向的作用.
说题概述
说背景
说意思
说解法
说总结
说反思
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
一、说题目的背景
2、知识背景
探究包含了列代数式、解一元一次方程等知识.
3、思想、方法背景
通过表格和数形结合的方法,用方程、分类讨论和类比的思想解决探究.
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
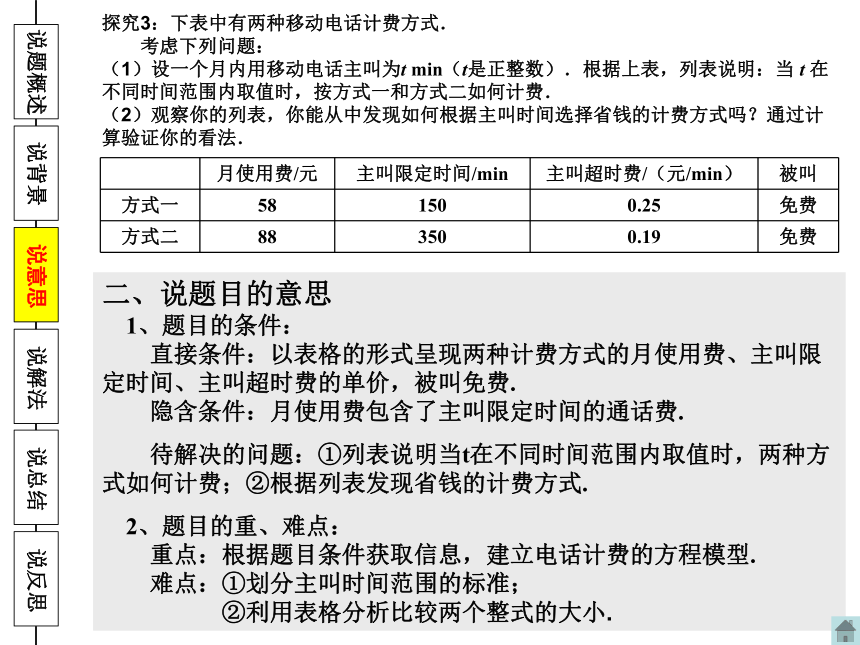
二、说题目的意思
1、题目的条件:
直接条件:以表格的形式呈现两种计费方式的月使用费、主叫限定时间、主叫超时费的单价,被叫免费.
隐含条件:月使用费包含了主叫限定时间的通话费.
待解决的问题:①列表说明当t在不同时间范围内取值时,两种方式如何计费;②根据列表发现省钱的计费方式.
2、题目的重、难点:
重点:根据题目条件获取信息,建立电话计费的方程模型.
难点:①划分主叫时间范围的标准;
②利用表格分析比较两个整式的大小.
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
二、说题目的意思
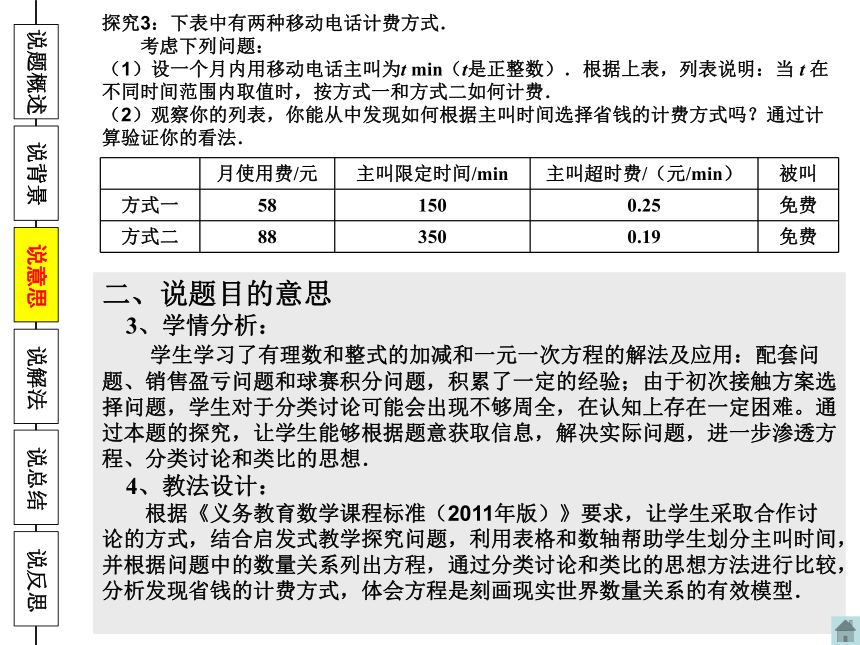
3、学情分析:
学生学习了有理数和整式的加减和一元一次方程的解法及应用:配套问题、销售盈亏问题和球赛积分问题,积累了一定的经验;由于初次接触方案选择问题,学生对于分类讨论可能会出现不够周全,在认知上存在一定困难。通过本题的探究,让学生能够根据题意获取信息,解决实际问题,进一步渗透方程、分类讨论和类比的思想.
4、教法设计:
根据《义务教育数学课程标准(2011年版)》要求,让学生采取合作讨论的方式,结合启发式教学探究问题,利用表格和数轴帮助学生划分主叫时间,并根据问题中的数量关系列出方程,通过分类讨论和类比的思想方法进行比较,分析发现省钱的计费方式,体会方程是刻画现实世界数量关系的有效模型.
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
三、说题目的解法
1、读题、审题
(1)明确基本量:①两种计费方式各自的月使用费;②主叫限定时间 ;③主叫超时费单价.
(2)明确题目要求的问题:①列表说明当 t 在不同时间范围内取值时,两种方式如何计费;②根据列表发现省钱的计费方式.
给出以下问题让学生合作讨论,交流探究:
1.阅读表格,要求学生用自己的话说明两种方式如何计费;
2.从表格中的数据,你会把主叫时间分为几个部分?为什么这样分?
3.你如何根据表格判断两种计费方式哪种更合算?
⑴
【教师提问】:你从数轴获取了哪些信息?你认为主叫时间t 可以分成哪些范围?
【教师提问】:由数轴图示发现0~150和0~350有重复的时间段,这时又如何划分主叫时间?
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
1.阅读表格,要求学生用自己的话说明两种方式如何计费.
【教师提问】:当t =100时,方式一如何计费?t =150、t =200时又如何计费?
通过计算和讨论发现计费与主叫时间有关,计费时首先要看主叫是否超过限定时间.得出方式一的计费分段:
(这里借助之前学习过的数轴的形式来直观表示)
说题概述
说背景
说意思
说解法
说总结
说反思
⑵
58 58+0.25(t-150)
150
t / min
0
88 88+0.19(t-350)
t / min
350
0
方式一:
方式二:
同样,可借助同一条数轴来表示这5段时间:
① ② ③ ④ ⑤
2.从表格中的数据,你会把主叫时间分为几个部分?为什么这样分?
学生一开始能得到的时间范围:t小于150/350min、t大于150/350min ,这时就要强调 t 等于150和350时的情况并进行范围的补充 ,通过观察分析数轴图示,发现还有150< t <350这段时间范围.
① t <150
② t =150
③ 150< t <350
④ t =350
⑤ t >350
说题概述
说背景
说意思
说解法
说总结
说反思
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
⑶
t / min
350
150
0
58 58+0.25(t-150)
150
t / min
0
88 88+0.19(t-350)
t / min
350
0
方式一:
方式二:
由于学生是初步接触表格设计,在解题过程中教师需进行适当的引导:表格需要3列(主叫时间、方式一计费、方式二计费);主叫时间分成5个部分,在标题下面再列出5行表格.
当 t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间 t /min
方式一计费/元
方式二计费/元
t <150
t=150
150< t <350
t=350
t >350
58
88
58
88
58+0.25(t-150)
88
108
88
58+0.25(t-150)
88+0.19(t-350)
说题概述
说背景
说意思
说解法
说总结
说反思
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
主叫时间 t /min
方式一计费/元
方式二计费/元
t <150
t=150
150< t <350
t=350
t >350
88
88
58+0.25(t-150)
88
108
58+0.25(t-150)
88+0.19(t-350)
3.根据所列表格判断两种计费方式那种更合算.
【教师提问】:当t =200、t =300时两种方式计费分别是多少?
通过分析计算结果发现在t大于150并且小于350这段主叫时间内,可能存在某主叫时间按两种方式去计费是相等的,这就是等量关系.
58
58
88
说题概述
说背景
说意思
说解法
说总结
说反思
【教师提问】:随着主叫时间的增加,两种方式的计费如何变化?
【教师提问】:观察所列表格,你能判断哪些主叫时间范围中,方式一或方式二省钱?
观察所列表格可知:主叫时间超出限定时间越长,计费越多.当 t 小于或等于150时,按方式一的计费少;当 t =350时,按方式二的计费少.所以在解题过程中要将关注点放在t 大于150且小于350和 t 大于350这两个范围上.
⑷
主叫时间 t /min
方式一计费/元
方式二计费/元
t <150
t=150
150< t <350
t=350
t >350
58
88
58
88
58+0.25(t-150)
88
108
88
58+0.25(t-150)
88+0.19(t-350)
说题概述
说背景
说意思
说解法
说总结
说反思
列方程:58+0.25(t-150)=88.解得t=270.
即当t=270时,两种方式计费相等
综上所述:当 t <270时,方式一省钱
当 t =270时,两种方式计费相等.
主叫时间t/min
方式一计费/元
方式二计费/元
t <150
58
88
t =150
58
88
150< t <270
88
t =270
88
88
270< t <350
58+0.25(t-150)
t =350
108
88
t >350
58+0.25(t-150)
88+0.19(t-350)
58+0.25(t-150)
88
【教师提问】:观察表格,判断主叫时间大于150min且小于270min和大于270min且小于350min的时间范围哪种方式省钱.
⑸
主叫时间t/min
方式一计费/元
方式二计费/元
t <150
58
88
t =150
58
88
150< t <270
58+0.25(t-150)
88
t =270
88
88
270< t <350
58+0.25(t-150)
88
t =350
108
88
t >350
58+0.25(t-150)
88+0.19(t-350)
说题概述
说背景
说意思
说解法
说总结
说反思
【教师提问】:当t >350时如何比较哪种计费方式省钱?
【教师提问】:当t =350时两种方式的计费分别是多少?当t >350时两种计费方式的超时费分别是多少?
法一:通过表格直接比较两种方式超时的计费:方式一超时计费为每分钟增加0.25元,方式二超时计费为每分钟增加0.19元.
当 t =350时,方式一计费比方式二多20元;
当 t >350时,每增加一分钟主叫时间,方式一都要比方式二多支付0.06元,所以当t>350时,按方式二的计费少.
最后比较 t >350时两种方式的计费:
⑹
⑺
法二:当t>350时,方式一的计费变式为108+0.25(t-350),对比方式二的计费表达式88+0.19(t-350)中的各项,得出当t>350时,按方式二的计费少.
法三:当t>350时,方式一的计费变式为88+0.19(t-350)+[20+0.06(t-350)],对比方式二的计费表达式88+0.19(t-350),方式一多了20+0.06(t-350)的整式,得出当t>350时,按方式二的计费少的结论.
说题概述
说背景
说意思
说解法
说总结
说反思
最后比较 t >350时两种方式的计费:
主叫时间t/min
方式一计费/元
方式二计费/元
t <150
58
88
t =150
58
88
150< t <270
58+0.25(t-150)
88
t =270
88
88
270< t <350
58+0.25(t-150)
88
t =350
108
88
t >350
58+0.25(t-150)
88+0.19(t-350)
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
时,两种方式计费相等.
t <270
t >270
t = 270
说题概述
说背景
说意思
说解法
说总结
说反思
⑻
主叫时间t/min
方式一计费/元
方式二计费/元
t <150
58
88
t =150
58
88
150< t <270
58+0.25(t-150)
88
t =270
88
88
270< t <350
58+0.25(t-150)
88
t =350
108
88
t >350
58+0.25(t-150)
88+0.19(t-350)
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
四、说总结与拓展
(一)解题方法总结
理解题意,找出基本量及其关系;利用表格和数形结合的方法,结合所学知识判断主叫时间的分段;找到两种方式计费相等的等量关系列方程求解;通过分类讨论和类比法比较不同主叫时间段下哪种方式计费少.
⑼
(二)题目拓展引申
(课本P112拓广探究10)一家游泳馆每年6~8月出售夏季会员证,每张会员证80元,只限本人使用,凭证购入场券每张1元,不凭证购入场券每张3元.试讨论并回答:
(1)什么情况下,购会员证与不购证付一样的钱?
(2)什么情况下,购会员证比不购证更合算?
(3)什么情况下,不购会员证比购证更合算?
分析:本题是与探究3的相同点是都需要利用分类讨论和方程求出省钱的方案;区别在于题目背景由电话计费变成了购票方案.学生可借助表格明确题目条件,求出不同情况下的费用,给出省钱的方案.
会员证费用/元
入场券价格/(张/元)
总费用/元
购买会员证
80
1
不购买会员证
0
3
说题概述
说背景
说意思
说解法
说总结
说反思
电话计费问题
分类讨论
找等量关系
列一元一次方程
解方程,
得结果
说题概述
说背景
说意思
说解法
说总结
说反思
五、说本题的反思
本题综合性较强,以学生合作讨论的方式,教师采取启发式教学进行分析,在分析解题过程中设计了多个小问题,层层递进,将本题难度细分.
用学生已经学习过的数轴作为辅助,直观的表示出主叫时间的分段,简洁明了的向学生说明分析的思路.
在问题(2)的比较费用过程中,由于学生还没学习函数和不等式的相关知识,比较两个式子的大小只能通过具体数字的计算,或对比两式的各项来说明比较,在解题分析时就要明确类比的思想方法.
原题展示:人教版数学课本七年级上册P102的探究3,电话计费问题.
原题展示:
下表中有两种移动电话计费方式.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
(课本提示:月使用费固定收;主叫不超限定时间不再收费,主叫超时部分加收超时费;被叫免费.)
考虑下列问题:
(1)设一个月内用移动电话主叫为 t min( t 正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
说题概述
说背景
说意思
说解法
说总结
说反思
一、说题目的背景
二、说题目的意思
三、说题目的解法
四、说总结与拓展
——实际问题与一元一次方程
五、说本题的反思
说题概述
说背景
说意思
说解法
说总结
说反思
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
一、说题目的背景
1、地位与作用
本题是“实际问题与一元一次方程”的最后一个探究,出现在一元一次方程和配套问题、销售盈亏问题和球赛积分问题之后,学习并解决本探究,能进一步巩固学生运用一元一次方程解决实际问题,提高学生分析问题和解决问题的能力,为学习函数做铺垫,也为今后解决实际问题打下基础,起到导向的作用.
说题概述
说背景
说意思
说解法
说总结
说反思
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
一、说题目的背景
2、知识背景
探究包含了列代数式、解一元一次方程等知识.
3、思想、方法背景
通过表格和数形结合的方法,用方程、分类讨论和类比的思想解决探究.
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
二、说题目的意思
1、题目的条件:
直接条件:以表格的形式呈现两种计费方式的月使用费、主叫限定时间、主叫超时费的单价,被叫免费.
隐含条件:月使用费包含了主叫限定时间的通话费.
待解决的问题:①列表说明当t在不同时间范围内取值时,两种方式如何计费;②根据列表发现省钱的计费方式.
2、题目的重、难点:
重点:根据题目条件获取信息,建立电话计费的方程模型.
难点:①划分主叫时间范围的标准;
②利用表格分析比较两个整式的大小.
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
二、说题目的意思
3、学情分析:
学生学习了有理数和整式的加减和一元一次方程的解法及应用:配套问题、销售盈亏问题和球赛积分问题,积累了一定的经验;由于初次接触方案选择问题,学生对于分类讨论可能会出现不够周全,在认知上存在一定困难。通过本题的探究,让学生能够根据题意获取信息,解决实际问题,进一步渗透方程、分类讨论和类比的思想.
4、教法设计:
根据《义务教育数学课程标准(2011年版)》要求,让学生采取合作讨论的方式,结合启发式教学探究问题,利用表格和数轴帮助学生划分主叫时间,并根据问题中的数量关系列出方程,通过分类讨论和类比的思想方法进行比较,分析发现省钱的计费方式,体会方程是刻画现实世界数量关系的有效模型.
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
三、说题目的解法
1、读题、审题
(1)明确基本量:①两种计费方式各自的月使用费;②主叫限定时间 ;③主叫超时费单价.
(2)明确题目要求的问题:①列表说明当 t 在不同时间范围内取值时,两种方式如何计费;②根据列表发现省钱的计费方式.
给出以下问题让学生合作讨论,交流探究:
1.阅读表格,要求学生用自己的话说明两种方式如何计费;
2.从表格中的数据,你会把主叫时间分为几个部分?为什么这样分?
3.你如何根据表格判断两种计费方式哪种更合算?
⑴
【教师提问】:你从数轴获取了哪些信息?你认为主叫时间t 可以分成哪些范围?
【教师提问】:由数轴图示发现0~150和0~350有重复的时间段,这时又如何划分主叫时间?
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
1.阅读表格,要求学生用自己的话说明两种方式如何计费.
【教师提问】:当t =100时,方式一如何计费?t =150、t =200时又如何计费?
通过计算和讨论发现计费与主叫时间有关,计费时首先要看主叫是否超过限定时间.得出方式一的计费分段:
(这里借助之前学习过的数轴的形式来直观表示)
说题概述
说背景
说意思
说解法
说总结
说反思
⑵
58 58+0.25(t-150)
150
t / min
0
88 88+0.19(t-350)
t / min
350
0
方式一:
方式二:
同样,可借助同一条数轴来表示这5段时间:
① ② ③ ④ ⑤
2.从表格中的数据,你会把主叫时间分为几个部分?为什么这样分?
学生一开始能得到的时间范围:t小于150/350min、t大于150/350min ,这时就要强调 t 等于150和350时的情况并进行范围的补充 ,通过观察分析数轴图示,发现还有150< t <350这段时间范围.
① t <150
② t =150
③ 150< t <350
④ t =350
⑤ t >350
说题概述
说背景
说意思
说解法
说总结
说反思
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
⑶
t / min
350
150
0
58 58+0.25(t-150)
150
t / min
0
88 88+0.19(t-350)
t / min
350
0
方式一:
方式二:
由于学生是初步接触表格设计,在解题过程中教师需进行适当的引导:表格需要3列(主叫时间、方式一计费、方式二计费);主叫时间分成5个部分,在标题下面再列出5行表格.
当 t 在不同时间范围内取值时,方式一和方式二的计费如下表:
主叫时间 t /min
方式一计费/元
方式二计费/元
t <150
t=150
150< t <350
t=350
t >350
58
88
58
88
58+0.25(t-150)
88
108
88
58+0.25(t-150)
88+0.19(t-350)
说题概述
说背景
说意思
说解法
说总结
说反思
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
主叫时间 t /min
方式一计费/元
方式二计费/元
t <150
t=150
150< t <350
t=350
t >350
88
88
58+0.25(t-150)
88
108
58+0.25(t-150)
88+0.19(t-350)
3.根据所列表格判断两种计费方式那种更合算.
【教师提问】:当t =200、t =300时两种方式计费分别是多少?
通过分析计算结果发现在t大于150并且小于350这段主叫时间内,可能存在某主叫时间按两种方式去计费是相等的,这就是等量关系.
58
58
88
说题概述
说背景
说意思
说解法
说总结
说反思
【教师提问】:随着主叫时间的增加,两种方式的计费如何变化?
【教师提问】:观察所列表格,你能判断哪些主叫时间范围中,方式一或方式二省钱?
观察所列表格可知:主叫时间超出限定时间越长,计费越多.当 t 小于或等于150时,按方式一的计费少;当 t =350时,按方式二的计费少.所以在解题过程中要将关注点放在t 大于150且小于350和 t 大于350这两个范围上.
⑷
主叫时间 t /min
方式一计费/元
方式二计费/元
t <150
t=150
150< t <350
t=350
t >350
58
88
58
88
58+0.25(t-150)
88
108
88
58+0.25(t-150)
88+0.19(t-350)
说题概述
说背景
说意思
说解法
说总结
说反思
列方程:58+0.25(t-150)=88.解得t=270.
即当t=270时,两种方式计费相等
综上所述:当 t <270时,方式一省钱
当 t =270时,两种方式计费相等.
主叫时间t/min
方式一计费/元
方式二计费/元
t <150
58
88
t =150
58
88
150< t <270
88
t =270
88
88
270< t <350
58+0.25(t-150)
t =350
108
88
t >350
58+0.25(t-150)
88+0.19(t-350)
58+0.25(t-150)
88
【教师提问】:观察表格,判断主叫时间大于150min且小于270min和大于270min且小于350min的时间范围哪种方式省钱.
⑸
主叫时间t/min
方式一计费/元
方式二计费/元
t <150
58
88
t =150
58
88
150< t <270
58+0.25(t-150)
88
t =270
88
88
270< t <350
58+0.25(t-150)
88
t =350
108
88
t >350
58+0.25(t-150)
88+0.19(t-350)
说题概述
说背景
说意思
说解法
说总结
说反思
【教师提问】:当t >350时如何比较哪种计费方式省钱?
【教师提问】:当t =350时两种方式的计费分别是多少?当t >350时两种计费方式的超时费分别是多少?
法一:通过表格直接比较两种方式超时的计费:方式一超时计费为每分钟增加0.25元,方式二超时计费为每分钟增加0.19元.
当 t =350时,方式一计费比方式二多20元;
当 t >350时,每增加一分钟主叫时间,方式一都要比方式二多支付0.06元,所以当t>350时,按方式二的计费少.
最后比较 t >350时两种方式的计费:
⑹
⑺
法二:当t>350时,方式一的计费变式为108+0.25(t-350),对比方式二的计费表达式88+0.19(t-350)中的各项,得出当t>350时,按方式二的计费少.
法三:当t>350时,方式一的计费变式为88+0.19(t-350)+[20+0.06(t-350)],对比方式二的计费表达式88+0.19(t-350),方式一多了20+0.06(t-350)的整式,得出当t>350时,按方式二的计费少的结论.
说题概述
说背景
说意思
说解法
说总结
说反思
最后比较 t >350时两种方式的计费:
主叫时间t/min
方式一计费/元
方式二计费/元
t <150
58
88
t =150
58
88
150< t <270
58+0.25(t-150)
88
t =270
88
88
270< t <350
58+0.25(t-150)
88
t =350
108
88
t >350
58+0.25(t-150)
88+0.19(t-350)
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
时,两种方式计费相等.
t <270
t >270
t = 270
说题概述
说背景
说意思
说解法
说总结
说反思
⑻
主叫时间t/min
方式一计费/元
方式二计费/元
t <150
58
88
t =150
58
88
150< t <270
58+0.25(t-150)
88
t =270
88
88
270< t <350
58+0.25(t-150)
88
t =350
108
88
t >350
58+0.25(t-150)
88+0.19(t-350)
探究3:下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月内用移动电话主叫为t min(t是正整数).根据上表,列表说明:当 t 在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
说题概述
说背景
说意思
说解法
说总结
说反思
四、说总结与拓展
(一)解题方法总结
理解题意,找出基本量及其关系;利用表格和数形结合的方法,结合所学知识判断主叫时间的分段;找到两种方式计费相等的等量关系列方程求解;通过分类讨论和类比法比较不同主叫时间段下哪种方式计费少.
⑼
(二)题目拓展引申
(课本P112拓广探究10)一家游泳馆每年6~8月出售夏季会员证,每张会员证80元,只限本人使用,凭证购入场券每张1元,不凭证购入场券每张3元.试讨论并回答:
(1)什么情况下,购会员证与不购证付一样的钱?
(2)什么情况下,购会员证比不购证更合算?
(3)什么情况下,不购会员证比购证更合算?
分析:本题是与探究3的相同点是都需要利用分类讨论和方程求出省钱的方案;区别在于题目背景由电话计费变成了购票方案.学生可借助表格明确题目条件,求出不同情况下的费用,给出省钱的方案.
会员证费用/元
入场券价格/(张/元)
总费用/元
购买会员证
80
1
不购买会员证
0
3
说题概述
说背景
说意思
说解法
说总结
说反思
电话计费问题
分类讨论
找等量关系
列一元一次方程
解方程,
得结果
说题概述
说背景
说意思
说解法
说总结
说反思
五、说本题的反思
本题综合性较强,以学生合作讨论的方式,教师采取启发式教学进行分析,在分析解题过程中设计了多个小问题,层层递进,将本题难度细分.
用学生已经学习过的数轴作为辅助,直观的表示出主叫时间的分段,简洁明了的向学生说明分析的思路.
在问题(2)的比较费用过程中,由于学生还没学习函数和不等式的相关知识,比较两个式子的大小只能通过具体数字的计算,或对比两式的各项来说明比较,在解题分析时就要明确类比的思想方法.
