1.3函数的基本性质
图片预览







文档简介
(共51张PPT)
单调性与最大(小)值
——函数的单调性
1.3.1
新课导入
一、情景问题
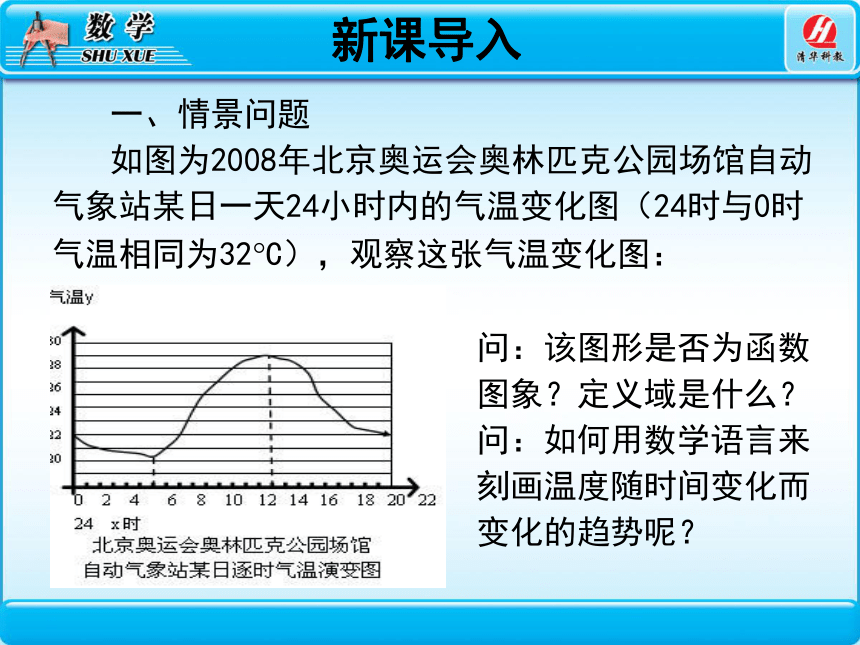
如图为2008年北京奥运会奥林匹克公园场馆自动气象站某日一天24小时内的气温变化图(24时与0时气温相同为32 C),观察这张气温变化图:
问:该图形是否为函数图象?定义域是什么?
问:如何用数学语言来刻画温度随时间变化而变化的趋势呢?
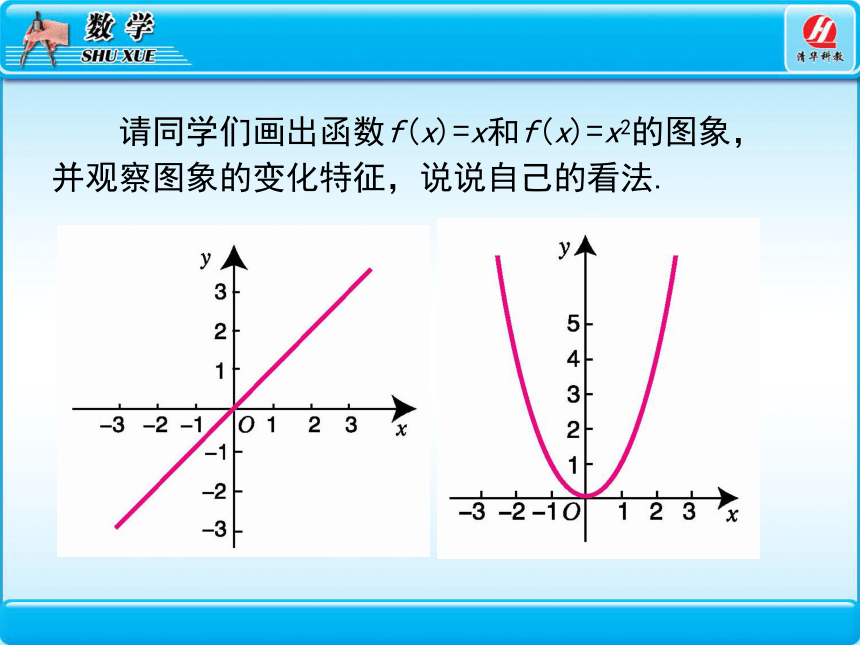
请同学们画出函数f(x)=x和f(x)=x2的图象,并观察图象的变化特征,说说自己的看法.
可观察到的图象特征:
(1)函数f(x)=x的图象由左至右是上升的;
(2)函数f(x)=x2的图象在y轴左侧是下降的,在y轴右侧是上升的;也就是图象在区间(-∞,0]上,随x着的增大,相应的f(x) 随着减小,在区间(0,+∞)上,随着x的增大,相应的f(x)也随着增大.
归纳:从上面的观察分析可以看出:不同的函数,其图象的变化趋势不同,同一函数在不同区间上的变化趋势也不同.函数图象的这种变化规律就是函数性质的反映.
思考:
1.如何用函数解析式f(x)=x2描述“随着x的增大,相应的f(x)随着减小”,“随着x的增大,相应的f(x)也随着增大”?
2.在区间(0,+∞)上任取x1,x2,函数值的大小变化与自变量的大小变化有何关系?如何用数学符号语言来描述这种关系呢?
对于函数f(x)=x2 ,经过师生讨论得出:
在区间(0,+∞)上,任取两个x1,x2,当x1 x2时,有f(x1) f(x2).这时,我们就说函数f(x)=x2在区间(0,+∞)上是增函数.
请你仿照刚才的描述,说明函数f(x)=x2在区间(-∞,0)上是减函数.
新课
一、函数的单调性
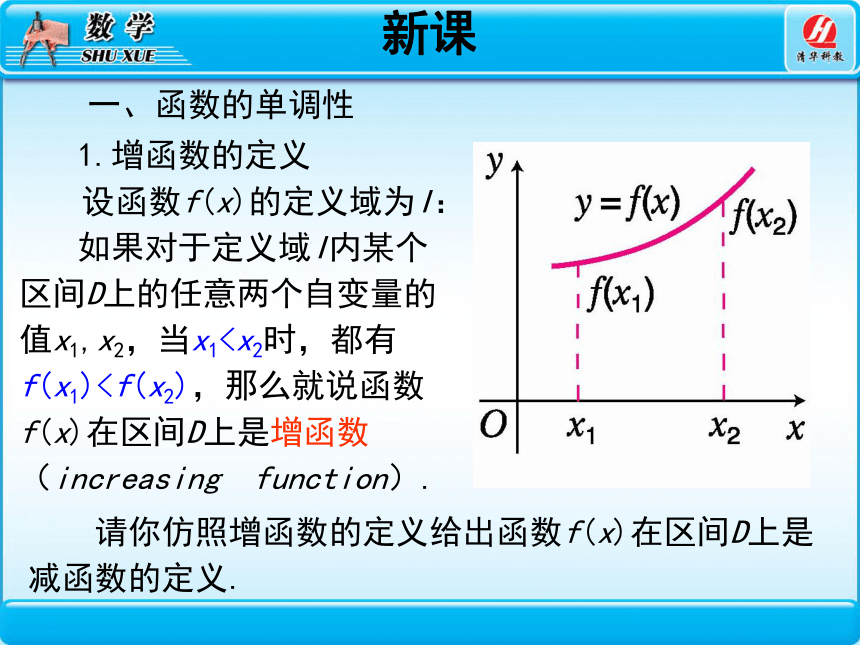
1.增函数的定义
设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1请你仿照增函数的定义给出函数f(x)在区间D上是减函数的定义.
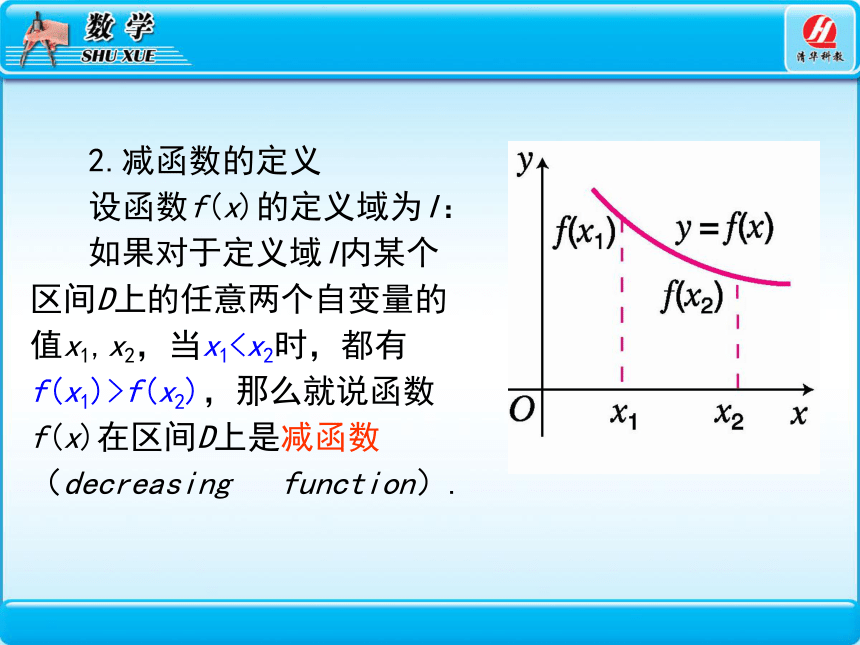
2.减函数的定义
设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1f(x2),那么就说函数f(x)在区间D上是减函数(decreasing function).
3.对定义要点分析
1) 函数是增函数还是减函数,是对定义域内某个区间而言的;
2)应是该区间内任意的两个实数,忽略需要任意取值这个条件,就不能保证函数是增函数(或减函数).
3.对定义要点分析
3)如果函数y=f(x)在某一区间D上是增(减)函数,就说f(x)在这个区间D上具有单调函数,
这一区间D叫做f(x)的单调区间.
说明:
(1)函数的单调区间D是其定义域I的子集;
(2)判断函数的单调性的方法:
比较法(要注意变形的程度)
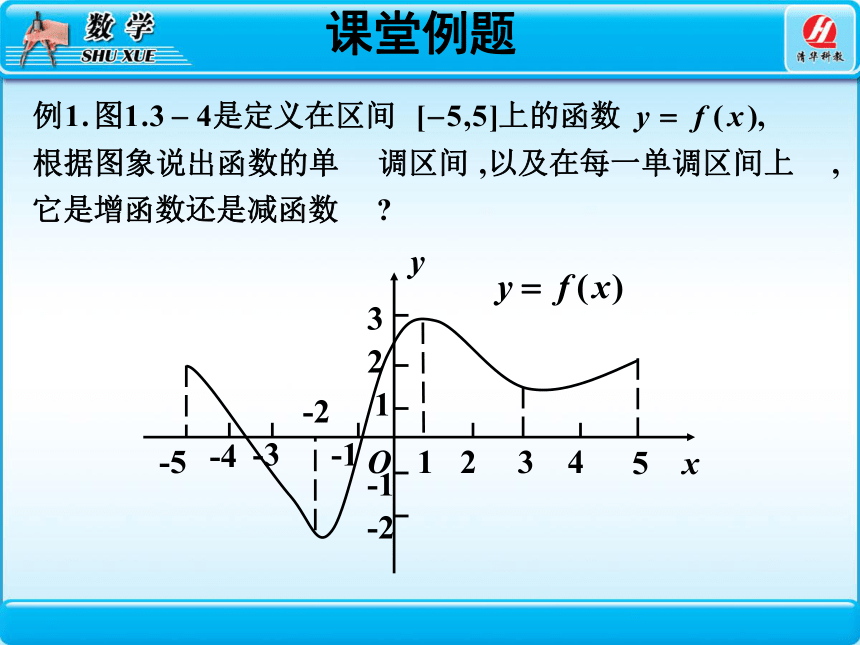
课堂例题
-5
-4
O
1
2
3
4
5
-1
-3
-2
-2
-1
1
2
3
x
y
课堂练习
1.一名心率过速患者服用某种药物后心率立刻明显减慢,之后随着药力的减退,心率再次慢慢升高.画出自服药那一刻起,心率关于时间的一个可能的图象(示意图).
2. 请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.
工人数
生产效率
O
3. 整个上午(8:00~12:00)天气越来越暖,中午时分(12:00~13:00)一场暴风雨使天气骤然凉爽了许多.暴风雨过后,天气转暖,直到太阳落山(18:00)才又开始转凉.画出这一天8:00~20:00期间气温作为时间函数的一个可能的图象,并说出所画函数的单调区间.
4. 根据下图说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数.
-1
1
2
3
4
5
1
2
3
4
5
6
7
O
x
y
课堂小结
(1)增减函数的图象有什么特点?增函数的图象从左自右是上升的,减函数的图象从左自右是下降的.
(2)用定义证明函数的单调性,需要抓住要点“在给定区间任意取两个自变量”去比较它们的函数值的大小.
(3)如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
课后作业
课本第39页习题1.3A组第1、2、3题.
课本第44页复习参考题A组第9题.
单调性与最大(小)值
—函数的最大(小)值
1.3.1
-5
-4
O
1
2
3
4
5
-1
-3
-2
-2
-1
1
2
3
x
y
发现,函数图象在x=-2时,其函数值最小,
而在x=1时,其函数值最大.
-5
-4
O
1
2
3
4
5
-1
-3
-2
-2
-1
1
2
3
x
y
观察f(x)=x2的图象
有一个最低点
观察f(x)=-x2的图象
x
y
O
有一个最高点
观察函数f(x)=x的图象
发现,没有最低点,也没有最高点.
新课
函数的最大(小)值
1.函数的最大(小)值的定义
设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0 ∈I ,使得f(x0)=M.
那么,我们称M是函数y=f(x)的最大值(maximum
value)。
请你仿造函数最大值的定义,给出是函数y=f(x)的最小值的定义.
设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0 ∈I ,使得f(x0)=M.
那么,我们称M是函数y=f(x)的最小值(minimum value).
课堂例题
例1. “菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度h m与时间t s之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?
课堂练习
1. 设f(x)是定义在区间[-6,11]上的函数.如果f(x)在区间[-6,-2]上递减,在区间[-2,11]上递增,画出f(x)的一个大致的图象,从图象上可以发现f(-2)是函数f(x)的一个__________________.
2.函数的最大(小)值与单调性的关系
从上面的例题可以看到,函数的最大(小)值与单调性有非常紧密的关系.
我们再看一个例子.
例3 观察下图,用函数的单调性研究以下问题:
(1) 若函数y=f(x)的定义域为x∈[b,e],求
最大值和最小值;
例3 观察下图,用函数的单调性研究以下问题:
(2) 若函数y=f(x)的定义域为x∈[a,e],求最
大值和最小值;
例3观察下图,用函数的单调性研究以下问题:
(3) 若函数y=f(x)的定义域为x∈[b,d),求最
大值和最小值;
课堂小结
函数的最大(小)值是一个函数在一段区间或者整个定义域上的整体性质.一个函数可能存在最大值也可能不存在最大值,最大值具有唯一性,对于最小值也一样.
我们经常利用函数的单调性求函数的最大(小)值.
课后作业
课本第39页习题1.3A组第5题;
课本第39页习题1.3B组第1、2题.
1.3.2 奇偶性
导入新课
从对称的角度,观察下列函数的图象:
函数f(x)=x2,g(x)=|x|
这两个函数图象有什么共同的特征
请列出从 3到3这一段区间上,两个函数的对应值表,并思考:自变量取值互为相反数时,函数值如何变化,有怎样的等量关系?
请列出从 3到3这一段区间上,两个函数的对应值表,并思考:自变量取值互为相反数时,函数值如何变化,有怎样的等量关系?
讨论结果:当自变量取值互为相反数时,函数值恰相等.
反映在图象上,函数图象关于y 轴对称.
新课
1.偶函数
如果函数f(x)的定义域内任意一个x,都有f(-
x)=f(x),那么函数f(x)就叫做偶函数(even
function).
定义域关于坐标原点对称.
请你举出偶函数的例子.
观察函数f(x)=x和 的图象,说一说这两个函数有什么共同特征?
(1)图象看,它们都是关于坐标原点成中心对称;
(2)从定义域看,它们的定义域都是关于坐标原点对称;
(3)从函数值看,x与-x的函数值的绝对值相等且符号相反.
2.奇函数
如果函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(old function).
定义域关于坐标原点对称.
请你举出奇函数的例子.
3.函数的奇偶性
奇函数和偶函数的这种性质叫做函数的奇偶性.
(1)具有奇偶性的函数的定义域具有对称性,即关于坐标原点对称,如果一个函数的定义域关于坐标原点不对称,就不具有奇偶性.
(2)具有奇偶性的函数的图象具有对称性.偶函数的图象关于y轴对称,奇函数的图象关于坐标原点对称;反之,如果一个函数的图象关于y轴对称,那么,这个函数是偶函数,如果一个函数的图象关于坐标原点对称,那么,这个函数是奇函数.
(3)由于奇函数和偶函数的对称性质,我们在研究函数时,只要知道一半定义域上的图象和性质,就可以得到另一半定义域上的图象和性质.
课堂练习
课堂练习
x
O
y
f(x)
x
O
y
g(x)
课堂小结
本节课学习了函数的奇偶性及其判断方法.我们可以把对称性和奇偶性结合起来思考.
定义域具有对称性,函数值具有对称性,图象具有对称性.由于奇函数和偶函数的对称性质,我们在研究函数时,只要知道一半定义域上的图象和性质,就可以得到另一半定义域上的图象和性质.
课后作业
课本第39页习题1.3A组第6题,B组第3题.
课本第44页复习参考题A组第10题.
课后作业
单调性与最大(小)值
——函数的单调性
1.3.1
新课导入
一、情景问题
如图为2008年北京奥运会奥林匹克公园场馆自动气象站某日一天24小时内的气温变化图(24时与0时气温相同为32 C),观察这张气温变化图:
问:该图形是否为函数图象?定义域是什么?
问:如何用数学语言来刻画温度随时间变化而变化的趋势呢?
请同学们画出函数f(x)=x和f(x)=x2的图象,并观察图象的变化特征,说说自己的看法.
可观察到的图象特征:
(1)函数f(x)=x的图象由左至右是上升的;
(2)函数f(x)=x2的图象在y轴左侧是下降的,在y轴右侧是上升的;也就是图象在区间(-∞,0]上,随x着的增大,相应的f(x) 随着减小,在区间(0,+∞)上,随着x的增大,相应的f(x)也随着增大.
归纳:从上面的观察分析可以看出:不同的函数,其图象的变化趋势不同,同一函数在不同区间上的变化趋势也不同.函数图象的这种变化规律就是函数性质的反映.
思考:
1.如何用函数解析式f(x)=x2描述“随着x的增大,相应的f(x)随着减小”,“随着x的增大,相应的f(x)也随着增大”?
2.在区间(0,+∞)上任取x1,x2,函数值的大小变化与自变量的大小变化有何关系?如何用数学符号语言来描述这种关系呢?
对于函数f(x)=x2 ,经过师生讨论得出:
在区间(0,+∞)上,任取两个x1,x2,当x1 x2时,有f(x1) f(x2).这时,我们就说函数f(x)=x2在区间(0,+∞)上是增函数.
请你仿照刚才的描述,说明函数f(x)=x2在区间(-∞,0)上是减函数.
新课
一、函数的单调性
1.增函数的定义
设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1
2.减函数的定义
设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1
3.对定义要点分析
1) 函数是增函数还是减函数,是对定义域内某个区间而言的;
2)应是该区间内任意的两个实数,忽略需要任意取值这个条件,就不能保证函数是增函数(或减函数).
3.对定义要点分析
3)如果函数y=f(x)在某一区间D上是增(减)函数,就说f(x)在这个区间D上具有单调函数,
这一区间D叫做f(x)的单调区间.
说明:
(1)函数的单调区间D是其定义域I的子集;
(2)判断函数的单调性的方法:
比较法(要注意变形的程度)
课堂例题
-5
-4
O
1
2
3
4
5
-1
-3
-2
-2
-1
1
2
3
x
y
课堂练习
1.一名心率过速患者服用某种药物后心率立刻明显减慢,之后随着药力的减退,心率再次慢慢升高.画出自服药那一刻起,心率关于时间的一个可能的图象(示意图).
2. 请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.
工人数
生产效率
O
3. 整个上午(8:00~12:00)天气越来越暖,中午时分(12:00~13:00)一场暴风雨使天气骤然凉爽了许多.暴风雨过后,天气转暖,直到太阳落山(18:00)才又开始转凉.画出这一天8:00~20:00期间气温作为时间函数的一个可能的图象,并说出所画函数的单调区间.
4. 根据下图说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数.
-1
1
2
3
4
5
1
2
3
4
5
6
7
O
x
y
课堂小结
(1)增减函数的图象有什么特点?增函数的图象从左自右是上升的,减函数的图象从左自右是下降的.
(2)用定义证明函数的单调性,需要抓住要点“在给定区间任意取两个自变量”去比较它们的函数值的大小.
(3)如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
课后作业
课本第39页习题1.3A组第1、2、3题.
课本第44页复习参考题A组第9题.
单调性与最大(小)值
—函数的最大(小)值
1.3.1
-5
-4
O
1
2
3
4
5
-1
-3
-2
-2
-1
1
2
3
x
y
发现,函数图象在x=-2时,其函数值最小,
而在x=1时,其函数值最大.
-5
-4
O
1
2
3
4
5
-1
-3
-2
-2
-1
1
2
3
x
y
观察f(x)=x2的图象
有一个最低点
观察f(x)=-x2的图象
x
y
O
有一个最高点
观察函数f(x)=x的图象
发现,没有最低点,也没有最高点.
新课
函数的最大(小)值
1.函数的最大(小)值的定义
设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0 ∈I ,使得f(x0)=M.
那么,我们称M是函数y=f(x)的最大值(maximum
value)。
请你仿造函数最大值的定义,给出是函数y=f(x)的最小值的定义.
设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≥M;
(2)存在x0 ∈I ,使得f(x0)=M.
那么,我们称M是函数y=f(x)的最小值(minimum value).
课堂例题
例1. “菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度h m与时间t s之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?
课堂练习
1. 设f(x)是定义在区间[-6,11]上的函数.如果f(x)在区间[-6,-2]上递减,在区间[-2,11]上递增,画出f(x)的一个大致的图象,从图象上可以发现f(-2)是函数f(x)的一个__________________.
2.函数的最大(小)值与单调性的关系
从上面的例题可以看到,函数的最大(小)值与单调性有非常紧密的关系.
我们再看一个例子.
例3 观察下图,用函数的单调性研究以下问题:
(1) 若函数y=f(x)的定义域为x∈[b,e],求
最大值和最小值;
例3 观察下图,用函数的单调性研究以下问题:
(2) 若函数y=f(x)的定义域为x∈[a,e],求最
大值和最小值;
例3观察下图,用函数的单调性研究以下问题:
(3) 若函数y=f(x)的定义域为x∈[b,d),求最
大值和最小值;
课堂小结
函数的最大(小)值是一个函数在一段区间或者整个定义域上的整体性质.一个函数可能存在最大值也可能不存在最大值,最大值具有唯一性,对于最小值也一样.
我们经常利用函数的单调性求函数的最大(小)值.
课后作业
课本第39页习题1.3A组第5题;
课本第39页习题1.3B组第1、2题.
1.3.2 奇偶性
导入新课
从对称的角度,观察下列函数的图象:
函数f(x)=x2,g(x)=|x|
这两个函数图象有什么共同的特征
请列出从 3到3这一段区间上,两个函数的对应值表,并思考:自变量取值互为相反数时,函数值如何变化,有怎样的等量关系?
请列出从 3到3这一段区间上,两个函数的对应值表,并思考:自变量取值互为相反数时,函数值如何变化,有怎样的等量关系?
讨论结果:当自变量取值互为相反数时,函数值恰相等.
反映在图象上,函数图象关于y 轴对称.
新课
1.偶函数
如果函数f(x)的定义域内任意一个x,都有f(-
x)=f(x),那么函数f(x)就叫做偶函数(even
function).
定义域关于坐标原点对称.
请你举出偶函数的例子.
观察函数f(x)=x和 的图象,说一说这两个函数有什么共同特征?
(1)图象看,它们都是关于坐标原点成中心对称;
(2)从定义域看,它们的定义域都是关于坐标原点对称;
(3)从函数值看,x与-x的函数值的绝对值相等且符号相反.
2.奇函数
如果函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数(old function).
定义域关于坐标原点对称.
请你举出奇函数的例子.
3.函数的奇偶性
奇函数和偶函数的这种性质叫做函数的奇偶性.
(1)具有奇偶性的函数的定义域具有对称性,即关于坐标原点对称,如果一个函数的定义域关于坐标原点不对称,就不具有奇偶性.
(2)具有奇偶性的函数的图象具有对称性.偶函数的图象关于y轴对称,奇函数的图象关于坐标原点对称;反之,如果一个函数的图象关于y轴对称,那么,这个函数是偶函数,如果一个函数的图象关于坐标原点对称,那么,这个函数是奇函数.
(3)由于奇函数和偶函数的对称性质,我们在研究函数时,只要知道一半定义域上的图象和性质,就可以得到另一半定义域上的图象和性质.
课堂练习
课堂练习
x
O
y
f(x)
x
O
y
g(x)
课堂小结
本节课学习了函数的奇偶性及其判断方法.我们可以把对称性和奇偶性结合起来思考.
定义域具有对称性,函数值具有对称性,图象具有对称性.由于奇函数和偶函数的对称性质,我们在研究函数时,只要知道一半定义域上的图象和性质,就可以得到另一半定义域上的图象和性质.
课后作业
课本第39页习题1.3A组第6题,B组第3题.
课本第44页复习参考题A组第10题.
课后作业
