湘教版七年级数学下册课件:5.2 旋转(共16张ppt)
文档属性
| 名称 | 湘教版七年级数学下册课件:5.2 旋转(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 19:35:30 | ||
图片预览




文档简介
5.2 旋转
第5章 轴对称与旋转
情景引入
如图 ,观察钟表的指针,电风扇的叶片,汽车的雨刮器在转动的过程中有什么共同的特征.
钟表的指针绕中间的固定点旋转,电风扇的叶片绕电机的轴旋转,汽车的雨刮器绕支点旋转.
获取新知
将一个平面图形F上的每一个点,绕这个平面内一个定点O旋转同一个角α,(即把图形F上每一个点与定点的连线绕定点O旋转α),得到图形F',如图,图形的这种变换叫做旋转.这个定点 O 叫旋转中心,角α叫做旋转角.
原位置的图形F叫做原像,新位置的图形F'叫做图形F在旋转下的像. 图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点.
旋转的决定因素:
旋转中心、旋转角度、旋转方向
旋转的定义
α
获取新知
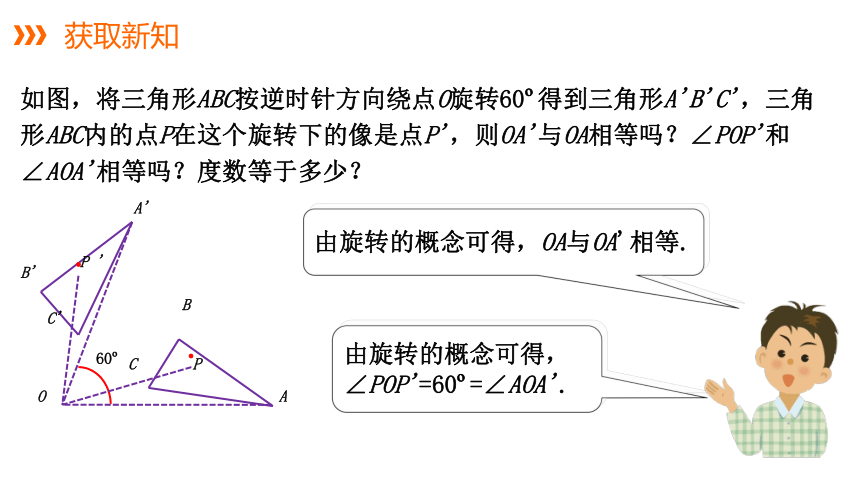
如图,将三角形ABC按逆时针方向绕点O旋转60?得到三角形A'B'C',三角形ABC内的点P在这个旋转下的像是点P',则OA'与OA相等吗?∠POP'和∠AOA'相等吗?度数等于多少?
A'
B'
C'
A
B
C
O
.
.
P '
P
60?
由旋转的概念可得,OA与OA'相等.
由旋转的概念可得,∠POP'=60?=∠AOA'.
获取新知
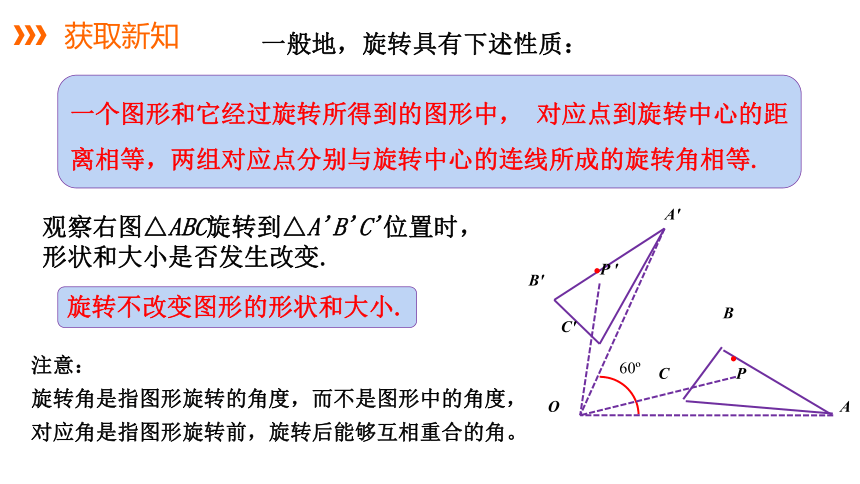
一般地,旋转具有下述性质:
A'
B'
C'
A
B
C
O
.
.
P '
P
60?
一个图形和它经过旋转所得到的图形中, 对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的旋转角相等.
观察右图△ABC旋转到△A'B'C'位置时,形状和大小是否发生改变.
旋转不改变图形的形状和大小.
注意:
旋转角是指图形旋转的角度,而不是图形中的角度,对应角是指图形旋转前,旋转后能够互相重合的角。
例题讲解
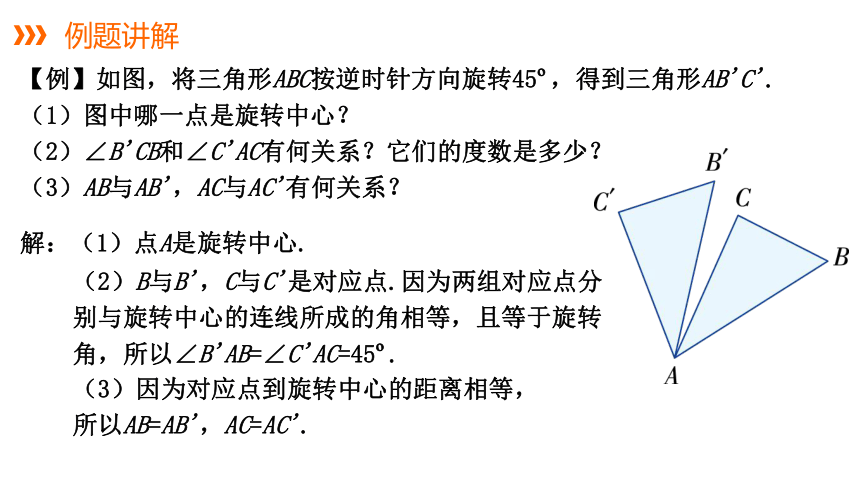
【例】如图,将三角形ABC按逆时针方向旋转45?,得到三角形AB'C'.
(1)图中哪一点是旋转中心?
(2)∠B'CB和∠C'AC有何关系?它们的度数是多少?
(3)AB与AB',AC与AC'有何关系?
解:(1)点A是旋转中心.
(2)B与B',C与C'是对应点.因为两组对应点分别与旋转中心的连线所成的角相等,且等于旋转角,所以∠B'AB=∠C'AC=45?.
(3)因为对应点到旋转中心的距离相等,所以AB=AB',AC=AC'.
获取新知
平行四边形绕中心旋转
获取新知
1、相同:
B
A
C
O
2、不同:
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或逆时针
转动一定的角度
平移和旋转的异同:
都是一种运动;运动前后 不改变图形的形状和大小
获取新知
三角形绕点旋转加平移
例题讲解
随堂演练
【归纳总结】旋转性质的“两应用”
(1)应用一:判断线段或角是否相等.
①根据旋转角相等,对应点与旋转中心的连线相等可得角或线段相等;
②根据旋转后的图形与原来图形的形状、大小都相同可得图形的对应线段、对应角相等.
(2)应用二:计算图形的面积、线段的长度或角的大小.
随堂演练
获取新知
作旋转变换后的图形:
(1)先确定图形的关键点和(定点)旋转中心
(2)分别连接关键点和定点
(3)利用旋转性质作出关键点的对应点(根据旋转方向和旋转角度作出)
(3)按照原图形中的连接方法顺次连接各对应点,要注意旋转中心,旋转方向和旋转角
随堂演练
A
B'
OB'
A'B'
∠A'
∠B'
O
60
随堂演练
垂直
40
4.钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心.
(2)经过20分,分针旋转了多少度?
解析:(1)它的旋转中心是钟表的轴心.
(2)分针匀速旋转一周需要60分,因此旋转20分,分针旋转的角度为 .
课堂小结
1.旋转中心在旋转过程中保持不动.
2.图形中每一点都绕着旋转中心旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段、角均相等.
3.旋转一定角度后能与自身重合.
4.旋转作图要找准原图形的位置、旋转中心、旋转角.
通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流。
第5章 轴对称与旋转
情景引入
如图 ,观察钟表的指针,电风扇的叶片,汽车的雨刮器在转动的过程中有什么共同的特征.
钟表的指针绕中间的固定点旋转,电风扇的叶片绕电机的轴旋转,汽车的雨刮器绕支点旋转.
获取新知
将一个平面图形F上的每一个点,绕这个平面内一个定点O旋转同一个角α,(即把图形F上每一个点与定点的连线绕定点O旋转α),得到图形F',如图,图形的这种变换叫做旋转.这个定点 O 叫旋转中心,角α叫做旋转角.
原位置的图形F叫做原像,新位置的图形F'叫做图形F在旋转下的像. 图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点.
旋转的决定因素:
旋转中心、旋转角度、旋转方向
旋转的定义
α
获取新知
如图,将三角形ABC按逆时针方向绕点O旋转60?得到三角形A'B'C',三角形ABC内的点P在这个旋转下的像是点P',则OA'与OA相等吗?∠POP'和∠AOA'相等吗?度数等于多少?
A'
B'
C'
A
B
C
O
.
.
P '
P
60?
由旋转的概念可得,OA与OA'相等.
由旋转的概念可得,∠POP'=60?=∠AOA'.
获取新知
一般地,旋转具有下述性质:
A'
B'
C'
A
B
C
O
.
.
P '
P
60?
一个图形和它经过旋转所得到的图形中, 对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的旋转角相等.
观察右图△ABC旋转到△A'B'C'位置时,形状和大小是否发生改变.
旋转不改变图形的形状和大小.
注意:
旋转角是指图形旋转的角度,而不是图形中的角度,对应角是指图形旋转前,旋转后能够互相重合的角。
例题讲解
【例】如图,将三角形ABC按逆时针方向旋转45?,得到三角形AB'C'.
(1)图中哪一点是旋转中心?
(2)∠B'CB和∠C'AC有何关系?它们的度数是多少?
(3)AB与AB',AC与AC'有何关系?
解:(1)点A是旋转中心.
(2)B与B',C与C'是对应点.因为两组对应点分别与旋转中心的连线所成的角相等,且等于旋转角,所以∠B'AB=∠C'AC=45?.
(3)因为对应点到旋转中心的距离相等,所以AB=AB',AC=AC'.
获取新知
平行四边形绕中心旋转
获取新知
1、相同:
B
A
C
O
2、不同:
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或逆时针
转动一定的角度
平移和旋转的异同:
都是一种运动;运动前后 不改变图形的形状和大小
获取新知
三角形绕点旋转加平移
例题讲解
随堂演练
【归纳总结】旋转性质的“两应用”
(1)应用一:判断线段或角是否相等.
①根据旋转角相等,对应点与旋转中心的连线相等可得角或线段相等;
②根据旋转后的图形与原来图形的形状、大小都相同可得图形的对应线段、对应角相等.
(2)应用二:计算图形的面积、线段的长度或角的大小.
随堂演练
获取新知
作旋转变换后的图形:
(1)先确定图形的关键点和(定点)旋转中心
(2)分别连接关键点和定点
(3)利用旋转性质作出关键点的对应点(根据旋转方向和旋转角度作出)
(3)按照原图形中的连接方法顺次连接各对应点,要注意旋转中心,旋转方向和旋转角
随堂演练
A
B'
OB'
A'B'
∠A'
∠B'
O
60
随堂演练
垂直
40
4.钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心.
(2)经过20分,分针旋转了多少度?
解析:(1)它的旋转中心是钟表的轴心.
(2)分针匀速旋转一周需要60分,因此旋转20分,分针旋转的角度为 .
课堂小结
1.旋转中心在旋转过程中保持不动.
2.图形中每一点都绕着旋转中心旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段、角均相等.
3.旋转一定角度后能与自身重合.
4.旋转作图要找准原图形的位置、旋转中心、旋转角.
通过本节课,你有什么收获?
你还存在哪些疑问,和同伴交流。
