沪科版九年级下册数学教案:24.1旋转
文档属性
| 名称 | 沪科版九年级下册数学教案:24.1旋转 |

|
|
| 格式 | zip | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览


文档简介
《旋转》教案
教学目标
1、了解旋转及其旋转中心和旋转角等相关概念.
2、理解旋转的基本性质并利用性质解决相关问题.
3、认识两个图形关于某一点或中心对称的本质:就是一个图形绕一点旋转180°而成.
4、利用中心对称的特征作出某一图形成中心对称的图形,确定对称中心的位置.
5、熟记中心对称图形的有关概念.
6、叙述并应用中心对称图形的基本性质.
教学重难点
重点:
1、旋转及对应点的有关概念及其应用.
2、中心对称的性质及初步应用.
3、中心对称图形的定义及其性质.
难点:
1、从活生生的数学中抽象出概念.
2、中心对称与旋转之间的关系.
3、中心对称图形的定义.
教学过程
一、认识旋转
(一)学生预习教师导学
观察下列图片:
(1)由平面图形转动而产生的奇妙图案;(2)汽车上的雨刮器.
●这些情景中的转动现象,有什么共同特征?
(二)学生探究教师引领
1、建立旋转的概念:
试一试,请同学们尝试用自己的语言来描述以下旋转.
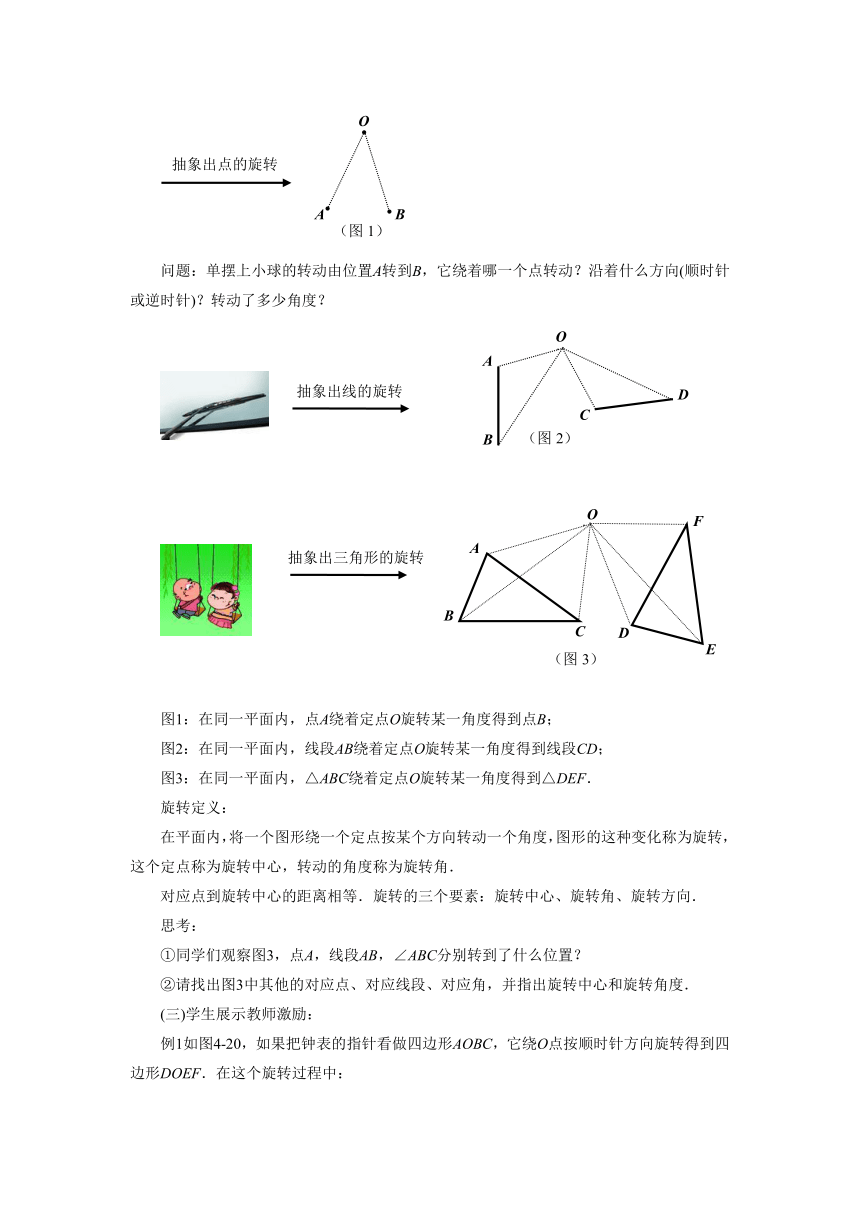
问题:单摆上小球的转动由位置A转到B,它绕着哪一个点转动?沿着什么方向(顺时针或逆时针)?转动了多少角度?
图1:在同一平面内,点A绕着定点O旋转某一角度得到点B;
图2:在同一平面内,线段AB绕着定点O旋转某一角度得到线段CD;
图3:在同一平面内,△ABC绕着定点O旋转某一角度得到△DEF.
旋转定义:
在平面内,将一个图形绕一个定点按某个方向转动一个角度,图形的这种变化称为旋转,这个定点称为旋转中心,转动的角度称为旋转角.
对应点到旋转中心的距离相等.旋转的三个要素:旋转中心、旋转角、旋转方向.
思考:
①同学们观察图3,点A,线段AB,∠ABC分别转到了什么位置?
②请找出图3中其他的对应点、对应线段、对应角,并指出旋转中心和旋转角度.
(三)学生展示教师激励:
例1如图4-20,如果把钟表的指针看做四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)写出它的旋转中心和旋转角;
(2)经过旋转,点A、C,B分别到达什么位置?
(3)AO与DO的长有什么关系?你还能在图4-20中找出相等的线段吗?说明理由;
(4)∠AOD与∠BOE有什么大小关系?你还能在图4-20中找出相等的角吗?说明理由.
解:(1)旋转中心是点O,旋转角是∠AOD.
(2)点A,C,B分别旋转到点D,F,E.
(3)AO=DO,BO=EO,AC=DF,CB=FE.
(4)∠AOD=∠BOE,∠A=∠D,∠C=∠F,∠B=∠E,∠AOB=∠DOE.
二、中心对称
观察图中三个图形旋转的角度,发现哪个图形与其他二个不同?
(一)合作交流解读探究:
教师指出在生活中有许许多多的图形都具有以上特征,在各个领域中都有广泛的应用.它都能给人以一种美的享受.本节我们就来研究这些图形的形成——中心对称.
探究:如图,旋转三角板,画关于点O对称的两个三角形;
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出△A'B'C';
第三步,移开三角板.
这样画出的△ABC与△A'B'C',关于点O对称.分别连接对应点AA'、BB'、CC'.点O在线段AA'上吗?如果在,在什么位置?△ABC与△A'B'C'有什么关系?
发现:我们可以发现:(1)点O是线段AA’的中点;(2)△ABC≌△A'B'C'.
上述发现可以证明如下.
(1)点A'是点A绕点O旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA',所以点O在线段AA'上,且OA=OA',即点O是线段AA'的中点.
(2)在△AOB与△A'OB'中,
OA=OA',OB=OB',∠AOB=∠A'OB',
∴△AOB≌△A'OB'.
∴AB=A'B'.
同理BC=B'C',AC=A'C'.
∴△ABC≌△A'B'C'.
探索:下图中△A'B'C'与△ABC关于点O是成中心对称的,你能从图中找到那些等量关系?
结论:(1)关于中心对称的两个图形中,对称点所连线段都经过对称中心,而且被对称中心所平分.
例1如图24-6,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A′B′C′D′.
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
作法
1.连接AO并延长到A′,使OA′=OA,得到点A的对应点A′.
2.同理,可作出点B,C,D的对应点B′,C′,D′.
3.顺次连接点A′,B′,C′,D′.
则四边形即为所作A′B′C′D′.
三、中心对称图形
如下图所示,在一个平行四边形纸板上,连结两条对角线,得到交点O,用图钉过点O将纸板固定在一张纸上,并描下此时四边形ABCD的轮廓.绕点O旋转平行四边形纸板,使得点A移动到点C的位置.
(1)此时的纸板与原来的位置是否重合?
(2)指出旋转中心,求出旋转角的度数.
(3)根据上面的过程,你能验证平行四边形的哪些性质?与同伴交流.
(学生动手做、讨论、总结)
[生1]把平行四边形纸板绕对角线的交点O旋转,使点A移动到点C的位置时,纸板与描下的轮廓重合.
平行四边形旋转的中心是对角线的交点O,由于点A和点C在一条直线上,所以旋转的角度为180°.
[师]这位同学分析得很正确:下面来看第(3)个问题,大家互相交流交流.
[生2]从刚才旋转的过程中,验证了平行四边形的对边相等,对角相等,对角线互相平分等性质.
[师]很好,我们来看(演示刚才学生旋转的过程),这个平行四边形绕它的对角线的交点O旋转180°,它与原图重合,我们把这样的图形,称为中心对称图形.
[师]我们再来看这根木条(出示教具),它绕着这一点(指出木条的中点)旋转180°时,也和原图重合.即与它本身重合,这样的图形叫中心对称图形.
大家来总结归纳:什么是中心对称图形?
[生]把一个图形绕它的某个点旋转180°,如果旋转后的图形与原来的图形重合,那么这个图形叫做中心对称图形.
[师]很好,在平面内,一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形(centralsymmetryfigure).这个点叫做它的对称中心.
想一想,平行四边形的对称中心是什么?
[生]平行四边形的对称中心是对角线的交点.
[师]对,大家再想一想:我们学过的哪些图形是中心对称图形.
[生]线段、平行四边形、矩形、菱形、正方形.
[师]很好,它们的对称中心各是什么?
[生]线段的对称中心是线段的中点.平行四边形的对称中心是对角线的交点,因为矩形、菱形、正方形是特殊的平行四边形,所以它们的对称中心都是对角线的交点.
[师]这位同学回答得真棒.
假设点A是某个中心对称图形上的一点,绕O点旋转180°后,它变成了点C,点A和点C就是一对对应点,而且O是AC的中点.(如图)
再看平行四边形是中心对称图形,点B绕O点旋转180°后,它与点D重合,点B和点D就是一对对应点,从平行四边形的性质也可知:O是BD的中点.
由此大家能否总结出中心对称图形的性质吗?
[生]中心对称图形上的每一对对应点所连成的线段的中点都是对称中心.
[师]同学们总结得很好,这就是中心对称图形的性质.
中心对称图形上的每一对对应点所连成的线段都被对称中心平分.
中心对称图形在日常生活和生产中有广泛的应用,请你举出所看到的中心对称图形的实例.
[生甲]家庭装饰中的各种图案、竹签做的玩具小飞机、纸做的小风车.
[生乙]飞机的双叶螺丝桨、风车的风轮.
[生丙]水泵叶轮……
[师]很好,大家举出这么多中心对称图形的例子.你能说说中心对称图形在欣赏和实用方面的价值吗?(出示一些中心对称图形的图片).
[生1]中心对称图形的形状匀称、美观,所以在很多建筑物和工艺品上常用这种图形作装饰图案.
[生2]由于中心对称图形绕中心旋转180°,后与原来的图形重合.所以具有中心对称图形的物体,在平面内能绕对称中心平稳地旋转.这种特性在生活和生产中都有应用.
[师]同学们回答得真棒.下面大家拿出扑克牌,看看这些牌的牌面哪些是中心对称图形?
[生1]红桃2、方块2、黑桃2、黑桃10、方块J、梅花10、方块K、黑桃4.
[生2]红桃4、红桃K、梅花Q.
[生3]方块中除7不是,其余的都是中心对称图形.
[师]很好,从大家回答中知道同学们基本掌握了中心对称图形的概念.
下面大家来“想一想”.
除了平行四边形,你还能找到哪些多边形是中心对称图形?
[生1]正六边形、正八边形、正十边形.
[生2]这样的多边形很多,在正多边形中,只要边数为偶数,那它就是中心对称图形.
[师]很好,下面我们来做练习,以巩固中心对称图形的定义及性质.
四、旋转的基本性质:
一般地,我们可以得到:一个图形和它经过旋转所得到的图形中,
(1)旋转不改变图形的大小,对应边相等,对应角相等.
(2)图形上的每一点都绕旋转中心沿相同方向转动了旋转角.
(3)任意一对对应点与旋转中心的连线所成的角度都等于旋转角.
(4)成中心对称和中心对称图形的有关概念和它的基本性质.能判定一个图形是否是中心对称图形.
抽象出点的旋转
A
B
(图1)
O
抽象出三角形的旋转
·
O
A
B
CO
F
D
E
(图3)
·
O
A
B
C
D
(图2)
抽象出线的旋转
教学目标
1、了解旋转及其旋转中心和旋转角等相关概念.
2、理解旋转的基本性质并利用性质解决相关问题.
3、认识两个图形关于某一点或中心对称的本质:就是一个图形绕一点旋转180°而成.
4、利用中心对称的特征作出某一图形成中心对称的图形,确定对称中心的位置.
5、熟记中心对称图形的有关概念.
6、叙述并应用中心对称图形的基本性质.
教学重难点
重点:
1、旋转及对应点的有关概念及其应用.
2、中心对称的性质及初步应用.
3、中心对称图形的定义及其性质.
难点:
1、从活生生的数学中抽象出概念.
2、中心对称与旋转之间的关系.
3、中心对称图形的定义.
教学过程
一、认识旋转
(一)学生预习教师导学
观察下列图片:
(1)由平面图形转动而产生的奇妙图案;(2)汽车上的雨刮器.
●这些情景中的转动现象,有什么共同特征?
(二)学生探究教师引领
1、建立旋转的概念:
试一试,请同学们尝试用自己的语言来描述以下旋转.
问题:单摆上小球的转动由位置A转到B,它绕着哪一个点转动?沿着什么方向(顺时针或逆时针)?转动了多少角度?
图1:在同一平面内,点A绕着定点O旋转某一角度得到点B;
图2:在同一平面内,线段AB绕着定点O旋转某一角度得到线段CD;
图3:在同一平面内,△ABC绕着定点O旋转某一角度得到△DEF.
旋转定义:
在平面内,将一个图形绕一个定点按某个方向转动一个角度,图形的这种变化称为旋转,这个定点称为旋转中心,转动的角度称为旋转角.
对应点到旋转中心的距离相等.旋转的三个要素:旋转中心、旋转角、旋转方向.
思考:
①同学们观察图3,点A,线段AB,∠ABC分别转到了什么位置?
②请找出图3中其他的对应点、对应线段、对应角,并指出旋转中心和旋转角度.
(三)学生展示教师激励:
例1如图4-20,如果把钟表的指针看做四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)写出它的旋转中心和旋转角;
(2)经过旋转,点A、C,B分别到达什么位置?
(3)AO与DO的长有什么关系?你还能在图4-20中找出相等的线段吗?说明理由;
(4)∠AOD与∠BOE有什么大小关系?你还能在图4-20中找出相等的角吗?说明理由.
解:(1)旋转中心是点O,旋转角是∠AOD.
(2)点A,C,B分别旋转到点D,F,E.
(3)AO=DO,BO=EO,AC=DF,CB=FE.
(4)∠AOD=∠BOE,∠A=∠D,∠C=∠F,∠B=∠E,∠AOB=∠DOE.
二、中心对称
观察图中三个图形旋转的角度,发现哪个图形与其他二个不同?
(一)合作交流解读探究:
教师指出在生活中有许许多多的图形都具有以上特征,在各个领域中都有广泛的应用.它都能给人以一种美的享受.本节我们就来研究这些图形的形成——中心对称.
探究:如图,旋转三角板,画关于点O对称的两个三角形;
第一步,画出△ABC;
第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出△A'B'C';
第三步,移开三角板.
这样画出的△ABC与△A'B'C',关于点O对称.分别连接对应点AA'、BB'、CC'.点O在线段AA'上吗?如果在,在什么位置?△ABC与△A'B'C'有什么关系?
发现:我们可以发现:(1)点O是线段AA’的中点;(2)△ABC≌△A'B'C'.
上述发现可以证明如下.
(1)点A'是点A绕点O旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA',所以点O在线段AA'上,且OA=OA',即点O是线段AA'的中点.
(2)在△AOB与△A'OB'中,
OA=OA',OB=OB',∠AOB=∠A'OB',
∴△AOB≌△A'OB'.
∴AB=A'B'.
同理BC=B'C',AC=A'C'.
∴△ABC≌△A'B'C'.
探索:下图中△A'B'C'与△ABC关于点O是成中心对称的,你能从图中找到那些等量关系?
结论:(1)关于中心对称的两个图形中,对称点所连线段都经过对称中心,而且被对称中心所平分.
例1如图24-6,已知四边形ABCD和点O,试画出四边形ABCD关于点O成中心对称的图形A′B′C′D′.
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
作法
1.连接AO并延长到A′,使OA′=OA,得到点A的对应点A′.
2.同理,可作出点B,C,D的对应点B′,C′,D′.
3.顺次连接点A′,B′,C′,D′.
则四边形即为所作A′B′C′D′.
三、中心对称图形
如下图所示,在一个平行四边形纸板上,连结两条对角线,得到交点O,用图钉过点O将纸板固定在一张纸上,并描下此时四边形ABCD的轮廓.绕点O旋转平行四边形纸板,使得点A移动到点C的位置.
(1)此时的纸板与原来的位置是否重合?
(2)指出旋转中心,求出旋转角的度数.
(3)根据上面的过程,你能验证平行四边形的哪些性质?与同伴交流.
(学生动手做、讨论、总结)
[生1]把平行四边形纸板绕对角线的交点O旋转,使点A移动到点C的位置时,纸板与描下的轮廓重合.
平行四边形旋转的中心是对角线的交点O,由于点A和点C在一条直线上,所以旋转的角度为180°.
[师]这位同学分析得很正确:下面来看第(3)个问题,大家互相交流交流.
[生2]从刚才旋转的过程中,验证了平行四边形的对边相等,对角相等,对角线互相平分等性质.
[师]很好,我们来看(演示刚才学生旋转的过程),这个平行四边形绕它的对角线的交点O旋转180°,它与原图重合,我们把这样的图形,称为中心对称图形.
[师]我们再来看这根木条(出示教具),它绕着这一点(指出木条的中点)旋转180°时,也和原图重合.即与它本身重合,这样的图形叫中心对称图形.
大家来总结归纳:什么是中心对称图形?
[生]把一个图形绕它的某个点旋转180°,如果旋转后的图形与原来的图形重合,那么这个图形叫做中心对称图形.
[师]很好,在平面内,一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形(centralsymmetryfigure).这个点叫做它的对称中心.
想一想,平行四边形的对称中心是什么?
[生]平行四边形的对称中心是对角线的交点.
[师]对,大家再想一想:我们学过的哪些图形是中心对称图形.
[生]线段、平行四边形、矩形、菱形、正方形.
[师]很好,它们的对称中心各是什么?
[生]线段的对称中心是线段的中点.平行四边形的对称中心是对角线的交点,因为矩形、菱形、正方形是特殊的平行四边形,所以它们的对称中心都是对角线的交点.
[师]这位同学回答得真棒.
假设点A是某个中心对称图形上的一点,绕O点旋转180°后,它变成了点C,点A和点C就是一对对应点,而且O是AC的中点.(如图)
再看平行四边形是中心对称图形,点B绕O点旋转180°后,它与点D重合,点B和点D就是一对对应点,从平行四边形的性质也可知:O是BD的中点.
由此大家能否总结出中心对称图形的性质吗?
[生]中心对称图形上的每一对对应点所连成的线段的中点都是对称中心.
[师]同学们总结得很好,这就是中心对称图形的性质.
中心对称图形上的每一对对应点所连成的线段都被对称中心平分.
中心对称图形在日常生活和生产中有广泛的应用,请你举出所看到的中心对称图形的实例.
[生甲]家庭装饰中的各种图案、竹签做的玩具小飞机、纸做的小风车.
[生乙]飞机的双叶螺丝桨、风车的风轮.
[生丙]水泵叶轮……
[师]很好,大家举出这么多中心对称图形的例子.你能说说中心对称图形在欣赏和实用方面的价值吗?(出示一些中心对称图形的图片).
[生1]中心对称图形的形状匀称、美观,所以在很多建筑物和工艺品上常用这种图形作装饰图案.
[生2]由于中心对称图形绕中心旋转180°,后与原来的图形重合.所以具有中心对称图形的物体,在平面内能绕对称中心平稳地旋转.这种特性在生活和生产中都有应用.
[师]同学们回答得真棒.下面大家拿出扑克牌,看看这些牌的牌面哪些是中心对称图形?
[生1]红桃2、方块2、黑桃2、黑桃10、方块J、梅花10、方块K、黑桃4.
[生2]红桃4、红桃K、梅花Q.
[生3]方块中除7不是,其余的都是中心对称图形.
[师]很好,从大家回答中知道同学们基本掌握了中心对称图形的概念.
下面大家来“想一想”.
除了平行四边形,你还能找到哪些多边形是中心对称图形?
[生1]正六边形、正八边形、正十边形.
[生2]这样的多边形很多,在正多边形中,只要边数为偶数,那它就是中心对称图形.
[师]很好,下面我们来做练习,以巩固中心对称图形的定义及性质.
四、旋转的基本性质:
一般地,我们可以得到:一个图形和它经过旋转所得到的图形中,
(1)旋转不改变图形的大小,对应边相等,对应角相等.
(2)图形上的每一点都绕旋转中心沿相同方向转动了旋转角.
(3)任意一对对应点与旋转中心的连线所成的角度都等于旋转角.
(4)成中心对称和中心对称图形的有关概念和它的基本性质.能判定一个图形是否是中心对称图形.
抽象出点的旋转
A
B
(图1)
O
抽象出三角形的旋转
·
O
A
B
CO
F
D
E
(图3)
·
O
A
B
C
D
(图2)
抽象出线的旋转
