高中数学人教B版必修二第二章2.3.1 圆的标准方程课件4(17张PPT)
文档属性
| 名称 | 高中数学人教B版必修二第二章2.3.1 圆的标准方程课件4(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 433.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
圆的世界
1.两点间距离公式
已知P1(x1,y1),
P2(x2,y2),则
一
知识点复习
3、确定圆有需要几个要素?
圆心--确定圆的位置(定位)
半径--确定圆的大小(定形)
平面内到定点距离等于定长的点的轨迹(集合)是圆.
定点是圆心,定长是半径
2、圆的定义?
4、在直角坐标系中如何写出圆的方程?
?
O
x
y
C(a,b)
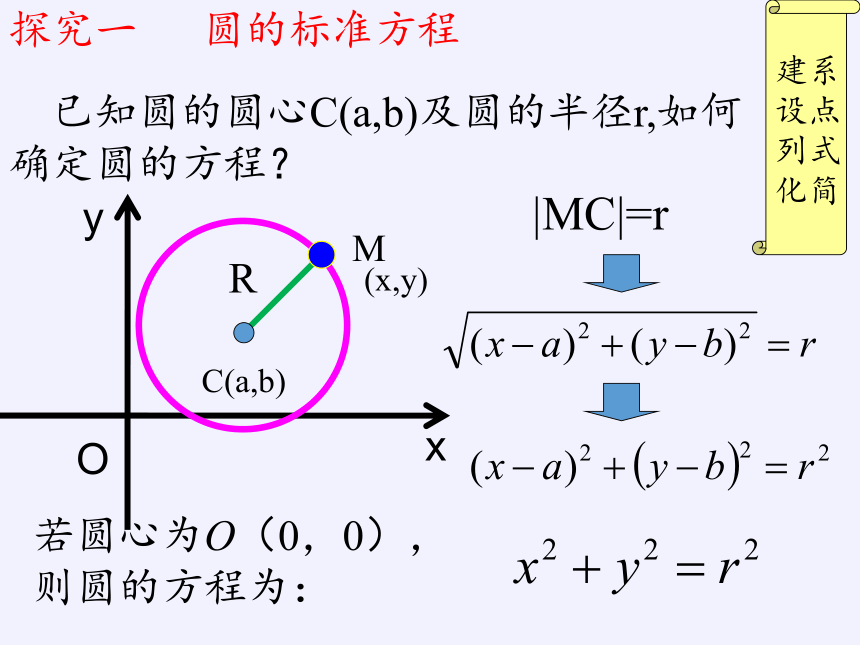
已知圆的圆心C(a,b)及圆的半径r,如何确定圆的方程?
M
探究一
圆的标准方程
R
|MC|=r
若圆心为O(0,0),则圆的方程为:
(x,y)
建系
设点
列式
化简
例题1
求圆的标准方程
(1)圆心在点C(-2,1),并过点A(2,-2)
解:因为圆心为C(-2,1),所以可设圆的标准方程为
只需明确:圆心和半径即可
所求圆的标准方程为
(2)圆心在点C(1,3),并与直线3x-4y-6=0相切
解:因为圆心是C(1,3),所以可设所求圆的标准方程为
因为直线为圆的切线,所有圆心C(1,3)到直线3x-4y-6=0的距离等于半径,根据点到直线距离公式,有
所以圆的标准方程为
(3)过点(0,1)和点(2,1),半径为
解:设圆的标准方程为
把点分别代入圆的标准方程,得:
所以圆的
标准方程为
解得
怎样判断点
在圆
内呢?圆上?还是在圆外呢?
x
y
o
探究二
点和圆的位置关系
(x0-a)2+(y0-b)2(x0-a)2+(y0-b)2=r2时,点M在圆C上
(x0-a)2+(y0-b)2>r2时,点M在圆C外
M3
M1
M2
A在圆外
B在圆上
C在圆内
D在圆上或圆外
m
1
点P(
,4)与圆x2+y2=16的位置关系
(
)
练一练
真棒!
圆心:两条直线的交点
半径:圆心到圆上一点
x
y
O
C
A(6,0)
B(1,5)
弦AB的垂直平分线
例2
求过点A(6,0)和B(1,5),且圆心在直线
L:2x-7y+8=0上的圆的方程.
m
L
几何方法
法一
圆经过A(6,0),B(1,5)
法二:设圆C的方程为
又圆心在直线L:2x-7y+8=0上
待定系数法
例2
求过点A(6,0)和B(1,5),且圆心在直线
L:2x-7y+8=0上的圆的方程.
例3
赵州桥的跨度是37.02米,圆拱高约7.2米,求这座圆拱桥的拱圆方程(精确到0.01m)
(0,b)
代入点B,C坐标即可:
解得
拱圆方程近似为
解:以AB中点为原点如图建系,可知圆心坐标为M(0,b),所以可设圆的标准方程为:
M
A
0
B
C
(0,7.2)
(18.51,0)
x
y
(-18.51,0)
圆心C(a,b),半径r
特别地若圆心为O(0,0),则圆的标准方程为:
课堂小结:
一、
二、点与圆的位置关系:
三、求圆的标准方程的方法:
2
几何方法:数形结合(圆心一定在弦的中垂线上)
1
代数方法:待定系数法求
今天有什
么收获?
圆的标准方程
(1)点P在圆上
(2)点P在圆内
(3)点P在圆外
作业布置
习题A组1、2题
习题B组1、2题
你对本节课哪个知识点
还有些疑惑???
课后思考题
将标准方程展开,是一个什么形式?
它有什么特点?
谢
谢
圆的世界
1.两点间距离公式
已知P1(x1,y1),
P2(x2,y2),则
一
知识点复习
3、确定圆有需要几个要素?
圆心--确定圆的位置(定位)
半径--确定圆的大小(定形)
平面内到定点距离等于定长的点的轨迹(集合)是圆.
定点是圆心,定长是半径
2、圆的定义?
4、在直角坐标系中如何写出圆的方程?
?
O
x
y
C(a,b)
已知圆的圆心C(a,b)及圆的半径r,如何确定圆的方程?
M
探究一
圆的标准方程
R
|MC|=r
若圆心为O(0,0),则圆的方程为:
(x,y)
建系
设点
列式
化简
例题1
求圆的标准方程
(1)圆心在点C(-2,1),并过点A(2,-2)
解:因为圆心为C(-2,1),所以可设圆的标准方程为
只需明确:圆心和半径即可
所求圆的标准方程为
(2)圆心在点C(1,3),并与直线3x-4y-6=0相切
解:因为圆心是C(1,3),所以可设所求圆的标准方程为
因为直线为圆的切线,所有圆心C(1,3)到直线3x-4y-6=0的距离等于半径,根据点到直线距离公式,有
所以圆的标准方程为
(3)过点(0,1)和点(2,1),半径为
解:设圆的标准方程为
把点分别代入圆的标准方程,得:
所以圆的
标准方程为
解得
怎样判断点
在圆
内呢?圆上?还是在圆外呢?
x
y
o
探究二
点和圆的位置关系
(x0-a)2+(y0-b)2
(x0-a)2+(y0-b)2>r2时,点M在圆C外
M3
M1
M2
A在圆外
B在圆上
C在圆内
D在圆上或圆外
m
1
点P(
,4)与圆x2+y2=16的位置关系
(
)
练一练
真棒!
圆心:两条直线的交点
半径:圆心到圆上一点
x
y
O
C
A(6,0)
B(1,5)
弦AB的垂直平分线
例2
求过点A(6,0)和B(1,5),且圆心在直线
L:2x-7y+8=0上的圆的方程.
m
L
几何方法
法一
圆经过A(6,0),B(1,5)
法二:设圆C的方程为
又圆心在直线L:2x-7y+8=0上
待定系数法
例2
求过点A(6,0)和B(1,5),且圆心在直线
L:2x-7y+8=0上的圆的方程.
例3
赵州桥的跨度是37.02米,圆拱高约7.2米,求这座圆拱桥的拱圆方程(精确到0.01m)
(0,b)
代入点B,C坐标即可:
解得
拱圆方程近似为
解:以AB中点为原点如图建系,可知圆心坐标为M(0,b),所以可设圆的标准方程为:
M
A
0
B
C
(0,7.2)
(18.51,0)
x
y
(-18.51,0)
圆心C(a,b),半径r
特别地若圆心为O(0,0),则圆的标准方程为:
课堂小结:
一、
二、点与圆的位置关系:
三、求圆的标准方程的方法:
2
几何方法:数形结合(圆心一定在弦的中垂线上)
1
代数方法:待定系数法求
今天有什
么收获?
圆的标准方程
(1)点P在圆上
(2)点P在圆内
(3)点P在圆外
作业布置
习题A组1、2题
习题B组1、2题
你对本节课哪个知识点
还有些疑惑???
课后思考题
将标准方程展开,是一个什么形式?
它有什么特点?
谢
谢
