人教版八年级上册数学课件:15.2.3整数指数幂(共36张ppt)
文档属性
| 名称 | 人教版八年级上册数学课件:15.2.3整数指数幂(共36张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 959.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:27:36 | ||
图片预览








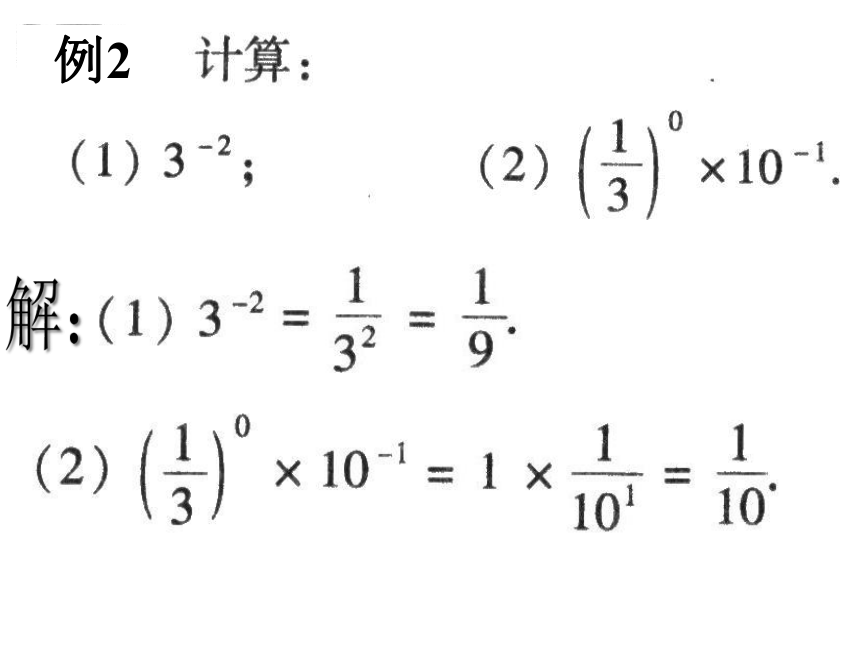
文档简介
(共36张PPT)
15.2.3整数指数幂
1.零指数幂与
负整指数幂
2.
科学记数法
学习目标
1.理解零指数幂与负指数幂的性质,能够熟练地应用其公式进行计算。
2.理解科学记数法的意义,能够用科学记数法表示绝对值小于1的非零数,会把一个用科学记数法表示的数写成小数的形式。
3.通过独立思考,小组合作,体会到从特殊到一般的数学研究方法。
重点:理解和应用零指数幂和负指数幂的性质。
难点:理解和应用负指数幂的性质。
回
顾
【同底数幂相除的法则】
一般地,设m、n为正整数,m>n,a≠0,有
不
忘
老
朋
友
>
思考:在§14.1中介绍同底数幂的除法公式am÷an=am-n时,有一个附加条件:m>n,即被除数的指数大于除数的指数.当被除数的指数不大于除数的指数,即m=n或m<n时,情况怎样呢?
讲解零指数幂的有关知识
探索新知1
1
1
……
……
1
结论:
……
任何不等于零的数的零次幂都等于1.
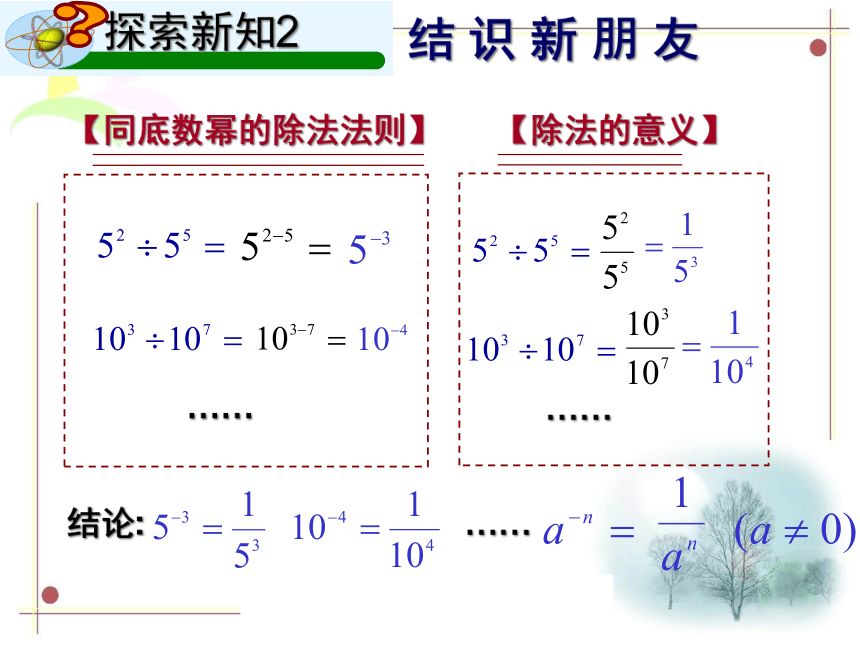
【同底数幂的除法法则】
【除法的意义】
结
识
新
朋
友
做一做
初试锋芒
判断
×
√
√
√
√
应用零指数幂性质的条件:
(1)验证底数是否为零;
(2)若底数不为零,
可以套用零指数幂的性质;
若底数为零,则无意义.
例1
计算
探索新知2
……
……
结论:
……
【同底数幂的除法法则】
【除法的意义】
结
识
新
朋
友
任何不等于零的数的负整数次幂等于它的正整数次幂的倒数.
知识归纳
负整指数幂成立的条件是底数不为零,即
解:
例2
(2)
25
000
=
2.5
×
10
000
=
2.5
×
104
(3)
5
034
=
5.034
×
1
000
=
5.034
×
103
(1)
400
000
=
4
×
100
000
=
4
×
105
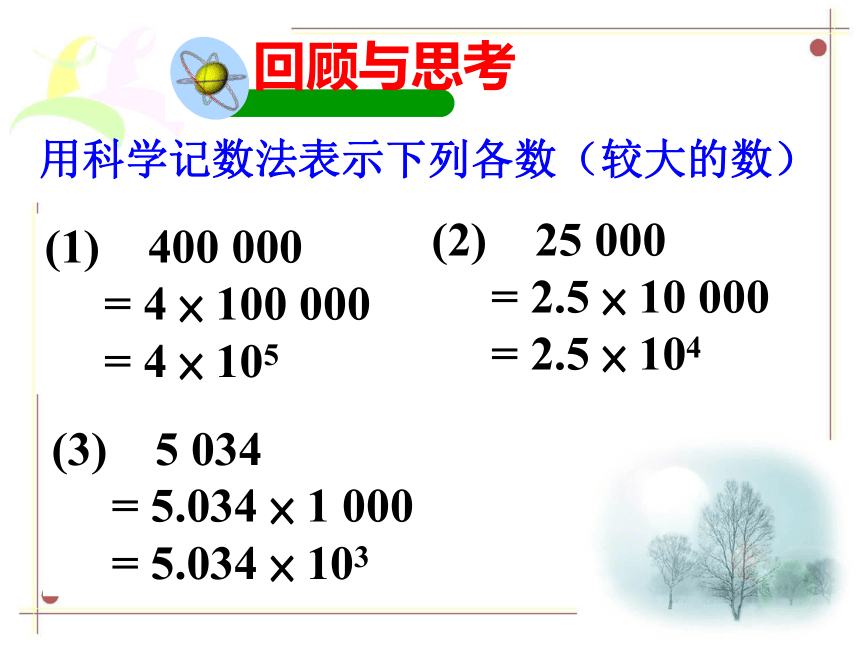
回顾与思考
用科学记数法表示下列各数(较大的数)
(1)
400
000
=
4
×
100
000
=
4
×
105
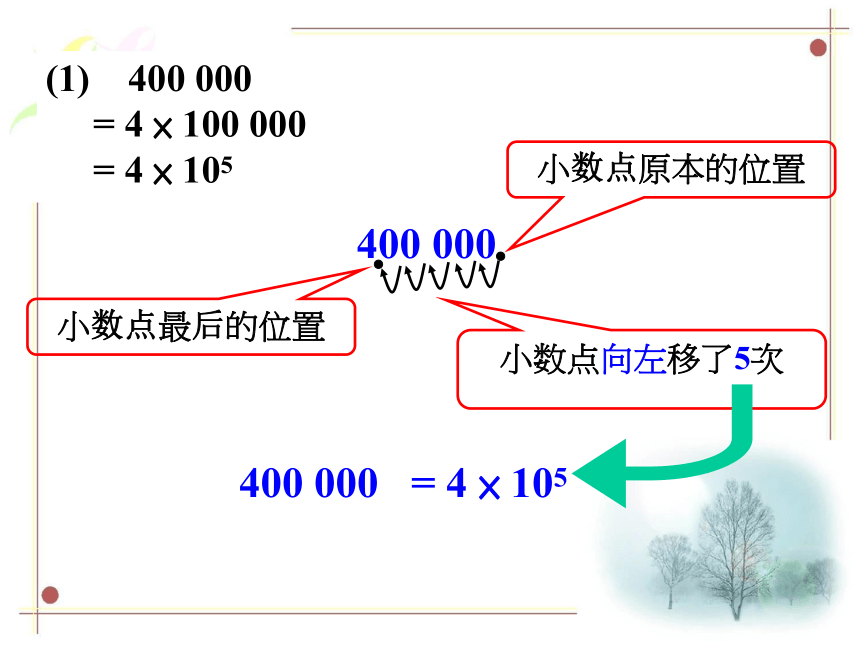
400
000
400
000
=
4
×
105
小数点原本的位置
小数点最后的位置
小数点向左移了5次
(2)
25
000
=
2.5
×
10
000
=
2.5
×
104
25
000
25
000
=
2.5
×
104
小数点原本的位置
小数点最后的位置
小数点向左移了4次
(3)
5
034
=
5.034
×
1
000
=
5.034
×
103
5
034
5
034
=
5.034
×
103
小数点原本的位置
小数点最后的位置
小数点向左移了3次
如何用科学记数法表示绝对值小于1的数?
探索新知3
0.1
=
0.01
=
0.001
=
10-1
10-2
10-3
方法分析
(4)
0.005
=
5
×
0.001
=
5
×
10-3
(5)
0.020
4
=
2.04
×
0.01
=
2.04
×
10-2
(6)
0.000
36
=
3.6
×
0.000
1
=
3.6
×
10-4
用科学记数法表示下列各数:
(4)
0.005
=
5
×
0.001
=
5
×
10-3
0.005
0.005
=
5
×
10-3
小数点原本的位置
小数点最后的位置
小数点向右移了3次
(5)
0.020
4
=
2.04
×
0.01
=
2.04
×
10-2
0.02
04
0.020
4
=
2.04
×
10-2
小数点原本的位置
小数点最后的位置
小数点向右移了2次
(6)
0.000
36
=
3.6
×
0.000
1
=
3.6
×
10-4
0.000
36
0.000
36
=
3.6
×
10-4
小数点原本的位置
小数点最后的位置
小数点向右移了4次
用科学记数法表示下列各数:
1)
0.0005
2)
-0.0204
3)
0.0000314
例3
(1)
0.005
=
5
×
0.001
=
5
×
10-3
(2)
-0.020
4
=
2.04
×
0.01
=
2.04
×
10-2
(3)
0.000
314
=
3.14×
0.000
1
=
3.14
×
10-4
用科学记数法表示下列各数:
例
4
用小数表示下列各数:
解:
预习反馈
1.优秀小组:
优秀个人:
2.存在的问题:
(1)
(2)
(3)
合作探究
内容:
1.
学习中遇到的疑问
2.导学案“质疑探究”部分的问题
要求:
(1)人人参与,热烈讨论,大声表达自己的思想.
(2)组长控制好讨论节奏,先一对一分层讨论,再小组内集中讨论.
(3)没解决的问题组长记录好,准备质疑.
展示内容
展示小组
基础知识探究点1
(口头展示)
2、组
基础知识探究点2
(口头展示)
5
知识综合探究点一
1题
4
知识综合探究点一
2题
8
知识综合探究点一
3题
6
知识综合探究点一
4题
9
高效展示
要求
⑴口头展示,声音洪亮、清楚;书面展示要分层次、要点化,书写要认真、
规范.
⑵非展示同学巩固基础知识、整理落实学案,做好拓展.不浪费一分钟,小组长做好安排和检查.
点评内容
点评小组
知识综合应用探究点1
7组
知识综合应用探究点2
1组
知识综合应用探究点3
3组
要求:
⑴先点评对错,再点评思路方法,应该注意的问题,力争进行必要的变形拓展.
⑵其他同学认真倾听、积极思考、记好笔记、大胆质疑.
精彩点评
www.czsx.com.cn
1.计算下列各式,并把结果化为只含有正整数指数幂的形式:
(1)
(a-3)2(ab2)-3
(2)
(2mn2)-2(m-2n-1)-3
反馈练习
2
1
1
)
3
2
).(
3
(
)
3
).(
2
(
2
).
1
(
-
-
-
-
对于(1)(2)你有什么发现了吗?
对于(3)你作怎样的大胆猜想?
计算
当堂检测
要求:学生独立完成
时间:2分钟
当堂练习
1.用小数或分数表示下列各数.
拓展练习
如果代数式
有意义,
求x的取值范围.
拓展练习
课堂小结:
任何不等于零的数的零次幂都等于1.
今天我知道了……学会了……我能……
任何不等于零的数的负整数次幂等于它的正整数次幂的倒数.
再见!
15.2.3整数指数幂
1.零指数幂与
负整指数幂
2.
科学记数法
学习目标
1.理解零指数幂与负指数幂的性质,能够熟练地应用其公式进行计算。
2.理解科学记数法的意义,能够用科学记数法表示绝对值小于1的非零数,会把一个用科学记数法表示的数写成小数的形式。
3.通过独立思考,小组合作,体会到从特殊到一般的数学研究方法。
重点:理解和应用零指数幂和负指数幂的性质。
难点:理解和应用负指数幂的性质。
回
顾
【同底数幂相除的法则】
一般地,设m、n为正整数,m>n,a≠0,有
不
忘
老
朋
友
>
思考:在§14.1中介绍同底数幂的除法公式am÷an=am-n时,有一个附加条件:m>n,即被除数的指数大于除数的指数.当被除数的指数不大于除数的指数,即m=n或m<n时,情况怎样呢?
讲解零指数幂的有关知识
探索新知1
1
1
……
……
1
结论:
……
任何不等于零的数的零次幂都等于1.
【同底数幂的除法法则】
【除法的意义】
结
识
新
朋
友
做一做
初试锋芒
判断
×
√
√
√
√
应用零指数幂性质的条件:
(1)验证底数是否为零;
(2)若底数不为零,
可以套用零指数幂的性质;
若底数为零,则无意义.
例1
计算
探索新知2
……
……
结论:
……
【同底数幂的除法法则】
【除法的意义】
结
识
新
朋
友
任何不等于零的数的负整数次幂等于它的正整数次幂的倒数.
知识归纳
负整指数幂成立的条件是底数不为零,即
解:
例2
(2)
25
000
=
2.5
×
10
000
=
2.5
×
104
(3)
5
034
=
5.034
×
1
000
=
5.034
×
103
(1)
400
000
=
4
×
100
000
=
4
×
105
回顾与思考
用科学记数法表示下列各数(较大的数)
(1)
400
000
=
4
×
100
000
=
4
×
105
400
000
400
000
=
4
×
105
小数点原本的位置
小数点最后的位置
小数点向左移了5次
(2)
25
000
=
2.5
×
10
000
=
2.5
×
104
25
000
25
000
=
2.5
×
104
小数点原本的位置
小数点最后的位置
小数点向左移了4次
(3)
5
034
=
5.034
×
1
000
=
5.034
×
103
5
034
5
034
=
5.034
×
103
小数点原本的位置
小数点最后的位置
小数点向左移了3次
如何用科学记数法表示绝对值小于1的数?
探索新知3
0.1
=
0.01
=
0.001
=
10-1
10-2
10-3
方法分析
(4)
0.005
=
5
×
0.001
=
5
×
10-3
(5)
0.020
4
=
2.04
×
0.01
=
2.04
×
10-2
(6)
0.000
36
=
3.6
×
0.000
1
=
3.6
×
10-4
用科学记数法表示下列各数:
(4)
0.005
=
5
×
0.001
=
5
×
10-3
0.005
0.005
=
5
×
10-3
小数点原本的位置
小数点最后的位置
小数点向右移了3次
(5)
0.020
4
=
2.04
×
0.01
=
2.04
×
10-2
0.02
04
0.020
4
=
2.04
×
10-2
小数点原本的位置
小数点最后的位置
小数点向右移了2次
(6)
0.000
36
=
3.6
×
0.000
1
=
3.6
×
10-4
0.000
36
0.000
36
=
3.6
×
10-4
小数点原本的位置
小数点最后的位置
小数点向右移了4次
用科学记数法表示下列各数:
1)
0.0005
2)
-0.0204
3)
0.0000314
例3
(1)
0.005
=
5
×
0.001
=
5
×
10-3
(2)
-0.020
4
=
2.04
×
0.01
=
2.04
×
10-2
(3)
0.000
314
=
3.14×
0.000
1
=
3.14
×
10-4
用科学记数法表示下列各数:
例
4
用小数表示下列各数:
解:
预习反馈
1.优秀小组:
优秀个人:
2.存在的问题:
(1)
(2)
(3)
合作探究
内容:
1.
学习中遇到的疑问
2.导学案“质疑探究”部分的问题
要求:
(1)人人参与,热烈讨论,大声表达自己的思想.
(2)组长控制好讨论节奏,先一对一分层讨论,再小组内集中讨论.
(3)没解决的问题组长记录好,准备质疑.
展示内容
展示小组
基础知识探究点1
(口头展示)
2、组
基础知识探究点2
(口头展示)
5
知识综合探究点一
1题
4
知识综合探究点一
2题
8
知识综合探究点一
3题
6
知识综合探究点一
4题
9
高效展示
要求
⑴口头展示,声音洪亮、清楚;书面展示要分层次、要点化,书写要认真、
规范.
⑵非展示同学巩固基础知识、整理落实学案,做好拓展.不浪费一分钟,小组长做好安排和检查.
点评内容
点评小组
知识综合应用探究点1
7组
知识综合应用探究点2
1组
知识综合应用探究点3
3组
要求:
⑴先点评对错,再点评思路方法,应该注意的问题,力争进行必要的变形拓展.
⑵其他同学认真倾听、积极思考、记好笔记、大胆质疑.
精彩点评
www.czsx.com.cn
1.计算下列各式,并把结果化为只含有正整数指数幂的形式:
(1)
(a-3)2(ab2)-3
(2)
(2mn2)-2(m-2n-1)-3
反馈练习
2
1
1
)
3
2
).(
3
(
)
3
).(
2
(
2
).
1
(
-
-
-
-
对于(1)(2)你有什么发现了吗?
对于(3)你作怎样的大胆猜想?
计算
当堂检测
要求:学生独立完成
时间:2分钟
当堂练习
1.用小数或分数表示下列各数.
拓展练习
如果代数式
有意义,
求x的取值范围.
拓展练习
课堂小结:
任何不等于零的数的零次幂都等于1.
今天我知道了……学会了……我能……
任何不等于零的数的负整数次幂等于它的正整数次幂的倒数.
再见!
