24.1 放缩与相似形 教案
图片预览

文档简介
§24.1
放缩与相似形
教学目标:
1.能用图形放缩运动的观点认识相似形的意义.
2.知道相似形的概念,理解相似多边形的对应角、对应边的含义.
3.通过对进行放缩运动的图形进行度量分析,认识放缩运动中的不变量,知道相似多边形的特征以及相似形与全等形的关系.
教学重点和难点:
相似形的意义及性质
教学过程:
教师活动
学生活动
教学设计意图
引入
问1.证明三角形全等有哪些方法?
问2.能用角角角证明两个三角形全等吗?如果不能,请举出反例
问3.
这两个等边三角形有什么特点?
问4.
以上四组图形用什么共性?
问5.
我们给具备这种特性的两个图形一个什么名称呢?
学习新知
1、相似形的定义
问6:你能说出相似形的概念吗?
(教师要特别强调形状相同即可,大小可以相同也可以不相同)
问7:
两个全等形是相似形吗?
2.
观察几何画板动态演示,探索相似多边形性质
观察1
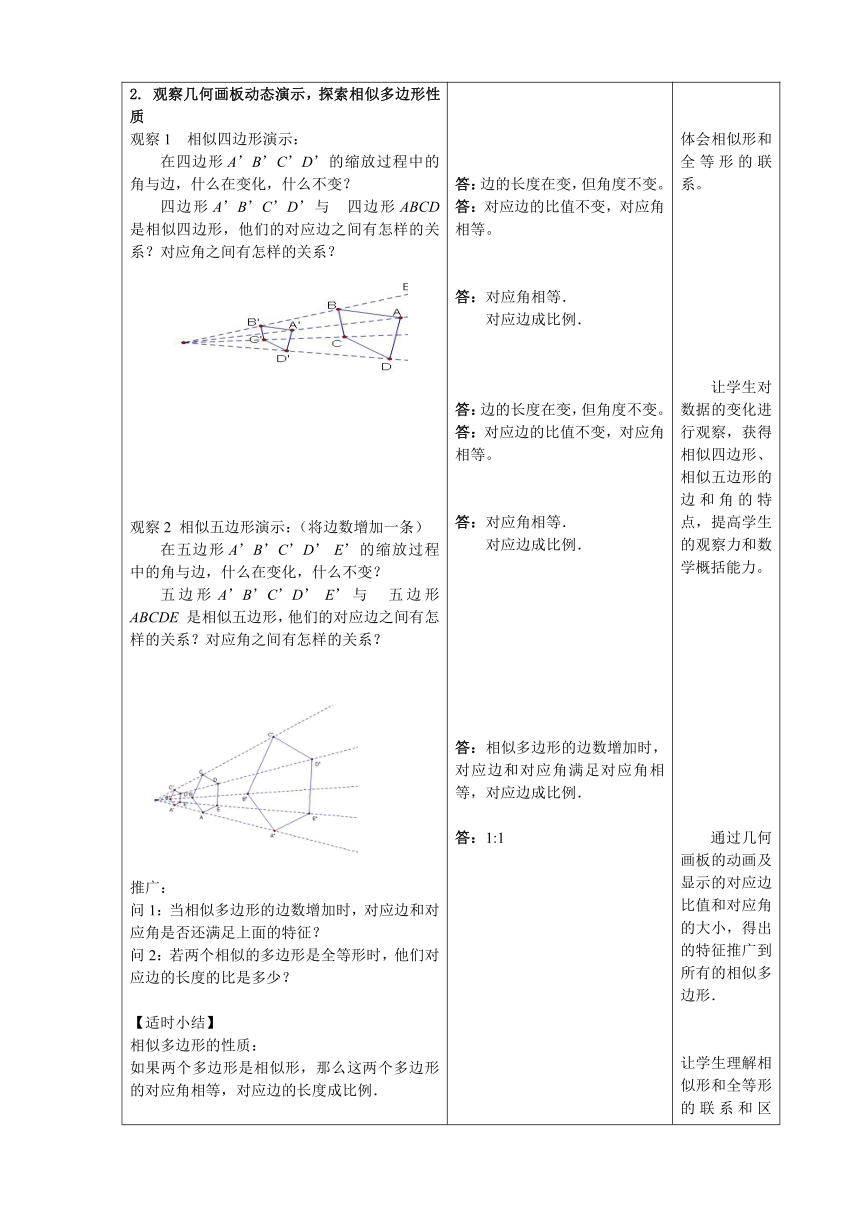
相似四边形演示:
在四边形A’B’C’D’的缩放过程中的角与边,什么在变化,什么不变?
四边形A’B’C’D’与?四边形ABCD
是相似四边形,他们的对应边之间有怎样的关系?对应角之间有怎样的关系?
观察2
相似五边形演示:(将边数增加一条)
在五边形A’B’C’D’
E’的缩放过程中的角与边,什么在变化,什么不变?
五边形A’B’C’D’
E’与?五边形ABCDE
是相似五边形,他们的对应边之间有怎样的关系?对应角之间有怎样的关系?
推广:
问1:当相似多边形的边数增加时,对应边和对应角是否还满足上面的特征?
问2:若两个相似的多边形是全等形时,他们对应边的长度的比是多少?
【适时小结】
相似多边形的性质:
如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例.
4、例题
1)在下列方格图中,分别画出△ABC和四边形ABCD的一个相似图形.
2)判断,并说明理由.
(1)两个直角三角形一定是相似图形.
(2)两个等边三角形一定是相似图形.
(3)有一个角为30°的等腰三角形一定是相似图形.
(4)两个矩形是相似图形.
(5)两个正方形是相似图形.
(6)两个菱形是相似图形.
(7)两个等腰直角三角形是相似图形.
5、例题
如图,四边形ABCD和四边形是相似的图形,点A与点A’、点B与点B’、
点C与点C’、点D与点D’是对应顶点,已知BC=3,CD=2.4,A’B’=2.2,B’C’=2,∠B=70°,∠C=110°,∠D=90°,求边AB、C’D’的长和∠A’的度数.
分析:
读题,并将已知条件标在图上.
解:∵四边形ABCD与四边形A’B’C’D’是相似图形.
∴∠A=∠A’、(两个相似多边形对应角相等、对应边的长度成比例).
由BC=3,CD=2.4,A’B’=2.2,B’C’=2,
得.
解得AB=3.3,C’D’=1.6.
在四边形ABCD中,∠A+∠B+∠C+∠D=360°.
由∠B=70°,∠C=110°,∠D=90°,
得∠A=90°.
于是∠A’=90°.
泰勒斯游学埃及时利用相似三角形测量金字塔高度,泰勒斯是如何“计算”出来的呢?现在你们明白了?
6、课堂练习
已知四边形ABCD与四边形A’B’C’D’是相似的图形,点A与点A’、点B与点B’、
点C与点C’、点D与点D’是对应顶点,其中AB、BC、CD、DA的长分别为12厘米、16厘米、16厘米、20厘米,A’B’的长为9厘米,求B’C’、C’D’、D’A’的长.
一张长方形纸片对折后所得的长方形与原长方形是相似形,则原长方形的长与宽的比是多少?
三、课堂小结
1、本节课你有什么收获?
四、布置作业
练习册:习题24.1
答:边边边、边角边、角边角、角角边.(H.L只用于直角三角形)
答:不能.
答:两个边长不同的等边三角形.
答:它们的形状一样,大小不一样.
答:这些图形形状一样,大小有的一样,有的不一样.
答:相似形(学生说不出,老师引出)
预设生答:
相似形:我们把形状相同的两个图形说成是相似的图形,或者就说是相似形.
如果学生不能表述清楚,教师补充.
是相似形。
答:边的长度在变,但角度不变。
答:对应边的比值不变,对应角相等。
答:对应角相等.
对应边成比例.
答:边的长度在变,但角度不变。
答:对应边的比值不变,对应角相等。
答:对应角相等.
对应边成比例.
答:相似多边形的边数增加时,对应边和对应角满足对应角相等,对应边成比例.
答:1:1
引导学生利用相似多边形的性质,将边长缩小一定的倍数。
答:
(1)×
(2)√
(3)×
(4)×
(5)√
(6)×
(7)√
利用相似图形对应边的长度成比例。
解:
∵四边形ABCD与四边形A’B’C’D’是相似图形.
∴(两个相似多边形对应角相等、对应边的长度成比例).
由AB=12、BC=16、CD=16、DA=20、A’B’=9,
得
解得:B’C’=12厘米
C’D’=12厘米
D’A’=15厘米
请一位学生板演,进行纠错和反馈.
1、相似形的定义:形状相同的两个图形叫做相似的图形,或者相似形.
2、相似形与全等形的关系:
相似形
全等形
一定
3、相似形的性质:
对应角相等,对应边的长度成比例.
以学生熟悉的全等三角形的判定方法和熟悉的等腰直角三角板引入,一方面从全等三角形的判定方法引入,有助于学生建立全等形和相似形的联系,另一方面,让学生通过观察,直观的认识形状相同的图形.
自然引出本节新课内容—相似形
培养学生数学语言的表达和归纳能力.
体会相似形和全等形的联系。
让学生对数据的变化进行观察,获得相似四边形、相似五边形的边和角的特点,提高学生的观察力和数学概括能力。
通过几何画板的动画及显示的对应边比值和对应角的大小,得出的特征推广到所有的相似多边形.
让学生理解相似形和全等形的联系和区别,知道两个多边形全等是两个多边形相似的特殊情况,注意它们之间的联系.
通过开放性的题目,让学生进一步巩固相似多边形的特征.
通过辨析,进一步加深对相似多边形特征的认识.
本题是关于相似多边形的性质及四边形内角和性质运用的几何计算题,帮助学生进一步认识相似多边形的特征和性质.
通过课堂练习,进一步巩固相似多边形性质的应用.
师引导画出图形,建模解决问题。
放缩与相似形
教学目标:
1.能用图形放缩运动的观点认识相似形的意义.
2.知道相似形的概念,理解相似多边形的对应角、对应边的含义.
3.通过对进行放缩运动的图形进行度量分析,认识放缩运动中的不变量,知道相似多边形的特征以及相似形与全等形的关系.
教学重点和难点:
相似形的意义及性质
教学过程:
教师活动
学生活动
教学设计意图
引入
问1.证明三角形全等有哪些方法?
问2.能用角角角证明两个三角形全等吗?如果不能,请举出反例
问3.
这两个等边三角形有什么特点?
问4.
以上四组图形用什么共性?
问5.
我们给具备这种特性的两个图形一个什么名称呢?
学习新知
1、相似形的定义
问6:你能说出相似形的概念吗?
(教师要特别强调形状相同即可,大小可以相同也可以不相同)
问7:
两个全等形是相似形吗?
2.
观察几何画板动态演示,探索相似多边形性质
观察1
相似四边形演示:
在四边形A’B’C’D’的缩放过程中的角与边,什么在变化,什么不变?
四边形A’B’C’D’与?四边形ABCD
是相似四边形,他们的对应边之间有怎样的关系?对应角之间有怎样的关系?
观察2
相似五边形演示:(将边数增加一条)
在五边形A’B’C’D’
E’的缩放过程中的角与边,什么在变化,什么不变?
五边形A’B’C’D’
E’与?五边形ABCDE
是相似五边形,他们的对应边之间有怎样的关系?对应角之间有怎样的关系?
推广:
问1:当相似多边形的边数增加时,对应边和对应角是否还满足上面的特征?
问2:若两个相似的多边形是全等形时,他们对应边的长度的比是多少?
【适时小结】
相似多边形的性质:
如果两个多边形是相似形,那么这两个多边形的对应角相等,对应边的长度成比例.
4、例题
1)在下列方格图中,分别画出△ABC和四边形ABCD的一个相似图形.
2)判断,并说明理由.
(1)两个直角三角形一定是相似图形.
(2)两个等边三角形一定是相似图形.
(3)有一个角为30°的等腰三角形一定是相似图形.
(4)两个矩形是相似图形.
(5)两个正方形是相似图形.
(6)两个菱形是相似图形.
(7)两个等腰直角三角形是相似图形.
5、例题
如图,四边形ABCD和四边形是相似的图形,点A与点A’、点B与点B’、
点C与点C’、点D与点D’是对应顶点,已知BC=3,CD=2.4,A’B’=2.2,B’C’=2,∠B=70°,∠C=110°,∠D=90°,求边AB、C’D’的长和∠A’的度数.
分析:
读题,并将已知条件标在图上.
解:∵四边形ABCD与四边形A’B’C’D’是相似图形.
∴∠A=∠A’、(两个相似多边形对应角相等、对应边的长度成比例).
由BC=3,CD=2.4,A’B’=2.2,B’C’=2,
得.
解得AB=3.3,C’D’=1.6.
在四边形ABCD中,∠A+∠B+∠C+∠D=360°.
由∠B=70°,∠C=110°,∠D=90°,
得∠A=90°.
于是∠A’=90°.
泰勒斯游学埃及时利用相似三角形测量金字塔高度,泰勒斯是如何“计算”出来的呢?现在你们明白了?
6、课堂练习
已知四边形ABCD与四边形A’B’C’D’是相似的图形,点A与点A’、点B与点B’、
点C与点C’、点D与点D’是对应顶点,其中AB、BC、CD、DA的长分别为12厘米、16厘米、16厘米、20厘米,A’B’的长为9厘米,求B’C’、C’D’、D’A’的长.
一张长方形纸片对折后所得的长方形与原长方形是相似形,则原长方形的长与宽的比是多少?
三、课堂小结
1、本节课你有什么收获?
四、布置作业
练习册:习题24.1
答:边边边、边角边、角边角、角角边.(H.L只用于直角三角形)
答:不能.
答:两个边长不同的等边三角形.
答:它们的形状一样,大小不一样.
答:这些图形形状一样,大小有的一样,有的不一样.
答:相似形(学生说不出,老师引出)
预设生答:
相似形:我们把形状相同的两个图形说成是相似的图形,或者就说是相似形.
如果学生不能表述清楚,教师补充.
是相似形。
答:边的长度在变,但角度不变。
答:对应边的比值不变,对应角相等。
答:对应角相等.
对应边成比例.
答:边的长度在变,但角度不变。
答:对应边的比值不变,对应角相等。
答:对应角相等.
对应边成比例.
答:相似多边形的边数增加时,对应边和对应角满足对应角相等,对应边成比例.
答:1:1
引导学生利用相似多边形的性质,将边长缩小一定的倍数。
答:
(1)×
(2)√
(3)×
(4)×
(5)√
(6)×
(7)√
利用相似图形对应边的长度成比例。
解:
∵四边形ABCD与四边形A’B’C’D’是相似图形.
∴(两个相似多边形对应角相等、对应边的长度成比例).
由AB=12、BC=16、CD=16、DA=20、A’B’=9,
得
解得:B’C’=12厘米
C’D’=12厘米
D’A’=15厘米
请一位学生板演,进行纠错和反馈.
1、相似形的定义:形状相同的两个图形叫做相似的图形,或者相似形.
2、相似形与全等形的关系:
相似形
全等形
一定
3、相似形的性质:
对应角相等,对应边的长度成比例.
以学生熟悉的全等三角形的判定方法和熟悉的等腰直角三角板引入,一方面从全等三角形的判定方法引入,有助于学生建立全等形和相似形的联系,另一方面,让学生通过观察,直观的认识形状相同的图形.
自然引出本节新课内容—相似形
培养学生数学语言的表达和归纳能力.
体会相似形和全等形的联系。
让学生对数据的变化进行观察,获得相似四边形、相似五边形的边和角的特点,提高学生的观察力和数学概括能力。
通过几何画板的动画及显示的对应边比值和对应角的大小,得出的特征推广到所有的相似多边形.
让学生理解相似形和全等形的联系和区别,知道两个多边形全等是两个多边形相似的特殊情况,注意它们之间的联系.
通过开放性的题目,让学生进一步巩固相似多边形的特征.
通过辨析,进一步加深对相似多边形特征的认识.
本题是关于相似多边形的性质及四边形内角和性质运用的几何计算题,帮助学生进一步认识相似多边形的特征和性质.
通过课堂练习,进一步巩固相似多边形性质的应用.
师引导画出图形,建模解决问题。
