11.2旋转-沪教版(上海)七年级数学上册课件(共26张ppt)
文档属性
| 名称 | 11.2旋转-沪教版(上海)七年级数学上册课件(共26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:33:59 | ||
图片预览






文档简介
11.2 旋 转
A
B
O
A′
B′
90°
线段AB绕点O,
按照逆时针方向,
转动90度到线段A′B′.
【观察】
A
B
O
△OAB绕点O,
按照逆时针方向,
转动120度到△ O A' B' .
A
B
A '
B'
120°
【观察】
O
A
B
A '
B'
120°
A
O
A′
45°
A
B
O
A′
B′
90°
A
B
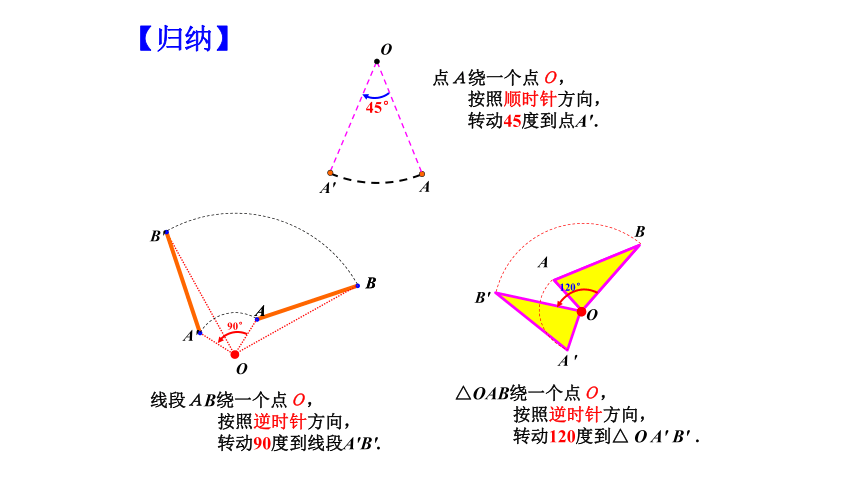
点A绕一个点O,
按照顺时针方向,
转动45度到点A′.
△OAB绕一个点O,
按照逆时针方向,
转动120度到△ O A' B' .
线段AB绕一个点O,
按照逆时针方向,
转动90度到线段A′B′.
【归纳】
这个定点
叫做旋转中心,
旋转角
旋转中心
在平面内,将一个图形上的所有点绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转.
转动的角度
叫做旋转角.
O
A
A1
A
B
C
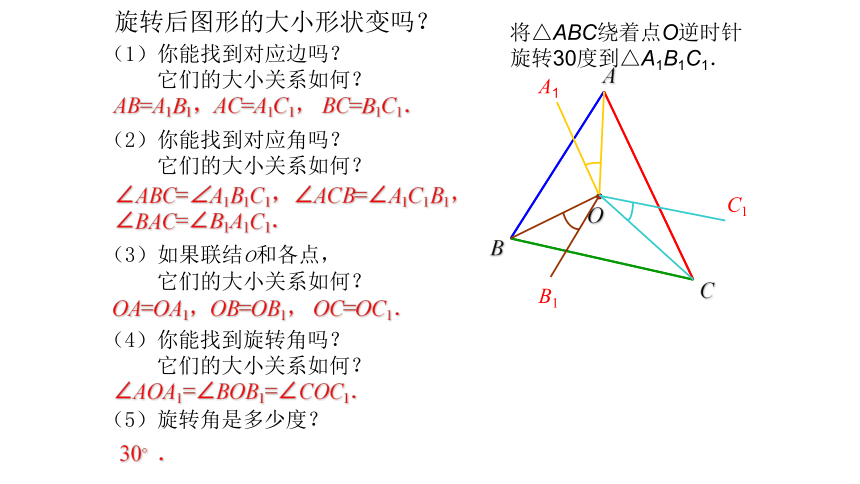
AB=A1B1,AC=A1C1, BC=B1C1.
旋转后图形的大小形状变吗?
A1
O
B1
C1
(1)你能找到对应边吗?
它们的大小关系如何?
(2)你能找到对应角吗?
它们的大小关系如何?
∠ABC=∠A1B1C1,∠ACB=∠A1C1B1,
∠BAC=∠B1A1C1.
(3)如果联结o和各点,
它们的大小关系如何?
将△ABC绕着点O逆时针
旋转30度到△A1B1C1.
OA=OA1,OB=OB1, OC=OC1.
(4)你能找到旋转角吗?
它们的大小关系如何?
∠AOA1=∠BOB1=∠COC1.
(5)旋转角是多少度?
30°.
图形旋转的性质
(1)旋转不改变图形的 和 ;
(2)对应线段 相等;
(3)对应角的 相等;
(4)对应点到旋转中心的 相等;
(5)任意一对对应点与旋转中心的连线所 成的角(旋转角)都 .
大小
度数
形状
长度
距离
相等
A
B
O
A′
B′
旋转中心是___________;
旋转方向是___________;
旋转角是________________.
点O
顺时针
∠AOA′
、∠BOB′
【例1】
如图,△OAB绕点O,旋转到△OA′ B′.
点A的对应点是________,
点B的对应点是________;
OA的对应线段是_______,
AB的对应线段是_______,
OB的对应线段是_______;
∠A的对应角是_______,
∠B的对应角是_______,
∠AOB的对应角是_________.
点A′
点 B′
OA ′
A ′ B ′
OB ′
∠A′
∠B′
∠A′OB′
60°
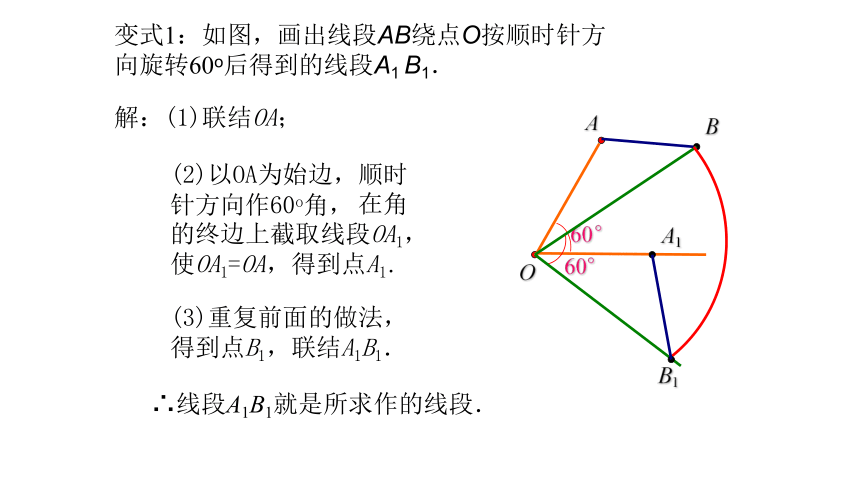
变式1:如图,画出线段AB绕点O按顺时针方向旋转60o后得到的线段A1 B1.
解:(1)联结OA;
O
A
A1
(2)以OA为始边,顺时针方向作60o角,
在角
的终边上截取线段OA1,使OA1=OA,得到点A1.
∴线段A1B1就是所求作的线段.
B
(3)重复前面的做法,得到点B1,联结A1B1.
60°
B1
60°
变式2:如图,画出△ABC绕点O按顺时针方向旋转60o后得到的△A1 B1C1.
解:(1)联结OA;
O
A
A1
(2)以OA为始边,顺时针方向作60o角,
在角
的终边上截取线段OA1,使OA1=OA,得到点A1.
∴△A1B1C1就是所求作的三角形.
B
(3)重复前面的做法,得到点B1.
60°
B1
(4)重复前面的做法,得到点C1,顺次联结A1B1C1.
C
C1
如果是画出四边形ABCD绕点O按顺时针方向旋转60o后的图形,怎么画?
C′
A′
B′
O
B
A
C
旋转前后图形的形状、大小______.
量一量:
OA与O A′,
OB与O B′,
OC与O C′的长度.
对应点到旋转中心的距离_______.
量一量:
∠AO A′、
∠BO B′、
∠CO C′的度数.
每组对应点与旋转中心的连线所夹的旋转角,它们的大小_______.
对应线段的长度、对应角的大小_______.
图形的位置发生了______.
D
D′
旋转的性质:
不变
相等
变化
相等
相等
如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF.
M′
M
F
E
B
C
D
(2)旋转角是________度.
(1)旋转中心是点_______.
(3)连结EF,△AEF是_____________三角形.
(4)点M是AD的中点,经上述旋转后,
②点M在旋转时经过的路线是怎样的图形?
③线段AM所扫过的平面部分是怎样的图形?
①点M转到什么位置?
A
90
等腰直角
AB的中点
圆弧
扇形
【练习】
A
如图,已知点A和点O,请画出点A绕点O按顺时针旋转90°后的图形.
A
O
【例2】
【变式】
如图,画按顺时针旋转90°后的图形.出三角形ABC绕点O
O
B
A
C
【练习】
如图,内圆的面积为5平方厘米,外圆的面积为65平方厘米,你能求出阴影部分的面积和吗?
45°
例题:在图中,画出三角形ABC绕点O按逆时针方向旋转45o后的图形.
解:(1)联结OA、OB、OC ;
O
A
A1
(2)以OA为始边,逆时针方向作45o角,
在角
的终边上截取线段OA1,使OA1=OA,得到点A1 ;
∴△A1B1C1就是所求作的三角形.
B
(3)重复前面的做法,得到点B1 、 C1 ;
B1
C
C1
(4)顺次联结点A1 、 B1 、 C1 ;
如果三角形ABC绕点O旋转360o后会怎样?
问题 如图,将一张正方形纸片平放在纸上,沿四边画出它的初始位置和正方形的两条对角线,在对角线的公共点上用大头针钉住.旋转正方形,最少旋转几度可以使它与初始位置的正方形重合?
每转多少度会重复上述现象?
A ′
B ′
C ′
D ′
A
B
C
D
O
正方形最少旋转_____,能与初始图形重合.
旋转前后图形的形状、大小_____.
【思维拓展】
90°
不变
每转90°会重复上述现象.
B
B
问题 如图,在两张透明的纸上用圆规画出两个大小相同的圆A、圆B,然后把一张纸盖在另一张上,使两个圆重合,任意选一点F,用一根大头针钉在点F上,旋转其中一个圆B,直到圆B第一次完全盖住圆A,这时圆B旋转了多少度?
一个图形绕任意一点 ,都能与初始图形_____.
A
旋转前后图形的形状、大小______.
F
【思维拓展】
旋转360°
重合
不变
1、相同:
B
A
C
O
2、不同:
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或逆时针
转动一定的角度
平移和旋转的异同:
都是一种运动;运动前后 不改变图形的形状和大小
获取新知
三角形绕点旋转加平移
例题讲解
随堂演练
【归纳总结】旋转性质的“两应用”
(1)应用一:判断线段或角是否相等.
①根据旋转角相等,对应点与旋转中心的连线相等可得角或线段相等;
②根据旋转后的图形与原来图形的形状、大小都相同可得图形的对应线段、对应角相等.
(2)应用二:计算图形的面积、线段的长度或角的大小.
随堂演练
获取新知
作旋转变换后的图形:
(1)先确定图形的关键点和(定点)旋转中心
(2)分别连接关键点和定点
(3)利用旋转性质作出关键点的对应点(根据旋转方向和旋转角度作出)
(3)按照原图形中的连接方法顺次连接各对应点,要注意旋转中心,旋转方向和旋转角
随堂演练
A
B'
OB'
A'B'
∠A'
∠B'
O
60
随堂演练
垂直
40
4.钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心.
(2)经过20分,分针旋转了多少度?
解析:(1)它的旋转中心是钟表的轴心.
(2)分针匀速旋转一周需要60分,因此旋转20分,分针旋转的角度为 .
自主小结
旋转的概念 :
旋转的性质 :
在平面内,将一个图形上的所有点绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转.这个定点叫做旋转中心,转动的角度叫做旋转角.
(1)旋转不改变图形的大小和形状;
(2)对应线段长度相等;
(3)对应角的度数相等;
(4)对应点到旋转中心的距离相等 ;
(5)任意一对对应点与旋转中心的连线所成的角(旋转角)都相等.
A
B
O
A′
B′
90°
线段AB绕点O,
按照逆时针方向,
转动90度到线段A′B′.
【观察】
A
B
O
△OAB绕点O,
按照逆时针方向,
转动120度到△ O A' B' .
A
B
A '
B'
120°
【观察】
O
A
B
A '
B'
120°
A
O
A′
45°
A
B
O
A′
B′
90°
A
B
点A绕一个点O,
按照顺时针方向,
转动45度到点A′.
△OAB绕一个点O,
按照逆时针方向,
转动120度到△ O A' B' .
线段AB绕一个点O,
按照逆时针方向,
转动90度到线段A′B′.
【归纳】
这个定点
叫做旋转中心,
旋转角
旋转中心
在平面内,将一个图形上的所有点绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转.
转动的角度
叫做旋转角.
O
A
A1
A
B
C
AB=A1B1,AC=A1C1, BC=B1C1.
旋转后图形的大小形状变吗?
A1
O
B1
C1
(1)你能找到对应边吗?
它们的大小关系如何?
(2)你能找到对应角吗?
它们的大小关系如何?
∠ABC=∠A1B1C1,∠ACB=∠A1C1B1,
∠BAC=∠B1A1C1.
(3)如果联结o和各点,
它们的大小关系如何?
将△ABC绕着点O逆时针
旋转30度到△A1B1C1.
OA=OA1,OB=OB1, OC=OC1.
(4)你能找到旋转角吗?
它们的大小关系如何?
∠AOA1=∠BOB1=∠COC1.
(5)旋转角是多少度?
30°.
图形旋转的性质
(1)旋转不改变图形的 和 ;
(2)对应线段 相等;
(3)对应角的 相等;
(4)对应点到旋转中心的 相等;
(5)任意一对对应点与旋转中心的连线所 成的角(旋转角)都 .
大小
度数
形状
长度
距离
相等
A
B
O
A′
B′
旋转中心是___________;
旋转方向是___________;
旋转角是________________.
点O
顺时针
∠AOA′
、∠BOB′
【例1】
如图,△OAB绕点O,旋转到△OA′ B′.
点A的对应点是________,
点B的对应点是________;
OA的对应线段是_______,
AB的对应线段是_______,
OB的对应线段是_______;
∠A的对应角是_______,
∠B的对应角是_______,
∠AOB的对应角是_________.
点A′
点 B′
OA ′
A ′ B ′
OB ′
∠A′
∠B′
∠A′OB′
60°
变式1:如图,画出线段AB绕点O按顺时针方向旋转60o后得到的线段A1 B1.
解:(1)联结OA;
O
A
A1
(2)以OA为始边,顺时针方向作60o角,
在角
的终边上截取线段OA1,使OA1=OA,得到点A1.
∴线段A1B1就是所求作的线段.
B
(3)重复前面的做法,得到点B1,联结A1B1.
60°
B1
60°
变式2:如图,画出△ABC绕点O按顺时针方向旋转60o后得到的△A1 B1C1.
解:(1)联结OA;
O
A
A1
(2)以OA为始边,顺时针方向作60o角,
在角
的终边上截取线段OA1,使OA1=OA,得到点A1.
∴△A1B1C1就是所求作的三角形.
B
(3)重复前面的做法,得到点B1.
60°
B1
(4)重复前面的做法,得到点C1,顺次联结A1B1C1.
C
C1
如果是画出四边形ABCD绕点O按顺时针方向旋转60o后的图形,怎么画?
C′
A′
B′
O
B
A
C
旋转前后图形的形状、大小______.
量一量:
OA与O A′,
OB与O B′,
OC与O C′的长度.
对应点到旋转中心的距离_______.
量一量:
∠AO A′、
∠BO B′、
∠CO C′的度数.
每组对应点与旋转中心的连线所夹的旋转角,它们的大小_______.
对应线段的长度、对应角的大小_______.
图形的位置发生了______.
D
D′
旋转的性质:
不变
相等
变化
相等
相等
如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF.
M′
M
F
E
B
C
D
(2)旋转角是________度.
(1)旋转中心是点_______.
(3)连结EF,△AEF是_____________三角形.
(4)点M是AD的中点,经上述旋转后,
②点M在旋转时经过的路线是怎样的图形?
③线段AM所扫过的平面部分是怎样的图形?
①点M转到什么位置?
A
90
等腰直角
AB的中点
圆弧
扇形
【练习】
A
如图,已知点A和点O,请画出点A绕点O按顺时针旋转90°后的图形.
A
O
【例2】
【变式】
如图,画按顺时针旋转90°后的图形.出三角形ABC绕点O
O
B
A
C
【练习】
如图,内圆的面积为5平方厘米,外圆的面积为65平方厘米,你能求出阴影部分的面积和吗?
45°
例题:在图中,画出三角形ABC绕点O按逆时针方向旋转45o后的图形.
解:(1)联结OA、OB、OC ;
O
A
A1
(2)以OA为始边,逆时针方向作45o角,
在角
的终边上截取线段OA1,使OA1=OA,得到点A1 ;
∴△A1B1C1就是所求作的三角形.
B
(3)重复前面的做法,得到点B1 、 C1 ;
B1
C
C1
(4)顺次联结点A1 、 B1 、 C1 ;
如果三角形ABC绕点O旋转360o后会怎样?
问题 如图,将一张正方形纸片平放在纸上,沿四边画出它的初始位置和正方形的两条对角线,在对角线的公共点上用大头针钉住.旋转正方形,最少旋转几度可以使它与初始位置的正方形重合?
每转多少度会重复上述现象?
A ′
B ′
C ′
D ′
A
B
C
D
O
正方形最少旋转_____,能与初始图形重合.
旋转前后图形的形状、大小_____.
【思维拓展】
90°
不变
每转90°会重复上述现象.
B
B
问题 如图,在两张透明的纸上用圆规画出两个大小相同的圆A、圆B,然后把一张纸盖在另一张上,使两个圆重合,任意选一点F,用一根大头针钉在点F上,旋转其中一个圆B,直到圆B第一次完全盖住圆A,这时圆B旋转了多少度?
一个图形绕任意一点 ,都能与初始图形_____.
A
旋转前后图形的形状、大小______.
F
【思维拓展】
旋转360°
重合
不变
1、相同:
B
A
C
O
2、不同:
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或逆时针
转动一定的角度
平移和旋转的异同:
都是一种运动;运动前后 不改变图形的形状和大小
获取新知
三角形绕点旋转加平移
例题讲解
随堂演练
【归纳总结】旋转性质的“两应用”
(1)应用一:判断线段或角是否相等.
①根据旋转角相等,对应点与旋转中心的连线相等可得角或线段相等;
②根据旋转后的图形与原来图形的形状、大小都相同可得图形的对应线段、对应角相等.
(2)应用二:计算图形的面积、线段的长度或角的大小.
随堂演练
获取新知
作旋转变换后的图形:
(1)先确定图形的关键点和(定点)旋转中心
(2)分别连接关键点和定点
(3)利用旋转性质作出关键点的对应点(根据旋转方向和旋转角度作出)
(3)按照原图形中的连接方法顺次连接各对应点,要注意旋转中心,旋转方向和旋转角
随堂演练
A
B'
OB'
A'B'
∠A'
∠B'
O
60
随堂演练
垂直
40
4.钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心.
(2)经过20分,分针旋转了多少度?
解析:(1)它的旋转中心是钟表的轴心.
(2)分针匀速旋转一周需要60分,因此旋转20分,分针旋转的角度为 .
自主小结
旋转的概念 :
旋转的性质 :
在平面内,将一个图形上的所有点绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转.这个定点叫做旋转中心,转动的角度叫做旋转角.
(1)旋转不改变图形的大小和形状;
(2)对应线段长度相等;
(3)对应角的度数相等;
(4)对应点到旋转中心的距离相等 ;
(5)任意一对对应点与旋转中心的连线所成的角(旋转角)都相等.
