北师大版八年级数学上册第六章数据的分析复习课课件(共22张ppt)
文档属性
| 名称 | 北师大版八年级数学上册第六章数据的分析复习课课件(共22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:32:18 | ||
图片预览






文档简介
北师大版八年级数学上册
第六章数据的分析复习课
1.能说出并掌握算术平均数、加权平均数的概念,会求一组数据的算术平均数和加权平均数。
2.能说出中位数、众数的定义,会求一组数据的中位数、众数;体会平均数、中位数、众数三者的差别;
3.了解刻画数据离散程度的三个量度—极差、方差、标准差;能借助计算器求出相应的数值,并在具体问题情境中加以应用。
4. 能从各类统计图中获取数据,初步选取恰当的数据代表作为自己的判断,通过实例体会用样本估计总体的思想。
4、通过复习提高归纳整理的能力
学习目标
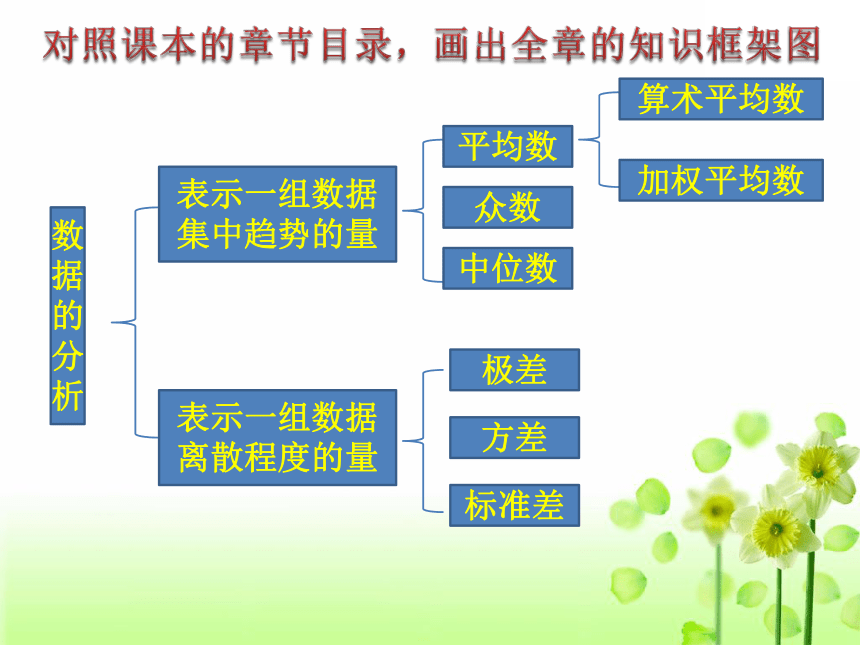
对照课本的章节目录,画出全章的知识框架图
数据的分析
表示一组数据集中趋势的量
表示一组数据离散程度的量
平均数
众数
中位数
算术平均数
加权平均数
极差
方差
标准差
1、数学期末总评成绩由作业分数,课堂参与分数,期考分数三部分组成,并按3:3:4的比例确定。已知小明的作业90分,课堂参与85分,期考80分,则他的总评成绩为______。
练习
84.5
=84.5
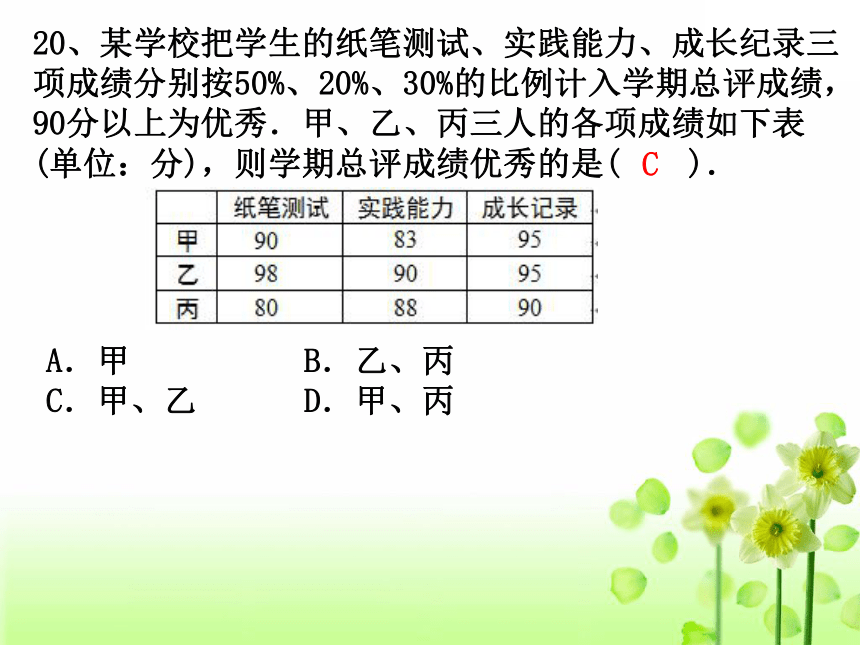
20、某学校把学生的纸笔测试、实践能力、成长纪录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),则学期总评成绩优秀的是( ).
A.甲 B.乙、丙 C.甲、乙 D.甲、丙
C
2.一组数据为:3,5,7,8,8,则这组数据的中位数
是 ,众数是 。
7
8
2
3、已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是 。
中位数:(1)从小到大排序;
(2)共有5个(奇数)个数据,取最中间的一个数据。
众数:出现次数最多的数
(1)求平均数 (1+3+5+x+2)÷5=3
解得x=4
(2)求方差:
每人销售量(单位:件)
600
500
400
350
300
200
人数(单位:人)
1
4
4
6
7
3
4、一组数据5,-2,3,x,3,-2,若每个数据都是这组数据的众数,则这组数据的平均数是 。
5、某公司销售部有营销人员25人,销售部为了制定某种商品的销售定额,统计了这25人某月的销售量如下表:
公司营销人员该月销售量的中位数是( )。
A.400件 B.350件 C.300件 D.360件
1.4
B
6、一个样本的方差是
那么这个样本的平均数为 ,共有 个数据。
7、关于一组数据的平均数、中位数、众数,下列说法中正确的是( )
A.平均数一定是这组数中的某个数
B. 中位数一定是这组数中的某个数
C.众数一定是这组数中的某个数
D.以上说法都不对
5
6
C
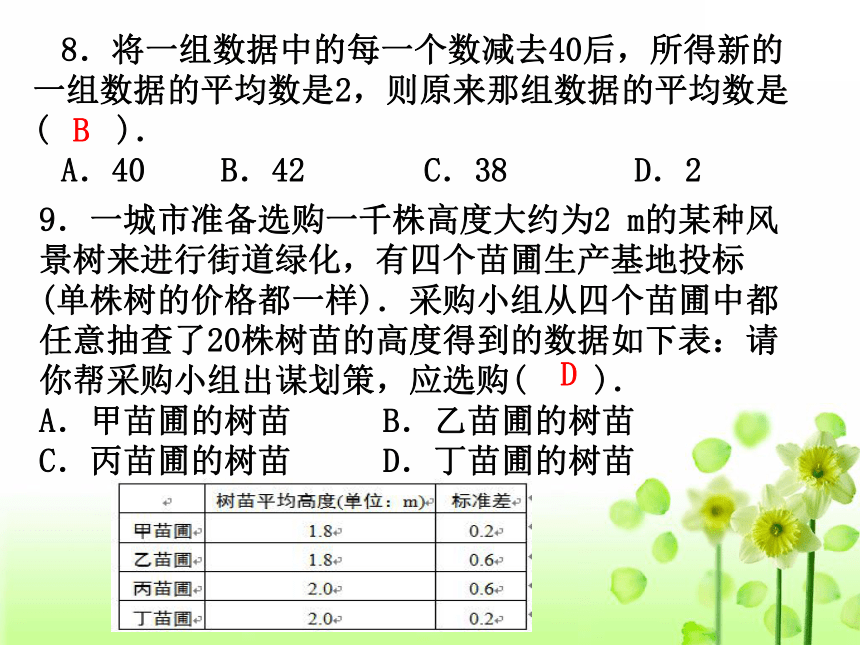
8.将一组数据中的每一个数减去40后,所得新的一组数据的平均数是2,则原来那组数据的平均数是( ).
A.40 B.42 C.38 D.2
9.一城市准备选购一千株高度大约为2 m的某种风景树来进行街道绿化,有四个苗圃生产基地投标(单株树的价格都一样).采购小组从四个苗圃中都任意抽查了20株树苗的高度得到的数据如下表:请你帮采购小组出谋划策,应选购( ).
A.甲苗圃的树苗 B.乙苗圃的树苗
C.丙苗圃的树苗 D.丁苗圃的树苗
B
D
10.一鞋店试销一种新款女鞋,试销期间卖出情况如下表:
对于这个鞋店的经理来说最关心哪种型号的鞋畅销,则下列统计量对鞋店经理来说最有意义的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
B
11.衡量样本和总体的波动大小的特征数是( ).
A.平均数 B.方差 C.众数 D.中位数
12.一个射手连续射靶22次,其中3次射中10环,7次射中9环,9次射中8环,3次射中7环.则该射手射中环数的中位数和众数分别为( ).
A.8环,9环 B.8环, 8环
C.8.5环, 8环 D.8.5环, 9环
B
B
13、某校五个绿化小组一天植树的棵数如下:10,10,12,x, 8.已知这组数据的众数与平均数相等,那么这组数据的中位数是( )
A. 8 B. 9 C. 10 D. 12
C
众数为10,则(10+10+12+x+8)÷5=10
解得x=10
14.下列说法错误的是( ).
A.一组数据的平均数、众数,中位数可能是同一个数
B.一组数据中中位数可能不唯一确定
C.一组数据中平均数、众数、中位数是从不同角度描述了一组数据的集中趋势
D.一组数据中众数可能有多个
B
15.已知x1,x2,x3的平均数=10,方差s2=3,
则(1)2x1,2x2,2x3的平均数为 ,方差为 ;
(2) x1+2,x2+2,x3+2的平均数为 ,方差为 ;
20
12
12
3
16、某同学进行社会调查,随机抽查某地区20个家庭的收入情况,并绘制了统计图请根据统计图给出的信息回答:
(1)填写下表
(2)这20个家庭的年平均收入为 万元。数据中的中位数是 万元,众数是 万元。
1 1 2 3 4 5 3 1
1.6
1.2
1.3
19.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分输入汉字的个数经统计计算后结果如下表:
某同学根据上表分析得出如下结论:
(1)甲、乙两班学生成绩的平均水平相同;
(2)乙班优秀的人数多于甲班优秀的人数;(每分输入汉字≥150个为优秀)
(3)甲班成绩的波动情况比乙班成绩的波动小.
上述结论中正确的是( ).
A.(1)(2)(3) B.(1)(2)
C.(1)(3) D.(2)(3)
B
21.人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下: = =80,
=240, =180,则成绩较为稳定的班级是( ).
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
22.某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整.
(3)在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
(1)该班共有多少名学生?其中穿175型校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整.
解:(1)该班共有学生15÷30%=50名,
其中穿175型校服的学生20%×50=10名
(2)如图:
50-(3+15+15+10+5)=2
(3)2÷50×360=14.4°
(3)在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
答:185型校服所对应的扇形圆心角14.4°
(4)众数是165型和170型,中位数是170型
23、当今,青少年视力水平下降已引起了社会的关注,为了了解某校3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的直方图(长方形的高表示该组人数)如下:解答下列问题:
(1)本次抽样调查共抽测了 名学生?
(2)参加抽测学生的视力的众数在 范围内?
(3)若视力为4.9, 5.0, 5.1及以上为正常,试估计该校学生视力正常的人数约为多少?
(4)求参加抽测学生的平均视力(只列式)
(3)(20+10)÷150×3000=600
(4)(30×4.1+50×4.4+40×4.7+20×5.0+10×5.3)÷150
150
答:该校学生视力正常的人数约为600人
24、国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少?”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h;B组:0.5h≤t<1h;C组:1h≤t<1.5h;
D组:t≥1.5h
请根据上述信息解答下列问题:
(1)C组的人数是______;
(2)本次调查数据的中位数落在______组内;众数落在______组内;
(3)若该辖区约有24000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
300-20-100-60=120
120
C
C
(3)(120+60)÷300×24000
=14400
答:达国家规定体育活动时间的人约有14400人
第六章数据的分析复习课
1.能说出并掌握算术平均数、加权平均数的概念,会求一组数据的算术平均数和加权平均数。
2.能说出中位数、众数的定义,会求一组数据的中位数、众数;体会平均数、中位数、众数三者的差别;
3.了解刻画数据离散程度的三个量度—极差、方差、标准差;能借助计算器求出相应的数值,并在具体问题情境中加以应用。
4. 能从各类统计图中获取数据,初步选取恰当的数据代表作为自己的判断,通过实例体会用样本估计总体的思想。
4、通过复习提高归纳整理的能力
学习目标
对照课本的章节目录,画出全章的知识框架图
数据的分析
表示一组数据集中趋势的量
表示一组数据离散程度的量
平均数
众数
中位数
算术平均数
加权平均数
极差
方差
标准差
1、数学期末总评成绩由作业分数,课堂参与分数,期考分数三部分组成,并按3:3:4的比例确定。已知小明的作业90分,课堂参与85分,期考80分,则他的总评成绩为______。
练习
84.5
=84.5
20、某学校把学生的纸笔测试、实践能力、成长纪录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),则学期总评成绩优秀的是( ).
A.甲 B.乙、丙 C.甲、乙 D.甲、丙
C
2.一组数据为:3,5,7,8,8,则这组数据的中位数
是 ,众数是 。
7
8
2
3、已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是 。
中位数:(1)从小到大排序;
(2)共有5个(奇数)个数据,取最中间的一个数据。
众数:出现次数最多的数
(1)求平均数 (1+3+5+x+2)÷5=3
解得x=4
(2)求方差:
每人销售量(单位:件)
600
500
400
350
300
200
人数(单位:人)
1
4
4
6
7
3
4、一组数据5,-2,3,x,3,-2,若每个数据都是这组数据的众数,则这组数据的平均数是 。
5、某公司销售部有营销人员25人,销售部为了制定某种商品的销售定额,统计了这25人某月的销售量如下表:
公司营销人员该月销售量的中位数是( )。
A.400件 B.350件 C.300件 D.360件
1.4
B
6、一个样本的方差是
那么这个样本的平均数为 ,共有 个数据。
7、关于一组数据的平均数、中位数、众数,下列说法中正确的是( )
A.平均数一定是这组数中的某个数
B. 中位数一定是这组数中的某个数
C.众数一定是这组数中的某个数
D.以上说法都不对
5
6
C
8.将一组数据中的每一个数减去40后,所得新的一组数据的平均数是2,则原来那组数据的平均数是( ).
A.40 B.42 C.38 D.2
9.一城市准备选购一千株高度大约为2 m的某种风景树来进行街道绿化,有四个苗圃生产基地投标(单株树的价格都一样).采购小组从四个苗圃中都任意抽查了20株树苗的高度得到的数据如下表:请你帮采购小组出谋划策,应选购( ).
A.甲苗圃的树苗 B.乙苗圃的树苗
C.丙苗圃的树苗 D.丁苗圃的树苗
B
D
10.一鞋店试销一种新款女鞋,试销期间卖出情况如下表:
对于这个鞋店的经理来说最关心哪种型号的鞋畅销,则下列统计量对鞋店经理来说最有意义的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
B
11.衡量样本和总体的波动大小的特征数是( ).
A.平均数 B.方差 C.众数 D.中位数
12.一个射手连续射靶22次,其中3次射中10环,7次射中9环,9次射中8环,3次射中7环.则该射手射中环数的中位数和众数分别为( ).
A.8环,9环 B.8环, 8环
C.8.5环, 8环 D.8.5环, 9环
B
B
13、某校五个绿化小组一天植树的棵数如下:10,10,12,x, 8.已知这组数据的众数与平均数相等,那么这组数据的中位数是( )
A. 8 B. 9 C. 10 D. 12
C
众数为10,则(10+10+12+x+8)÷5=10
解得x=10
14.下列说法错误的是( ).
A.一组数据的平均数、众数,中位数可能是同一个数
B.一组数据中中位数可能不唯一确定
C.一组数据中平均数、众数、中位数是从不同角度描述了一组数据的集中趋势
D.一组数据中众数可能有多个
B
15.已知x1,x2,x3的平均数=10,方差s2=3,
则(1)2x1,2x2,2x3的平均数为 ,方差为 ;
(2) x1+2,x2+2,x3+2的平均数为 ,方差为 ;
20
12
12
3
16、某同学进行社会调查,随机抽查某地区20个家庭的收入情况,并绘制了统计图请根据统计图给出的信息回答:
(1)填写下表
(2)这20个家庭的年平均收入为 万元。数据中的中位数是 万元,众数是 万元。
1 1 2 3 4 5 3 1
1.6
1.2
1.3
19.甲、乙两班举行电脑汉字输入速度比赛,参赛学生每分输入汉字的个数经统计计算后结果如下表:
某同学根据上表分析得出如下结论:
(1)甲、乙两班学生成绩的平均水平相同;
(2)乙班优秀的人数多于甲班优秀的人数;(每分输入汉字≥150个为优秀)
(3)甲班成绩的波动情况比乙班成绩的波动小.
上述结论中正确的是( ).
A.(1)(2)(3) B.(1)(2)
C.(1)(3) D.(2)(3)
B
21.人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下: = =80,
=240, =180,则成绩较为稳定的班级是( ).
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
22.某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整.
(3)在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
(1)该班共有多少名学生?其中穿175型校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整.
解:(1)该班共有学生15÷30%=50名,
其中穿175型校服的学生20%×50=10名
(2)如图:
50-(3+15+15+10+5)=2
(3)2÷50×360=14.4°
(3)在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
答:185型校服所对应的扇形圆心角14.4°
(4)众数是165型和170型,中位数是170型
23、当今,青少年视力水平下降已引起了社会的关注,为了了解某校3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的直方图(长方形的高表示该组人数)如下:解答下列问题:
(1)本次抽样调查共抽测了 名学生?
(2)参加抽测学生的视力的众数在 范围内?
(3)若视力为4.9, 5.0, 5.1及以上为正常,试估计该校学生视力正常的人数约为多少?
(4)求参加抽测学生的平均视力(只列式)
(3)(20+10)÷150×3000=600
(4)(30×4.1+50×4.4+40×4.7+20×5.0+10×5.3)÷150
150
答:该校学生视力正常的人数约为600人
24、国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少?”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
A组:t<0.5h;B组:0.5h≤t<1h;C组:1h≤t<1.5h;
D组:t≥1.5h
请根据上述信息解答下列问题:
(1)C组的人数是______;
(2)本次调查数据的中位数落在______组内;众数落在______组内;
(3)若该辖区约有24000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
300-20-100-60=120
120
C
C
(3)(120+60)÷300×24000
=14400
答:达国家规定体育活动时间的人约有14400人
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
