初中数学青岛版(2012)八年级上册第二章轴对称复习课件 (1)(共47张ppt)
文档属性
| 名称 | 初中数学青岛版(2012)八年级上册第二章轴对称复习课件 (1)(共47张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 00:00:00 | ||
图片预览








文档简介
《图形的轴对称》的复习
复习方法
1.对整章的学习内容做一回顾,系统地把握全章的知识要点和基本技能。
2.通过例题和练习,能较好地运用本章知识和技能解决有关问题。
重点、难点
判断图形是否是轴对称图形,线段的垂直平分线、角平分线的性质、等腰三角形的性质和判定及其应用是学习重点,而灵活运用上述性质解决问题、轴对称图案的设计是学习难点。
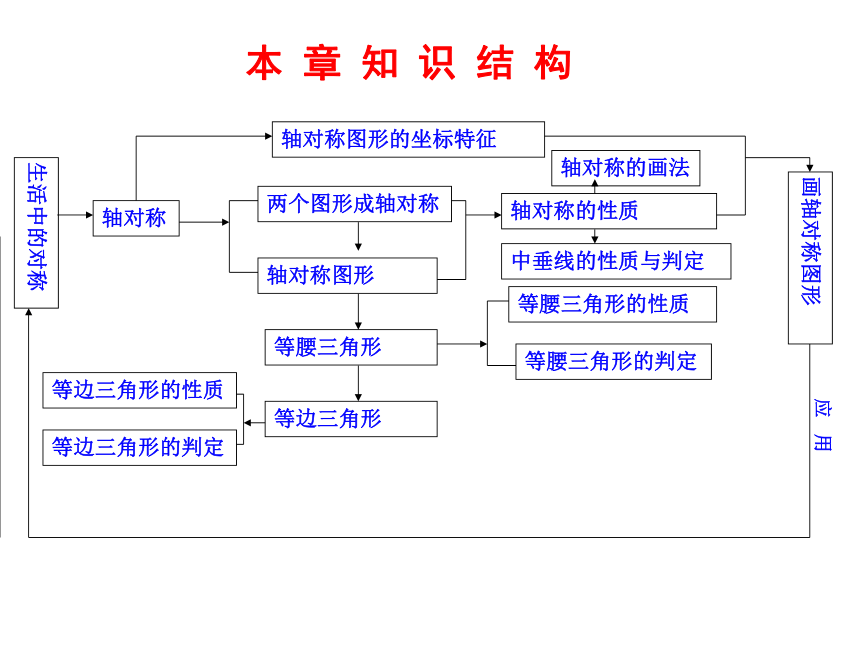
本 章 知 识 结 构
生活中的对称
轴对称
轴对称图形的坐标特征
等边三角形的性质
等边三角形的判定
两个图形成轴对称
轴对称图形
等腰三角形的性质
等腰三角形的判定
等腰三角形
等边三角形
轴对称的性质
中垂线的性质与判定
画轴对称图形
应 用
轴对称的画法
一、知识要点回顾
记牢,别忘了哟!
1.一个图形沿某条直线对折,对折的两部分能 , 那么就称这样的图形为轴对称图形。 2.把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成 。 3.轴对称图形(或关于某条直线对称的两个图形)沿对称轴对折后的两部分是完全重合的,它的 相等, 相等.对称点的连线被对称轴 。4. 并且 一条线段的直线称为这条线段的垂直平分线。线段的垂直平分线上的点到这条线段两个端点的 。
5.角平分线上的点到角两边的距离 。
完全重合
轴对称
对应线段
对应角
垂直平分
垂直
平分
距离相等
相等
6.等腰三角形底边的中线、高线、顶角的平分线 ,等腰三角形的 相等(等边对等角),等边三角形的三个角都等于 °
7.如果一个三角形有两个角相等,那么这两个角所对的边 (等角对等边);有两个角是60°的三角形是 三角形,有一个角是 °的等腰三角形是等边三角形。
互相重合
两个底角
60
也相等
60
等边
记牢,别忘了哟!
轴对称专题
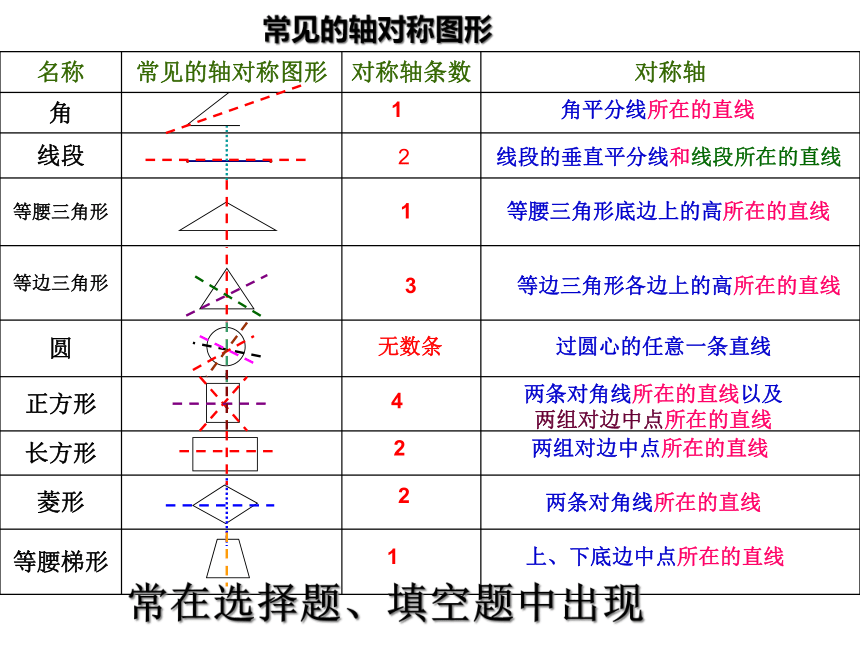
常见的轴对称图形
名称
常见的轴对称图形
对称轴条数
对称轴
角
线段
等腰三角形
等边三角形
圆
正方形
长方形
菱形
等腰梯形
角平分线所在的直线
2
线段的垂直平分线和线段所在的直线
1
等腰三角形底边上的高所在的直线
3
等边三角形各边上的高所在的直线
无数条
过圆心的任意一条直线
4
两条对角线所在的直线以及两组对边中点所在的直线
2
两组对边中点所在的直线
2
两条对角线所在的直线
1
上、下底边中点所在的直线
1
常在选择题、填空题中出现
二、例题精选
例1.下列图案是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
B
举一反三:1、在下列图形中,是轴对称图形的是( )
A、锐角三角形 B、曲线 C、线段 D、直角三角形
2、等腰三角形的对称轴有( )A、一条 B、二条
C、三条 D、一条或三条
3、下列图形中不是轴对称图形的是( )
A、有两个角相等的三角形 B、有一角为45°的直角三角形?
C、有两个角分别为50°与80°的三角形
D、有两个角分别为55°与65°的三角形
C
D
D
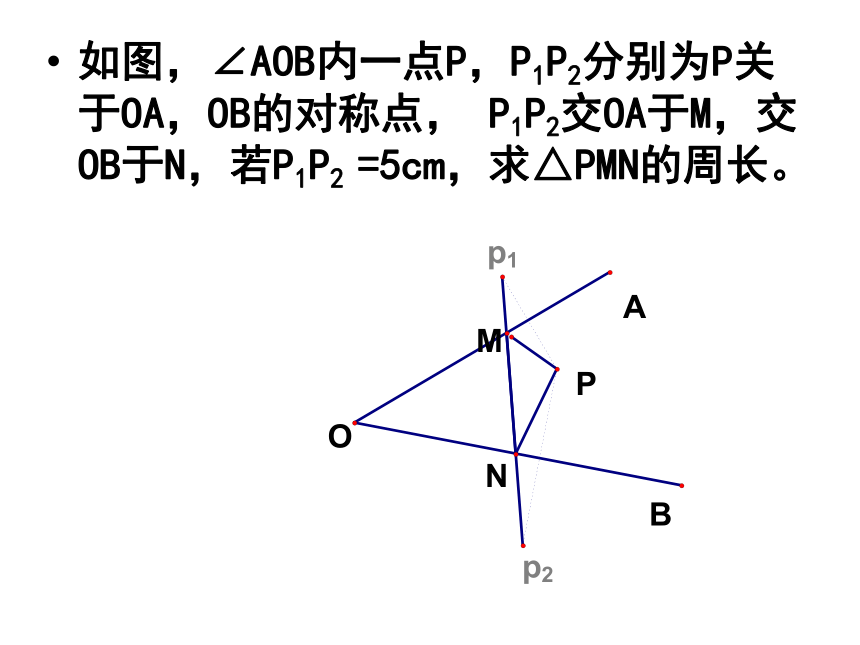
如图,∠AOB内一点P,P1P2分别为P关于OA,OB的对称点, P1P2交OA于M,交OB于N,若P1P2 =5cm,求△PMN的周长。
用坐标表示轴对称小结:
在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(x, - y)
(- x, y)
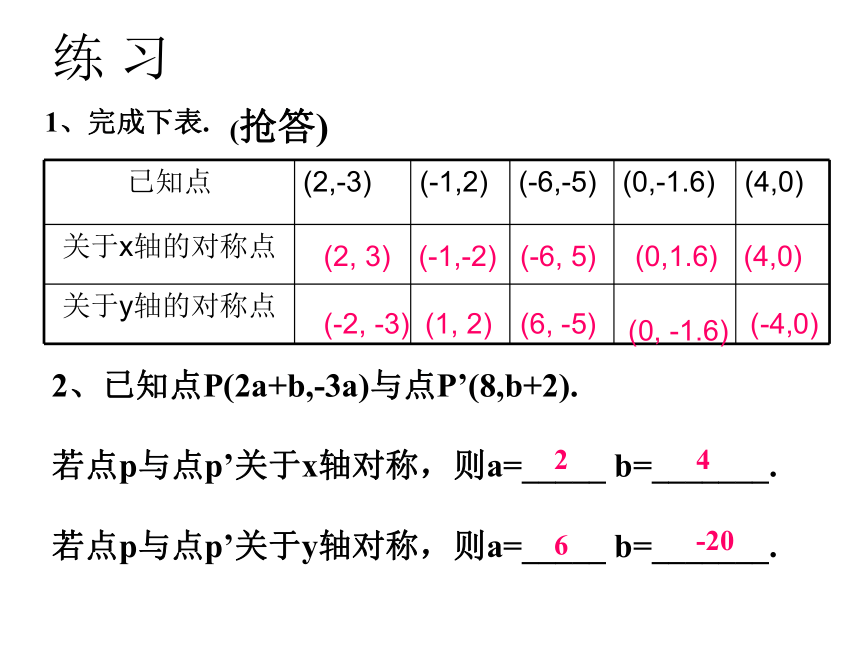
1、完成下表.
已知点
(2,-3)
(-1,2)
(-6,-5)
(0,-1.6)
(4,0)
关于x轴的对称点
关于y轴的对称点
(-2, -3)
(2, 3)
(-1,-2)
(1, 2)
(6, -5)
(-6, 5)
(0, -1.6)
(0,1.6)
(-4,0)
(4,0)
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
练 习
2
4
6
-20
(抢答)
垂直平分线和角平分线专题
基础闯关
1、如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.
E
D
A
B
C
7
60
2、如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____.
A
B
E
D
C
(1)
4
6
基础闯关
3、已知如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长为_______。
13
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
5、如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
26cm
6.如图所示,已知AB=AC,DE垂直平分AB交AC、AB于D、E两点,若AB=12cm,BC=l0cm,∠A=49°.求△BCD的周长和∠DBC度数。
我也行!
解:∵ DE垂直平分AB
∴AD=BD
∴∠A=∠1=49°
BD+CD=AD+CD=AC=AB=12cm
∵AB=AC,∠A= 49°
∴∠ABC=∠ACB=65.5 °
∴ ∠DBC= ∠ABC - ∠1=65.5-49=16.5 °
∴△BCD的周长为:BD+CD+BC=12+10=22cm
4:如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为_________
A
C
D
B
E
E
7:
如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,AC的距离相等.
┌
E
┕
D
F
┎
A
B
C
P
M
N
思考:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
8.如图,△ABC中,边AB、BC的垂直平分线交于点P。
(1)求证:PA=PB=PC。
(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
P
A
C
B
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
1.有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
作图题
6、有三条互相交叉的道路,要在三条道路围成的三角形区域内建一座加油站,使加油站的位置到三条路的距离相等,加油站应建在哪里呢? (如图)
L1
L2
L3
∴ OE=OF (等角对等边)
例2.如右图所示,已知,OC平分∠AOB,D是OC上一点,DE⊥OA,DF⊥OB,垂足为E、F点,那么 (1)∠DEF与∠DFE相等吗?为什么?
(2)OE与OF相等吗?为什么?
解:(1)相等。
理由: ∵ OC平分∠AOB, DE⊥OA,DF⊥OB(已知)
∴ DE=DF
∴∠1=∠2 (等边对等角)
(2)相等。
理由为:
∵ DE⊥OA,DF⊥OB
∴ ∠ 3= ∠ 4
∴ ∠ DEO=∠DFO=90 °
∵ ∠ 1= ∠ 2
∴ ∠ DEO - ∠ 1 =∠DFO - ∠ 2
变式:如图,E为∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D。求证:OE为CD的垂直平分线。
更上一层楼
如图,在△ABC中,∠ACB=90°,AD是角平分线,DE⊥AB于点E。
(1)AD是线段CE的垂直平分线吗?为什么?
(2)若△BDE的周长为13,EF=3,求△BCE的周长。
分析:由角平分线性质易得DE=DC,设法说明DA平分∠EDC,再根据“三线合一”说明AD是线段CE的垂直平分线。
顺藤摸瓜
解:(1)AD是线段CE的垂直平分线。
理由如下:
∵AD是三角形的角平分线,∠ACB=90°DE⊥AB.
∴DE=DC(角平分线上的点到角两边的距离相等)
∵∠3+∠1=∠4+∠2=90°(直角三角形的两锐角互余), ∠1=∠2
∴∠3=∠4,即DF平分∠EDC.
∴DF⊥CE并平分CE(等腰三角形的三线合一)
∴ AD是线段CE的垂直平分线。
(2)由(1)可知,DE=DC,EC=2EF=6,
∵△BDE的周长=EB+BD+DE=13,
∴EB+BD+DC=13,即EB+BC=13,
∴△BCE的周长=EB+BC+EC=13+6=19
等腰三角形和等边三角形专题
1、“有一个等腰三角形的两条边长分别是4cm和8cm,则周长为
20cm
2、若等腰三角形的一个角为400,则另外两个角的度数为
700,700 或 400,1000
3、已知,如图: AB=AC AD=DC=BC
则∠A=
A
B
C
D
360
4、已知,如图AB=AC=CD AD=BD
则∠BAC=
A
B
C
D
1080
5、如图,P、Q是△ABC边上的两点,BP=PQ=QC=AP=AQ,
求∠BAC的度数。
P
A
B
C
Q
6. (2010.宁波) 如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是△ABC、△BCD的角平分线, 则图中的等腰三角形有( )
A.5个 B.4个 C.3个 D.2个
A
7、下列四个说法中,不正确的有( )
(A)0个(B)1个(C)2个(D)3个
三个角都相等的三角形是等边三角形。
有两个角等于60°的三角形是等边三角形。
有一个是60°的等腰三角形是等边三角形。
有两个角相等的等腰三角形是等边三角形。
8、等边三角形的对称轴有( )
(A)1条(B)2条(C)3条(D)4条
B
C
大显身手
9.如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.
(1)、请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系;
∴∠2=∠ABO ∠3=∠ACO
O
A
B
C
E
F
若AB≠AC,其他条件不变,图中还有等腰三角形吗?(1)中结论还成立吗?
解:
EF=BE+CF
理由:
A
B
C
O
E
F
1
3
2
4
∵ EF∥BC
∴∠1=∠2 ∠3=∠4
∵ BO、CO分别平分∠ABC、∠ACB
∴∠1=∠ABO ∠4=∠ACO
∴BE=OE CF=OF
∵ EF=EO+FO
∴EF=BE+CF
10.已知:如图,线段CD垂直平分AB,AB平分?CAD. 求证:AD∥BC.
A
B
C
D
O
1
2
3
证明:
∵线段CD垂直平分AB(已知)
∴ CA=CB(线段垂直平分线的
性质定理)
∴ ? 1= ? 3(等边对等角)
又∵ AB平分?CAD(已知)
∴ ? 1= ? 2(角平分线的定义)
∴ ? 2= ? 3(等量代换)
∴ AD ∥BC(内错角相等,两直线平行)
例1
(1)
(2)若DE∥BC,交AB,AC于D,E.
△ADE是等边三角形吗?试说明理由。
11、已知,如图:△ABC中 AB=AC E为AC延长线上的一点且CE=BD DE交BC于F
求证:DF=EF
A
B
C
D
E
F
(提示:过D作DG∥AE交BC于G
证△DFG≌△EFC即可)
G
当堂过关
1.如果等腰三角形的一个底角为50°,那么其余两个角为______和_____.
2.如果等腰三角形的一角为80°,那么它的一个底角为___________________.
3.底角等于顶角一半的等腰三角形是______三角形.
4.等腰三角形的周长为16米,其中一条边的长是6,另两条边的长是 .
50°
80°
50°、50°或80°、20°
等边
6米、4米或5米、5米
7.在△ABC中,D是AC上的一点,且AB=AD,已知∠DBC+ ∠C=620,则∠ABD的大小关系是( )
A.670 B.620 C.600 D.560
8.若等腰三角形的周长为10,一边长为2,
则此等腰三角形的腰长为( )
A.2或4 B.4 C.3 D.2
9.如图,在△ABC中,DE是BC的
垂直平分线,垂足为点E,交AB于点D,若CE=5,△ABC的周长为25,则△ADC的周长为 。
B
B
15
10.下列图形中,不是轴对称图形的是( )
11.把一张长方形纸条折叠一次,EF是折痕,如果∠1=31°,那么∠2= 。
A
118 °
12.等边三角形的每一个内角均为 度。
60°
5.如图:请找出一点P,使点P到A,B两点的距离相等,并且点P在∠ACB的平分线上。
1.下列叙述中错误的是( )
A.一条线段有两条对称轴 B.一个角有一条对称轴
C.等腰三角形至少有一条对称轴 D.等腰三角形只有一条对称轴
2.我们称顶角为36 °的等腰三角形为“黄金三角形”。如图所示,现有一等腰△ABC,其中AB=AC,且∠ACB=2∠A, ∠ABC、∠ACB的角平分线BD、CE交于点O,如图中的“黄金三角形”共有( )
A.3 B.4 C.5 D.6
3.如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。
A
B
C
D
E
F
M
N
答:∠ MEF的度数=75 °
4.如图,已知线段BE是△ABC的角平分线,点D在边AB上,DE∥BC,
DB=DE吗?请说明理由;
(2)若点F是线段BE的中点,那么点F到∠BDE的两边的距离相等吗?请说明理由。
5.在△ABC中(如图),完成以下问题:
(1)作出△ABC的一个外角 ∠BCD,再作出是∠BCD的角平分线CE;
(2)若∠A=∠B,那么CE∥AB吗?说明你的理由。
13.如图,把一张长方形纸片ABCD对折,使点C落在E处与AD交于点O,请写出图中所有相等的线段。
复习方法
1.对整章的学习内容做一回顾,系统地把握全章的知识要点和基本技能。
2.通过例题和练习,能较好地运用本章知识和技能解决有关问题。
重点、难点
判断图形是否是轴对称图形,线段的垂直平分线、角平分线的性质、等腰三角形的性质和判定及其应用是学习重点,而灵活运用上述性质解决问题、轴对称图案的设计是学习难点。
本 章 知 识 结 构
生活中的对称
轴对称
轴对称图形的坐标特征
等边三角形的性质
等边三角形的判定
两个图形成轴对称
轴对称图形
等腰三角形的性质
等腰三角形的判定
等腰三角形
等边三角形
轴对称的性质
中垂线的性质与判定
画轴对称图形
应 用
轴对称的画法
一、知识要点回顾
记牢,别忘了哟!
1.一个图形沿某条直线对折,对折的两部分能 , 那么就称这样的图形为轴对称图形。 2.把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成 。 3.轴对称图形(或关于某条直线对称的两个图形)沿对称轴对折后的两部分是完全重合的,它的 相等, 相等.对称点的连线被对称轴 。4. 并且 一条线段的直线称为这条线段的垂直平分线。线段的垂直平分线上的点到这条线段两个端点的 。
5.角平分线上的点到角两边的距离 。
完全重合
轴对称
对应线段
对应角
垂直平分
垂直
平分
距离相等
相等
6.等腰三角形底边的中线、高线、顶角的平分线 ,等腰三角形的 相等(等边对等角),等边三角形的三个角都等于 °
7.如果一个三角形有两个角相等,那么这两个角所对的边 (等角对等边);有两个角是60°的三角形是 三角形,有一个角是 °的等腰三角形是等边三角形。
互相重合
两个底角
60
也相等
60
等边
记牢,别忘了哟!
轴对称专题
常见的轴对称图形
名称
常见的轴对称图形
对称轴条数
对称轴
角
线段
等腰三角形
等边三角形
圆
正方形
长方形
菱形
等腰梯形
角平分线所在的直线
2
线段的垂直平分线和线段所在的直线
1
等腰三角形底边上的高所在的直线
3
等边三角形各边上的高所在的直线
无数条
过圆心的任意一条直线
4
两条对角线所在的直线以及两组对边中点所在的直线
2
两组对边中点所在的直线
2
两条对角线所在的直线
1
上、下底边中点所在的直线
1
常在选择题、填空题中出现
二、例题精选
例1.下列图案是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
B
举一反三:1、在下列图形中,是轴对称图形的是( )
A、锐角三角形 B、曲线 C、线段 D、直角三角形
2、等腰三角形的对称轴有( )A、一条 B、二条
C、三条 D、一条或三条
3、下列图形中不是轴对称图形的是( )
A、有两个角相等的三角形 B、有一角为45°的直角三角形?
C、有两个角分别为50°与80°的三角形
D、有两个角分别为55°与65°的三角形
C
D
D
如图,∠AOB内一点P,P1P2分别为P关于OA,OB的对称点, P1P2交OA于M,交OB于N,若P1P2 =5cm,求△PMN的周长。
用坐标表示轴对称小结:
在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(x, - y)
(- x, y)
1、完成下表.
已知点
(2,-3)
(-1,2)
(-6,-5)
(0,-1.6)
(4,0)
关于x轴的对称点
关于y轴的对称点
(-2, -3)
(2, 3)
(-1,-2)
(1, 2)
(6, -5)
(-6, 5)
(0, -1.6)
(0,1.6)
(-4,0)
(4,0)
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
练 习
2
4
6
-20
(抢答)
垂直平分线和角平分线专题
基础闯关
1、如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED= cm;如果∠ECD=600,那么∠EDC= 0.
E
D
A
B
C
7
60
2、如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____.
A
B
E
D
C
(1)
4
6
基础闯关
3、已知如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长为_______。
13
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
5、如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
26cm
6.如图所示,已知AB=AC,DE垂直平分AB交AC、AB于D、E两点,若AB=12cm,BC=l0cm,∠A=49°.求△BCD的周长和∠DBC度数。
我也行!
解:∵ DE垂直平分AB
∴AD=BD
∴∠A=∠1=49°
BD+CD=AD+CD=AC=AB=12cm
∵AB=AC,∠A= 49°
∴∠ABC=∠ACB=65.5 °
∴ ∠DBC= ∠ABC - ∠1=65.5-49=16.5 °
∴△BCD的周长为:BD+CD+BC=12+10=22cm
4:如图,在△ABC中,∠C=900,AD平分∠BAC交BC于点D,若BC=8,BD=5,则点D到AB的距离为_________
A
C
D
B
E
E
7:
如图,△ABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,AC的距离相等.
┌
E
┕
D
F
┎
A
B
C
P
M
N
思考:点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
8.如图,△ABC中,边AB、BC的垂直平分线交于点P。
(1)求证:PA=PB=PC。
(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
P
A
C
B
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
1.有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
作图题
6、有三条互相交叉的道路,要在三条道路围成的三角形区域内建一座加油站,使加油站的位置到三条路的距离相等,加油站应建在哪里呢? (如图)
L1
L2
L3
∴ OE=OF (等角对等边)
例2.如右图所示,已知,OC平分∠AOB,D是OC上一点,DE⊥OA,DF⊥OB,垂足为E、F点,那么 (1)∠DEF与∠DFE相等吗?为什么?
(2)OE与OF相等吗?为什么?
解:(1)相等。
理由: ∵ OC平分∠AOB, DE⊥OA,DF⊥OB(已知)
∴ DE=DF
∴∠1=∠2 (等边对等角)
(2)相等。
理由为:
∵ DE⊥OA,DF⊥OB
∴ ∠ 3= ∠ 4
∴ ∠ DEO=∠DFO=90 °
∵ ∠ 1= ∠ 2
∴ ∠ DEO - ∠ 1 =∠DFO - ∠ 2
变式:如图,E为∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D。求证:OE为CD的垂直平分线。
更上一层楼
如图,在△ABC中,∠ACB=90°,AD是角平分线,DE⊥AB于点E。
(1)AD是线段CE的垂直平分线吗?为什么?
(2)若△BDE的周长为13,EF=3,求△BCE的周长。
分析:由角平分线性质易得DE=DC,设法说明DA平分∠EDC,再根据“三线合一”说明AD是线段CE的垂直平分线。
顺藤摸瓜
解:(1)AD是线段CE的垂直平分线。
理由如下:
∵AD是三角形的角平分线,∠ACB=90°DE⊥AB.
∴DE=DC(角平分线上的点到角两边的距离相等)
∵∠3+∠1=∠4+∠2=90°(直角三角形的两锐角互余), ∠1=∠2
∴∠3=∠4,即DF平分∠EDC.
∴DF⊥CE并平分CE(等腰三角形的三线合一)
∴ AD是线段CE的垂直平分线。
(2)由(1)可知,DE=DC,EC=2EF=6,
∵△BDE的周长=EB+BD+DE=13,
∴EB+BD+DC=13,即EB+BC=13,
∴△BCE的周长=EB+BC+EC=13+6=19
等腰三角形和等边三角形专题
1、“有一个等腰三角形的两条边长分别是4cm和8cm,则周长为
20cm
2、若等腰三角形的一个角为400,则另外两个角的度数为
700,700 或 400,1000
3、已知,如图: AB=AC AD=DC=BC
则∠A=
A
B
C
D
360
4、已知,如图AB=AC=CD AD=BD
则∠BAC=
A
B
C
D
1080
5、如图,P、Q是△ABC边上的两点,BP=PQ=QC=AP=AQ,
求∠BAC的度数。
P
A
B
C
Q
6. (2010.宁波) 如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是△ABC、△BCD的角平分线, 则图中的等腰三角形有( )
A.5个 B.4个 C.3个 D.2个
A
7、下列四个说法中,不正确的有( )
(A)0个(B)1个(C)2个(D)3个
三个角都相等的三角形是等边三角形。
有两个角等于60°的三角形是等边三角形。
有一个是60°的等腰三角形是等边三角形。
有两个角相等的等腰三角形是等边三角形。
8、等边三角形的对称轴有( )
(A)1条(B)2条(C)3条(D)4条
B
C
大显身手
9.如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.
(1)、请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系;
∴∠2=∠ABO ∠3=∠ACO
O
A
B
C
E
F
若AB≠AC,其他条件不变,图中还有等腰三角形吗?(1)中结论还成立吗?
解:
EF=BE+CF
理由:
A
B
C
O
E
F
1
3
2
4
∵ EF∥BC
∴∠1=∠2 ∠3=∠4
∵ BO、CO分别平分∠ABC、∠ACB
∴∠1=∠ABO ∠4=∠ACO
∴BE=OE CF=OF
∵ EF=EO+FO
∴EF=BE+CF
10.已知:如图,线段CD垂直平分AB,AB平分?CAD. 求证:AD∥BC.
A
B
C
D
O
1
2
3
证明:
∵线段CD垂直平分AB(已知)
∴ CA=CB(线段垂直平分线的
性质定理)
∴ ? 1= ? 3(等边对等角)
又∵ AB平分?CAD(已知)
∴ ? 1= ? 2(角平分线的定义)
∴ ? 2= ? 3(等量代换)
∴ AD ∥BC(内错角相等,两直线平行)
例1
(1)
(2)若DE∥BC,交AB,AC于D,E.
△ADE是等边三角形吗?试说明理由。
11、已知,如图:△ABC中 AB=AC E为AC延长线上的一点且CE=BD DE交BC于F
求证:DF=EF
A
B
C
D
E
F
(提示:过D作DG∥AE交BC于G
证△DFG≌△EFC即可)
G
当堂过关
1.如果等腰三角形的一个底角为50°,那么其余两个角为______和_____.
2.如果等腰三角形的一角为80°,那么它的一个底角为___________________.
3.底角等于顶角一半的等腰三角形是______三角形.
4.等腰三角形的周长为16米,其中一条边的长是6,另两条边的长是 .
50°
80°
50°、50°或80°、20°
等边
6米、4米或5米、5米
7.在△ABC中,D是AC上的一点,且AB=AD,已知∠DBC+ ∠C=620,则∠ABD的大小关系是( )
A.670 B.620 C.600 D.560
8.若等腰三角形的周长为10,一边长为2,
则此等腰三角形的腰长为( )
A.2或4 B.4 C.3 D.2
9.如图,在△ABC中,DE是BC的
垂直平分线,垂足为点E,交AB于点D,若CE=5,△ABC的周长为25,则△ADC的周长为 。
B
B
15
10.下列图形中,不是轴对称图形的是( )
11.把一张长方形纸条折叠一次,EF是折痕,如果∠1=31°,那么∠2= 。
A
118 °
12.等边三角形的每一个内角均为 度。
60°
5.如图:请找出一点P,使点P到A,B两点的距离相等,并且点P在∠ACB的平分线上。
1.下列叙述中错误的是( )
A.一条线段有两条对称轴 B.一个角有一条对称轴
C.等腰三角形至少有一条对称轴 D.等腰三角形只有一条对称轴
2.我们称顶角为36 °的等腰三角形为“黄金三角形”。如图所示,现有一等腰△ABC,其中AB=AC,且∠ACB=2∠A, ∠ABC、∠ACB的角平分线BD、CE交于点O,如图中的“黄金三角形”共有( )
A.3 B.4 C.5 D.6
3.如图:点B、C、D、E、F在∠MAN的边上, ∠A=15°,AB=BC=CD=DE=EF,求∠ MEF的度数。
A
B
C
D
E
F
M
N
答:∠ MEF的度数=75 °
4.如图,已知线段BE是△ABC的角平分线,点D在边AB上,DE∥BC,
DB=DE吗?请说明理由;
(2)若点F是线段BE的中点,那么点F到∠BDE的两边的距离相等吗?请说明理由。
5.在△ABC中(如图),完成以下问题:
(1)作出△ABC的一个外角 ∠BCD,再作出是∠BCD的角平分线CE;
(2)若∠A=∠B,那么CE∥AB吗?说明你的理由。
13.如图,把一张长方形纸片ABCD对折,使点C落在E处与AD交于点O,请写出图中所有相等的线段。
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
