初中数学人教版八年级上册第14章 整式乘法与因式分解 14.1.4 整式的除法 课件(共23张ppt)
文档属性
| 名称 | 初中数学人教版八年级上册第14章 整式乘法与因式分解 14.1.4 整式的除法 课件(共23张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:41:18 | ||
图片预览







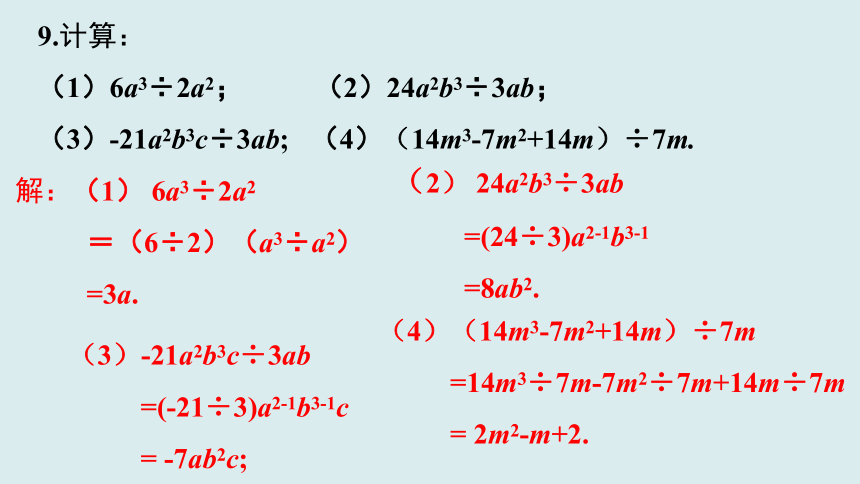

文档简介
整式的除法
一般地,我们有
am ÷an=am-n (a ≠0,m,n都是正整数,且m>n)
即 同底数幂相除,底数不变,指数相减.
精彩点拨
同底数幂的除法
想一想:am÷am=? (a≠0)
答:am÷am=1,根据同底数幂的除法法则可得am÷am=a0.
a0 =1(a ≠0)
这就是说,任何不等于0的数的0次幂都等于1.
1.同底数幂的除法法则:am÷an=____(a≠0,m,n都是正整数,并且m>n).即同底数幂相除,__________,__________.
2.a0=____(a≠0).即任何不等于0的数的0次幂都等于____.
3.单项式相除,把____与_________分别相除作为商的____,对于只在被除式里含有的字母,则_______________作为商的一个因式.
4.多项式除以单项式,先把这个多项式的______都除以_____________,再把所得的商____.
am-n
底数不变
指数相减
1
1
系数
同底数幂
因式
连同它的指数
每一项
这个单项式
相加
基础检测
2.下列算式中,不正确的是( )
A.(-12a5b)÷(-3ab)=4a4 B.9xmyn-1÷3xm-2yn-3=3x2y2
C.4a2b3÷2ab=2ab2 D.x(x-y)2÷(y-x)=x(x-y)
1.下列说法正确的是 ( )
A.(π-3.14)0没有意义 B.任何数的0次幂都等于1
C.(8×106)÷(2×109)=4×103 D.若(x+4)0=1,则x≠-4
D
D
3.(2分)(安徽中考)计算a10÷a2(a≠0)的结果是( )
A.a5 B.a-5 C.a8 D.a-8
4.(2分)(2017·盐城)下列运算中,正确的是( )
A.7a+a=7a2 B.a2·a3=a6
C.a3÷a=a2 D.(ab)2=ab2
5.(3分)若7m-3n=2,则107m÷103n=____.
C
C
100
8. 已知一多项式与单项式-7x5y4 的积为21x5y7-28x6y5,则这个多项式是 .
-3y3+4xy
7.一个长方形的面积为a2+2a,若一边长为a,则另一边长为_____________.
a+2
6.已知28a3bm÷28anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3
A
解:(1)x5
解:(3)a2b2
(4)x-y
9.计算:
(1)6a3÷2a2; (2)24a2b3÷3ab;
(3)-21a2b3c÷3ab; (4)(14m3-7m2+14m)÷7m.
解:(1) 6a3÷2a2
=(6÷2)(a3÷a2)
=3a.
(2) 24a2b3÷3ab
=(24÷3)a2-1b3-1
=8ab2.
(3)-21a2b3c÷3ab
=(-21÷3)a2-1b3-1c
= -7ab2c;
(4)(14m3-7m2+14m)÷7m
=14m3÷7m-7m2÷7m+14m÷7m
= 2m2-m+2.
1
A
4xy
C
9. 计算(12a3-6a2+3a) ÷3a.
解: (12a3-6a2+3a) ÷3a
=12a3÷3a+(-6a2) ÷3a+3a÷3a
=4a2+(-2a)+1
=4a2-2a+1.
B
11.计算:(1)(6x3y4z-4x2y3z+2xy3)÷2xy3;
(2)(72x3y4-36x2y3+9xy2)÷(-9xy2).
(2)原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)
+9xy2÷(-9xy2)
=-8x2y2+4xy-1.
解:(1)原式=6x3y4z÷2xy3-4x2y3z÷2xy3+2xy3÷2xy3
=3x2yz-2xz+1;
解:原式=-3x2+2x-1
解:原式=-6+4xy+2x2y2
13.(8分)计算:
(1)(-a)8÷(-a5); (2)(x-y)7÷(y-x)6;
解:(1)-a3
(3)(-m4)3÷(-m)7; (4)x7÷(x5÷x3).
解:(3)m5
(2)x-y
(4)x5
12 先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2015,y=2014.
原式=x-y=2015-2014=1.
=x-y.
把x=2015,y=2014代入上式,得
解:原式=[2x3y-2x2y2+x2y2-x3y]÷x2y,
14.先化简,再求值:(x+y)(x-y)-(4x3y-8xy3)÷2xy,其中x=1,y=-3.
解:原式=x2-y2-2x2+4y2
原式=-12+3×(-3)2=-1+27=26.
当x=1,y=-3时,
=-x2+3y2.
解:x-3
20.(8分)先化简,再求值:(4ab3-8a2b2)÷4ab+(2a+b)(2a-b),
其中a=2,b=1.
解:原式=4a2-2ab,当a=2,b=1时,原式=16-4=12
15.(1)若32?92x+1÷27x+1=81,求x的值;
解:(1)32?34x+2÷33x+3=81,
即 3x+1=34,
解得x=3;
(2) 已知5x=36,5y=2,求5x-2y的值;
(2)52y=(5y)2=4,
5x-2y=5x÷52y=36÷4=9.
拓展提升
(3)已知2x-5y-4=0,求4x÷32y的值.
解 (3) ∵2x-5y-4=0,
移项 2x-5y=4.
4x÷32y
= 22x÷25y
=22x-5y
=24
=16.
一般地,我们有
am ÷an=am-n (a ≠0,m,n都是正整数,且m>n)
即 同底数幂相除,底数不变,指数相减.
精彩点拨
同底数幂的除法
想一想:am÷am=? (a≠0)
答:am÷am=1,根据同底数幂的除法法则可得am÷am=a0.
a0 =1(a ≠0)
这就是说,任何不等于0的数的0次幂都等于1.
1.同底数幂的除法法则:am÷an=____(a≠0,m,n都是正整数,并且m>n).即同底数幂相除,__________,__________.
2.a0=____(a≠0).即任何不等于0的数的0次幂都等于____.
3.单项式相除,把____与_________分别相除作为商的____,对于只在被除式里含有的字母,则_______________作为商的一个因式.
4.多项式除以单项式,先把这个多项式的______都除以_____________,再把所得的商____.
am-n
底数不变
指数相减
1
1
系数
同底数幂
因式
连同它的指数
每一项
这个单项式
相加
基础检测
2.下列算式中,不正确的是( )
A.(-12a5b)÷(-3ab)=4a4 B.9xmyn-1÷3xm-2yn-3=3x2y2
C.4a2b3÷2ab=2ab2 D.x(x-y)2÷(y-x)=x(x-y)
1.下列说法正确的是 ( )
A.(π-3.14)0没有意义 B.任何数的0次幂都等于1
C.(8×106)÷(2×109)=4×103 D.若(x+4)0=1,则x≠-4
D
D
3.(2分)(安徽中考)计算a10÷a2(a≠0)的结果是( )
A.a5 B.a-5 C.a8 D.a-8
4.(2分)(2017·盐城)下列运算中,正确的是( )
A.7a+a=7a2 B.a2·a3=a6
C.a3÷a=a2 D.(ab)2=ab2
5.(3分)若7m-3n=2,则107m÷103n=____.
C
C
100
8. 已知一多项式与单项式-7x5y4 的积为21x5y7-28x6y5,则这个多项式是 .
-3y3+4xy
7.一个长方形的面积为a2+2a,若一边长为a,则另一边长为_____________.
a+2
6.已知28a3bm÷28anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3
A
解:(1)x5
解:(3)a2b2
(4)x-y
9.计算:
(1)6a3÷2a2; (2)24a2b3÷3ab;
(3)-21a2b3c÷3ab; (4)(14m3-7m2+14m)÷7m.
解:(1) 6a3÷2a2
=(6÷2)(a3÷a2)
=3a.
(2) 24a2b3÷3ab
=(24÷3)a2-1b3-1
=8ab2.
(3)-21a2b3c÷3ab
=(-21÷3)a2-1b3-1c
= -7ab2c;
(4)(14m3-7m2+14m)÷7m
=14m3÷7m-7m2÷7m+14m÷7m
= 2m2-m+2.
1
A
4xy
C
9. 计算(12a3-6a2+3a) ÷3a.
解: (12a3-6a2+3a) ÷3a
=12a3÷3a+(-6a2) ÷3a+3a÷3a
=4a2+(-2a)+1
=4a2-2a+1.
B
11.计算:(1)(6x3y4z-4x2y3z+2xy3)÷2xy3;
(2)(72x3y4-36x2y3+9xy2)÷(-9xy2).
(2)原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)
+9xy2÷(-9xy2)
=-8x2y2+4xy-1.
解:(1)原式=6x3y4z÷2xy3-4x2y3z÷2xy3+2xy3÷2xy3
=3x2yz-2xz+1;
解:原式=-3x2+2x-1
解:原式=-6+4xy+2x2y2
13.(8分)计算:
(1)(-a)8÷(-a5); (2)(x-y)7÷(y-x)6;
解:(1)-a3
(3)(-m4)3÷(-m)7; (4)x7÷(x5÷x3).
解:(3)m5
(2)x-y
(4)x5
12 先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2015,y=2014.
原式=x-y=2015-2014=1.
=x-y.
把x=2015,y=2014代入上式,得
解:原式=[2x3y-2x2y2+x2y2-x3y]÷x2y,
14.先化简,再求值:(x+y)(x-y)-(4x3y-8xy3)÷2xy,其中x=1,y=-3.
解:原式=x2-y2-2x2+4y2
原式=-12+3×(-3)2=-1+27=26.
当x=1,y=-3时,
=-x2+3y2.
解:x-3
20.(8分)先化简,再求值:(4ab3-8a2b2)÷4ab+(2a+b)(2a-b),
其中a=2,b=1.
解:原式=4a2-2ab,当a=2,b=1时,原式=16-4=12
15.(1)若32?92x+1÷27x+1=81,求x的值;
解:(1)32?34x+2÷33x+3=81,
即 3x+1=34,
解得x=3;
(2) 已知5x=36,5y=2,求5x-2y的值;
(2)52y=(5y)2=4,
5x-2y=5x÷52y=36÷4=9.
拓展提升
(3)已知2x-5y-4=0,求4x÷32y的值.
解 (3) ∵2x-5y-4=0,
移项 2x-5y=4.
4x÷32y
= 22x÷25y
=22x-5y
=24
=16.
