华东师大版八年级上册数学第12章 整式的乘除 复习课件(共22张ppt)
文档属性
| 名称 | 华东师大版八年级上册数学第12章 整式的乘除 复习课件(共22张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 451.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:51:13 | ||
图片预览








文档简介
(共22张PPT)
整式的乘除
复习课
重难点知识归纳
重点 整式的乘除法,乘法公式的应用
难点 整式乘法公式的应用 · 因式分解
要突破上述难点,先要认真掌握好乘法公式的基本结构,再要针对性地加强练习,以达到熟练自如的目的。
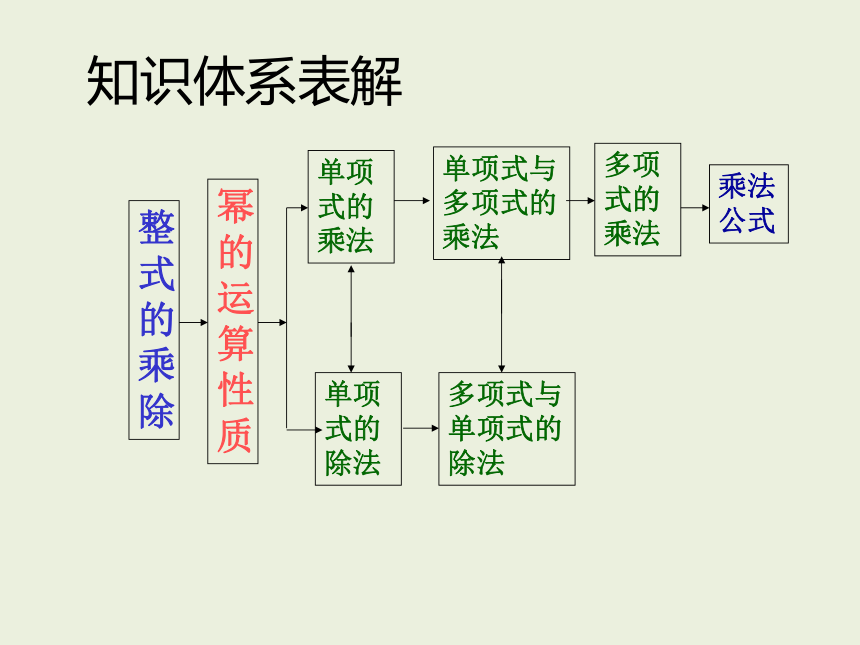
知识表解
幂的运算性质
整式的乘除
单项式与多项式的乘法
单项式的乘法
多项式的乘法
乘法公式
单项式的除法
多项式与单项式的除法
知识体系表解
同底数幂的乘法
am an=am+n (m、n都是正整数)
(am)n=amn (m、n都是正整数)
幂的乘方
积的乘方
(ab)=an bn (n是正整数)
同底数幂的除法
am ÷an=am-n
(a≠0,m、n都是正整数,m>n)
2、a0=1,(a≠0 )
3、
1、
单项式乘法
单项式相乘,把它们的系数、
相同字母分别相乘,对于只在一
个单项式里出现的字母,则连同
它的指数作为积的一个因式。
多项式乘以单项式
多项式乘以单项式,用
单项式去乘以多项式的每一
项,并把所得的 积 相加。
多项式乘以多项式
多项式乘以多项式,用一
个多项式的每一项去乘以另一
个多项式的每一项,并把所得
的 积 相加。
乘法公式
(x+a)(x+b)=x2+(a+b)x+ab
(a+b)(a-b)=a2-b2
(a±b) =a2± 2ab+b2
单项式的除法
单项式相除,把它们的系数、
同底数幂分别相除,作为商的一
个因式,对于只在被除式里含有
的字母,则连同它的指数作为商
的一个因式。
多项式除以单项式
多项式除以单项式,先
把这个多项式的每一项除以
这个单项式,再把所得的商
相加。
一、判断正误:
A.b5 b5=2b5( ) B.x5+x5=x10 ( )
C.(c3)4 ÷c5=c6 ( )
D.(m3 m2)5÷m4=m21 ( )
二、计算(口答)
1.(-3)2 (-3)3=
2. x3 xn-1-xn-2 x4+xn+2=
3.(m-n)2 (n-m)2 (n-m)3=
4. -(- 2a2b4)3=
5.(-2ab)3 b5 ÷8a2b4=
-35
xn+2
(n-m)3
-ab4
8a6b12
(-3)5
=
小结:
1.底是否一致
2.注意符号
例1:计算:
典型例题:
例2:
例2:
小结:
1.变换指数
2.变换底数
求证不论x、y取何值,代数式 x2+y2+4x-6y+14的值总是正数。
即原式的值总是正数
证明:
x2+y2+4x-6y+14
= x2+ 4x + 4+y2-6y+9+1
=(x+2)2+(y-3)2+1
∵ (x+2)2≥0,(y-3)2 ≥0
∴ (x+2)2+(y-3)2+1>0
若10a=20,10b=5-1,求9a÷32b的值。
解:∵ 10a ÷ 10b=10a-b
∴10a-b=20 ÷ 5-1=100=102
∴ a-b=2
∵ 9a÷32b= 9a ÷ 9b=9a-b
∴ 9a÷32b= 92=81
思考题
1、观察下列各式:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
根据前面各式的规律可得
(x-1)(xn+xn-1+ +x+1)=____ (其中n为正整数)
xn+1-1
因式分解的概念
一个多项式→几个整式的积→因式分解
要注意的问题:
(1)因式分解是对多项式而言的一种变形;
(2)因式分解的结果仍是整式;
(3)因式分解的结果必是一个积;
(4)因式分解与整式乘法正好相反。
1.公因式
一个多项式中的每一项都含有的相同的因式,称之为公因式(common factor)。
2.提公因式法
一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种因式分解的方法叫做提公因式法。如 ma+mb+mc=m(a+b+c)
公式法 将乘法公式反过来应用,就可以把某些多项式分解因式,这种分解因式的方法,叫做公式法。
例1对下列多项式进行因式分解:
(1)-5a2+25a; (2)3a2-9ab;
(3)25x2-16y2; (4)x2+4xy+4y2.
例2 对下列多项式进行因式分解:
(1)4x3y+4x2y2+xy3;
(2)3x3-12xy2
例2、分解因式
解:原式
练习:
整式的乘除
复习课
重难点知识归纳
重点 整式的乘除法,乘法公式的应用
难点 整式乘法公式的应用 · 因式分解
要突破上述难点,先要认真掌握好乘法公式的基本结构,再要针对性地加强练习,以达到熟练自如的目的。
知识表解
幂的运算性质
整式的乘除
单项式与多项式的乘法
单项式的乘法
多项式的乘法
乘法公式
单项式的除法
多项式与单项式的除法
知识体系表解
同底数幂的乘法
am an=am+n (m、n都是正整数)
(am)n=amn (m、n都是正整数)
幂的乘方
积的乘方
(ab)=an bn (n是正整数)
同底数幂的除法
am ÷an=am-n
(a≠0,m、n都是正整数,m>n)
2、a0=1,(a≠0 )
3、
1、
单项式乘法
单项式相乘,把它们的系数、
相同字母分别相乘,对于只在一
个单项式里出现的字母,则连同
它的指数作为积的一个因式。
多项式乘以单项式
多项式乘以单项式,用
单项式去乘以多项式的每一
项,并把所得的 积 相加。
多项式乘以多项式
多项式乘以多项式,用一
个多项式的每一项去乘以另一
个多项式的每一项,并把所得
的 积 相加。
乘法公式
(x+a)(x+b)=x2+(a+b)x+ab
(a+b)(a-b)=a2-b2
(a±b) =a2± 2ab+b2
单项式的除法
单项式相除,把它们的系数、
同底数幂分别相除,作为商的一
个因式,对于只在被除式里含有
的字母,则连同它的指数作为商
的一个因式。
多项式除以单项式
多项式除以单项式,先
把这个多项式的每一项除以
这个单项式,再把所得的商
相加。
一、判断正误:
A.b5 b5=2b5( ) B.x5+x5=x10 ( )
C.(c3)4 ÷c5=c6 ( )
D.(m3 m2)5÷m4=m21 ( )
二、计算(口答)
1.(-3)2 (-3)3=
2. x3 xn-1-xn-2 x4+xn+2=
3.(m-n)2 (n-m)2 (n-m)3=
4. -(- 2a2b4)3=
5.(-2ab)3 b5 ÷8a2b4=
-35
xn+2
(n-m)3
-ab4
8a6b12
(-3)5
=
小结:
1.底是否一致
2.注意符号
例1:计算:
典型例题:
例2:
例2:
小结:
1.变换指数
2.变换底数
求证不论x、y取何值,代数式 x2+y2+4x-6y+14的值总是正数。
即原式的值总是正数
证明:
x2+y2+4x-6y+14
= x2+ 4x + 4+y2-6y+9+1
=(x+2)2+(y-3)2+1
∵ (x+2)2≥0,(y-3)2 ≥0
∴ (x+2)2+(y-3)2+1>0
若10a=20,10b=5-1,求9a÷32b的值。
解:∵ 10a ÷ 10b=10a-b
∴10a-b=20 ÷ 5-1=100=102
∴ a-b=2
∵ 9a÷32b= 9a ÷ 9b=9a-b
∴ 9a÷32b= 92=81
思考题
1、观察下列各式:
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
根据前面各式的规律可得
(x-1)(xn+xn-1+ +x+1)=____ (其中n为正整数)
xn+1-1
因式分解的概念
一个多项式→几个整式的积→因式分解
要注意的问题:
(1)因式分解是对多项式而言的一种变形;
(2)因式分解的结果仍是整式;
(3)因式分解的结果必是一个积;
(4)因式分解与整式乘法正好相反。
1.公因式
一个多项式中的每一项都含有的相同的因式,称之为公因式(common factor)。
2.提公因式法
一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种因式分解的方法叫做提公因式法。如 ma+mb+mc=m(a+b+c)
公式法 将乘法公式反过来应用,就可以把某些多项式分解因式,这种分解因式的方法,叫做公式法。
例1对下列多项式进行因式分解:
(1)-5a2+25a; (2)3a2-9ab;
(3)25x2-16y2; (4)x2+4xy+4y2.
例2 对下列多项式进行因式分解:
(1)4x3y+4x2y2+xy3;
(2)3x3-12xy2
例2、分解因式
解:原式
练习:
