青岛版数学九年级下册课件5.5确定二次函数的表达式(共28张PPT)
文档属性
| 名称 | 青岛版数学九年级下册课件5.5确定二次函数的表达式(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 288.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 22:07:01 | ||
图片预览








文档简介
确定二次函数的表达式
用待定系数法求二次函数的解析式
一、一般式:y=ax?+bx+c (a,b,c为常数,a ≠0)
求二次函数y=ax2+bx+c的解析式,关键是求出待定系数a,b,c的值。
由已知条件(如二次函数图像上三个点的坐标)列出关于a,b,c的方程组,并求出a,b,c,就可以写出二次函数的解析式。
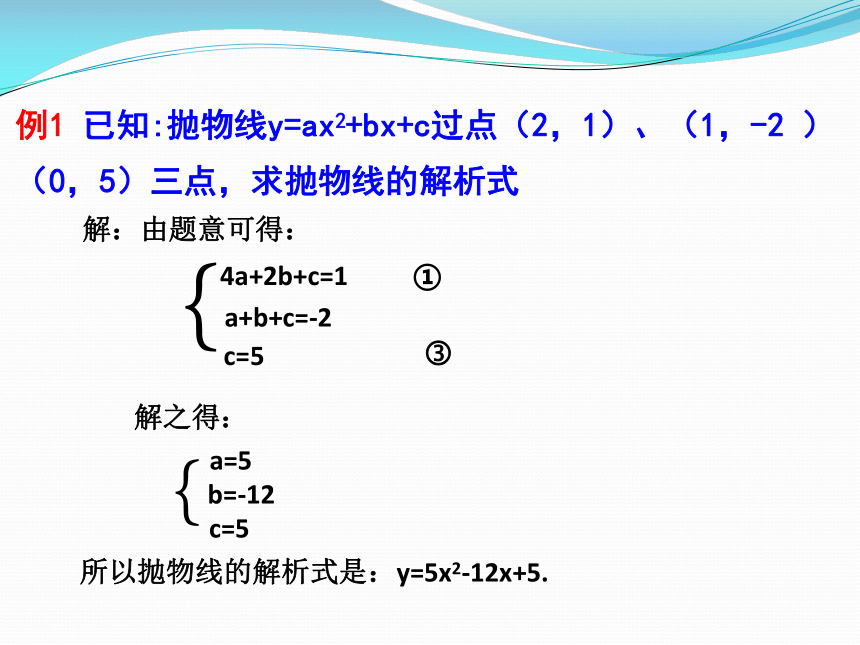
例1 已知:抛物线y=ax2+bx+c过点(2,1)、(1,-2 )(0,5)三点,求抛物线的解析式
解:由题意可得:
{
4a+2b+c=1 ①
a+b+c=-2 ?
c=5 ?
解之得:
{
a=5
b=-12
c=5
所以抛物线的解析式是:y=5x2-12x+5.
练
已知一个二次函数的图象过点(-1,10)、
(1,4)、(2,7)三点,求这个函数的表达式?
o
x
y
解:
设所求的二次函数为 y=ax2+bx+c
由条件得:
a-b+c=10
a+b+c=4
4a+2b+c=7
解方程得:
a=2, b=-3, c=5
所以所求二次函数是:
y=2x2-3x+5
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
二、顶点式y=a(x-h)2+k(a、h、k为常数a≠0).
1.若已知抛物线的顶点坐标和抛物线上的另一个点的坐标时,通过设函数的解析式为顶点式y=a(x-h)2+k.
2. 特别地,当抛物线的顶点为原点是,h=0,k=0,可设函数的解析式为y=ax2.
3.当抛物线的对称轴为y轴时,h=0,可设函数的解析式为y=ax2+k.
4.当抛物线的顶点在x轴上时,k=0,可设函数的解析式为y=a(x-h)2.
解:
1.已知抛物线的顶点为(-1,-3),与y轴交点为(0,-5),求该抛物线的解析式?
y
o
x
所以设所求的二次函数解析式为:y=a(x+1)2-3
因为已知抛物线的顶点为(-1,-3)
又点( 0,-5 )在抛物线上
a-3=-5, 解得a= -2
故所求的抛物线解析式为 y=-2(x+1)2-3
即:y=-2x2-4x-5
2. 已知一个二次函数的图象经过点(4,-3),并且当x=3时有最大值4,试确定这个二次函数的解析式。
解法1:(利用一般式)
设二次函数解析式为:y=ax2+bx+c (a≠0)
由题意知 16a+4b+c = -3
?????? -b/2a = 3
???? (4ac-b2)/4a = 4
解方程组得:?
a= -7
b= 42
c= -59
∴?二次函数的解析式为:y= -7x2+42x-59?
解法2:(利用顶点式)
∵? 当x=3时,有最大值4∴? 顶点坐标为(3,4)
设二次函数解析式为:y=a(x-3)2+4
∵? 函数图象过点(4,- 3)
∴? a(4 - 3)2 +4 = - 3
∴? a= -7
∴?二次函数的解析式为:
y= -7(x-3)2+4
3.二次函数y=ax2+bx+c的图象过点A(0,5), B(5,0)两点,它的对称轴为直线x=3,求这个二次函数的解析式。
解: ∵ 二次函数的对称轴为直线x=3
∴设二次函数表达式为 ? y=a(x-3)2+k
图象过点A(0,5),B(5,0)两点
∴ 5=a(0-3)2+k
0=a(5-3)2+k
解得:a= 1 k=-4
∴?二次函数的表达式: y= (x-3)2-4
即 ? y =x2-6x+5
小结:
已知顶点坐标(h,k)或对称轴方程x=h时优先选用顶点式。
三、交点式y=a(x-x1)(x-x2).(a、x1、x2为常数a≠0)
当抛物线与x轴有两个交点为(x1,0),(x2,0)时,二次函数y=ax2+bx+c可以转化为交点式y=a(x-x1)(x-x2).因此当抛物线与x轴有两个交点为(x1,0),(x2,0)时,可设函数的解析式为y=a(x-x1)(x-x2),在把另一个点的坐标代入其中,即可解得a,求出抛物线的解析式。
交点式y=a(x-x1)(x-x2). x1和x2分别是抛物线与x轴的两个交点的横坐标,这两个交点关于抛物线的对称轴对称,则直线 就是抛物线的对称轴.
1:已知二次函数与x 轴的交点坐标为(-1,0),(1,0),点(0,1)在图像上,求其解析式。
解:设所求的解析式为
∵抛物线与x轴的交点坐标为(-1,0)、(1,0)
∴
又∵点(0,1)在图像上,
∴ a = -1
即:
∴
∴
∴
解:(交点式)
∵二次函数图象经过点 (3,0),(-1,0)
∴设二次函数表达式为 :y=a(x-3)(x+1)
∵ 函数图象过点(1,4)
∴ 4 =a (1-3)(1+1) 得 a= -1
∴ 函数的表达式为:
?y= -(x+1)(x-3)
= -x2+2x+3
2:已知二次函数图象经过点 (1,4),(-1,0)和(3,0)三点,求二次函数的表达式。
知道抛物线与x轴的两个交点的坐标,选用交点式比较简便
其它解法:(一般式)
设二次函数解析式为y=ax2+bx+c
∵二次函数图象过点(1,4),(-1,0)和(3,0)
∴? a+b+c=4?????? ①
??? a-b+c=0?????? ②
?? 9a+3b+c=0??? ? ③
? 解得: a= -1
b=2
c=3
?∴? 函数的解析式为:y= -x2+2x+3
(顶点式)
解:
∵? 抛物线与x轴相交两点(-1,0)和(3,0) ,
∴ (-1+3)/2 = 1
∴? 点(1,4)为抛物线的顶点
可设二次函数解析式为: y=a(x-1)2+4?
∵ 抛物线过点(-1, 0)
∴ 0=a(-1-1)2+4 得 a= -1
∴ 函数的解析式为:
y= -(x-1)2+4
3 已知二次函数的图象在x轴上截得的线段长是4,且当x=1,函数有最小值-4,求这个二次函数的解析式.
(-1, 0)
(3, 0)
X=1
由题意,得:
解:设图象与x轴的交点坐标为
( ,0),( ,0),
把(1,-4)代入上式得:-4=a(1-3)(1+1)
解得:a=1
∴y=x2-2x-3
四、用平移式求二次函数的解析式、
1.将抛物线 向左平移4个单位,再向下平移3个单位,求平移后所得抛物线的解析式。
解法:将二次函数的解析式
转化为顶点式得:
(1)、由 向左平移4个单位得:
(左加右减)
(2)、再将 向下平移3个单位得
(上加下减)
即:所求的解析式为
一、 求二次函数的解析式的一般步骤:
一设、二列、三解、四还原.
二、二次函数常用的几种解析式的确定
1、一般式
已知抛物线上三点的坐标,通常选择一般式。
已知抛物线上顶点坐标(对称轴或最值),通常选择顶点式。
已知抛物线与x轴的交点坐标,选择交点式。
2、顶点式
3、交点式
4、平移式
将抛物线平移,函数解析式中发生变化的只有顶点坐标, 可将原函数先化为顶点式,再根据“左加右减,上加下减”的法则,即可得出所求新函数的解析式。
二次函数关系:
y=ax2 (a≠0)
y=ax2+k (a≠0)
y=a(x-h)2+k (a≠0)
y=ax 2+bx+c (a≠0)
y=a(x-h)2 (a≠0)
顶点式
一般式
y=a(x-x1)(x-x2)(a≠0)
交点式
三、求二次函数解析式的思想方法
1、 求二次函数解析式的常用方法:
2、求二次函数解析式的 常用思想:
3、二次函数解析式的最终形式:
待定系数法、配方法、数形结合等。
转化思想 : 解方程或方程组
无论采用哪一种解析式求解,最后结果最好化为一般式。
活学活用 加深理解
1.某抛物线是将抛物线y=ax2 向右平移一个单位长度,再向上平移一个单位长度得到的,且抛物线过点(3,-3),求该抛物线表达式。
顶点坐标(1,1)设 y=a(x-1)2+1
2.已知二次函数的对称轴是直线x=1,图像上最低点P的纵坐标为-8,图像还过点(-2,10),求此函数的表达式。
顶点坐标(1,-8)设y=a(x-1)2-8
3.已知二次函数的图象与x轴两交点间的距离为4,且当x=1时,函数有最小值-4,求此表达式。
顶点坐标(1,-4)设y=a(x-1)2-4
4.某抛物线与x轴两交点的横坐标为2,6,且函数的最大值为2,求函数的表达式。
顶点坐标(4,2)设y=a(x-4)2+2
2、已知二次函数的图像过原点,当x=1时,y有最小值为
-1,求其解析式。
∴
解:设二次函数的解析式为
∵ x = 1, y= -1 , ∴顶点(1,-1)。
又(0,0)在抛物线上,
∴ a = 1
即:
∴
∴
解:
设 y=a(x+1)2-3
1.已知抛物线的顶点为(-1,-3),与x轴
交点为(0,-5)求抛物线的解析式?
y
o
x
( 0,-5 )
-5=a-3
a=-2
y=-2(x+1)2-3
即:y=-2x2—4x-5
练习
y=-2(x2 + 2x + 1)-3
所以设所求的二次函数为 y=a(x+1)(x-1)
3.已知抛物线与X轴交于A(-1,0),B(1,0)
并经过点M(0,1),求抛物线的解析式?
又∵ 点M( 0,1 )在抛物线上
∴ a(0+1)(0-1)=1
解得: a=-1
故所求的抛物线解析式为 y=- (x+1)(x-1)
即:y=-x2+1
解:因为抛物线与x轴的交点为A(-1,0),B(1,0) ,
选择最优解法,求下列二次函数解析式:
1、已知抛物线的图象经过点(1,4)、(-1,-1)、(2,-2),设抛物线解析式为__________.
2、已知抛物线的顶点坐标(-2,3) ,且经过点(1,4) ,设抛物线解析式为____________.
3、已知二次函数有最大值6,且经过点(2,3),(-4,5),设抛物线解析式为_________.
4、已知抛物线的对称轴是直线x=-2,且经过点(1,3),(5,6),设抛物线解析式为________.
5、已知抛物线与x轴交于点A(-1,0)、B(1,0),且经过点(2,-3),设抛物线解析式为_______.
做一做
题组训练
1、已知二次函数的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6),求二次函数的解析式.
2、已知抛物线的顶点坐标为,与轴交于点,求这条抛物线的解析式。
3、已知抛物线过A(-2,0)、B(1,0)、C(0,2)三点。求这条抛物线的解析式。
4、根据下列条件,求二次函数的解析式。
(1)、图象经过(0,0), (1,-2) , (2,3) 三点;
(2)、图象的顶点(2,3), 且经过点(3,1) ;
(3)、图象经过(-1,0), (3,0) ,(0, 3)。
〔议一议〕
通过上述问题的解决,您能体会到求二次函数表达式采用的一般方法是什么?
(待定系数法)
你能否总结出上述解题的一般步骤?
1.若无坐标系,首先应建立适当的直角坐标系;
2.设抛物线的表达式;
3.写出相关点的坐标;
4.列方程(或方程组);
5.解方程或方程组,求待定系数;
6.写出函数的表达式;
用待定系数法求二次函数的解析式
一、一般式:y=ax?+bx+c (a,b,c为常数,a ≠0)
求二次函数y=ax2+bx+c的解析式,关键是求出待定系数a,b,c的值。
由已知条件(如二次函数图像上三个点的坐标)列出关于a,b,c的方程组,并求出a,b,c,就可以写出二次函数的解析式。
例1 已知:抛物线y=ax2+bx+c过点(2,1)、(1,-2 )(0,5)三点,求抛物线的解析式
解:由题意可得:
{
4a+2b+c=1 ①
a+b+c=-2 ?
c=5 ?
解之得:
{
a=5
b=-12
c=5
所以抛物线的解析式是:y=5x2-12x+5.
练
已知一个二次函数的图象过点(-1,10)、
(1,4)、(2,7)三点,求这个函数的表达式?
o
x
y
解:
设所求的二次函数为 y=ax2+bx+c
由条件得:
a-b+c=10
a+b+c=4
4a+2b+c=7
解方程得:
a=2, b=-3, c=5
所以所求二次函数是:
y=2x2-3x+5
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
二、顶点式y=a(x-h)2+k(a、h、k为常数a≠0).
1.若已知抛物线的顶点坐标和抛物线上的另一个点的坐标时,通过设函数的解析式为顶点式y=a(x-h)2+k.
2. 特别地,当抛物线的顶点为原点是,h=0,k=0,可设函数的解析式为y=ax2.
3.当抛物线的对称轴为y轴时,h=0,可设函数的解析式为y=ax2+k.
4.当抛物线的顶点在x轴上时,k=0,可设函数的解析式为y=a(x-h)2.
解:
1.已知抛物线的顶点为(-1,-3),与y轴交点为(0,-5),求该抛物线的解析式?
y
o
x
所以设所求的二次函数解析式为:y=a(x+1)2-3
因为已知抛物线的顶点为(-1,-3)
又点( 0,-5 )在抛物线上
a-3=-5, 解得a= -2
故所求的抛物线解析式为 y=-2(x+1)2-3
即:y=-2x2-4x-5
2. 已知一个二次函数的图象经过点(4,-3),并且当x=3时有最大值4,试确定这个二次函数的解析式。
解法1:(利用一般式)
设二次函数解析式为:y=ax2+bx+c (a≠0)
由题意知 16a+4b+c = -3
?????? -b/2a = 3
???? (4ac-b2)/4a = 4
解方程组得:?
a= -7
b= 42
c= -59
∴?二次函数的解析式为:y= -7x2+42x-59?
解法2:(利用顶点式)
∵? 当x=3时,有最大值4∴? 顶点坐标为(3,4)
设二次函数解析式为:y=a(x-3)2+4
∵? 函数图象过点(4,- 3)
∴? a(4 - 3)2 +4 = - 3
∴? a= -7
∴?二次函数的解析式为:
y= -7(x-3)2+4
3.二次函数y=ax2+bx+c的图象过点A(0,5), B(5,0)两点,它的对称轴为直线x=3,求这个二次函数的解析式。
解: ∵ 二次函数的对称轴为直线x=3
∴设二次函数表达式为 ? y=a(x-3)2+k
图象过点A(0,5),B(5,0)两点
∴ 5=a(0-3)2+k
0=a(5-3)2+k
解得:a= 1 k=-4
∴?二次函数的表达式: y= (x-3)2-4
即 ? y =x2-6x+5
小结:
已知顶点坐标(h,k)或对称轴方程x=h时优先选用顶点式。
三、交点式y=a(x-x1)(x-x2).(a、x1、x2为常数a≠0)
当抛物线与x轴有两个交点为(x1,0),(x2,0)时,二次函数y=ax2+bx+c可以转化为交点式y=a(x-x1)(x-x2).因此当抛物线与x轴有两个交点为(x1,0),(x2,0)时,可设函数的解析式为y=a(x-x1)(x-x2),在把另一个点的坐标代入其中,即可解得a,求出抛物线的解析式。
交点式y=a(x-x1)(x-x2). x1和x2分别是抛物线与x轴的两个交点的横坐标,这两个交点关于抛物线的对称轴对称,则直线 就是抛物线的对称轴.
1:已知二次函数与x 轴的交点坐标为(-1,0),(1,0),点(0,1)在图像上,求其解析式。
解:设所求的解析式为
∵抛物线与x轴的交点坐标为(-1,0)、(1,0)
∴
又∵点(0,1)在图像上,
∴ a = -1
即:
∴
∴
∴
解:(交点式)
∵二次函数图象经过点 (3,0),(-1,0)
∴设二次函数表达式为 :y=a(x-3)(x+1)
∵ 函数图象过点(1,4)
∴ 4 =a (1-3)(1+1) 得 a= -1
∴ 函数的表达式为:
?y= -(x+1)(x-3)
= -x2+2x+3
2:已知二次函数图象经过点 (1,4),(-1,0)和(3,0)三点,求二次函数的表达式。
知道抛物线与x轴的两个交点的坐标,选用交点式比较简便
其它解法:(一般式)
设二次函数解析式为y=ax2+bx+c
∵二次函数图象过点(1,4),(-1,0)和(3,0)
∴? a+b+c=4?????? ①
??? a-b+c=0?????? ②
?? 9a+3b+c=0??? ? ③
? 解得: a= -1
b=2
c=3
?∴? 函数的解析式为:y= -x2+2x+3
(顶点式)
解:
∵? 抛物线与x轴相交两点(-1,0)和(3,0) ,
∴ (-1+3)/2 = 1
∴? 点(1,4)为抛物线的顶点
可设二次函数解析式为: y=a(x-1)2+4?
∵ 抛物线过点(-1, 0)
∴ 0=a(-1-1)2+4 得 a= -1
∴ 函数的解析式为:
y= -(x-1)2+4
3 已知二次函数的图象在x轴上截得的线段长是4,且当x=1,函数有最小值-4,求这个二次函数的解析式.
(-1, 0)
(3, 0)
X=1
由题意,得:
解:设图象与x轴的交点坐标为
( ,0),( ,0),
把(1,-4)代入上式得:-4=a(1-3)(1+1)
解得:a=1
∴y=x2-2x-3
四、用平移式求二次函数的解析式、
1.将抛物线 向左平移4个单位,再向下平移3个单位,求平移后所得抛物线的解析式。
解法:将二次函数的解析式
转化为顶点式得:
(1)、由 向左平移4个单位得:
(左加右减)
(2)、再将 向下平移3个单位得
(上加下减)
即:所求的解析式为
一、 求二次函数的解析式的一般步骤:
一设、二列、三解、四还原.
二、二次函数常用的几种解析式的确定
1、一般式
已知抛物线上三点的坐标,通常选择一般式。
已知抛物线上顶点坐标(对称轴或最值),通常选择顶点式。
已知抛物线与x轴的交点坐标,选择交点式。
2、顶点式
3、交点式
4、平移式
将抛物线平移,函数解析式中发生变化的只有顶点坐标, 可将原函数先化为顶点式,再根据“左加右减,上加下减”的法则,即可得出所求新函数的解析式。
二次函数关系:
y=ax2 (a≠0)
y=ax2+k (a≠0)
y=a(x-h)2+k (a≠0)
y=ax 2+bx+c (a≠0)
y=a(x-h)2 (a≠0)
顶点式
一般式
y=a(x-x1)(x-x2)(a≠0)
交点式
三、求二次函数解析式的思想方法
1、 求二次函数解析式的常用方法:
2、求二次函数解析式的 常用思想:
3、二次函数解析式的最终形式:
待定系数法、配方法、数形结合等。
转化思想 : 解方程或方程组
无论采用哪一种解析式求解,最后结果最好化为一般式。
活学活用 加深理解
1.某抛物线是将抛物线y=ax2 向右平移一个单位长度,再向上平移一个单位长度得到的,且抛物线过点(3,-3),求该抛物线表达式。
顶点坐标(1,1)设 y=a(x-1)2+1
2.已知二次函数的对称轴是直线x=1,图像上最低点P的纵坐标为-8,图像还过点(-2,10),求此函数的表达式。
顶点坐标(1,-8)设y=a(x-1)2-8
3.已知二次函数的图象与x轴两交点间的距离为4,且当x=1时,函数有最小值-4,求此表达式。
顶点坐标(1,-4)设y=a(x-1)2-4
4.某抛物线与x轴两交点的横坐标为2,6,且函数的最大值为2,求函数的表达式。
顶点坐标(4,2)设y=a(x-4)2+2
2、已知二次函数的图像过原点,当x=1时,y有最小值为
-1,求其解析式。
∴
解:设二次函数的解析式为
∵ x = 1, y= -1 , ∴顶点(1,-1)。
又(0,0)在抛物线上,
∴ a = 1
即:
∴
∴
解:
设 y=a(x+1)2-3
1.已知抛物线的顶点为(-1,-3),与x轴
交点为(0,-5)求抛物线的解析式?
y
o
x
( 0,-5 )
-5=a-3
a=-2
y=-2(x+1)2-3
即:y=-2x2—4x-5
练习
y=-2(x2 + 2x + 1)-3
所以设所求的二次函数为 y=a(x+1)(x-1)
3.已知抛物线与X轴交于A(-1,0),B(1,0)
并经过点M(0,1),求抛物线的解析式?
又∵ 点M( 0,1 )在抛物线上
∴ a(0+1)(0-1)=1
解得: a=-1
故所求的抛物线解析式为 y=- (x+1)(x-1)
即:y=-x2+1
解:因为抛物线与x轴的交点为A(-1,0),B(1,0) ,
选择最优解法,求下列二次函数解析式:
1、已知抛物线的图象经过点(1,4)、(-1,-1)、(2,-2),设抛物线解析式为__________.
2、已知抛物线的顶点坐标(-2,3) ,且经过点(1,4) ,设抛物线解析式为____________.
3、已知二次函数有最大值6,且经过点(2,3),(-4,5),设抛物线解析式为_________.
4、已知抛物线的对称轴是直线x=-2,且经过点(1,3),(5,6),设抛物线解析式为________.
5、已知抛物线与x轴交于点A(-1,0)、B(1,0),且经过点(2,-3),设抛物线解析式为_______.
做一做
题组训练
1、已知二次函数的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6),求二次函数的解析式.
2、已知抛物线的顶点坐标为,与轴交于点,求这条抛物线的解析式。
3、已知抛物线过A(-2,0)、B(1,0)、C(0,2)三点。求这条抛物线的解析式。
4、根据下列条件,求二次函数的解析式。
(1)、图象经过(0,0), (1,-2) , (2,3) 三点;
(2)、图象的顶点(2,3), 且经过点(3,1) ;
(3)、图象经过(-1,0), (3,0) ,(0, 3)。
〔议一议〕
通过上述问题的解决,您能体会到求二次函数表达式采用的一般方法是什么?
(待定系数法)
你能否总结出上述解题的一般步骤?
1.若无坐标系,首先应建立适当的直角坐标系;
2.设抛物线的表达式;
3.写出相关点的坐标;
4.列方程(或方程组);
5.解方程或方程组,求待定系数;
6.写出函数的表达式;
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
