人教 版数学九年级下册27.3位似图形课件(共22张ppt)
文档属性
| 名称 | 人教 版数学九年级下册27.3位似图形课件(共22张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:59:17 | ||
图片预览




文档简介
位似图形
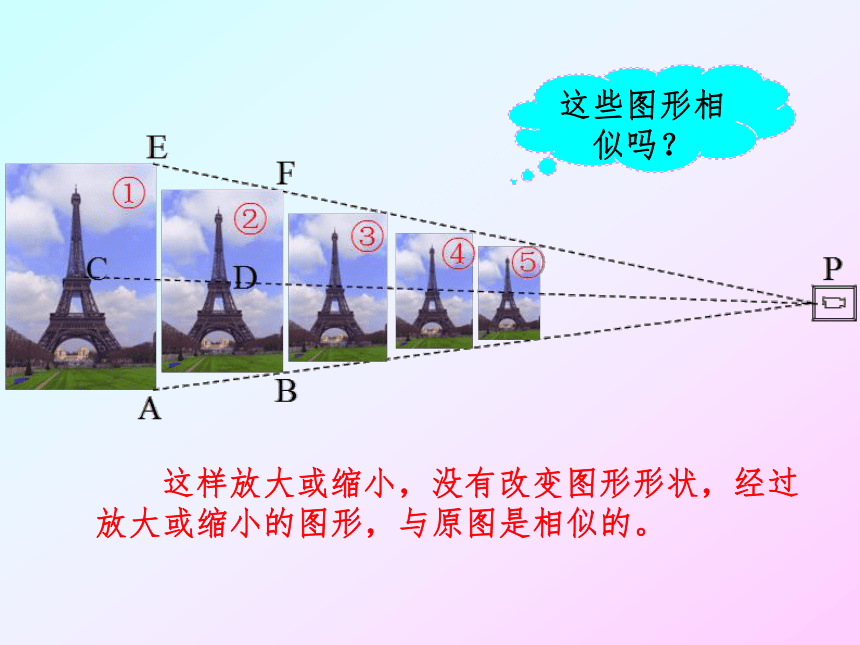
这样放大或缩小,没有改变图形形状,经过放大或缩小的图形,与原图是相似的。
这些图形相似吗?
在幻灯机放映图片的过程中,这些图片有
什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
合作探究 达成目标
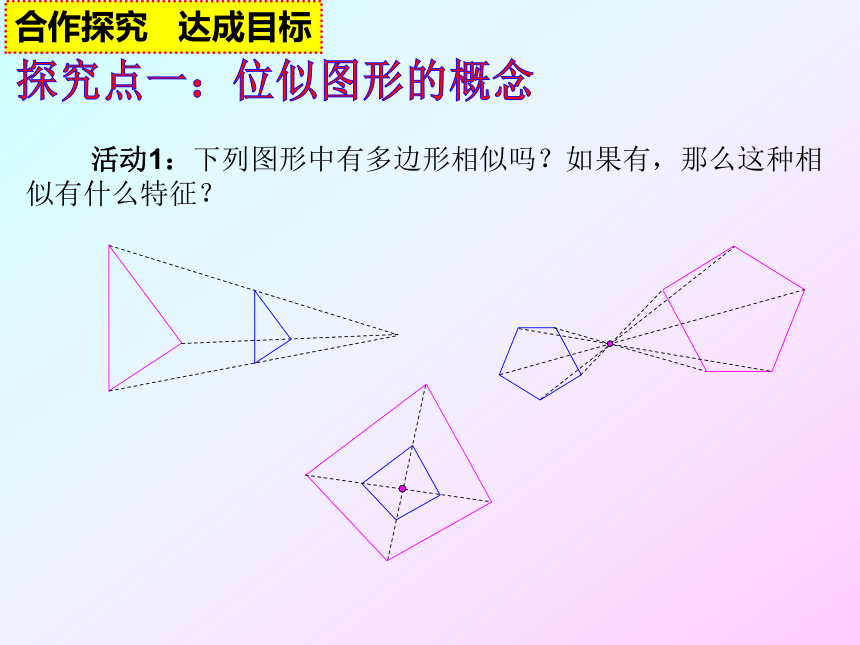
活动1:下列图形中有多边形相似吗?如果有,那么这种相似有什么特征?
观察与思考
?
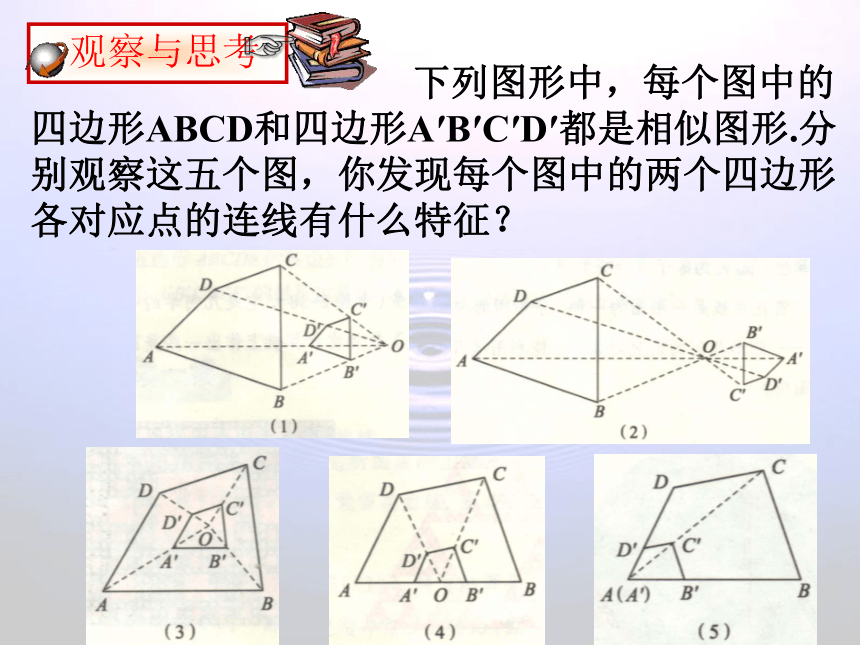
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?
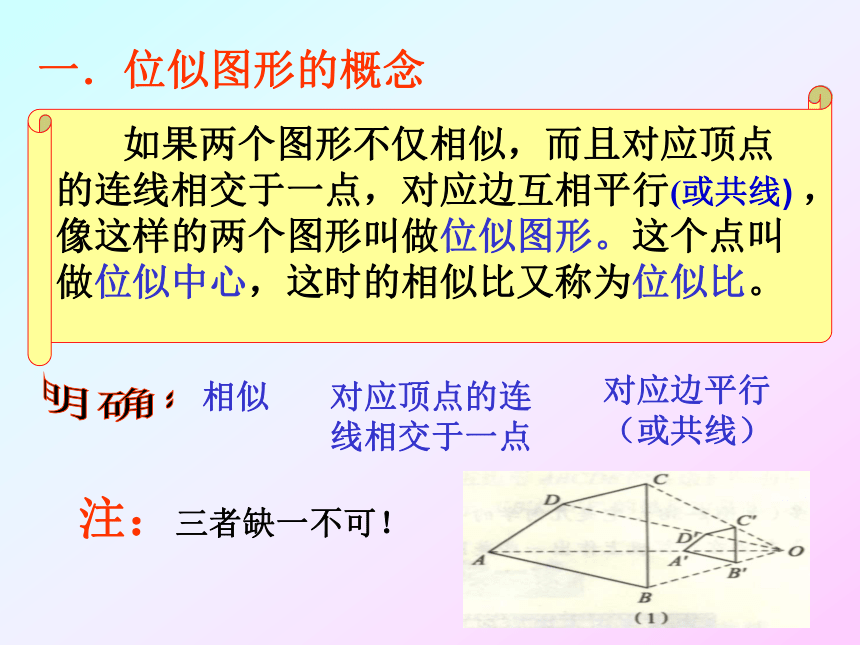
一.位似图形的概念
相似
对应顶点的连线相交于一点
对应边平行(或共线)
注:三者缺一不可!
如果两个图形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行(或共线) ,像这样的两个图形叫做位似图形。这个点叫做位似中心,这时的相似比又称为位似比。
位似图形
小练习
D
E
F
A
O
B
C
思考:判定位似图形或确定位似中心的方法?
每组对应点所在的直线是否经过同一点
例2、判断下列各对图形哪些是相似图形,哪些是位似图形.
结论1:位似图形是相似 图形的特殊情形,位似的要求更为苛刻。
相似且位似
相似但不是位似
A
B
C
D
E
F
G
相似但不是位似
②∠AED=∠B
①DE∥BC
③两个正方形
观察下列位似图形的位似中心,你发现了什么?
结论2:位似中心的位置由两个图形的位置决定,可能在
两个图形的同侧,异侧,图形的内部,边上,或顶点上
2. 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
二. 位似图形的性质
⑵特殊性质:位似图形上任意一对对应顶点到位似中心的距离之比等于位似比.
⑴一般性质:具有相似多边形的性质
周长比等于位似比
面积比等于位似比的平方
位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。
注意
对应点与位似中心共线。
不经过位似中心的对应边平行。
位似图形上任意一对应点到位似中心的距离之比等于位似比。
位似图形的性质
不经过位似中心的对应线段平行.
在下列每个图形中,位似图形的对应线段AB与A′B′是否平行?BC与B′C′,CD与C′D′,AD与A′D′是否平行?为什么?
如图,已知△ABC∽△DEF, 它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形?
0
B
E
C
F
A
D
位似的作用
位似可以将一个图形放大或缩小。
O
.
A
B
C
A'
C’
B’
.
1.如图,已知△ABC和点O.以O为位似中心,求作△A’B’C’ 和△ABC位似,且位似比为2.
OA’:OA =OB’:OB =OC’:OC= 2:1
特殊性质在作图中的运用
.
.
注:在作图中,如无特殊说明,位似比通常代表新图形与原图形的比。
k﹥1,将原图形放大,0<k<1,将原图形缩小
确定位似中心
画出图形
确定位似比
确定原图的关键点
找出新图形的对应关键点
①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。
位似变换的步骤
达标检测 反思目标
3.如图,△ABC与△DEF是位似图形,位似比
为2∶3,已知AB=4,则DE的长为_____.
6
这样放大或缩小,没有改变图形形状,经过放大或缩小的图形,与原图是相似的。
这些图形相似吗?
在幻灯机放映图片的过程中,这些图片有
什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
合作探究 达成目标
活动1:下列图形中有多边形相似吗?如果有,那么这种相似有什么特征?
观察与思考
?
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?
一.位似图形的概念
相似
对应顶点的连线相交于一点
对应边平行(或共线)
注:三者缺一不可!
如果两个图形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行(或共线) ,像这样的两个图形叫做位似图形。这个点叫做位似中心,这时的相似比又称为位似比。
位似图形
小练习
D
E
F
A
O
B
C
思考:判定位似图形或确定位似中心的方法?
每组对应点所在的直线是否经过同一点
例2、判断下列各对图形哪些是相似图形,哪些是位似图形.
结论1:位似图形是相似 图形的特殊情形,位似的要求更为苛刻。
相似且位似
相似但不是位似
A
B
C
D
E
F
G
相似但不是位似
②∠AED=∠B
①DE∥BC
③两个正方形
观察下列位似图形的位似中心,你发现了什么?
结论2:位似中心的位置由两个图形的位置决定,可能在
两个图形的同侧,异侧,图形的内部,边上,或顶点上
2. 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
二. 位似图形的性质
⑵特殊性质:位似图形上任意一对对应顶点到位似中心的距离之比等于位似比.
⑴一般性质:具有相似多边形的性质
周长比等于位似比
面积比等于位似比的平方
位似是一种具有位置关系的相似。
位似图形是相似图形的特殊情形。
位似图形必定是相似图形,而相似图形不一定是位似图形。
两个位似图形的位似中心只有一个。
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧。
注意
对应点与位似中心共线。
不经过位似中心的对应边平行。
位似图形上任意一对应点到位似中心的距离之比等于位似比。
位似图形的性质
不经过位似中心的对应线段平行.
在下列每个图形中,位似图形的对应线段AB与A′B′是否平行?BC与B′C′,CD与C′D′,AD与A′D′是否平行?为什么?
如图,已知△ABC∽△DEF, 它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形?
0
B
E
C
F
A
D
位似的作用
位似可以将一个图形放大或缩小。
O
.
A
B
C
A'
C’
B’
.
1.如图,已知△ABC和点O.以O为位似中心,求作△A’B’C’ 和△ABC位似,且位似比为2.
OA’:OA =OB’:OB =OC’:OC= 2:1
特殊性质在作图中的运用
.
.
注:在作图中,如无特殊说明,位似比通常代表新图形与原图形的比。
k﹥1,将原图形放大,0<k<1,将原图形缩小
确定位似中心
画出图形
确定位似比
确定原图的关键点
找出新图形的对应关键点
①确定位似中心,位似中心的位置可随意选择;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形。
位似变换的步骤
达标检测 反思目标
3.如图,△ABC与△DEF是位似图形,位似比
为2∶3,已知AB=4,则DE的长为_____.
6
