15.2.3 整数指数幂 课件
图片预览






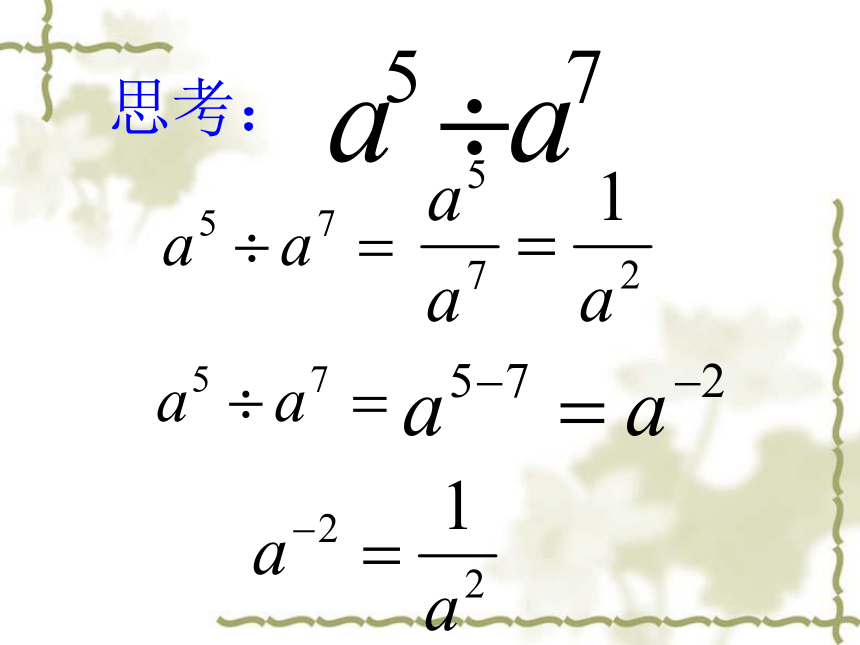





文档简介
人教版八年级数学上册 15.2 分式的运算
15.2.3 整数指数幂
理解负整数指数幂的意义;
掌握整数指数幂的运算性质;
会用科学记数法表示小于1的数。
学习目标
复习旧知,引入新课
算一算,并分别说出每一小题所用的运算性质.
(1) = ;
(2) = ;
同底数幂的乘法:
(m,n是正整数)
幂的乘方:
(m,n是正整数)
(3) = ;
积的乘方:
(n是正整数)
复习旧知,引入新课
算一算,并分别说出每一小题所用的运算性质.
(4) = ;
同底数幂的除法:
(a≠0,m,n是正整数且
m>n )
(5) = ;
商的乘方:
(b≠0,n是正整数)
正整数指数幂的运算性质:
1.同底数的幂的乘法: (m,n是正整数);
2.幂的乘方: (m,n是正整数);
3.积的乘方: (n是正整数);
4.同底数的幂的除法: ( a≠0,m,n是正整数m>n);
5.商的乘方: (n是正整数);
6.0指数幂,即当a≠0时, .
思考:
一般地,a m中指数m可以是负整数吗?如果可以,那么负整数指数幂a m表示什么?
思考:
思考:
其中a≠0,n是正整数
负指数的意义:
一般地,当n是正整数时,
这就是说:a-n(a≠0)是an 的倒数
例1 填空:
(1) 2-1=___, 3-1=___, x-1=___.
(2) (-2) -1=___, (-3) -1=___, (-x) -1=___.
(3) 4-2=___, (-4) -2=___, -4-2= .
2、填空:
(1) = ;
(2) = ;
(3) = ;
(4) = .
(5) = = ;
(6) = ;
例2、把下列各式转化为只含有正整数指数幂的形式
1、a-3
2、x3y-2
3、2(m+n)-2
4、
5、
6、
正整数指数幂的运算性质是否适合负指数呢?
(1)am·an=am+n (a≠0)
(2)(am)n=amn (a≠0)
(3)(ab)n=anbn (a,b≠0)
(4)am÷an=am-n (a≠0)
(5) (b≠0)
整数指数幂有以下运算性质:
当a≠0时,a0=1。
(6)
a-3·a-9=
(a-3)2=
(ab)-3=
a-3÷a-5=
巩固练习,精练提高
例1 计算:
.
(1) ;
(2) ;
(3) ;
(4) .
解:
(1)
(2)
(3)
(4)
计算:
解:
巩固练习,精炼提高
练习:
巩固练习,精炼提高
练习:
(1)
(2)
(3)
计算
光速:300 000 000=3×108米/秒;
太阳半径:696 000=6.96×105千米;
目前我国人口:6 100 000 000=6.1×109.
在七年级我们学过,一些较大的数字可以用科学记数法来表示:
类似地,我们可以利用10的负整数次幂,
用科学记数法表示一些绝对值较小的数,
即将它们表示成a×10- n的形式,其中n是
正整数,1≤∣a∣<10.
类似:
算一算:
10-2= -------------- 10-4= -------------
10-8= ----------------------
议一议:
指数与运算结果的0的个数有什么关系?
一般地,10的-n次幂,在1前面有--------个0。
仔细想一想:
10-21的小数点后的位数是几位? 1前面有几个零?
0.01
0.0001
0.00000001
n
与运算结果的小数点后的位数有什么关系?
你发现了什么?
探索:
学了就用
?
6.75×10-7
9.9×10-10
用科学记数法表示:
(1) 0.000000675=
(2) 0.00000000099=
(3)-0.0000000061=
- 6.1×10-9
分析:把a×10-n还原成原数时,只需把a的小数点
向左移动n位。
(1)7.2×10-5=
(2)1.5×10-4=
用小数表示下列各数
用科学计数法表示下列各数:
0.00001,-0.025,0.00000032,
0.000406
小练习
随堂练习
用小数表示下列各数:
0.000 000 004,
0.0035,
-0.000 000 254 ,
-0.000 04,
0.000 000 040 35,
5 870 000.
2.计算:
(1)(5×10-4) ×(1.8×105);
(2) (4×10-7)3÷(10-5)2.
3.用科学计数法把0.000 005 042表示成
5.042×10n,那么n=___.
-6
90
小练习
小
结
(1)n是正整数时, a-n属于分式,并且
(a≠0)
(2)科学计数法表示小于1的小数:
a×10-n
(a 是整数位只有一位的正数,n是正整数。)
15.2.3 整数指数幂
理解负整数指数幂的意义;
掌握整数指数幂的运算性质;
会用科学记数法表示小于1的数。
学习目标
复习旧知,引入新课
算一算,并分别说出每一小题所用的运算性质.
(1) = ;
(2) = ;
同底数幂的乘法:
(m,n是正整数)
幂的乘方:
(m,n是正整数)
(3) = ;
积的乘方:
(n是正整数)
复习旧知,引入新课
算一算,并分别说出每一小题所用的运算性质.
(4) = ;
同底数幂的除法:
(a≠0,m,n是正整数且
m>n )
(5) = ;
商的乘方:
(b≠0,n是正整数)
正整数指数幂的运算性质:
1.同底数的幂的乘法: (m,n是正整数);
2.幂的乘方: (m,n是正整数);
3.积的乘方: (n是正整数);
4.同底数的幂的除法: ( a≠0,m,n是正整数m>n);
5.商的乘方: (n是正整数);
6.0指数幂,即当a≠0时, .
思考:
一般地,a m中指数m可以是负整数吗?如果可以,那么负整数指数幂a m表示什么?
思考:
思考:
其中a≠0,n是正整数
负指数的意义:
一般地,当n是正整数时,
这就是说:a-n(a≠0)是an 的倒数
例1 填空:
(1) 2-1=___, 3-1=___, x-1=___.
(2) (-2) -1=___, (-3) -1=___, (-x) -1=___.
(3) 4-2=___, (-4) -2=___, -4-2= .
2、填空:
(1) = ;
(2) = ;
(3) = ;
(4) = .
(5) = = ;
(6) = ;
例2、把下列各式转化为只含有正整数指数幂的形式
1、a-3
2、x3y-2
3、2(m+n)-2
4、
5、
6、
正整数指数幂的运算性质是否适合负指数呢?
(1)am·an=am+n (a≠0)
(2)(am)n=amn (a≠0)
(3)(ab)n=anbn (a,b≠0)
(4)am÷an=am-n (a≠0)
(5) (b≠0)
整数指数幂有以下运算性质:
当a≠0时,a0=1。
(6)
a-3·a-9=
(a-3)2=
(ab)-3=
a-3÷a-5=
巩固练习,精练提高
例1 计算:
.
(1) ;
(2) ;
(3) ;
(4) .
解:
(1)
(2)
(3)
(4)
计算:
解:
巩固练习,精炼提高
练习:
巩固练习,精炼提高
练习:
(1)
(2)
(3)
计算
光速:300 000 000=3×108米/秒;
太阳半径:696 000=6.96×105千米;
目前我国人口:6 100 000 000=6.1×109.
在七年级我们学过,一些较大的数字可以用科学记数法来表示:
类似地,我们可以利用10的负整数次幂,
用科学记数法表示一些绝对值较小的数,
即将它们表示成a×10- n的形式,其中n是
正整数,1≤∣a∣<10.
类似:
算一算:
10-2= -------------- 10-4= -------------
10-8= ----------------------
议一议:
指数与运算结果的0的个数有什么关系?
一般地,10的-n次幂,在1前面有--------个0。
仔细想一想:
10-21的小数点后的位数是几位? 1前面有几个零?
0.01
0.0001
0.00000001
n
与运算结果的小数点后的位数有什么关系?
你发现了什么?
探索:
学了就用
?
6.75×10-7
9.9×10-10
用科学记数法表示:
(1) 0.000000675=
(2) 0.00000000099=
(3)-0.0000000061=
- 6.1×10-9
分析:把a×10-n还原成原数时,只需把a的小数点
向左移动n位。
(1)7.2×10-5=
(2)1.5×10-4=
用小数表示下列各数
用科学计数法表示下列各数:
0.00001,-0.025,0.00000032,
0.000406
小练习
随堂练习
用小数表示下列各数:
0.000 000 004,
0.0035,
-0.000 000 254 ,
-0.000 04,
0.000 000 040 35,
5 870 000.
2.计算:
(1)(5×10-4) ×(1.8×105);
(2) (4×10-7)3÷(10-5)2.
3.用科学计数法把0.000 005 042表示成
5.042×10n,那么n=___.
-6
90
小练习
小
结
(1)n是正整数时, a-n属于分式,并且
(a≠0)
(2)科学计数法表示小于1的小数:
a×10-n
(a 是整数位只有一位的正数,n是正整数。)
