人教版七年级上册数学课件:3.2解一元一次方程移项(共21张ppt)
文档属性
| 名称 | 人教版七年级上册数学课件:3.2解一元一次方程移项(共21张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:38:20 | ||
图片预览





文档简介
解一元一次方程
——移项
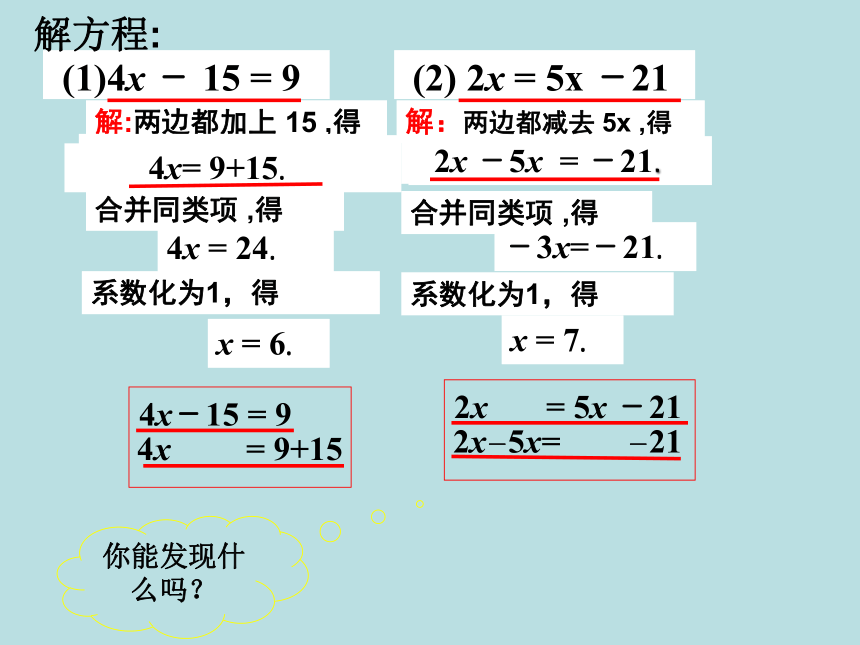
(1)4x - 15 = 9
解:两边都减去 5x ,得
-3x=-21.
系数化为1,得
x = 6.
(2) 2x = 5x -21
解:两边都加上 15 ,得
系数化为1,得
x = 7.
合并同类项 ,得
合并同类项 ,得
4x = 24.
2x = 5x –21
4x – 15 = 9
+ 15
+ 15
–5x
–5x
4x-15 = 9
4x = 9+15
2x = 5x -21
2x-5x= -21
4x= 9+15.
2x -5x = -21.
你能发现什么吗?
解方程:
4x –15 = 9
①
4x = 9 +15
②
这个变形相当于把 ①中的 “– 15”这一项
由方程 ①
到方程 ② ,
“– 15”这项移动后,发生了什么变化?
改变了符号
从方程的左边移到
了方程的右边.
讲授新课
2
-15
4x-15 = 9
4x = 9+15
2x = 5x – 21
③
2x –5x = – 21
④
这个变形相当于把 ③ 中的 “5x”这一项
由方程 ③
到方程 ④ ,
“5x”这项移动后发生了什么变化?
改变了符号.
从方程的右边移到了方程的左边.
5x
2x = 5x -21
2x-5x= -21
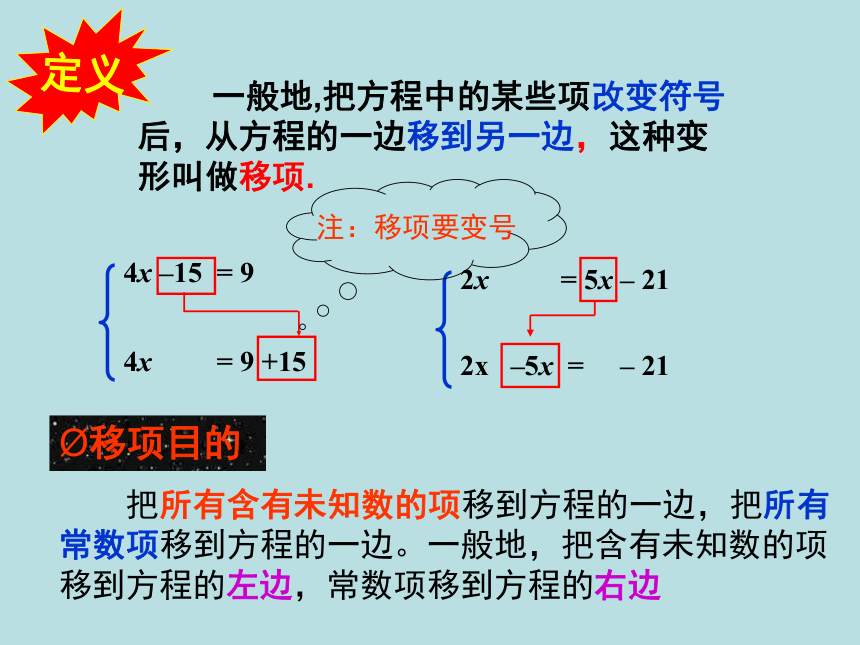
一般地,把方程中的某些项改变符号
后,从方程的一边移到另一边,这种变
形叫做移项.
定义
2x = 5x – 21
2x –5x = – 21
4x –15 = 9
4x = 9 +15
移项目的
把所有含有未知数的项移到方程的一边,把所有常数项移到方程的一边。一般地,把含有未知数的项移到方程的左边,常数项移到方程的右边
注:移项要变号
移项
移项
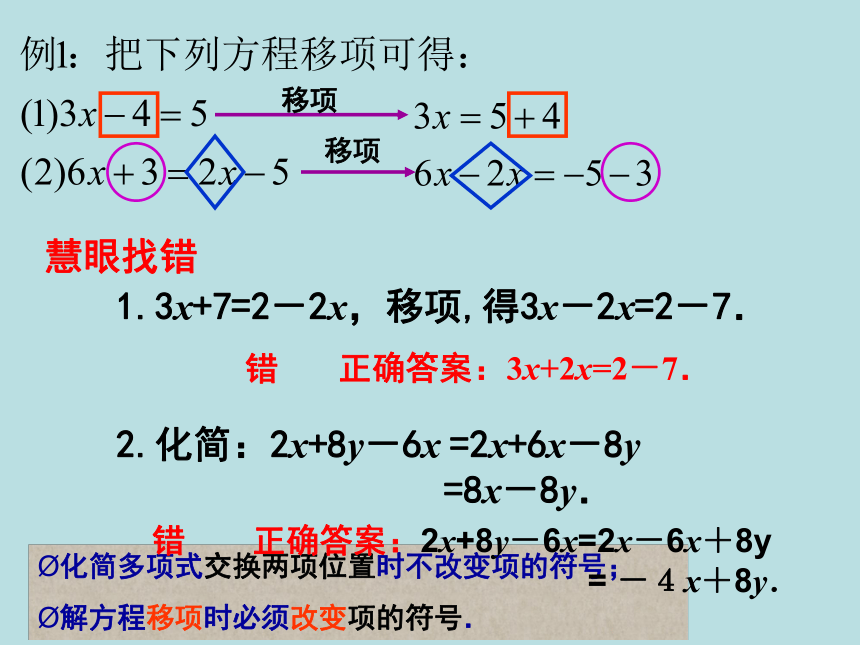
慧眼找错
3x+7=2-2x,移项,得3x-2x=2-7.
2.化简:2x+8y-6x =2x+6x-8y
=8x-8y.
化简多项式交换两项位置时不改变项的符号;
解方程移项时必须改变项的符号.
错
正确答案:3x+2x=2-7.
正确答案:2x+8y-6x=2x-6x+8y
= -4x+8y.
错
问题2:把一些图书分给某班同学阅读,如果每人3
本,则剩余20本,若每人4本,则还缺少25
本,这个班有多少学生?
分析:设这个班有 x 人。
1、每人分3本,那么共分出多少本?
2、共分出的 本和剩余的20本,可知道什么?
答:这批书共有本 .
3、每人分4本,那么需要分出多少本?
4、需要分出的 本和还缺少25本,那么这批
书共有多少本?
答:这批书共有 本。
3 +20 = 4 -25
3x
(3x +20)
4x
(4 x -25)
表示同一个量的两个不同
的式子相等。
书的总数=书的总数
移项
合并
系数化为1
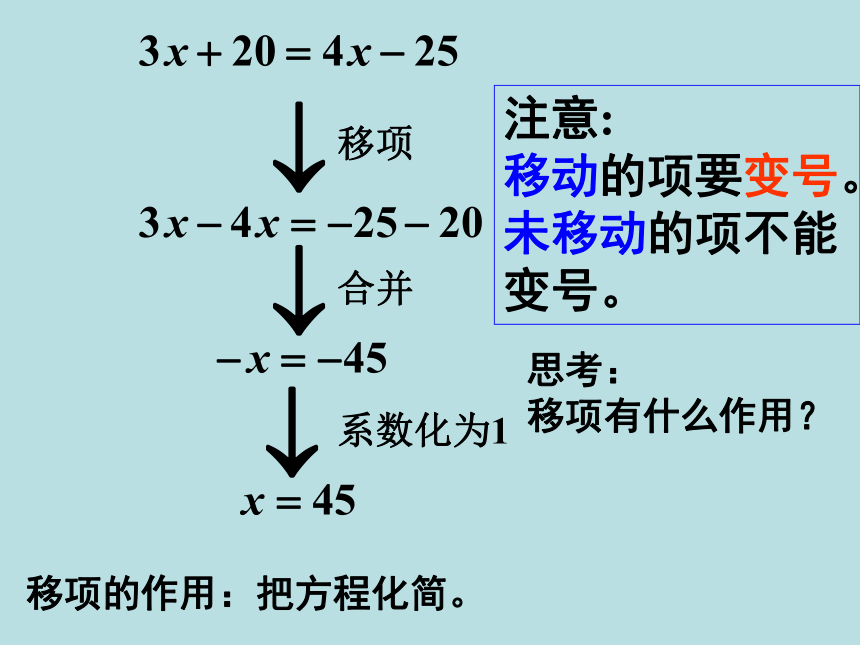
思考:
移项有什么作用?
注意:
移动的项要变号。
未移动的项不能变号。
移项的作用:把方程化简。
有一个班的同学去划船,他们算了一下,在原有船的情况下如果增加一条船,正好每条船坐6人,如果减少一条船,正好每条船坐9人,问:这个班共有多少同学?
综合应用
解法一:设船有x条,则
解法二:设这个班共有同学x人。
得出x=36
答:这个班共有36人。
同学人数=同学人数
原有船的数量=原有船的数量
6(x+1)=9(x-1)
得出x=5
6×(5+1)=36(人)
例2 解方程
观察与思考:
移项时需要移哪些项?为什么?
解:移项,得
合并同类项 ,得
例2 解方程
解一元一次方程时,
一般把含未知数的项移
到方程的左边,常数项
移到方程的右边.
系数化为1,得
例题3:
解:
移项,得:
合并同类项,得:
化系数为1,得:
练习6 解下列一元一次方程
1. :一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
3.移项要改变符号.
2.解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).
这节课我们学习了什么?
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出 本,加上剩余
的20本,这批书共 本.
每人分4本,需要 本,减去缺少
的25本,这批书共 本.
设这个班有x名学生.
这批书的总数有几种
表示法?
它们之间有什么关系?
表示这批书的总数的两个代数式相等.
实际问题
解:设这个班有x名学生,根据题意得
反思例题:
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
表示这批书的总数的两个代数式相等.
“表示同一个量的两个不同的式子相等”
是一个基本的相等关系。
巩固训练:
教材91页11题,90页2题
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
思考:
(1)你准备设哪个未知数?
(2)你能在问题中把表示等量关系的语句
找出来,并用等式进行表示吗?
等号两边代表哪个数量?
解:设新、旧工艺的废水排量分别为2x t和5x t.
根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100
移项,得
5x-2x=100+200
合并同类项,得
3x=300
所以 2x=200,
5x=500.
系数化为1,得
x=100
答:新旧工艺产生的废水数量分别为200 t和500 t.
“表示同一个量的两个不同的式子相等”
是一个基本的相等关系。
环保限制最大量
一个三角形三边长度的比为3:4:5,最短的边
比最长的边短4 cm,则这个三角形的周长是多少?
解:由已知可设三角形三边的长度分别为3x,4x,
5x,根据题意,得
解得 x=2
所以 3x=3×2=6
4x=4×2=8
5x=5×2=10
答:这个三角形的周长是24.
周长=6+8+10=24.
巩固训练
1. :一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
2.移项要改变符号.
解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).
这节课我们学习了什么?
3.“表示同一个量的两个不同的式子相等”
是一个基本的相等关系。
谢谢你们认真听课!
这是对老师最大的鼓励!
——移项
(1)4x - 15 = 9
解:两边都减去 5x ,得
-3x=-21.
系数化为1,得
x = 6.
(2) 2x = 5x -21
解:两边都加上 15 ,得
系数化为1,得
x = 7.
合并同类项 ,得
合并同类项 ,得
4x = 24.
2x = 5x –21
4x – 15 = 9
+ 15
+ 15
–5x
–5x
4x-15 = 9
4x = 9+15
2x = 5x -21
2x-5x= -21
4x= 9+15.
2x -5x = -21.
你能发现什么吗?
解方程:
4x –15 = 9
①
4x = 9 +15
②
这个变形相当于把 ①中的 “– 15”这一项
由方程 ①
到方程 ② ,
“– 15”这项移动后,发生了什么变化?
改变了符号
从方程的左边移到
了方程的右边.
讲授新课
2
-15
4x-15 = 9
4x = 9+15
2x = 5x – 21
③
2x –5x = – 21
④
这个变形相当于把 ③ 中的 “5x”这一项
由方程 ③
到方程 ④ ,
“5x”这项移动后发生了什么变化?
改变了符号.
从方程的右边移到了方程的左边.
5x
2x = 5x -21
2x-5x= -21
一般地,把方程中的某些项改变符号
后,从方程的一边移到另一边,这种变
形叫做移项.
定义
2x = 5x – 21
2x –5x = – 21
4x –15 = 9
4x = 9 +15
移项目的
把所有含有未知数的项移到方程的一边,把所有常数项移到方程的一边。一般地,把含有未知数的项移到方程的左边,常数项移到方程的右边
注:移项要变号
移项
移项
慧眼找错
3x+7=2-2x,移项,得3x-2x=2-7.
2.化简:2x+8y-6x =2x+6x-8y
=8x-8y.
化简多项式交换两项位置时不改变项的符号;
解方程移项时必须改变项的符号.
错
正确答案:3x+2x=2-7.
正确答案:2x+8y-6x=2x-6x+8y
= -4x+8y.
错
问题2:把一些图书分给某班同学阅读,如果每人3
本,则剩余20本,若每人4本,则还缺少25
本,这个班有多少学生?
分析:设这个班有 x 人。
1、每人分3本,那么共分出多少本?
2、共分出的 本和剩余的20本,可知道什么?
答:这批书共有本 .
3、每人分4本,那么需要分出多少本?
4、需要分出的 本和还缺少25本,那么这批
书共有多少本?
答:这批书共有 本。
3 +20 = 4 -25
3x
(3x +20)
4x
(4 x -25)
表示同一个量的两个不同
的式子相等。
书的总数=书的总数
移项
合并
系数化为1
思考:
移项有什么作用?
注意:
移动的项要变号。
未移动的项不能变号。
移项的作用:把方程化简。
有一个班的同学去划船,他们算了一下,在原有船的情况下如果增加一条船,正好每条船坐6人,如果减少一条船,正好每条船坐9人,问:这个班共有多少同学?
综合应用
解法一:设船有x条,则
解法二:设这个班共有同学x人。
得出x=36
答:这个班共有36人。
同学人数=同学人数
原有船的数量=原有船的数量
6(x+1)=9(x-1)
得出x=5
6×(5+1)=36(人)
例2 解方程
观察与思考:
移项时需要移哪些项?为什么?
解:移项,得
合并同类项 ,得
例2 解方程
解一元一次方程时,
一般把含未知数的项移
到方程的左边,常数项
移到方程的右边.
系数化为1,得
例题3:
解:
移项,得:
合并同类项,得:
化系数为1,得:
练习6 解下列一元一次方程
1. :一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
3.移项要改变符号.
2.解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).
这节课我们学习了什么?
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出 本,加上剩余
的20本,这批书共 本.
每人分4本,需要 本,减去缺少
的25本,这批书共 本.
设这个班有x名学生.
这批书的总数有几种
表示法?
它们之间有什么关系?
表示这批书的总数的两个代数式相等.
实际问题
解:设这个班有x名学生,根据题意得
反思例题:
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
表示这批书的总数的两个代数式相等.
“表示同一个量的两个不同的式子相等”
是一个基本的相等关系。
巩固训练:
教材91页11题,90页2题
某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
思考:
(1)你准备设哪个未知数?
(2)你能在问题中把表示等量关系的语句
找出来,并用等式进行表示吗?
等号两边代表哪个数量?
解:设新、旧工艺的废水排量分别为2x t和5x t.
根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100
移项,得
5x-2x=100+200
合并同类项,得
3x=300
所以 2x=200,
5x=500.
系数化为1,得
x=100
答:新旧工艺产生的废水数量分别为200 t和500 t.
“表示同一个量的两个不同的式子相等”
是一个基本的相等关系。
环保限制最大量
一个三角形三边长度的比为3:4:5,最短的边
比最长的边短4 cm,则这个三角形的周长是多少?
解:由已知可设三角形三边的长度分别为3x,4x,
5x,根据题意,得
解得 x=2
所以 3x=3×2=6
4x=4×2=8
5x=5×2=10
答:这个三角形的周长是24.
周长=6+8+10=24.
巩固训练
1. :一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
2.移项要改变符号.
解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).
这节课我们学习了什么?
3.“表示同一个量的两个不同的式子相等”
是一个基本的相等关系。
谢谢你们认真听课!
这是对老师最大的鼓励!
