人教版数学九年级上册 《24.1.1 圆》课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级上册 《24.1.1 圆》课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 822.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 22:03:15 | ||
图片预览





文档简介
第二十四章 圆的有关性质
人教版数学九年级上册
24.1.1 圆
学习目标
1.巩固圆及其相关结论概念,深入理解圆的轴对称性和中心对称性.
2.掌握垂径定理,圆心角、弧、弦之间关系定理以及圆周角和圆心角关系定理.
3.进一步认识和理解圆的有关性质.
导入新知
圆是生活中常见的图形,许多物体都给我们以圆的形象.
1.观察以上图形,体验圆的和谐与美丽.请大家说说生活中还有哪些圆形?
2.请同学们在草稿纸上用圆规画圆,体验画圆的过程,想想圆是怎样形成的.
导入新知
我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?
合作探究
新知一
·
r
O
A
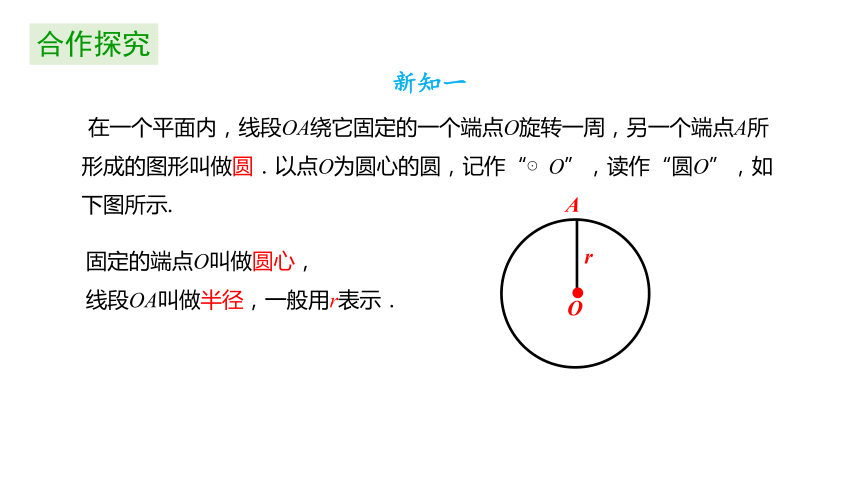
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”,如下图所示.
固定的端点O叫做圆心,
线段OA叫做半径,一般用r表示.
合作探究
新知一
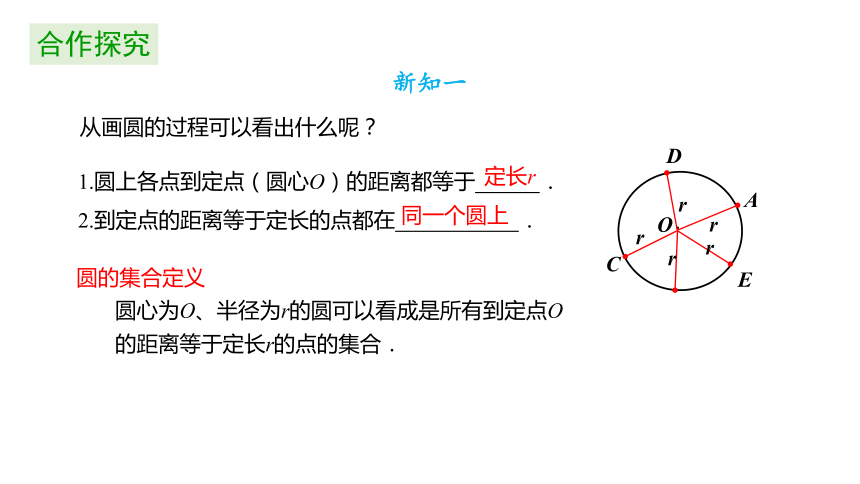
1.圆上各点到定点(圆心O)的距离都等于 .
2.到定点的距离等于定长的点都在 .
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
O
·
A
C
E
r
r
r
r
r
D
定长r
同一个圆上
圆的集合定义
从画圆的过程可以看出什么呢?
合作探究
新知一
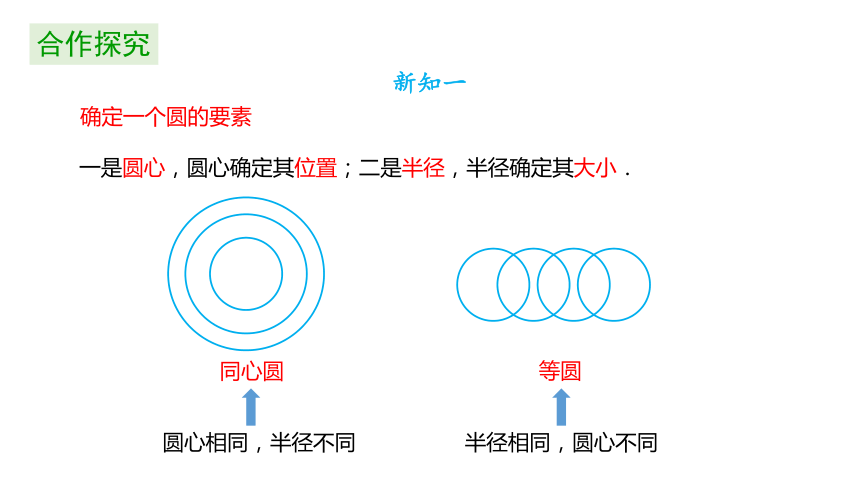
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
合作探究
新知一
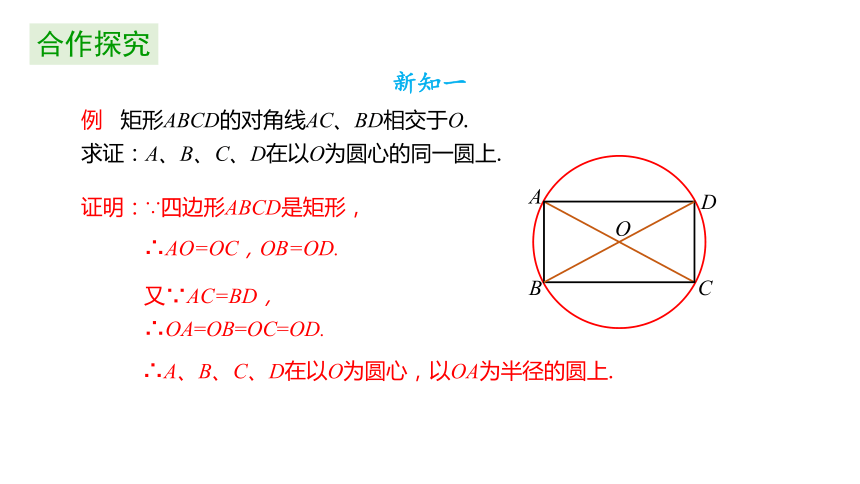
例 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
合作探究
新知一
下列条件中,可以确定一个圆的是( )
D
A.半径为1 cm B.圆心在点O处
C.半径是1 cm,且经过点P D.圆心在点O处,且直径是2 cm
典型例题
·
C
O
A
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
注意
合作探究
新知二
O
A
B
O
A
B
圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
直径是最长的弦
合作探究
新知二
·
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
C
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧,如图中的AC ;
(
大于半圆的弧叫做优弧,如图中的ABC.
(
合作探究
新知二
·
C
O
A
能够重合的两个圆叫做等圆.
·
C
O1
A
在同圆或等圆中,能够互相重合的弧叫做等弧.
等弧仅仅存在于同圆或者等圆中.
合作探究
新知二
注意
下列语句正确的有( )
①直径是弦;
②弦是直径;
③半径相等的两个半圆是等弧;
④长度相等的两条弧是等弧;
⑤半圆是弧,弧不一定是半圆.
A.1个 B.2个 C.3个 D.4个
C
√
×
√
×
√
典型例题
1.如何在操场上画一个半径是5 m 的圆?说出你的理由.
找一个钉子,钉在地上作为圆心,再找个5 m的软绳,绳子一端固定在钉子上,另一端固定一支粉笔,将绳子拉直绕钉子旋转一周粉笔画出的图形就是圆.
课堂练习
2.在△ABC中,∠C=90°,求证:A,B,C三点在同一个圆上.
?
A
C
B
O
课堂练习
1.下列语句中正确的有( )
①相等的圆心角所对的弧相等;
②在同圆或等圆中,相等的弦所对的弧相等;
③经过圆心的每一条直线都是圆的对称轴.
A.0个 B.1个 C.2个 D.3个
C
×
√
√
中考实题
2.如图,菱形ABCD的对角线AC和BD相交于点O,E,F,G,H分别为边AB,BC,CD,DA的中点,那么点E,F,G,H是否在同一个圆上?请说明理由.
?
中考实题
圆
定义
旋转定义
要画一个确定的圆,关键是确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
归纳新知
再 见
人教版数学九年级上册
24.1.1 圆
学习目标
1.巩固圆及其相关结论概念,深入理解圆的轴对称性和中心对称性.
2.掌握垂径定理,圆心角、弧、弦之间关系定理以及圆周角和圆心角关系定理.
3.进一步认识和理解圆的有关性质.
导入新知
圆是生活中常见的图形,许多物体都给我们以圆的形象.
1.观察以上图形,体验圆的和谐与美丽.请大家说说生活中还有哪些圆形?
2.请同学们在草稿纸上用圆规画圆,体验画圆的过程,想想圆是怎样形成的.
导入新知
我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?
合作探究
新知一
·
r
O
A
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.以点O为圆心的圆,记作“⊙O”,读作“圆O”,如下图所示.
固定的端点O叫做圆心,
线段OA叫做半径,一般用r表示.
合作探究
新知一
1.圆上各点到定点(圆心O)的距离都等于 .
2.到定点的距离等于定长的点都在 .
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
O
·
A
C
E
r
r
r
r
r
D
定长r
同一个圆上
圆的集合定义
从画圆的过程可以看出什么呢?
合作探究
新知一
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
同心圆
等圆
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
合作探究
新知一
例 矩形ABCD的对角线AC、BD相交于O.
求证:A、B、C、D在以O为圆心的同一圆上.
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AO=OC,OB=OD.
又∵AC=BD,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
合作探究
新知一
下列条件中,可以确定一个圆的是( )
D
A.半径为1 cm B.圆心在点O处
C.半径是1 cm,且经过点P D.圆心在点O处,且直径是2 cm
典型例题
·
C
O
A
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
注意
合作探究
新知二
O
A
B
O
A
B
圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
O
A
B
C
O
A
B
C
D
O
A
B
C
D
直径是最长的弦
合作探究
新知二
·
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
C
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
小于半圆的弧叫做劣弧,如图中的AC ;
(
大于半圆的弧叫做优弧,如图中的ABC.
(
合作探究
新知二
·
C
O
A
能够重合的两个圆叫做等圆.
·
C
O1
A
在同圆或等圆中,能够互相重合的弧叫做等弧.
等弧仅仅存在于同圆或者等圆中.
合作探究
新知二
注意
下列语句正确的有( )
①直径是弦;
②弦是直径;
③半径相等的两个半圆是等弧;
④长度相等的两条弧是等弧;
⑤半圆是弧,弧不一定是半圆.
A.1个 B.2个 C.3个 D.4个
C
√
×
√
×
√
典型例题
1.如何在操场上画一个半径是5 m 的圆?说出你的理由.
找一个钉子,钉在地上作为圆心,再找个5 m的软绳,绳子一端固定在钉子上,另一端固定一支粉笔,将绳子拉直绕钉子旋转一周粉笔画出的图形就是圆.
课堂练习
2.在△ABC中,∠C=90°,求证:A,B,C三点在同一个圆上.
?
A
C
B
O
课堂练习
1.下列语句中正确的有( )
①相等的圆心角所对的弧相等;
②在同圆或等圆中,相等的弦所对的弧相等;
③经过圆心的每一条直线都是圆的对称轴.
A.0个 B.1个 C.2个 D.3个
C
×
√
√
中考实题
2.如图,菱形ABCD的对角线AC和BD相交于点O,E,F,G,H分别为边AB,BC,CD,DA的中点,那么点E,F,G,H是否在同一个圆上?请说明理由.
?
中考实题
圆
定义
旋转定义
要画一个确定的圆,关键是确定圆心和半径
集合定义
同圆半径相等
有关
概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
能够互相重合的两段弧
归纳新知
再 见
同课章节目录
