人教版数学九年级下 册27.2.1三边法、两边及其夹角法课件(共17张ppt)
文档属性
| 名称 | 人教版数学九年级下 册27.2.1三边法、两边及其夹角法课件(共17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 562.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:46:12 | ||
图片预览




文档简介
回忆旧知 导入新课
一、同学们,通过前面的学习,我们已经掌握了两种判别三角形相似的方法?
方法一:利用定义判别
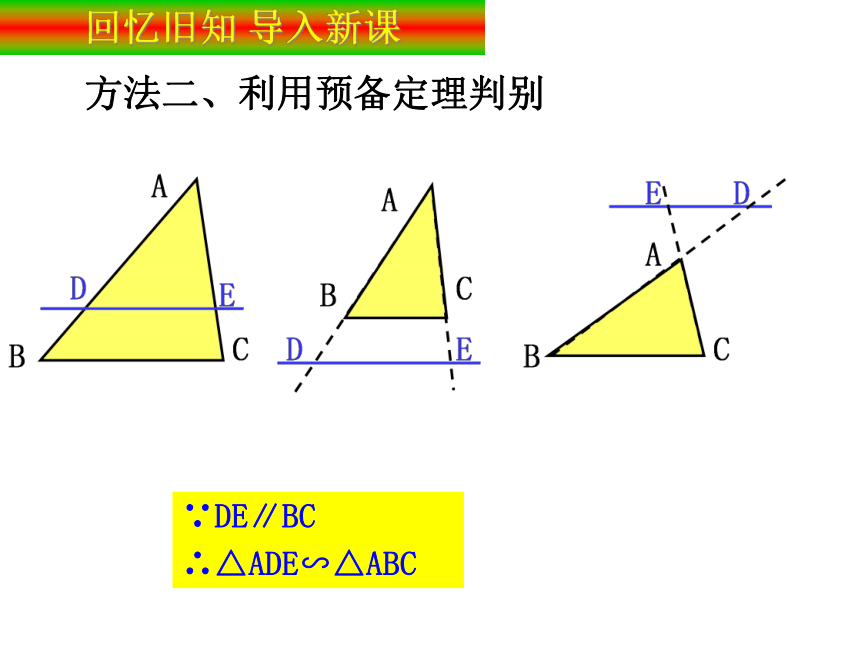
∵DE∥BC
∴△ADE∽△ABC
方法二、利用预备定理判别
回忆旧知 导入新课
类似于判定三角形全等的方法,我们能不能通过三边来判断两个三角形相似呢?有何猜想?
合作探究 形成新知
合作探究 形成新知
探究1
第一步: 猜想
第二步:画图验证猜想
第三步:逻辑推理证明
第四步:得出判定定理。
画△ABC, 使AB=4cm, BC=5cm, AC=6cm;
再画△A’B’C’,使A’B’=6cm, B’C’=7.5cm, A’C’=9cm.
这两个三角形相似吗?为什么?
探究1
第一步: 三边成比例的三角形相似
第二步:
D
E
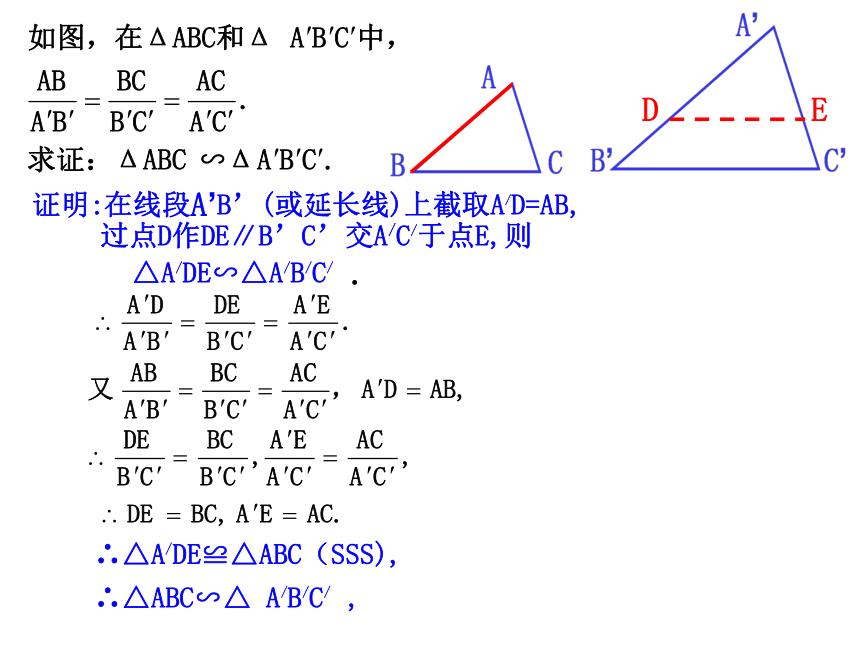
证明:在线段A’B’(或延长线)上截取A/D=AB,
过点D作DE∥B’C’交A/C/于点E,则△A/DE∽△A/B/C/ .
∴△A/DE≌△ABC(SSS),
∴△ABC∽△ A/B/C/ ,
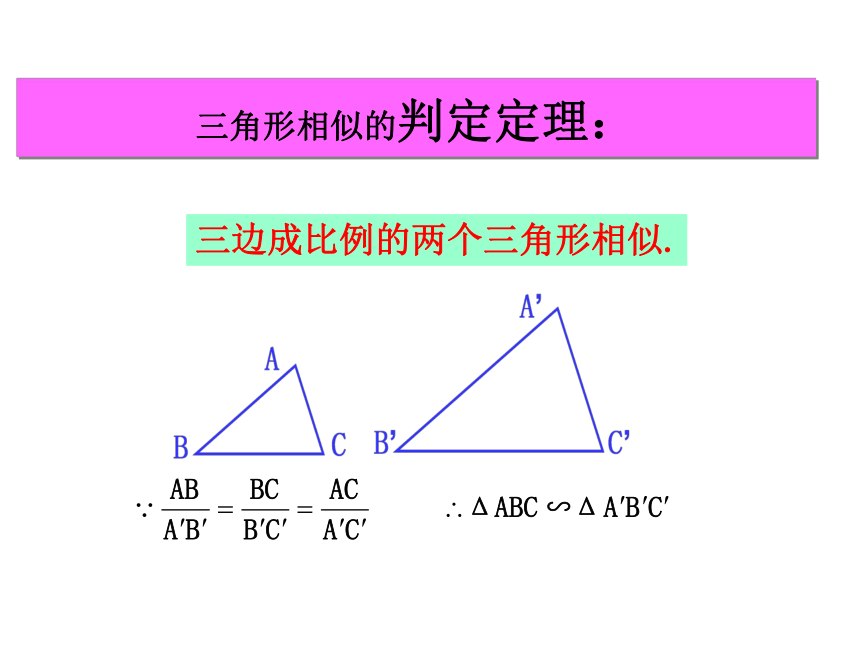
三角形相似的判定定理:
三边成比例的两个三角形相似.
探究2
画△ABC,使AB=4cm,∠A=60°,AC=6cm;
再画△A’B’C’,使A’B’=6cm, ∠A’=60°, A’C’=9cm.
这两个三角形相似吗?为什么?
类似于判定三角形全等的方法,我们能不能通过两边及其夹角判定三角形相似?
第一步:猜想出。。。。
第二步:画图验证
第三步:推理证明
D
E
证明:在边A’B’(或延长线)上截取A/D=AB,
过点D作DE∥B’C’交A/C/于点E,则△A/DE∽△A/B/C/ .
∴△A/DE≌△ABC(SAS),
∴△ABC∽△A/B/C/ ,
又∵∠ A=∠A’
三角形相似的判定定理:
两边成比例且夹角相等的两个三角形相似.
探究3
例1
试判定△ABC与A’B’C’是否相似,并说明理由.
(1) AB=4cm, BC=6cm, AC=8cm
A’B’=12cm,B’C’=18cm,A’C’=24cm
(2) ∠A=120°, AB=7cm, AC=14cm,
∠A’=120°,A’B’=3cm,A’C’=6cm;
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
例2
2、判断图中△AEB和△FEC是否相似?
54
30
36
45
E
A
F
C
B
检测一
检测二
这节课你有什么收获?
三边成比例的两个三角形相似.
两边成比例且夹角相等的两个角形相似.
检测三
4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?这个问题有其他答案吗?
4
5
6
2
一、同学们,通过前面的学习,我们已经掌握了两种判别三角形相似的方法?
方法一:利用定义判别
∵DE∥BC
∴△ADE∽△ABC
方法二、利用预备定理判别
回忆旧知 导入新课
类似于判定三角形全等的方法,我们能不能通过三边来判断两个三角形相似呢?有何猜想?
合作探究 形成新知
合作探究 形成新知
探究1
第一步: 猜想
第二步:画图验证猜想
第三步:逻辑推理证明
第四步:得出判定定理。
画△ABC, 使AB=4cm, BC=5cm, AC=6cm;
再画△A’B’C’,使A’B’=6cm, B’C’=7.5cm, A’C’=9cm.
这两个三角形相似吗?为什么?
探究1
第一步: 三边成比例的三角形相似
第二步:
D
E
证明:在线段A’B’(或延长线)上截取A/D=AB,
过点D作DE∥B’C’交A/C/于点E,则△A/DE∽△A/B/C/ .
∴△A/DE≌△ABC(SSS),
∴△ABC∽△ A/B/C/ ,
三角形相似的判定定理:
三边成比例的两个三角形相似.
探究2
画△ABC,使AB=4cm,∠A=60°,AC=6cm;
再画△A’B’C’,使A’B’=6cm, ∠A’=60°, A’C’=9cm.
这两个三角形相似吗?为什么?
类似于判定三角形全等的方法,我们能不能通过两边及其夹角判定三角形相似?
第一步:猜想出。。。。
第二步:画图验证
第三步:推理证明
D
E
证明:在边A’B’(或延长线)上截取A/D=AB,
过点D作DE∥B’C’交A/C/于点E,则△A/DE∽△A/B/C/ .
∴△A/DE≌△ABC(SAS),
∴△ABC∽△A/B/C/ ,
又∵∠ A=∠A’
三角形相似的判定定理:
两边成比例且夹角相等的两个三角形相似.
探究3
例1
试判定△ABC与A’B’C’是否相似,并说明理由.
(1) AB=4cm, BC=6cm, AC=8cm
A’B’=12cm,B’C’=18cm,A’C’=24cm
(2) ∠A=120°, AB=7cm, AC=14cm,
∠A’=120°,A’B’=3cm,A’C’=6cm;
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC-∠DAC=∠DAE-∠DAC
即∠BAD=∠CAE
例2
2、判断图中△AEB和△FEC是否相似?
54
30
36
45
E
A
F
C
B
检测一
检测二
这节课你有什么收获?
三边成比例的两个三角形相似.
两边成比例且夹角相等的两个角形相似.
检测三
4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?这个问题有其他答案吗?
4
5
6
2
