人教版数学九年级下册27.2.1 相似三角形的判定 第一课时课件(共22张ppt)
文档属性
| 名称 | 人教版数学九年级下册27.2.1 相似三角形的判定 第一课时课件(共22张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 22:12:34 | ||
图片预览





文档简介
【复习巩固】
1.什么叫做相似多边形?
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
2.相似多边形的性质:
(1)对应角相等;
(2)对应边的比相等.
相似三角形定义:我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。
思考:在相似多边形中,最简单的就是相似三角形.
对应角相等、对应边成比例的三角形叫做相似三角形.
相似三角形:
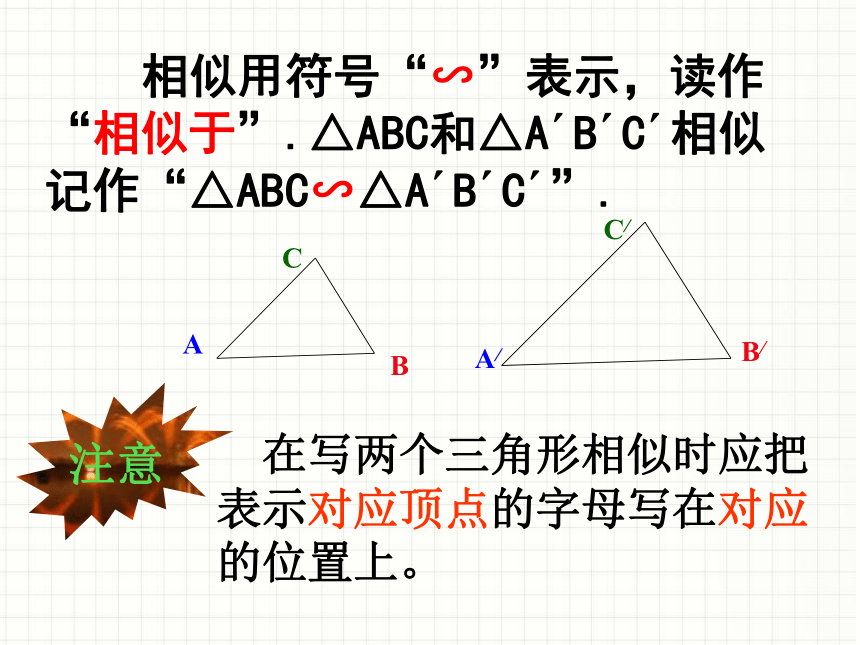
相似用符号“∽”表示,读作“相似于”.△ABC和△A?B?C?相似记作“△ABC∽△A?B?C?”.
C
A
B
A/
B/
C/
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上。
注意
用符号语言表示:
∵
∠A= ∠A' 、∠B= ∠B' 、∠C=C'
(相似三角形的定义可以作为三角形相似的一种判定方法)
则∠A= ∠A‘ 、∠B= ∠B' 、 ∠C= ∠ C'
反过来,如△ABC∽△A'B'C’
即相似三角形对应角相等,对应边成比例。
A
B
C
D
E
F
2cm
3cm
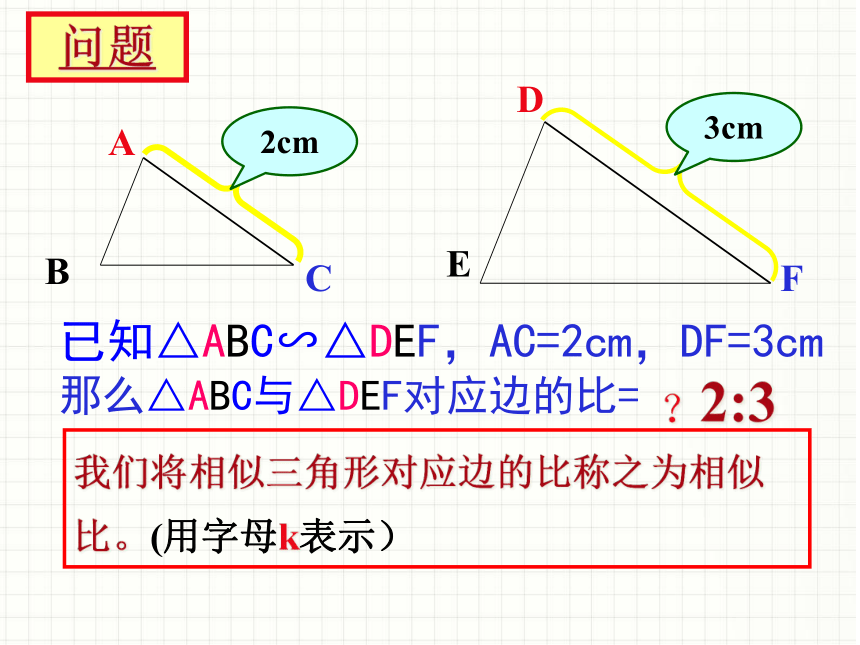
那么△ABC与△DEF对应边的比=
已知△ABC∽△DEF,AC=2cm,DF=3cm
我们将相似三角形对应边的比称之为相似比。(用字母k表示)
2:3
?
问题
C
A
B
A'
B'
C'
5cm
3cm
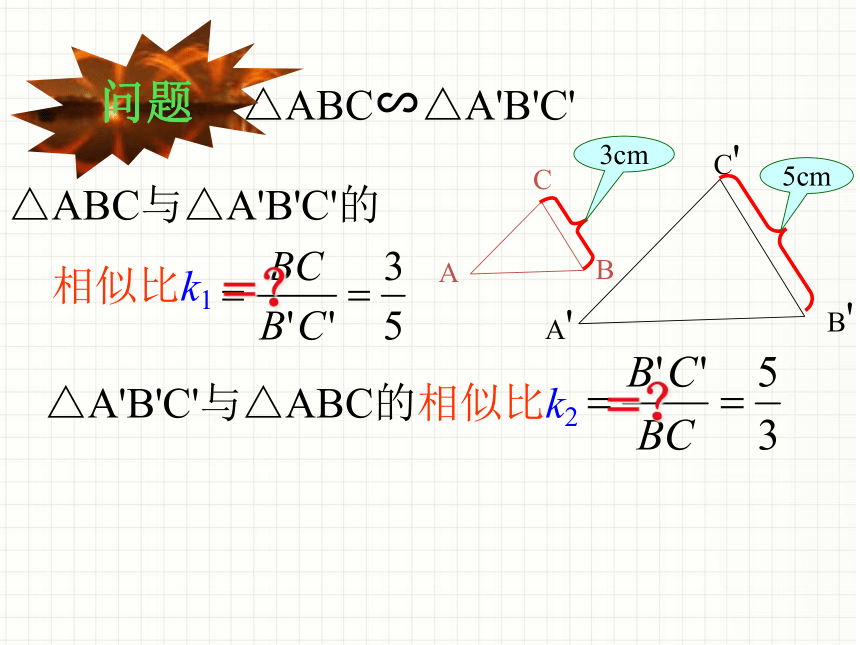
△ABC与△A'B'C'的
相似比k1
△A'B'C'与△ABC的相似比k2
=?
=?
△ABC∽△A'B'C'
问题
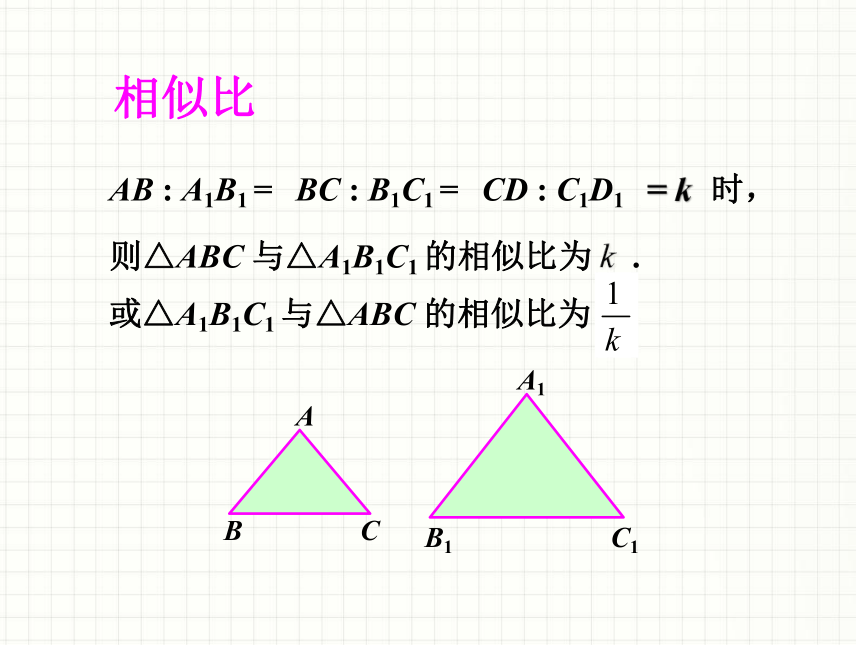
相似比
AB : A1B1 =
BC : B1C1 =
CD : C1D1
时,
A
B
C
A1
B1
C1
则△ABC 与△A1B1C1 的相似比为 k .
或△A1B1C1 与△ABC 的相似比为
A
B
C
D
E
F
l3
l4
l5
探究:平行线分线段成比例定理
如图,任意画两条直线 ,再画三条与 都相交的平行线 , 分别度量 在 上截得的两条线段AB, BC和在 上截得的两条线段DE, EF的长度, AB:BC与DE:EF相等吗?任意平移 , 再量度AB, BC, DE, EF的长度, AB :BC与DE :EF还相等吗?
l1
l2
猜想:
除此之外,还有其他对应线段成比例吗?
想一想:通过探究,你得到了什么规律呢?
事实上,当 时,可以得到 ,
还可以得到 , , 等等.
两条直线被一组平行线所截,所得的对应线段成比例.
平行线分线段成比例定理:
理解:平行线分线段成比例定理
A
B
C
D
E
F
l3
l4
l5
l1
l2
平行线分线段成比例定理的符号语言:
推出
两条直线被一组平行线所截,所得的对应线段城比例.
平行线分线段成比例定理:
A
B
D
C
F
E
G
如图,AB∥CD∥EF,AF与BE相交于点G,AG=2,GD=1,DF=5.
求 的值.
BC
CE
巩固练习
思考
C
A
B
C
D
E
F
l3
l4
l5
l1
l2
图1
探究:平行线分线段成比例定理的推论
如果把图1中 , 两条直线相交,交点A刚好落到 上, 如图2(1)所得的对应线段的比相等吗?依据是什么?
l1
l2
l3
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
平行线分线段成比例定理的推论:
A
B
C
E
F
l4
A
(D)
B
E
F
图2(1)
想一想:把 看作平行于
的边BC的直线.
通过探究,你能得出什么
规律?
l4
A
B
C
D
E
F
l3
l4
l5
l1
l2
A
B
C
E
D
图1
图2(2)
思考
探究:平行线分线段成比例定理的推论
如果把图1中 , 两条直线相交,交点A刚好落到 上, 如图2(2)所得的对应线段的比相等吗?依据是什么?
l1
l2
l4
平行于三角形一边的直线截其他两边的延长线,所得的对应线段成比例.
平行线分线段成比例定理的推论:
l4
l5
A
B
C
D
E
l3
l2
l1
想一想:把 看作平行于
的边BC的直线.
通过探究,你能得出什么
规律?
l3
A
B
C
E
D
A
B
C
D
E
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
归纳:平行线分线段成比例定理的推论
平行线分线段成比例定理的推论:
平行线分线段成比例定理的推论的数学符号语言:
A型
X型
AE
AC
AB
=
∵
AD
∵ DE∥BC
∵ DE∥BC
AE
AC
AB
=
∵
AD
A
B
C
D
E
——
——
1、判断题:
如图:DE∥BC, 下列各式是否正确:
D:
——
——
=
AD
AE
AB
AC
( )
C:
——
——
=
AD
AC
AE
AB
( )
B:
——
——
=
AD
BD
AE
CE
( )
A:
AD
AB
=
AE
AC
( )
A
B
C
E
D
2、填空题:
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
求:
——
2
—
5
练习1
A
B
C
D
E
已知:DE//BC, AB=15,AC=9,BD=4 . 求:AE=?
解:
∵ DE∥BC
AB AC
BD CE
∴
——
——
=
(推论)
15 9
4 CE
——
——
=
即
=
12
5
—
∴
CE
12
2
5
5
∴
AE= AC+CE=9+ =11—
—
练习2
练习3
A
A
B
C
D
E
1、如图: 已知 DE∥BC,
AB = 5, AC = 7 ,AD= 2,
求:AE的长.
如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
∴ AE=3.
解:
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
练习4
∵AC=4,EC=1,
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形.
△ABC与△DEF相似,记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
相似三角形的各对应角相等,各对应边对应成比例.
相似比就是它们的对应边的比.
课堂小结
一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例.
(关键要能熟练地找出对应线段)
三、要熟悉该定理的几种基本图形:
A
B
C
D
E
F
A
B
C
D
E
F
课堂小结
二、平行线分线段成比例定理的推论:
平行于三角形一边的直线截其他两边,所得的对应线段成比例. (关键要能熟练地找出对应线段)
A
B
C
D
E
F
课外作业
1.课本第31页第1题.
2.课本第42页第1、2题.
1.什么叫做相似多边形?
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
2.相似多边形的性质:
(1)对应角相等;
(2)对应边的比相等.
相似三角形定义:我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。
思考:在相似多边形中,最简单的就是相似三角形.
对应角相等、对应边成比例的三角形叫做相似三角形.
相似三角形:
相似用符号“∽”表示,读作“相似于”.△ABC和△A?B?C?相似记作“△ABC∽△A?B?C?”.
C
A
B
A/
B/
C/
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上。
注意
用符号语言表示:
∵
∠A= ∠A' 、∠B= ∠B' 、∠C=C'
(相似三角形的定义可以作为三角形相似的一种判定方法)
则∠A= ∠A‘ 、∠B= ∠B' 、 ∠C= ∠ C'
反过来,如△ABC∽△A'B'C’
即相似三角形对应角相等,对应边成比例。
A
B
C
D
E
F
2cm
3cm
那么△ABC与△DEF对应边的比=
已知△ABC∽△DEF,AC=2cm,DF=3cm
我们将相似三角形对应边的比称之为相似比。(用字母k表示)
2:3
?
问题
C
A
B
A'
B'
C'
5cm
3cm
△ABC与△A'B'C'的
相似比k1
△A'B'C'与△ABC的相似比k2
=?
=?
△ABC∽△A'B'C'
问题
相似比
AB : A1B1 =
BC : B1C1 =
CD : C1D1
时,
A
B
C
A1
B1
C1
则△ABC 与△A1B1C1 的相似比为 k .
或△A1B1C1 与△ABC 的相似比为
A
B
C
D
E
F
l3
l4
l5
探究:平行线分线段成比例定理
如图,任意画两条直线 ,再画三条与 都相交的平行线 , 分别度量 在 上截得的两条线段AB, BC和在 上截得的两条线段DE, EF的长度, AB:BC与DE:EF相等吗?任意平移 , 再量度AB, BC, DE, EF的长度, AB :BC与DE :EF还相等吗?
l1
l2
猜想:
除此之外,还有其他对应线段成比例吗?
想一想:通过探究,你得到了什么规律呢?
事实上,当 时,可以得到 ,
还可以得到 , , 等等.
两条直线被一组平行线所截,所得的对应线段成比例.
平行线分线段成比例定理:
理解:平行线分线段成比例定理
A
B
C
D
E
F
l3
l4
l5
l1
l2
平行线分线段成比例定理的符号语言:
推出
两条直线被一组平行线所截,所得的对应线段城比例.
平行线分线段成比例定理:
A
B
D
C
F
E
G
如图,AB∥CD∥EF,AF与BE相交于点G,AG=2,GD=1,DF=5.
求 的值.
BC
CE
巩固练习
思考
C
A
B
C
D
E
F
l3
l4
l5
l1
l2
图1
探究:平行线分线段成比例定理的推论
如果把图1中 , 两条直线相交,交点A刚好落到 上, 如图2(1)所得的对应线段的比相等吗?依据是什么?
l1
l2
l3
平行于三角形一边的直线截其他两边,所得的对应线段成比例.
平行线分线段成比例定理的推论:
A
B
C
E
F
l4
A
(D)
B
E
F
图2(1)
想一想:把 看作平行于
的边BC的直线.
通过探究,你能得出什么
规律?
l4
A
B
C
D
E
F
l3
l4
l5
l1
l2
A
B
C
E
D
图1
图2(2)
思考
探究:平行线分线段成比例定理的推论
如果把图1中 , 两条直线相交,交点A刚好落到 上, 如图2(2)所得的对应线段的比相等吗?依据是什么?
l1
l2
l4
平行于三角形一边的直线截其他两边的延长线,所得的对应线段成比例.
平行线分线段成比例定理的推论:
l4
l5
A
B
C
D
E
l3
l2
l1
想一想:把 看作平行于
的边BC的直线.
通过探究,你能得出什么
规律?
l3
A
B
C
E
D
A
B
C
D
E
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
归纳:平行线分线段成比例定理的推论
平行线分线段成比例定理的推论:
平行线分线段成比例定理的推论的数学符号语言:
A型
X型
AE
AC
AB
=
∵
AD
∵ DE∥BC
∵ DE∥BC
AE
AC
AB
=
∵
AD
A
B
C
D
E
——
——
1、判断题:
如图:DE∥BC, 下列各式是否正确:
D:
——
——
=
AD
AE
AB
AC
( )
C:
——
——
=
AD
AC
AE
AB
( )
B:
——
——
=
AD
BD
AE
CE
( )
A:
AD
AB
=
AE
AC
( )
A
B
C
E
D
2、填空题:
如图:DE∥BC,
已知:
2
=
——
AE
AC
—
5
=
——
AD
AB
求:
——
2
—
5
练习1
A
B
C
D
E
已知:DE//BC, AB=15,AC=9,BD=4 . 求:AE=?
解:
∵ DE∥BC
AB AC
BD CE
∴
——
——
=
(推论)
15 9
4 CE
——
——
=
即
=
12
5
—
∴
CE
12
2
5
5
∴
AE= AC+CE=9+ =11—
—
练习2
练习3
A
A
B
C
D
E
1、如图: 已知 DE∥BC,
AB = 5, AC = 7 ,AD= 2,
求:AE的长.
如图,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD.
∴ AE=3.
解:
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
练习4
∵AC=4,EC=1,
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形.
△ABC与△DEF相似,记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
相似三角形的各对应角相等,各对应边对应成比例.
相似比就是它们的对应边的比.
课堂小结
一、平行线分线段成比例定理:
三条平行线截两条直线,所得的对应线段成比例.
(关键要能熟练地找出对应线段)
三、要熟悉该定理的几种基本图形:
A
B
C
D
E
F
A
B
C
D
E
F
课堂小结
二、平行线分线段成比例定理的推论:
平行于三角形一边的直线截其他两边,所得的对应线段成比例. (关键要能熟练地找出对应线段)
A
B
C
D
E
F
课外作业
1.课本第31页第1题.
2.课本第42页第1、2题.
