沪科版九年级数学上册第22章相似形高分培优强化训练卷(Word版 含答案)
文档属性
| 名称 | 沪科版九年级数学上册第22章相似形高分培优强化训练卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 364.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-22 21:20:15 | ||
图片预览



文档简介
沪科版九年级数学上册第22章相似形高分培优强化训练卷
一、单选题
1.若,则等于( )
A.8
B.9
C.10
D.11
2.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12.在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为(
)
A.16
B.14
C.16或14
D.16或9
3.如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m
B.15m
C.20m
D.16m
4.按如下方法,将△ABC的三边缩小到原来的,如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
A.点O为位似中心且位似比为1:2
B.△ABC与△DEF是位似图形
C.△ABC与△DEF是相似图形
D.△ABC与△DEF的面积之比为4:1
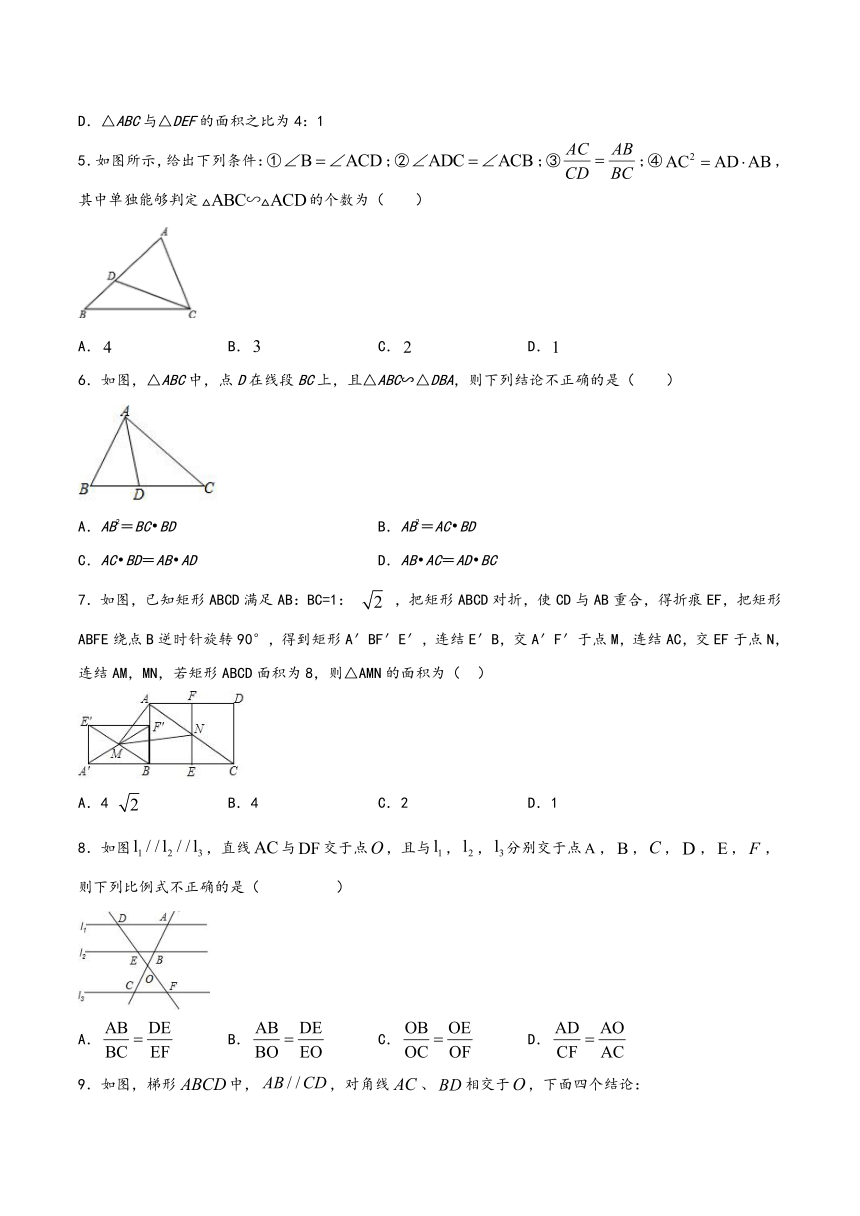
5.如图所示,给出下列条件:①;②;③;④,其中单独能够判定的个数为(
)
A.
B.
C.
D.
6.如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论不正确的是(
)
A.AB2=BCBD
B.AB2=ACBD
C.ACBD=ABAD
D.ABAC=ADBC
7.如图,已知矩形ABCD满足AB:BC=1:
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为(??
)
A.4
?????
B.4??????
C.2????
D.1
8.如图,直线与交于点,且与,,分别交于点,,,,,,则下列比例式不正确的是(
)
A.
B.
C.
D.
9.如图,梯形中,,对角线、相交于,下面四个结论:
①②③④.其中结论始终正确的有(
)
A.1个
B.2个
C.3个
D.4个
10.如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②OM=ON;③△OMN∽△OAD;④AN2+CM2=MN2,其中正确结论的个数是( )
A.1
B.2
C.3
D.4
11.如图,Rt△ABC中,∠C=90°,以点C为顶点向△ABC内作正方形DECF,使正方形的另三个顶点D、E、F分别在边AB,BC,AC上,若BC=6,AB=10,则正方形DECF的边长为( )
A.
B.
C.
D.
12.如图,Rt△ABC中,∠B=90?
,
BC=12,tanC=.
如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且;第二步从P1跳到BC边的P2(第2次落点)处,且;第三步从P2跳到AB边的P3(第3次落点)处,且;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为(
)
?
A.6?
B.5??
C.4?
D.3
二、填空题
13.如图,,若,,则________.
14.如图,是的斜边上异于、的一定点,过点作直线截交于点,使截得的与相似.已知,,,则________.
15.如图,点D、E在△ABC的边AB、AC上,请添加一个条件:____,使△ADE∽△ACB.
16.如图,将一张矩形纸片的边斜着向边对折,使点落在边上,记为,折痕为;再将边斜向下对折,使点落在上,记为,折痕为,,,则矩形纸片的面积为________.
17.如图,个边长为的相邻正方形的一边均在同一直线上,点,,,分别为边,,,,的中点,的面积为,的面积为,,的面积为,则________.(用含的式子表示)
三、解答题
18.如图,中,,,分别是,的中点,作且使,平分.
(1)判断的形状,并证明你的结论;
(2)求证:.
19.如图,有一块塑料矩形模板,长为,宽为,将你手中足够大的直角三角板的直角顶点落在边上(不与、重合),在上适当移动三角板顶点.
能否使你的三角板两直角边分别通过点与点?若能,请你求出这时的长;若不能,请说明理由;
再次移动三角板位置,使三角板顶点在上移动,直角边始终通过点,另一直
角边与延长线交于点,与交于点,能否使?若能,请你求出这时的长;若不能,请你说明理由.
20.如图所示,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
21.如图,抛物线与x轴交于点A(﹣,
0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
22.如图,抛物线y=ax2-2ax+b经过点C(0,-),且与x轴交于点A、点B,若tanACO=.
(1)求此抛物线的解析式;
(2)若抛物线的顶点为M,点P是线段OB上一动点(不与点B重合),MPQ=45,射线PQ与线段BM交于点Q,当△MPQ为等腰三角形时,求点P的坐标.
试卷第1页,总3页
参考答案
1.C2.D3.B4.A5.B6.B7.C8.D9.B10.D11.B12.A
13.
14.或
15.∠1=∠C或∠2=∠B或AD∶AC=AE∶AB(答一个即可).
16.15
17.
18.(1)是等腰直角三角形
19.可以使三角板两直角边分别通过点与点,或;能.在时,.
20.(1)当t=2时,△CEF是等腰直角三角形;(2)当t为3或1.2时,以点E,C,F为顶点的三角形与△ACD相似.
21.(1)y=﹣x2+x+1;(2)S=﹣t2+t+;(3)点N的坐标为(1,2)
22.(1)y=x2-x-(2)当△MPQ为等腰三角形时,点P的坐标为(1,0)或(3-,0).
一、单选题
1.若,则等于( )
A.8
B.9
C.10
D.11
2.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12.在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为(
)
A.16
B.14
C.16或14
D.16或9
3.如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m
B.15m
C.20m
D.16m
4.按如下方法,将△ABC的三边缩小到原来的,如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
A.点O为位似中心且位似比为1:2
B.△ABC与△DEF是位似图形
C.△ABC与△DEF是相似图形
D.△ABC与△DEF的面积之比为4:1
5.如图所示,给出下列条件:①;②;③;④,其中单独能够判定的个数为(
)
A.
B.
C.
D.
6.如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论不正确的是(
)
A.AB2=BCBD
B.AB2=ACBD
C.ACBD=ABAD
D.ABAC=ADBC
7.如图,已知矩形ABCD满足AB:BC=1:
,把矩形ABCD对折,使CD与AB重合,得折痕EF,把矩形ABFE绕点B逆时针旋转90°,得到矩形A′BF′E′,连结E′B,交A′F′于点M,连结AC,交EF于点N,连结AM,MN,若矩形ABCD面积为8,则△AMN的面积为(??
)
A.4
?????
B.4??????
C.2????
D.1
8.如图,直线与交于点,且与,,分别交于点,,,,,,则下列比例式不正确的是(
)
A.
B.
C.
D.
9.如图,梯形中,,对角线、相交于,下面四个结论:
①②③④.其中结论始终正确的有(
)
A.1个
B.2个
C.3个
D.4个
10.如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,与AB交于点N,连接OM,ON,MN.下列四个结论:①△CNB≌△DMC;②OM=ON;③△OMN∽△OAD;④AN2+CM2=MN2,其中正确结论的个数是( )
A.1
B.2
C.3
D.4
11.如图,Rt△ABC中,∠C=90°,以点C为顶点向△ABC内作正方形DECF,使正方形的另三个顶点D、E、F分别在边AB,BC,AC上,若BC=6,AB=10,则正方形DECF的边长为( )
A.
B.
C.
D.
12.如图,Rt△ABC中,∠B=90?
,
BC=12,tanC=.
如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且;第二步从P1跳到BC边的P2(第2次落点)处,且;第三步从P2跳到AB边的P3(第3次落点)处,且;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为(
)
?
A.6?
B.5??
C.4?
D.3
二、填空题
13.如图,,若,,则________.
14.如图,是的斜边上异于、的一定点,过点作直线截交于点,使截得的与相似.已知,,,则________.
15.如图,点D、E在△ABC的边AB、AC上,请添加一个条件:____,使△ADE∽△ACB.
16.如图,将一张矩形纸片的边斜着向边对折,使点落在边上,记为,折痕为;再将边斜向下对折,使点落在上,记为,折痕为,,,则矩形纸片的面积为________.
17.如图,个边长为的相邻正方形的一边均在同一直线上,点,,,分别为边,,,,的中点,的面积为,的面积为,,的面积为,则________.(用含的式子表示)
三、解答题
18.如图,中,,,分别是,的中点,作且使,平分.
(1)判断的形状,并证明你的结论;
(2)求证:.
19.如图,有一块塑料矩形模板,长为,宽为,将你手中足够大的直角三角板的直角顶点落在边上(不与、重合),在上适当移动三角板顶点.
能否使你的三角板两直角边分别通过点与点?若能,请你求出这时的长;若不能,请说明理由;
再次移动三角板位置,使三角板顶点在上移动,直角边始终通过点,另一直
角边与延长线交于点,与交于点,能否使?若能,请你求出这时的长;若不能,请你说明理由.
20.如图所示,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动.如果E,F同时出发,用t(0≤t≤6)秒表示运动的时间.
请解答下列问题:
(1)当t为何值时,△CEF是等腰直角三角形?
(2)当t为何值时,以点E,C,F为顶点的三角形与△ACD相似?
21.如图,抛物线与x轴交于点A(﹣,
0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
22.如图,抛物线y=ax2-2ax+b经过点C(0,-),且与x轴交于点A、点B,若tanACO=.
(1)求此抛物线的解析式;
(2)若抛物线的顶点为M,点P是线段OB上一动点(不与点B重合),MPQ=45,射线PQ与线段BM交于点Q,当△MPQ为等腰三角形时,求点P的坐标.
试卷第1页,总3页
参考答案
1.C2.D3.B4.A5.B6.B7.C8.D9.B10.D11.B12.A
13.
14.或
15.∠1=∠C或∠2=∠B或AD∶AC=AE∶AB(答一个即可).
16.15
17.
18.(1)是等腰直角三角形
19.可以使三角板两直角边分别通过点与点,或;能.在时,.
20.(1)当t=2时,△CEF是等腰直角三角形;(2)当t为3或1.2时,以点E,C,F为顶点的三角形与△ACD相似.
21.(1)y=﹣x2+x+1;(2)S=﹣t2+t+;(3)点N的坐标为(1,2)
22.(1)y=x2-x-(2)当△MPQ为等腰三角形时,点P的坐标为(1,0)或(3-,0).
