2020-2021学年苏科版八年级上册数学 一次函数6.1~6.3一次函数的图像 培优训练卷(word版有答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级上册数学 一次函数6.1~6.3一次函数的图像 培优训练卷(word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 412.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 06:53:56 | ||
图片预览




文档简介
2020-2021苏科版八年级上学期数学
一次函数6.1~6.3
培优训练卷
一、选择题
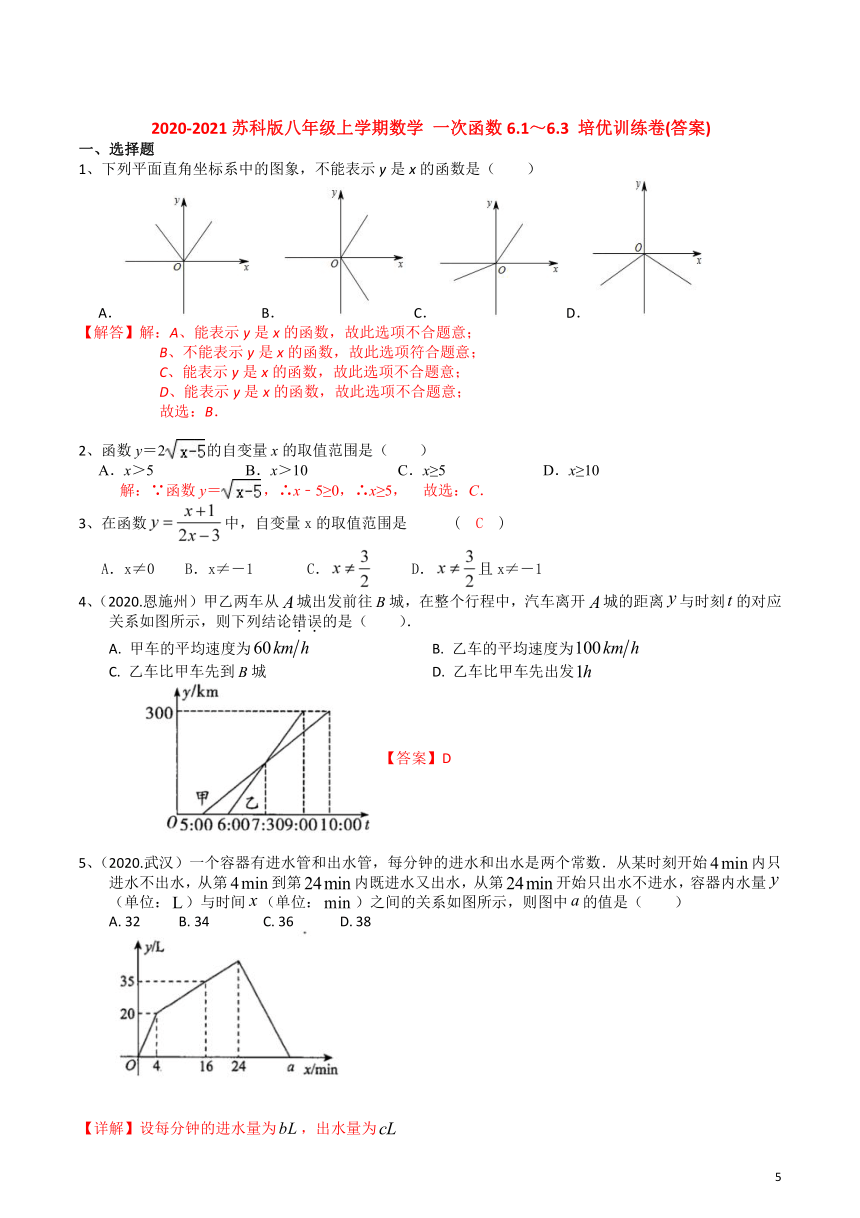
1、下列平面直角坐标系中的图象,不能表示y是x的函数是( )
A.
B.
C.
D.
2、函数y=2的自变量x的取值范围是( )
A.x>5
B.x>10
C.x≥5
D.x≥10
3、在函数中,自变量x的取值范围是
(
)
A.x≠0
B.x≠-1
C.
D.且x≠-1
4、(2020.恩施州)甲乙两车从城出发前往城,在整个行程中,汽车离开城的距离与时刻的对应关系如图所示,则下列结论错误的是(
).
A.
甲车的平均速度为
B.
乙车的平均速度为
C.
乙车比甲车先到城
D.
乙车比甲车先出发
(5)
5、(2020.武汉)一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始内只进水不出水,从第到第内既进水又出水,从第开始只出水不进水,容器内水量(单位:)与时间(单位:)之间的关系如图所示,则图中的值是(
)
A.
32
B.
34
C.
36
D.
38
6、下列函数;;③y=;;其中,是一次函数的有(
)
A.
1个
B.
2个
C.
3个
D.
4个
7、一次函数=x+b与在同一坐标系中的图像可能是(
)
B.
C.
D.
8、(2020.杭州)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
A.B.
C.D.
9、一次函数y=kx+b,y随x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是
(
)
A
B
C
D
10、两条直线与在同一直角坐标系中的图像可能是(
)
11、点P1
(x1,y1)和点P2(x2,y2)在同一直线y=-4x+3的图象上,且x1的关系是
(
)
A.y1>y2
B.y1C.y1=y2
D.y1>y2>0
12、已知点(-4,y1)、(2,y2)都在直线y=-x+2上,则y1与y2的大小关系是(
)
A.yl>y2
B.yl=y2
C.y1D.不能比较
13、已知一次函数y=kx+b,若k+b=1,则它的图象必过点
(
)
A.(-1,-1)
B.(1,1)
C.(-1,1)
D.(1,-1)
14、关于一次函数,下列结论正确的是(
)
A.图像经过点
B.图像经过第一、二、三象限
C.
y随的增大而增大
D.当时,
15、如图,在平面直角坐标系中,Q是直线y=x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点,连接,则的最小值为(
)
A.
B.
C.
D.
(17)
二、填空题
16、若函数y=
是正比例函数,则m的值是______
17、(2020.绥化)黑龙江省某企业用货车向乡镇运送农用物资,行驶2小时后,天空突然下起大雨,影响车辆行驶速度,货车行驶的路程与行驶时间的函数关系如图所示,2小时后货车的速度是________.
18、若函数y=﹣3x+a+2是正比例函数,则a= ,y随x的增大而 .
19、对于函数y=(k-3)x+k+3,
当k=____时,它是正比例函数;当k____时,它是一次函数.
20、已知函数y=2+a+2b是正比例函数,则a=________,b=________.
21、(2020.南京)将一次函数的图象绕原点逆时针旋转,所得到的图像对应的函数表达式是
22、(2020.常州)若一次函数的函数值y随自变量x增大而增大,则实数k的取值范围是__
23、已知直线y=kx+b与y=2x+1平行,且经过点(-3,4),则k=_____,b=_______
24、一条直线经过点,且与直线平行,则这条直线的函数表达式为_______
15、(2020.黔西南)如图,正比例函数的图象与一次函数y=﹣x+1的图象相交于点P,点P到x轴的距离
是2,则这个正比例函数的解析式是
.
26、一次函数y=3x+b的图像与两坐标轴围成的三角形面积是24,求b=_____
27、在直线上,且到坐标轴的距离为2的点的坐标是_____
28、直线y=x+4与x轴、y轴分别交于点A、B,M是y轴上一点
,若将?ABM沿AM折叠
,点B恰好落在x轴上
,
则点M的坐标为?
?
?
三、解答题
29、已知直线y=kx+b经过点(-1,4)和(2,1).
(1)求该直线的函数表达式.
(2)求该直线与x轴,y轴的交点坐标.
(3)求原点到该直线的距离
30、某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20
m3时,按2元/m3计费;月用水量超过20
m3时,其中的20
m3仍按2元/m3收费,超过部分按2.6元/m3计费.设每户家庭用用水量为x
m3时,应交水费y元.
(1)分别求出当0≤x≤20和x>20时,y与x的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份
四月份
五月份
六月份
交费金额
18元
33元
53元
小明家这个季度共用水多少立方米?
31、如图,直线l1的函数关系式为y=-3x+3,且l1与x轴交于点D.直线l2经过点A、B,直线l1、l2交于点C.(1)点D的坐标__________;
(2)求直线l2的函数关系式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP是△ADC的面积的2倍,求点P的坐标.
32、(2020.淮安)甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发小时后离甲地的路程为千米,图中折线表示接到通知前与之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为
千米/小时;
(2)求线段所表示的与之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.
33、(2020.河南)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身(次),按照方案一所需费用为,(元),且;按照方案二所需费用为(元)
,且其函数图象如图所示.
(1)求和的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和的值;
(3)八年级学生小华计划暑期前往该俱乐部健身次,应选择哪种方案所需费用更少?说明理由.
34、(2020.深圳)端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元
(1)肉粽和蜜枣粽的进货单价分别是多少元?
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?
2020-2021苏科版八年级上学期数学
一次函数6.1~6.3
培优训练卷(答案)
一、选择题
1、下列平面直角坐标系中的图象,不能表示y是x的函数是( )
A.
B.
C.
D.
【解答】解:A、能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项符合题意;
C、能表示y是x的函数,故此选项不合题意;
D、能表示y是x的函数,故此选项不合题意;
故选:B.
2、函数y=2的自变量x的取值范围是( )
A.x>5
B.x>10
C.x≥5
D.x≥10
解:∵函数y=,∴x﹣5≥0,∴x≥5,
故选:C.
3、在函数中,自变量x的取值范围是
(
C
)
A.x≠0
B.x≠-1
C.
D.且x≠-1
4、(2020.恩施州)甲乙两车从城出发前往城,在整个行程中,汽车离开城的距离与时刻的对应关系如图所示,则下列结论错误的是(
).
A.
甲车的平均速度为
B.
乙车的平均速度为
C.
乙车比甲车先到城
D.
乙车比甲车先出发
【答案】D
5、(2020.武汉)一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始内只进水不出水,从第到第内既进水又出水,从第开始只出水不进水,容器内水量(单位:)与时间(单位:)之间的关系如图所示,则图中的值是(
)
A.
32
B.
34
C.
36
D.
38
【详解】设每分钟的进水量为,出水量为
由第一段函数图象可知,
由第二段函数图象可知,,
即,
解得
则当时,
因此,,
解得,
故选:C.
6、下列函数;;③y=;;其中,是一次函数的有(
C
)
A.
1个
B.
2个
C.
3个
D.
4个
7、一次函数=x+b与在同一坐标系中的图像可能是(
C
)
B.
C.
D.
8、(2020.杭州)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
A.B.
C.D.
【解答】解:∵函数y=ax+a(a≠0)的图象过点P(1,2),∴2=a+a,解得a=1,
∴y=x+1,∴直线交y轴的正半轴,且过点(1,2),
故选:A.
9、一次函数y=kx+b,y随x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是
(
A
)
A
B
C
D
10、两条直线与在同一直角坐标系中的图像可能是(
A
)
11、点P1
(x1,y1)和点P2(x2,y2)在同一直线y=-4x+3的图象上,且x1的关系是
(
A
)
A.y1>y2
B.y1C.y1=y2
D.y1>y2>0
12、已知点(-4,y1)、(2,y2)都在直线y=-x+2上,则y1与y2的大小关系是(
A
)
A.yl>y2
B.yl=y2
C.y1D.不能比较
13、已知一次函数y=kx+b,若k+b=1,则它的图象必过点
(
B
)
A.(-1,-1)
B.(1,1)
C.(-1,1)
D.(1,-1)
14、关于一次函数,下列结论正确的是(
D
)
A.图像经过点
B.图像经过第一、二、三象限
C.
y随的增大而增大
D.当时,
15、如图,在平面直角坐标系中,Q是直线y=x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点,连接,则的最小值为(
)
A.
B.
C.
D.
【答案】B
二、填空题
16、若函数y=
是正比例函数,则m的值是___-2___
17、(2020.绥化)黑龙江省某企业用货车向乡镇运送农用物资,行驶2小时后,天空突然下起大雨,影响车辆行驶速度,货车行驶的路程与行驶时间的函数关系如图所示,2小时后货车的速度是___65_____.
18、若函数y=﹣3x+a+2是正比例函数,则a= ,y随x的增大而 .
【解答】解:∵函数y=﹣3x+a+2是正比例函数,
∴a+2=0,解得:a=﹣2,
∵﹣3<0,∴y随x的增大而减小.
故答案为:﹣2,减小.
19、对于函数y=(k-3)x+k+3,
当k=____时,它是正比例函数;当k____时,它是一次函数.
答案:-3
≠3
20、已知函数y=2+a+2b是正比例函数,则a=________,b=________.
答案:
-
21、(2020.南京)将一次函数的图象绕原点逆时针旋转,所得到的图像对应的函数表达式是
y=x+2
22、(2020.常州)若一次函数的函数值y随自变量x增大而增大,则实数k的取值范围是__k>0
23、已知直线y=kx+b与y=2x+1平行,且经过点(-3,4),则k=__2___,b=____10___
24、一条直线经过点,且与直线平行,则这条直线的函数表达式为__y=-3x+5_____
15、(2020.黔西南)如图,正比例函数的图象与一次函数y=﹣x+1的图象相交于点P,点P到x轴的距离
是2,则这个正比例函数的解析式是
.
【解答】解:∵点P到x轴的距离为2,∴点P的纵坐标为2,
∵点P在一次函数y=﹣x+1上,∴2=﹣x+1,得x=﹣1,
∴点P的坐标为(﹣1,2),
设正比例函数解析式为y=kx,
则2=﹣k,得k=﹣2,
∴正比例函数解析式为y=﹣2x,
故答案为:y=﹣2x.
26、一次函数y=3x+b的图像与两坐标轴围成的三角形面积是24,求b=__12____
27、在直线上,且到坐标轴的距离为2的点的坐标是_(2,2)或(-2,0)或(-6,-2)____
28、直线y=x+4与x轴、y轴分别交于点A、B,M是y轴上一点
,若将?ABM沿AM折叠
,点B恰好落在x轴上
,
则点M的坐标为?
(0,)或(0,-6)?
?
三、解答题
29、已知直线y=kx+b经过点(-1,4)和(2,1).
(1)求该直线的函数表达式.
(2)求该直线与x轴,y轴的交点坐标.
(3)求原点到该直线的距离
答案:(1)y=-x+3
(2)(3,0),(0,3)
(3)
30、某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20
m3时,按2元/m3计费;月用水量超过20
m3时,其中的20
m3仍按2元/m3收费,超过部分按2.6元/m3计费.设每户家庭用用水量为x
m3时,应交水费y元.
(1)分别求出当0≤x≤20和x>20时,y与x的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份
四月份
五月份
六月份
交费金额
18元
33元
53元
小明家这个季度共用水多少立方米?
答案:(1)当0≤x≤20时,y=2x,
当x>20时,y=2×20+2.6(x-20)=2.6x-12,
(2)∵四、五月份的水费都不超过40元,∴0≤x≤20,
y=2x=18时,x=9,
y=2x=33时,x=16.5,
∵六月份的水费都超过40元,∴x>20,
y=2.6x-12=53,x=25
∴小明家这个季度共用水9+16.5+25=50.5(立方米)
31、如图,直线l1的函数关系式为y=-3x+3,且l1与x轴交于点D.直线l2经过点A、B,直线l1、l2交于点C.
(1)点D的坐标__________;
(2)求直线l2的函数关系式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP是△ADC的面积的2倍,求点P的坐标.
答案:
(1)D(1,0)
(2)y=x-6
(3)
(4)(8,6)或(0,-6)
32、(2020.淮安)甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发小时后离甲地的路程为千米,图中折线表示接到通知前与之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为
千米/小时;
(2)求线段所表示的与之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.
【详解】解:(1)由图象可知,休息前汽车行驶的速度为千米/小时;
故答案为:80;
(2)休息后按原速继续前进行驶的时间为:(小时),
∴点E的坐标为(3.5,240),
设线段DE所表示的y与x之间的函数表达式为,
则:,解得,
∴线段DE所表示的y与x之间的函数表达式为;
(3)接到通知后,汽车仍按原速行驶,
则全程所需时间为:(小时),
从早上8点到中午12点需要12-8=4(小时),
∵4.125>4,
所以接到通知后,汽车仍按原速行驶不能准时到达.
33、(2020.河南)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身(次),按照方案一所需费用为,(元),且;按照方案二所需费用为(元)
,且其函数图象如图所示.
(1)求和的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和的值;
(3)八年级学生小华计划暑期前往该俱乐部健身次,应选择哪种方案所需费用更少?说明理由.
【详解】解:(1)由图象可得:经过(0,30)和(10,180)两点,代入函数关系式可得:,解得:,即k1=15,b=30,
k1=15表示的是每次健身费用按六折优惠是15元,
b=30表示购买一张学生暑期专享卡的费用是30元;
(2)设打折前的每次健身费用为a元,
由题意得:0.6a=15,解得:a=25,
即打折前的每次健身费用为25元,
k2表示每次健身按八折优惠的费用,故k2=25×0.8=20;
(3)由(1)(2)得:,,
当小华健身次即x=8时,
,,
∵150<160,
∴方案一所需费用更少,
答:方案一所需费用更少.
34、(2020.深圳)端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元
(1)肉粽和蜜枣粽的进货单价分别是多少元?
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?
解:(1)设肉粽和蜜枣粽的进货单价分别为x,y元,则根据题意可得:
,
解此方程组得:
答:肉粽得进货单价为10元,蜜枣粽得进货单价为4元
(2)设第二批购进肉粽t个,第二批粽子得利润为W,则
∵k=2>0,
∴W随t的增大而增大。
由题意,解得
∴当t=200时,第二批粽子由最大利润,最大利润
答:第二批购进肉粽200个时,全部售完后,第二批粽子获得利润最大,最大利润为1000元。
一次函数6.1~6.3
培优训练卷
一、选择题
1、下列平面直角坐标系中的图象,不能表示y是x的函数是( )
A.
B.
C.
D.
2、函数y=2的自变量x的取值范围是( )
A.x>5
B.x>10
C.x≥5
D.x≥10
3、在函数中,自变量x的取值范围是
(
)
A.x≠0
B.x≠-1
C.
D.且x≠-1
4、(2020.恩施州)甲乙两车从城出发前往城,在整个行程中,汽车离开城的距离与时刻的对应关系如图所示,则下列结论错误的是(
).
A.
甲车的平均速度为
B.
乙车的平均速度为
C.
乙车比甲车先到城
D.
乙车比甲车先出发
(5)
5、(2020.武汉)一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始内只进水不出水,从第到第内既进水又出水,从第开始只出水不进水,容器内水量(单位:)与时间(单位:)之间的关系如图所示,则图中的值是(
)
A.
32
B.
34
C.
36
D.
38
6、下列函数;;③y=;;其中,是一次函数的有(
)
A.
1个
B.
2个
C.
3个
D.
4个
7、一次函数=x+b与在同一坐标系中的图像可能是(
)
B.
C.
D.
8、(2020.杭州)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
A.B.
C.D.
9、一次函数y=kx+b,y随x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是
(
)
A
B
C
D
10、两条直线与在同一直角坐标系中的图像可能是(
)
11、点P1
(x1,y1)和点P2(x2,y2)在同一直线y=-4x+3的图象上,且x1
(
)
A.y1>y2
B.y1
D.y1>y2>0
12、已知点(-4,y1)、(2,y2)都在直线y=-x+2上,则y1与y2的大小关系是(
)
A.yl>y2
B.yl=y2
C.y1
13、已知一次函数y=kx+b,若k+b=1,则它的图象必过点
(
)
A.(-1,-1)
B.(1,1)
C.(-1,1)
D.(1,-1)
14、关于一次函数,下列结论正确的是(
)
A.图像经过点
B.图像经过第一、二、三象限
C.
y随的增大而增大
D.当时,
15、如图,在平面直角坐标系中,Q是直线y=x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点,连接,则的最小值为(
)
A.
B.
C.
D.
(17)
二、填空题
16、若函数y=
是正比例函数,则m的值是______
17、(2020.绥化)黑龙江省某企业用货车向乡镇运送农用物资,行驶2小时后,天空突然下起大雨,影响车辆行驶速度,货车行驶的路程与行驶时间的函数关系如图所示,2小时后货车的速度是________.
18、若函数y=﹣3x+a+2是正比例函数,则a= ,y随x的增大而 .
19、对于函数y=(k-3)x+k+3,
当k=____时,它是正比例函数;当k____时,它是一次函数.
20、已知函数y=2+a+2b是正比例函数,则a=________,b=________.
21、(2020.南京)将一次函数的图象绕原点逆时针旋转,所得到的图像对应的函数表达式是
22、(2020.常州)若一次函数的函数值y随自变量x增大而增大,则实数k的取值范围是__
23、已知直线y=kx+b与y=2x+1平行,且经过点(-3,4),则k=_____,b=_______
24、一条直线经过点,且与直线平行,则这条直线的函数表达式为_______
15、(2020.黔西南)如图,正比例函数的图象与一次函数y=﹣x+1的图象相交于点P,点P到x轴的距离
是2,则这个正比例函数的解析式是
.
26、一次函数y=3x+b的图像与两坐标轴围成的三角形面积是24,求b=_____
27、在直线上,且到坐标轴的距离为2的点的坐标是_____
28、直线y=x+4与x轴、y轴分别交于点A、B,M是y轴上一点
,若将?ABM沿AM折叠
,点B恰好落在x轴上
,
则点M的坐标为?
?
?
三、解答题
29、已知直线y=kx+b经过点(-1,4)和(2,1).
(1)求该直线的函数表达式.
(2)求该直线与x轴,y轴的交点坐标.
(3)求原点到该直线的距离
30、某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20
m3时,按2元/m3计费;月用水量超过20
m3时,其中的20
m3仍按2元/m3收费,超过部分按2.6元/m3计费.设每户家庭用用水量为x
m3时,应交水费y元.
(1)分别求出当0≤x≤20和x>20时,y与x的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份
四月份
五月份
六月份
交费金额
18元
33元
53元
小明家这个季度共用水多少立方米?
31、如图,直线l1的函数关系式为y=-3x+3,且l1与x轴交于点D.直线l2经过点A、B,直线l1、l2交于点C.(1)点D的坐标__________;
(2)求直线l2的函数关系式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP是△ADC的面积的2倍,求点P的坐标.
32、(2020.淮安)甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发小时后离甲地的路程为千米,图中折线表示接到通知前与之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为
千米/小时;
(2)求线段所表示的与之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.
33、(2020.河南)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身(次),按照方案一所需费用为,(元),且;按照方案二所需费用为(元)
,且其函数图象如图所示.
(1)求和的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和的值;
(3)八年级学生小华计划暑期前往该俱乐部健身次,应选择哪种方案所需费用更少?说明理由.
34、(2020.深圳)端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元
(1)肉粽和蜜枣粽的进货单价分别是多少元?
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?
2020-2021苏科版八年级上学期数学
一次函数6.1~6.3
培优训练卷(答案)
一、选择题
1、下列平面直角坐标系中的图象,不能表示y是x的函数是( )
A.
B.
C.
D.
【解答】解:A、能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项符合题意;
C、能表示y是x的函数,故此选项不合题意;
D、能表示y是x的函数,故此选项不合题意;
故选:B.
2、函数y=2的自变量x的取值范围是( )
A.x>5
B.x>10
C.x≥5
D.x≥10
解:∵函数y=,∴x﹣5≥0,∴x≥5,
故选:C.
3、在函数中,自变量x的取值范围是
(
C
)
A.x≠0
B.x≠-1
C.
D.且x≠-1
4、(2020.恩施州)甲乙两车从城出发前往城,在整个行程中,汽车离开城的距离与时刻的对应关系如图所示,则下列结论错误的是(
).
A.
甲车的平均速度为
B.
乙车的平均速度为
C.
乙车比甲车先到城
D.
乙车比甲车先出发
【答案】D
5、(2020.武汉)一个容器有进水管和出水管,每分钟的进水和出水是两个常数.从某时刻开始内只进水不出水,从第到第内既进水又出水,从第开始只出水不进水,容器内水量(单位:)与时间(单位:)之间的关系如图所示,则图中的值是(
)
A.
32
B.
34
C.
36
D.
38
【详解】设每分钟的进水量为,出水量为
由第一段函数图象可知,
由第二段函数图象可知,,
即,
解得
则当时,
因此,,
解得,
故选:C.
6、下列函数;;③y=;;其中,是一次函数的有(
C
)
A.
1个
B.
2个
C.
3个
D.
4个
7、一次函数=x+b与在同一坐标系中的图像可能是(
C
)
B.
C.
D.
8、(2020.杭州)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
A.B.
C.D.
【解答】解:∵函数y=ax+a(a≠0)的图象过点P(1,2),∴2=a+a,解得a=1,
∴y=x+1,∴直线交y轴的正半轴,且过点(1,2),
故选:A.
9、一次函数y=kx+b,y随x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是
(
A
)
A
B
C
D
10、两条直线与在同一直角坐标系中的图像可能是(
A
)
11、点P1
(x1,y1)和点P2(x2,y2)在同一直线y=-4x+3的图象上,且x1
(
A
)
A.y1>y2
B.y1
D.y1>y2>0
12、已知点(-4,y1)、(2,y2)都在直线y=-x+2上,则y1与y2的大小关系是(
A
)
A.yl>y2
B.yl=y2
C.y1
13、已知一次函数y=kx+b,若k+b=1,则它的图象必过点
(
B
)
A.(-1,-1)
B.(1,1)
C.(-1,1)
D.(1,-1)
14、关于一次函数,下列结论正确的是(
D
)
A.图像经过点
B.图像经过第一、二、三象限
C.
y随的增大而增大
D.当时,
15、如图,在平面直角坐标系中,Q是直线y=x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点,连接,则的最小值为(
)
A.
B.
C.
D.
【答案】B
二、填空题
16、若函数y=
是正比例函数,则m的值是___-2___
17、(2020.绥化)黑龙江省某企业用货车向乡镇运送农用物资,行驶2小时后,天空突然下起大雨,影响车辆行驶速度,货车行驶的路程与行驶时间的函数关系如图所示,2小时后货车的速度是___65_____.
18、若函数y=﹣3x+a+2是正比例函数,则a= ,y随x的增大而 .
【解答】解:∵函数y=﹣3x+a+2是正比例函数,
∴a+2=0,解得:a=﹣2,
∵﹣3<0,∴y随x的增大而减小.
故答案为:﹣2,减小.
19、对于函数y=(k-3)x+k+3,
当k=____时,它是正比例函数;当k____时,它是一次函数.
答案:-3
≠3
20、已知函数y=2+a+2b是正比例函数,则a=________,b=________.
答案:
-
21、(2020.南京)将一次函数的图象绕原点逆时针旋转,所得到的图像对应的函数表达式是
y=x+2
22、(2020.常州)若一次函数的函数值y随自变量x增大而增大,则实数k的取值范围是__k>0
23、已知直线y=kx+b与y=2x+1平行,且经过点(-3,4),则k=__2___,b=____10___
24、一条直线经过点,且与直线平行,则这条直线的函数表达式为__y=-3x+5_____
15、(2020.黔西南)如图,正比例函数的图象与一次函数y=﹣x+1的图象相交于点P,点P到x轴的距离
是2,则这个正比例函数的解析式是
.
【解答】解:∵点P到x轴的距离为2,∴点P的纵坐标为2,
∵点P在一次函数y=﹣x+1上,∴2=﹣x+1,得x=﹣1,
∴点P的坐标为(﹣1,2),
设正比例函数解析式为y=kx,
则2=﹣k,得k=﹣2,
∴正比例函数解析式为y=﹣2x,
故答案为:y=﹣2x.
26、一次函数y=3x+b的图像与两坐标轴围成的三角形面积是24,求b=__12____
27、在直线上,且到坐标轴的距离为2的点的坐标是_(2,2)或(-2,0)或(-6,-2)____
28、直线y=x+4与x轴、y轴分别交于点A、B,M是y轴上一点
,若将?ABM沿AM折叠
,点B恰好落在x轴上
,
则点M的坐标为?
(0,)或(0,-6)?
?
三、解答题
29、已知直线y=kx+b经过点(-1,4)和(2,1).
(1)求该直线的函数表达式.
(2)求该直线与x轴,y轴的交点坐标.
(3)求原点到该直线的距离
答案:(1)y=-x+3
(2)(3,0),(0,3)
(3)
30、某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20
m3时,按2元/m3计费;月用水量超过20
m3时,其中的20
m3仍按2元/m3收费,超过部分按2.6元/m3计费.设每户家庭用用水量为x
m3时,应交水费y元.
(1)分别求出当0≤x≤20和x>20时,y与x的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
月份
四月份
五月份
六月份
交费金额
18元
33元
53元
小明家这个季度共用水多少立方米?
答案:(1)当0≤x≤20时,y=2x,
当x>20时,y=2×20+2.6(x-20)=2.6x-12,
(2)∵四、五月份的水费都不超过40元,∴0≤x≤20,
y=2x=18时,x=9,
y=2x=33时,x=16.5,
∵六月份的水费都超过40元,∴x>20,
y=2.6x-12=53,x=25
∴小明家这个季度共用水9+16.5+25=50.5(立方米)
31、如图,直线l1的函数关系式为y=-3x+3,且l1与x轴交于点D.直线l2经过点A、B,直线l1、l2交于点C.
(1)点D的坐标__________;
(2)求直线l2的函数关系式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP是△ADC的面积的2倍,求点P的坐标.
答案:
(1)D(1,0)
(2)y=x-6
(3)
(4)(8,6)或(0,-6)
32、(2020.淮安)甲、乙两地的路程为290千米,一辆汽车早上8:00从甲地出发,匀速向乙地行驶,途中休息一段时间后,按原速继续前进,当离甲地路程为240千米时接到通知,要求中午12:00准时到达乙地.设汽车出发小时后离甲地的路程为千米,图中折线表示接到通知前与之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度为
千米/小时;
(2)求线段所表示的与之间的函数表达式;
(3)接到通知后,汽车仍按原速行驶能否准时到达?请说明理由.
【详解】解:(1)由图象可知,休息前汽车行驶的速度为千米/小时;
故答案为:80;
(2)休息后按原速继续前进行驶的时间为:(小时),
∴点E的坐标为(3.5,240),
设线段DE所表示的y与x之间的函数表达式为,
则:,解得,
∴线段DE所表示的y与x之间的函数表达式为;
(3)接到通知后,汽车仍按原速行驶,
则全程所需时间为:(小时),
从早上8点到中午12点需要12-8=4(小时),
∵4.125>4,
所以接到通知后,汽车仍按原速行驶不能准时到达.
33、(2020.河南)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身(次),按照方案一所需费用为,(元),且;按照方案二所需费用为(元)
,且其函数图象如图所示.
(1)求和的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和的值;
(3)八年级学生小华计划暑期前往该俱乐部健身次,应选择哪种方案所需费用更少?说明理由.
【详解】解:(1)由图象可得:经过(0,30)和(10,180)两点,代入函数关系式可得:,解得:,即k1=15,b=30,
k1=15表示的是每次健身费用按六折优惠是15元,
b=30表示购买一张学生暑期专享卡的费用是30元;
(2)设打折前的每次健身费用为a元,
由题意得:0.6a=15,解得:a=25,
即打折前的每次健身费用为25元,
k2表示每次健身按八折优惠的费用,故k2=25×0.8=20;
(3)由(1)(2)得:,,
当小华健身次即x=8时,
,,
∵150<160,
∴方案一所需费用更少,
答:方案一所需费用更少.
34、(2020.深圳)端午节前夕,某商铺用620元购进50个肉粽和30个蜜枣粽,肉粽的进货单价比蜜枣粽的进货单价多6元
(1)肉粽和蜜枣粽的进货单价分别是多少元?
(2)由于粽子畅销,商铺决定再购进这两种粽子共300个,其中肉粽数量不多于蜜枣粽数量的2倍,且每种粽子的进货单价保持不变,若肉粽的销售单价为14元,蜜枣粽的销售单价为6元,试问第二批购进肉粽多少个时,全部售完后,第二批粽子获得利润最大?第二批粽子的最大利润是多少元?
解:(1)设肉粽和蜜枣粽的进货单价分别为x,y元,则根据题意可得:
,
解此方程组得:
答:肉粽得进货单价为10元,蜜枣粽得进货单价为4元
(2)设第二批购进肉粽t个,第二批粽子得利润为W,则
∵k=2>0,
∴W随t的增大而增大。
由题意,解得
∴当t=200时,第二批粽子由最大利润,最大利润
答:第二批购进肉粽200个时,全部售完后,第二批粽子获得利润最大,最大利润为1000元。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
