八年级上册数学(人教版)13.3.2:等边三角形 教学设计(表格式)
文档属性
| 名称 | 八年级上册数学(人教版)13.3.2:等边三角形 教学设计(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 152.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 08:41:57 | ||
图片预览



文档简介
课程基本信息
课题
等边三角形
教科书
书名:义务教育教科书
数学
八年级上册
出版社:人民教育出版社
出版日期:2013
年
6
月
教学目标
教学目标:探索并掌握等边三角形的性质及判定方法,
运用等边三角形的性质和判定进行简单计算和证明.
教学重点:等边三角形的性质与判定
教学难点:等边三角形的性质与判定
教学过程
时间
教学环节
主要师生活动
2
分钟
环节1:
复习旧知,引入新课
复习回顾1:等腰三角形的性质和判定
名称图形定义性质判定等腰
三角形有两边相等的三角形是等腰三角形两腰相等两条边相等等边对等角“三线合一”等角对等边轴对称图形
(1条或3条对称轴)
复习回顾2:三角形如何按边分类
在三角形的按边分类中,等边三角形是特殊的等腰三角形.
引入新知:等边三角形的定义
等边三角形的定义:三边都相等的三角形叫做等边三角形(正三角形).
符号语言:
∵AB=AC=BC,
∴△ABC是等边三角形.
8
分钟
环节2:
合作探究,类比学习
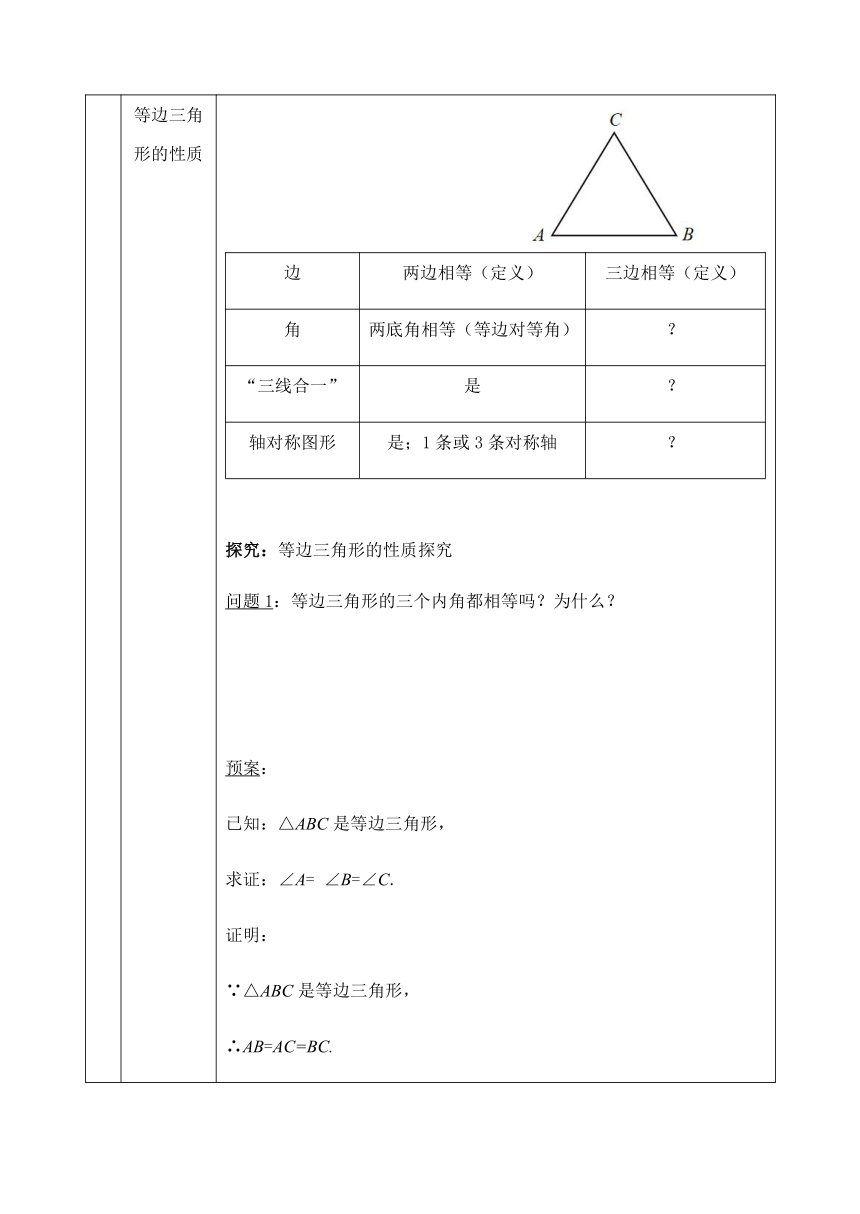
等边三角形的性质
类比:等边三角形是特殊的等腰三角形,所以等腰三角形的性质同样适用于等边三角形.但等边三角形还有哪些特殊的性质呢?让我们一起来探究一下吧.
等腰三角形的性质等边三角形的性质边两边相等(定义)三边相等(定义)角两底角相等(等边对等角)?“三线合一”是?轴对称图形是;1条或3条对称轴?
探究:等边三角形的性质探究
问题1:等边三角形的三个内角都相等吗?为什么?
预案:
已知:△ABC是等边三角形,
求证:∠A=
∠B=∠C.
证明:
∵△ABC是等边三角形,
∴AB=AC=BC.
∵AB=AC,
∴∠B=∠C
.(等边对等角)
同理
∠A=∠C
.
∴∠A=∠B=∠C.
进一步发现,每一个内角都等于60°.
∵
∠A+∠B+∠C=180°,
∴
∠A=
∠B=
∠C=60°.
等边三角形的性质(2):等边三角形的三个内角都相等,并且每一个角都等于60°.
问题2:等边三角形有“三线合一”的性质吗?为什么?
等边三角形的性质(3):等边三角形每条边上的中线、高和所对角的平分线都相互重合(“三线合一”).
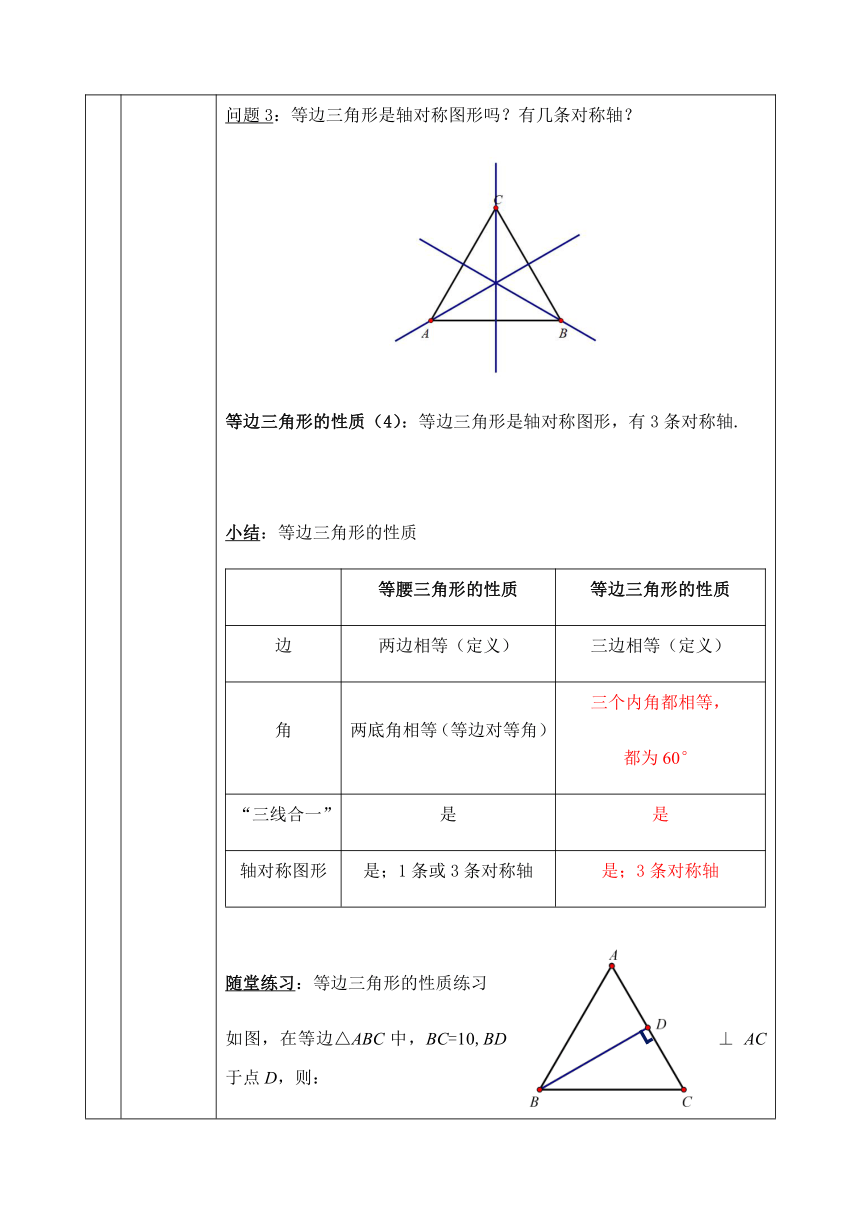
问题3:等边三角形是轴对称图形吗?有几条对称轴?
等边三角形的性质(4):等边三角形是轴对称图形,有3条对称轴.
小结:等边三角形的性质
等腰三角形的性质等边三角形的性质边两边相等(定义)三边相等(定义)角两底角相等(等边对等角)三个内角都相等,
都为60°“三线合一”是是轴对称图形是;1条或3条对称轴是;3条对称轴
随堂练习:等边三角形的性质练习
如图,在等边△ABC中,BC=10,BD⊥AC于点D,则:
AC=
;
(2)∠A=
;
(3)∠ABD=
,
AD=
.
答案:(1)10;
考查:等边三角形的性质(1)三边相等;
(2)60°;
考查:等边三角形的性质(2)等边三角形的三个内角都相等,并且每一个角都等于60°;
(3)30°,5
考查:等边三角形的性质(3)等边三角形每条边上的中线、高和所对角的平分线都相互重合(“三线合一”)
预案1:“三线合一”
预案2:三角形的内角和
6
分钟
环节3:
类比探究
等边三角形的判定方法
思考1:一个三角形满足什么条件是等边三角形?
思考2:一个等腰三角形满足什么条件是等边三角形?
预案(思考1):
已知:在△ABC
中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
证明:
∵ ∠A=∠B,
∠B=∠C,
∴ BC=AC,
AC=AB.(等角对等边)
∴ AB=BC=AC.
∴ △ABC是等边三角形.
预案(思考2):
有一个角是60°的等腰三角形是等边三角形.
分类讨论:
顶角是60°
有一个底角是60°
假若AB=AC,则∠B=∠C.
(1)当顶角∠A=60
°时,∠B=
∠C=
60
°,
∴
∠A=∠B=∠C=60
°.
∴
△ABC是等边三角形.
(2)当底角∠B=
60°时,∠C=60°,
∠A=180°-(60°+60°)=60°.
∴
∠A=∠B=∠C=60°.
∴
△ABC是等边三角形.
小结:等边三角形的判定方法
名称图形判定与边角关系等边三角形三条边都相等的三角形三个角都相等的三角形有一个角是60°的等腰三角形
8
分钟
环节4:
例题讲解,一题多解
如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
分析:
思路1
证明:
∵△ABC是等边三角形,
∴ ∠A
=∠B
=∠C.
∵ DE∥BC,
∴ ∠B
=∠ADE,∠C
=∠AED.
∴ ∠A=∠ADE
=∠AED.
∴ △ADE是等边三角形.
思路2
证明:
∵△ABC是等边三角形,
∴ ∠A
=∠B
=∠C=60°.
∵ DE∥BC,
∴ ∠B
=∠ADE,∠C
=∠AED.
∴ ∠ADE
=∠AED.
∴ AD
=AE.
∴ △ADE是等腰三角形.
∵
∠A
=60°,
∴ △ADE是等边三角形.
思路3
证明:∵△ABC是等边三角形,
∴ ∠A
=∠B
=∠C.
∵ DE∥BC,
∴ ∠B
=∠ADE,∠C
=∠AED.
∴ ∠A
=∠ADE,∠ADE
=∠AED.
∴ DE
=AE,AD
=AE.
即 AD
=AE
=DE.
∴ △ADE是等边三角形.
小结:
一题多解
此题中,思路1所对应的方法较思路2和3更加直接、简便.
1
分钟
环节5:
归纳小结
等边三角形性质三条边相等2.
三个内角都相等,都为60°3.
“三线合一”4.
轴对称图形(3条对称轴)判定定义(三条边相等)2.
三个角相等有一个角是60°的等腰三角形
课后作业
已知△ABC中,∠A=∠B=60°,AB=3
cm,
则
△ABC的周长____.
答案:9
cm
△ABC是等腰三角形,周长为15
cm且∠A=60°,则BC=_______.
答案:5
cm
3.
等边三角形两条高相交所成的钝角的度数是_______.
答案:120°
例题变式练习:
变式1:
△ABC是等边三角形,若点D,E
在边AB,AC
的延长线上,且
DE∥BC,结论还成立吗?
证明:∵ △ABC是等边三角形,
∴ ∠A=∠ABC=∠ACB.
∵ DE∥BC,
∴ ∠ABC
=∠ADE,
∠ACB
=∠AED.
∴ ∠A
=∠ADE
=∠AED.
∴ △ADE是等边三角形.
变式2:
△ABC是等边三角形,若点D,E
在边AC,AB
的反向延长线上,且
DE∥BC,结论还成立吗?
证明:∵ △ABC是等边三角形,
∴ ∠BAC
=∠B
=∠C.
∵ DE∥BC,
∴ ∠B
=∠E,
∠C
=∠D.
∵
∠BAC=∠DAE
∴ ∠DAE
=∠D
=∠E.
∴ △ADE是等边三角形.
变式3:
例题中,△ABC是等边三角形,若将条件DE∥BC改为AD=AE,
△ADE还是等边三角形吗?试说明理由.
证明:∵ AD=AE,
∴ △ADE是等腰三角形.
∵
△ABC是等边三角形,
∴ ∠A
=∠B
=∠C=60°.
∴ △ADE是等边三角形.
课题
等边三角形
教科书
书名:义务教育教科书
数学
八年级上册
出版社:人民教育出版社
出版日期:2013
年
6
月
教学目标
教学目标:探索并掌握等边三角形的性质及判定方法,
运用等边三角形的性质和判定进行简单计算和证明.
教学重点:等边三角形的性质与判定
教学难点:等边三角形的性质与判定
教学过程
时间
教学环节
主要师生活动
2
分钟
环节1:
复习旧知,引入新课
复习回顾1:等腰三角形的性质和判定
名称图形定义性质判定等腰
三角形有两边相等的三角形是等腰三角形两腰相等两条边相等等边对等角“三线合一”等角对等边轴对称图形
(1条或3条对称轴)
复习回顾2:三角形如何按边分类
在三角形的按边分类中,等边三角形是特殊的等腰三角形.
引入新知:等边三角形的定义
等边三角形的定义:三边都相等的三角形叫做等边三角形(正三角形).
符号语言:
∵AB=AC=BC,
∴△ABC是等边三角形.
8
分钟
环节2:
合作探究,类比学习
等边三角形的性质
类比:等边三角形是特殊的等腰三角形,所以等腰三角形的性质同样适用于等边三角形.但等边三角形还有哪些特殊的性质呢?让我们一起来探究一下吧.
等腰三角形的性质等边三角形的性质边两边相等(定义)三边相等(定义)角两底角相等(等边对等角)?“三线合一”是?轴对称图形是;1条或3条对称轴?
探究:等边三角形的性质探究
问题1:等边三角形的三个内角都相等吗?为什么?
预案:
已知:△ABC是等边三角形,
求证:∠A=
∠B=∠C.
证明:
∵△ABC是等边三角形,
∴AB=AC=BC.
∵AB=AC,
∴∠B=∠C
.(等边对等角)
同理
∠A=∠C
.
∴∠A=∠B=∠C.
进一步发现,每一个内角都等于60°.
∵
∠A+∠B+∠C=180°,
∴
∠A=
∠B=
∠C=60°.
等边三角形的性质(2):等边三角形的三个内角都相等,并且每一个角都等于60°.
问题2:等边三角形有“三线合一”的性质吗?为什么?
等边三角形的性质(3):等边三角形每条边上的中线、高和所对角的平分线都相互重合(“三线合一”).
问题3:等边三角形是轴对称图形吗?有几条对称轴?
等边三角形的性质(4):等边三角形是轴对称图形,有3条对称轴.
小结:等边三角形的性质
等腰三角形的性质等边三角形的性质边两边相等(定义)三边相等(定义)角两底角相等(等边对等角)三个内角都相等,
都为60°“三线合一”是是轴对称图形是;1条或3条对称轴是;3条对称轴
随堂练习:等边三角形的性质练习
如图,在等边△ABC中,BC=10,BD⊥AC于点D,则:
AC=
;
(2)∠A=
;
(3)∠ABD=
,
AD=
.
答案:(1)10;
考查:等边三角形的性质(1)三边相等;
(2)60°;
考查:等边三角形的性质(2)等边三角形的三个内角都相等,并且每一个角都等于60°;
(3)30°,5
考查:等边三角形的性质(3)等边三角形每条边上的中线、高和所对角的平分线都相互重合(“三线合一”)
预案1:“三线合一”
预案2:三角形的内角和
6
分钟
环节3:
类比探究
等边三角形的判定方法
思考1:一个三角形满足什么条件是等边三角形?
思考2:一个等腰三角形满足什么条件是等边三角形?
预案(思考1):
已知:在△ABC
中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
证明:
∵ ∠A=∠B,
∠B=∠C,
∴ BC=AC,
AC=AB.(等角对等边)
∴ AB=BC=AC.
∴ △ABC是等边三角形.
预案(思考2):
有一个角是60°的等腰三角形是等边三角形.
分类讨论:
顶角是60°
有一个底角是60°
假若AB=AC,则∠B=∠C.
(1)当顶角∠A=60
°时,∠B=
∠C=
60
°,
∴
∠A=∠B=∠C=60
°.
∴
△ABC是等边三角形.
(2)当底角∠B=
60°时,∠C=60°,
∠A=180°-(60°+60°)=60°.
∴
∠A=∠B=∠C=60°.
∴
△ABC是等边三角形.
小结:等边三角形的判定方法
名称图形判定与边角关系等边三角形三条边都相等的三角形三个角都相等的三角形有一个角是60°的等腰三角形
8
分钟
环节4:
例题讲解,一题多解
如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
分析:
思路1
证明:
∵△ABC是等边三角形,
∴ ∠A
=∠B
=∠C.
∵ DE∥BC,
∴ ∠B
=∠ADE,∠C
=∠AED.
∴ ∠A=∠ADE
=∠AED.
∴ △ADE是等边三角形.
思路2
证明:
∵△ABC是等边三角形,
∴ ∠A
=∠B
=∠C=60°.
∵ DE∥BC,
∴ ∠B
=∠ADE,∠C
=∠AED.
∴ ∠ADE
=∠AED.
∴ AD
=AE.
∴ △ADE是等腰三角形.
∵
∠A
=60°,
∴ △ADE是等边三角形.
思路3
证明:∵△ABC是等边三角形,
∴ ∠A
=∠B
=∠C.
∵ DE∥BC,
∴ ∠B
=∠ADE,∠C
=∠AED.
∴ ∠A
=∠ADE,∠ADE
=∠AED.
∴ DE
=AE,AD
=AE.
即 AD
=AE
=DE.
∴ △ADE是等边三角形.
小结:
一题多解
此题中,思路1所对应的方法较思路2和3更加直接、简便.
1
分钟
环节5:
归纳小结
等边三角形性质三条边相等2.
三个内角都相等,都为60°3.
“三线合一”4.
轴对称图形(3条对称轴)判定定义(三条边相等)2.
三个角相等有一个角是60°的等腰三角形
课后作业
已知△ABC中,∠A=∠B=60°,AB=3
cm,
则
△ABC的周长____.
答案:9
cm
△ABC是等腰三角形,周长为15
cm且∠A=60°,则BC=_______.
答案:5
cm
3.
等边三角形两条高相交所成的钝角的度数是_______.
答案:120°
例题变式练习:
变式1:
△ABC是等边三角形,若点D,E
在边AB,AC
的延长线上,且
DE∥BC,结论还成立吗?
证明:∵ △ABC是等边三角形,
∴ ∠A=∠ABC=∠ACB.
∵ DE∥BC,
∴ ∠ABC
=∠ADE,
∠ACB
=∠AED.
∴ ∠A
=∠ADE
=∠AED.
∴ △ADE是等边三角形.
变式2:
△ABC是等边三角形,若点D,E
在边AC,AB
的反向延长线上,且
DE∥BC,结论还成立吗?
证明:∵ △ABC是等边三角形,
∴ ∠BAC
=∠B
=∠C.
∵ DE∥BC,
∴ ∠B
=∠E,
∠C
=∠D.
∵
∠BAC=∠DAE
∴ ∠DAE
=∠D
=∠E.
∴ △ADE是等边三角形.
变式3:
例题中,△ABC是等边三角形,若将条件DE∥BC改为AD=AE,
△ADE还是等边三角形吗?试说明理由.
证明:∵ AD=AE,
∴ △ADE是等腰三角形.
∵
△ABC是等边三角形,
∴ ∠A
=∠B
=∠C=60°.
∴ △ADE是等边三角形.
