沪教版(上海)初中数学九年级第一学期 24.1 放缩与相似形 教案
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.1 放缩与相似形 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 91.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 08:44:47 | ||
图片预览

文档简介
放缩与相似形
概念:
一、相似图形:形状相同的图形
概念(1)图形的放大或缩小称为图形的放缩运动.
(2)把形状相同的两个图形称为相似形.
(3)如果两个多边形是相似图形,那么这两个多边形的对应角相等,各对应边的长度成比例(或各对应边长度的比值是相等的)
(三)相似图形的对应关系:
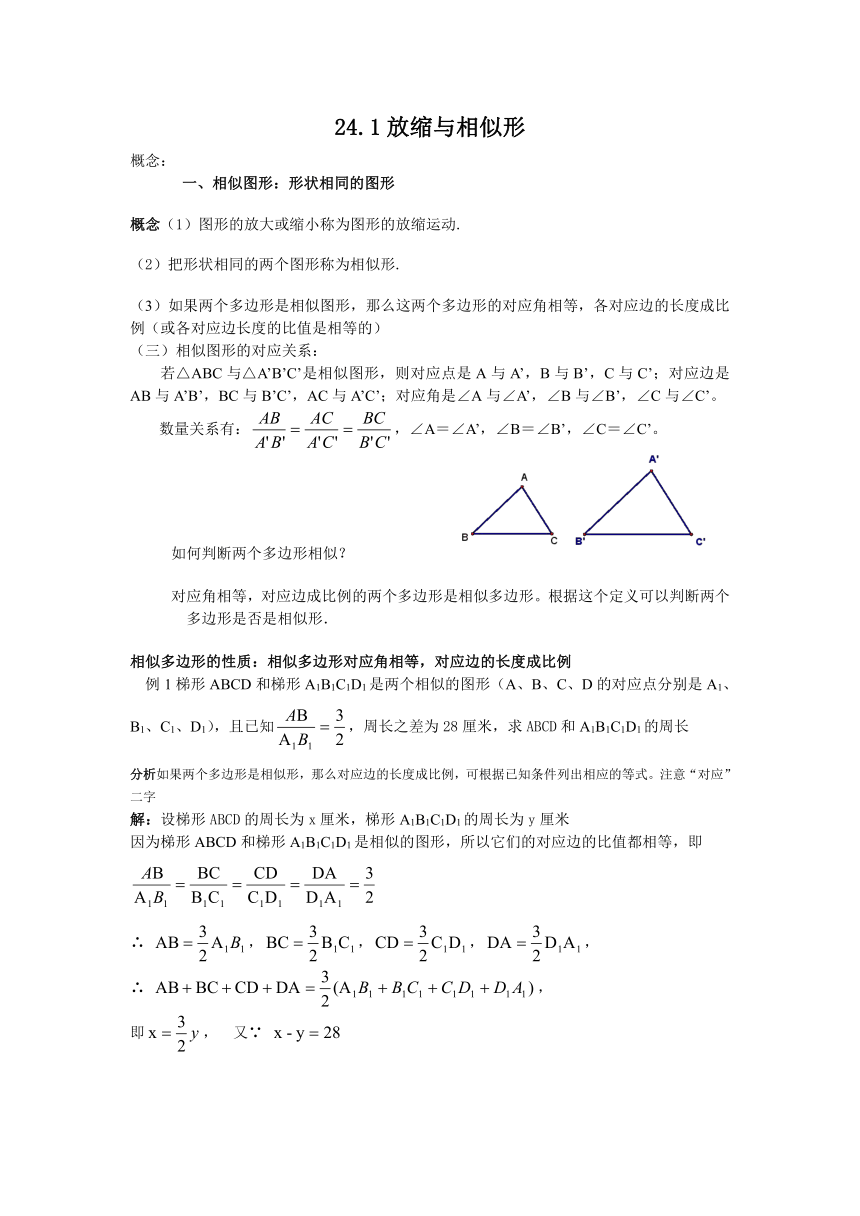
若△ABC与△A’B’C’是相似图形,则对应点是A与A’,B与B’,C与C’;对应边是AB与A’B’,BC与B’C’,AC与A’C’;对应角是∠A与∠A’,∠B与∠B’,∠C与∠C’。
数量关系有:,∠A=∠A’,∠B=∠B’,∠C=∠C’。
如何判断两个多边形相似?
对应角相等,对应边成比例的两个多边形是相似多边形。根据这个定义可以判断两个多边形是否是相似形.
相似多边形的性质:相似多边形对应角相等,对应边的长度成比例
例1梯形ABCD和梯形A1B1C1D1是两个相似的图形(A、B、C、D的对应点分别是A1、B1、C1、D1),且已知,周长之差为28厘米,求ABCD和A1B1C1D1的周长
分析如果两个多边形是相似形,那么对应边的长度成比例,可根据已知条件列出相应的等式。注意“对应”二字
解:设梯形ABCD的周长为x厘米,梯形A1B1C1D1的周长为y厘米
因为梯形ABCD和梯形A1B1C1D1是相似的图形,所以它们的对应边的比值都相等,即
∴
,,,,
∴
,
即,
又∵
解方程组
得
所以梯形ABCD的周长和梯形A1B1C1D1的周长分别为84厘米和56厘米
例2、如图24—1,矩形ABCD中,AB=2AD,线段EF=10.在EF上取一点M,分别以EM、MF为一边作矩形EMNH、矩形MFGN,使矩形MFGN与矩形ABCD相似,且点M与点A、点F与点B、点G与点C、点N与点D分别是对应顶点,令MN=x.求出矩形EMNH的面积S与x的函数关系式
解因为矩形MFGN与矩形ABCD是相似的图形,且点M与
点A、点F与点B、点G与点C、点N与点D分别是对应顶点,
∴
∵AB=2AD,MN=x
∴MF=2NM=2x
∴EM=10-2x
∴
二、比例线段:
【两条线段的比】两条线段长度的比
【比例线段】四条线段a,b,c,d中,如果(a:b=c:d),那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
线段d是a、b、c的第四比例项.
比例中项:如果作为比例线段的内项是两条相同的线段,即a:b=b:c,或a/b=b/c,那么线段b叫做线段a和c
的比例中项,他们有关系:
☆
比例基本性质:内项积等于外项积.
例3、已知a、b、c、d是四条线段,它们的长度如下,试判断它们是不是成比例线段?
(1)a=1mm,b=0.8cm,c=0.02cm,d=4cm;(2)cm,b=0.4cm,c=40cm,.
解:<统一单位>a=0.1cm,b=0.8cm,c=0.02cm,d=4cm
<最大乘最小,剩下两项乘>
∵dc=4×0.02=0.08,ab=0.1×0.8=0.08
∴
ab=dc
∴
a、b、c、d四条线段成比例.
(第2小题:,不成比例)
三、比例性质:
等比性质:若,有
(例:)
例3、1、)已知,求的值.
解:设,,
则
2)已知abc≠0,
,求p的值;
例4、已知如图:在△ABC中,AB>AC,点D、E分别在AB、AC上,.
求证:(1);(2).
证明:(1)∵
,∴
(合比性质),
∴
,∴
(2)∵
,∴
,(等比性质),
∴
概念:
一、相似图形:形状相同的图形
概念(1)图形的放大或缩小称为图形的放缩运动.
(2)把形状相同的两个图形称为相似形.
(3)如果两个多边形是相似图形,那么这两个多边形的对应角相等,各对应边的长度成比例(或各对应边长度的比值是相等的)
(三)相似图形的对应关系:
若△ABC与△A’B’C’是相似图形,则对应点是A与A’,B与B’,C与C’;对应边是AB与A’B’,BC与B’C’,AC与A’C’;对应角是∠A与∠A’,∠B与∠B’,∠C与∠C’。
数量关系有:,∠A=∠A’,∠B=∠B’,∠C=∠C’。
如何判断两个多边形相似?
对应角相等,对应边成比例的两个多边形是相似多边形。根据这个定义可以判断两个多边形是否是相似形.
相似多边形的性质:相似多边形对应角相等,对应边的长度成比例
例1梯形ABCD和梯形A1B1C1D1是两个相似的图形(A、B、C、D的对应点分别是A1、B1、C1、D1),且已知,周长之差为28厘米,求ABCD和A1B1C1D1的周长
分析如果两个多边形是相似形,那么对应边的长度成比例,可根据已知条件列出相应的等式。注意“对应”二字
解:设梯形ABCD的周长为x厘米,梯形A1B1C1D1的周长为y厘米
因为梯形ABCD和梯形A1B1C1D1是相似的图形,所以它们的对应边的比值都相等,即
∴
,,,,
∴
,
即,
又∵
解方程组
得
所以梯形ABCD的周长和梯形A1B1C1D1的周长分别为84厘米和56厘米
例2、如图24—1,矩形ABCD中,AB=2AD,线段EF=10.在EF上取一点M,分别以EM、MF为一边作矩形EMNH、矩形MFGN,使矩形MFGN与矩形ABCD相似,且点M与点A、点F与点B、点G与点C、点N与点D分别是对应顶点,令MN=x.求出矩形EMNH的面积S与x的函数关系式
解因为矩形MFGN与矩形ABCD是相似的图形,且点M与
点A、点F与点B、点G与点C、点N与点D分别是对应顶点,
∴
∵AB=2AD,MN=x
∴MF=2NM=2x
∴EM=10-2x
∴
二、比例线段:
【两条线段的比】两条线段长度的比
【比例线段】四条线段a,b,c,d中,如果(a:b=c:d),那么这四条线段a,b,c,d叫做成比例线段,简称比例线段.
线段d是a、b、c的第四比例项.
比例中项:如果作为比例线段的内项是两条相同的线段,即a:b=b:c,或a/b=b/c,那么线段b叫做线段a和c
的比例中项,他们有关系:
☆
比例基本性质:内项积等于外项积.
例3、已知a、b、c、d是四条线段,它们的长度如下,试判断它们是不是成比例线段?
(1)a=1mm,b=0.8cm,c=0.02cm,d=4cm;(2)cm,b=0.4cm,c=40cm,.
解:<统一单位>a=0.1cm,b=0.8cm,c=0.02cm,d=4cm
<最大乘最小,剩下两项乘>
∵dc=4×0.02=0.08,ab=0.1×0.8=0.08
∴
ab=dc
∴
a、b、c、d四条线段成比例.
(第2小题:,不成比例)
三、比例性质:
等比性质:若,有
(例:)
例3、1、)已知,求的值.
解:设,,
则
2)已知abc≠0,
,求p的值;
例4、已知如图:在△ABC中,AB>AC,点D、E分别在AB、AC上,.
求证:(1);(2).
证明:(1)∵
,∴
(合比性质),
∴
,∴
(2)∵
,∴
,(等比性质),
∴
