沪教版(上海)高中数学 高三第一学期第15章15.1 多面体的概念 课件(13张PPT)
文档属性
| 名称 | 沪教版(上海)高中数学 高三第一学期第15章15.1 多面体的概念 课件(13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 272.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 19:35:42 | ||
图片预览





文档简介
15.1 多面体的概念
一、几何体
初中时学习过,平面上由 ?? 构成的图形,统称为平面几何图形。
点和线
现在我们的视野不再局限于平面,而是广阔的空间,空间中由????? 构成的抽象物体统称为几何体。
点、线、面
生活中几何体无处不在
二、多面体
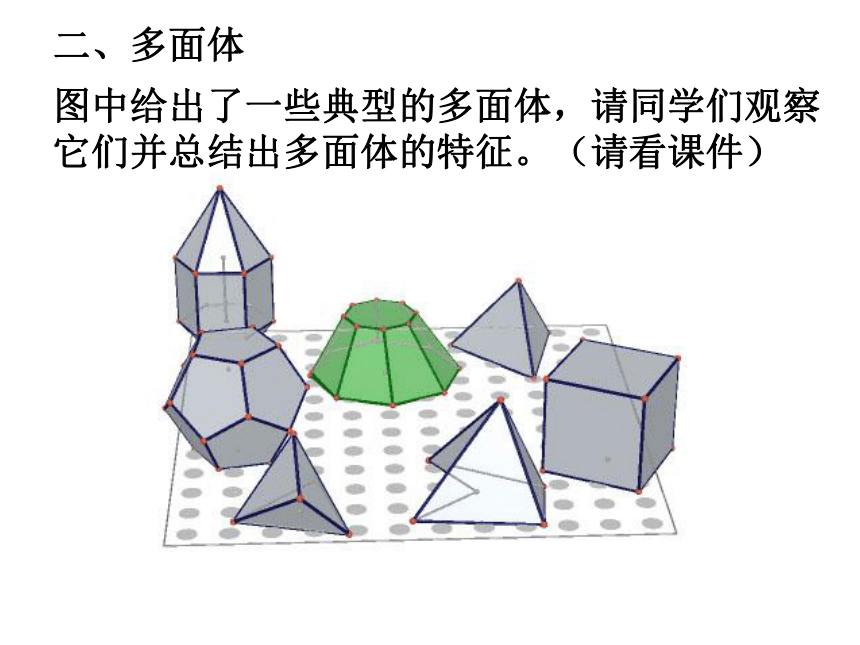
图中给出了一些典型的多面体,请同学们观察它们并总结出多面体的特征。(请看课件)
由 ? ? 围成的 ?? 的几何体,统称为多面体。
封闭,不封闭?
封闭
平面多边形
多面体的面——
构成多面体的各平面多边形
多面体的棱——
多面体各面的交线
多面体的顶点——
多面体的各棱的交点
下面我们看一下生活中一些常见的多面体
这些多面体很常见,它们的共同特点有:
①有没有面平行?
②有没有面全等?
③有没有棱平行?
有两个面互相平行
平行的面上的多边形全等
平行的面之外的棱彼此平行
所以,如果一个多面体有
,且 的棱都互
相平行,那么这个多面体叫做棱柱。
的面互相平行
两个全等的多边形
不在这两个面上
三、棱柱
棱柱中的相关观念: 、 、 、
请看三个棱柱的例子(见几何画板)
辨析:这样的多面体是棱柱么?(见课件)
底面
侧面
侧棱
高
棱柱的底面:两个平行且全等的面
棱柱的侧面:除底面外其他的面,是 ? 形。
棱柱的侧棱:侧面的交线
平行四边
棱柱的高:两底面的距离
提问:课件中的棱柱怎么称呼呢?字母表示?
如图
四、一些特殊棱柱的概念
底面是 平行四边形
平行 六面体
①
侧棱与底面垂直
②
直棱柱
底面是平行四边形
底面是矩形
长方体
③
直棱柱
直平行六面体
正棱柱
如图
底面是正多边形
各棱都相等
正方体
图中分别是直三棱柱、直四棱柱、直五棱柱
图中分别是正几棱柱?
例1、设M={正四棱柱},N={长方体},Q={正方体}, P={直四棱柱},R={四棱柱}, 请写出它们的包含关系
答:Q ? M ? N ? P ? R
五、棱锥
观察这些棱锥并总结棱锥的特征。(请看课件)
所以,如果一个多面体有一个面是
且 的棱都 ,那么这个多
面体叫做棱锥。
特征1:
有一个面是多边形
特征2:
不在这个面上的棱共点
多边形,
不在这个面上
共点
提问:课件中的棱锥怎么称呼呢?用字母如何表示?
棱锥中的相关观念: 、 、 、
再看三个棱锥的例子(见几何画板)
底面
侧面
侧棱
顶点、
棱锥的底面:那个多边形的面
棱锥的侧面:除底面外其他的面。
棱锥的侧棱:侧面的交线
棱锥的顶点:所有侧棱的交点
棱锥的高:顶点到底面的距离
高
六、特殊的棱锥——正棱锥
观察几个正棱锥的例子,探讨正棱锥的特征。
①底面:
是一个正多边形
②顶点与底面的关系:
在底面的射影是底面的中心
所以,底面是 ?? 且顶点在底面的射影
?? 的棱锥叫做正棱锥。
正多边形
是这个正多边形的中心
练习:看图说话
七、小结
棱柱
棱锥
几何体
多面体
八、作业:《堂堂练》P15-P16/1~8
正棱锥
一、几何体
初中时学习过,平面上由 ?? 构成的图形,统称为平面几何图形。
点和线
现在我们的视野不再局限于平面,而是广阔的空间,空间中由????? 构成的抽象物体统称为几何体。
点、线、面
生活中几何体无处不在
二、多面体
图中给出了一些典型的多面体,请同学们观察它们并总结出多面体的特征。(请看课件)
由 ? ? 围成的 ?? 的几何体,统称为多面体。
封闭,不封闭?
封闭
平面多边形
多面体的面——
构成多面体的各平面多边形
多面体的棱——
多面体各面的交线
多面体的顶点——
多面体的各棱的交点
下面我们看一下生活中一些常见的多面体
这些多面体很常见,它们的共同特点有:
①有没有面平行?
②有没有面全等?
③有没有棱平行?
有两个面互相平行
平行的面上的多边形全等
平行的面之外的棱彼此平行
所以,如果一个多面体有
,且 的棱都互
相平行,那么这个多面体叫做棱柱。
的面互相平行
两个全等的多边形
不在这两个面上
三、棱柱
棱柱中的相关观念: 、 、 、
请看三个棱柱的例子(见几何画板)
辨析:这样的多面体是棱柱么?(见课件)
底面
侧面
侧棱
高
棱柱的底面:两个平行且全等的面
棱柱的侧面:除底面外其他的面,是 ? 形。
棱柱的侧棱:侧面的交线
平行四边
棱柱的高:两底面的距离
提问:课件中的棱柱怎么称呼呢?字母表示?
如图
四、一些特殊棱柱的概念
底面是 平行四边形
平行 六面体
①
侧棱与底面垂直
②
直棱柱
底面是平行四边形
底面是矩形
长方体
③
直棱柱
直平行六面体
正棱柱
如图
底面是正多边形
各棱都相等
正方体
图中分别是直三棱柱、直四棱柱、直五棱柱
图中分别是正几棱柱?
例1、设M={正四棱柱},N={长方体},Q={正方体}, P={直四棱柱},R={四棱柱}, 请写出它们的包含关系
答:Q ? M ? N ? P ? R
五、棱锥
观察这些棱锥并总结棱锥的特征。(请看课件)
所以,如果一个多面体有一个面是
且 的棱都 ,那么这个多
面体叫做棱锥。
特征1:
有一个面是多边形
特征2:
不在这个面上的棱共点
多边形,
不在这个面上
共点
提问:课件中的棱锥怎么称呼呢?用字母如何表示?
棱锥中的相关观念: 、 、 、
再看三个棱锥的例子(见几何画板)
底面
侧面
侧棱
顶点、
棱锥的底面:那个多边形的面
棱锥的侧面:除底面外其他的面。
棱锥的侧棱:侧面的交线
棱锥的顶点:所有侧棱的交点
棱锥的高:顶点到底面的距离
高
六、特殊的棱锥——正棱锥
观察几个正棱锥的例子,探讨正棱锥的特征。
①底面:
是一个正多边形
②顶点与底面的关系:
在底面的射影是底面的中心
所以,底面是 ?? 且顶点在底面的射影
?? 的棱锥叫做正棱锥。
正多边形
是这个正多边形的中心
练习:看图说话
七、小结
棱柱
棱锥
几何体
多面体
八、作业:《堂堂练》P15-P16/1~8
正棱锥
