高中数学人教A版(2019)必修第一册第五章5.1.2弧度制 课件(21张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修第一册第五章5.1.2弧度制 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 358.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:04:42 | ||
图片预览





文档简介
5.1.2 弧度制
第五章 三角函数
1. 在平面几何里,度量角的大小用什么单位?
规定:圆周1/360的圆心角称作1°角。
角度制的单位有:度、分、秒。
复习
2.1°的角是如何定义的?
这种用度做单位来度量角的制度叫做角度制 .
在数学和其他科学研究中还经常用到另一种度量角的制度 — 弧度制,它是如何定义呢?
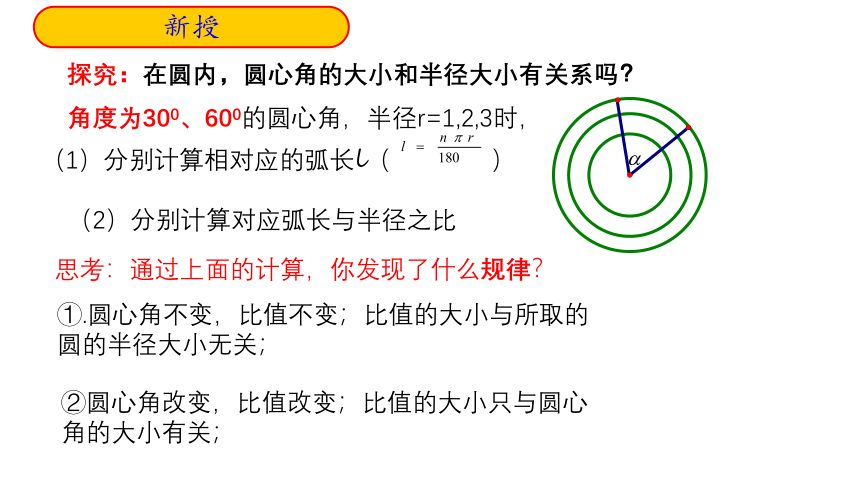
(2)分别计算对应弧长与半径之比
探究:在圆内,圆心角的大小和半径大小有关系吗?
思考:通过上面的计算,你发现了什么规律?
①.圆心角不变,比值不变;比值的大小与所取的圆的半径大小无关;
②圆心角改变,比值改变;比值的大小只与圆心角的大小有关;
(1)分别计算相对应的弧长l( )
角度为300、600的圆心角,半径r=1,2,3时,
新授
把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角.
1.弧度的概念
约定: 正角的弧度数为正数,
负角的弧度数为负数,
零角的弧度数为0.
r
l=r
O
A
B
弧度制:这种以弧度作为单位来度量角的单位制叫做弧度制,它的单位是弧度,单位符号是rad.
1rad
2rad
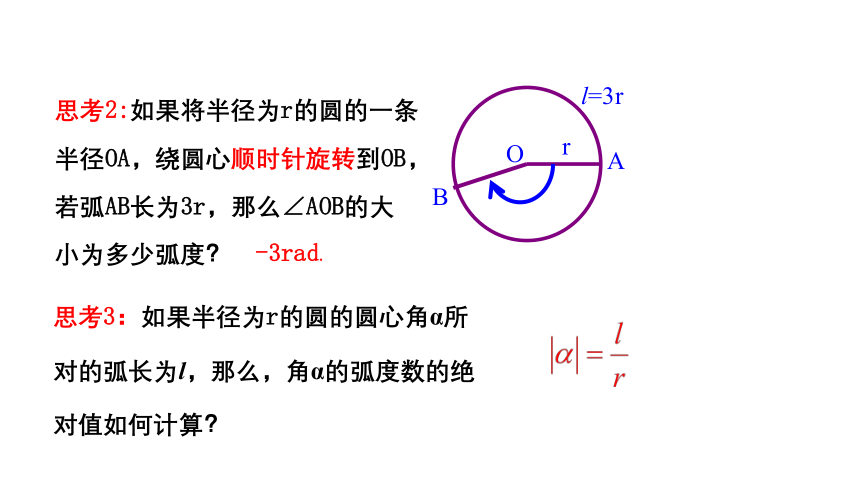
思考1:圆的半径为r,弧长分别为r,2r,则它们所对圆心角的弧度数是多少?
-3rad.
思考3:如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值如何计算?
l=3r
O
A
B
r
思考2:如果将半径为r的圆的一条
半径OA,绕圆心顺时针旋转到OB,
若弧AB长为3r,那么∠AOB的大
小为多少弧度?
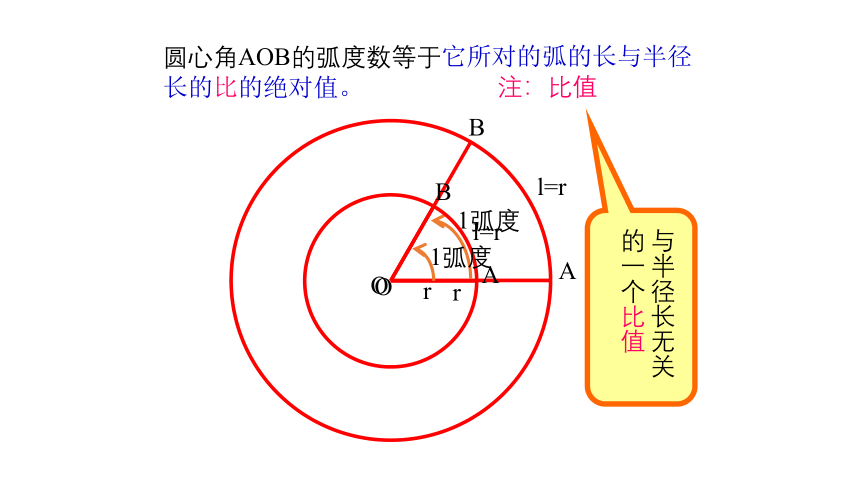
圆心角AOB的弧度数等于它所对的弧的长与半径
长的比的绝对值。
1弧度
r
l=r
O
A
B
1弧度
r
l=r
O
A
B
与半径长无关
的一个比值
注:比值
2.角度与弧度的换算
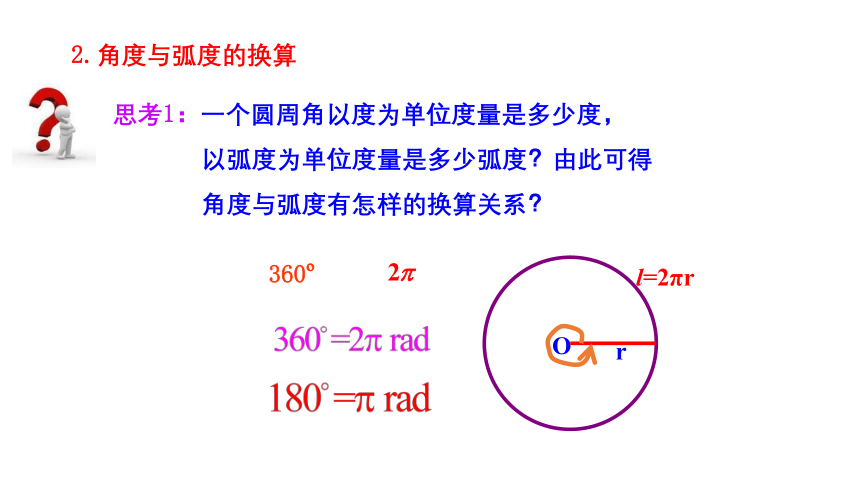
思考1:一个圆周角以度为单位度量是多少度,
以弧度为单位度量是多少弧度?由此可得
角度与弧度有怎样的换算关系?
l=2πr
O
r
360?
思考2:根据上述关系,1°等于多少弧度,
1 rad等于多少度?
例1.把 67°30′化成弧度:
注:角度制与弧度制互化时要抓住 180°= ? rad 这个关键。
解 (1)
(2)
注: 常规写法
① 用弧度数表示角时,常常把弧度数
写成多少?的形式,不必写成小数.
③弧度与角度不能混用.即不能出现这样的形式:
②用弧度制表示角时,”弧度”二字或 ”rad”通常略去不写,面只写该角所对应的弧度数.
总结:根据度与弧度的换算关系,填写下表中特殊角的度数或弧度数.
角度
?
?
?
?
?
弧度
?
?
?
?
?
?
弧度制下角的集合与实数集的一一对应:
正角
零角
负角
正实数
零
负实数
任意角的集合
实数集R
注:扇形的面积公式中的角都用弧度数,不能用度数
达标检测
1.什么叫1弧度角?
2.“角度制”与“弧度制”的联系与区别.
3.弧长公式与扇形面积公式.
课堂小结
第五章 三角函数
1. 在平面几何里,度量角的大小用什么单位?
规定:圆周1/360的圆心角称作1°角。
角度制的单位有:度、分、秒。
复习
2.1°的角是如何定义的?
这种用度做单位来度量角的制度叫做角度制 .
在数学和其他科学研究中还经常用到另一种度量角的制度 — 弧度制,它是如何定义呢?
(2)分别计算对应弧长与半径之比
探究:在圆内,圆心角的大小和半径大小有关系吗?
思考:通过上面的计算,你发现了什么规律?
①.圆心角不变,比值不变;比值的大小与所取的圆的半径大小无关;
②圆心角改变,比值改变;比值的大小只与圆心角的大小有关;
(1)分别计算相对应的弧长l( )
角度为300、600的圆心角,半径r=1,2,3时,
新授
把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角.
1.弧度的概念
约定: 正角的弧度数为正数,
负角的弧度数为负数,
零角的弧度数为0.
r
l=r
O
A
B
弧度制:这种以弧度作为单位来度量角的单位制叫做弧度制,它的单位是弧度,单位符号是rad.
1rad
2rad
思考1:圆的半径为r,弧长分别为r,2r,则它们所对圆心角的弧度数是多少?
-3rad.
思考3:如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值如何计算?
l=3r
O
A
B
r
思考2:如果将半径为r的圆的一条
半径OA,绕圆心顺时针旋转到OB,
若弧AB长为3r,那么∠AOB的大
小为多少弧度?
圆心角AOB的弧度数等于它所对的弧的长与半径
长的比的绝对值。
1弧度
r
l=r
O
A
B
1弧度
r
l=r
O
A
B
与半径长无关
的一个比值
注:比值
2.角度与弧度的换算
思考1:一个圆周角以度为单位度量是多少度,
以弧度为单位度量是多少弧度?由此可得
角度与弧度有怎样的换算关系?
l=2πr
O
r
360?
思考2:根据上述关系,1°等于多少弧度,
1 rad等于多少度?
例1.把 67°30′化成弧度:
注:角度制与弧度制互化时要抓住 180°= ? rad 这个关键。
解 (1)
(2)
注: 常规写法
① 用弧度数表示角时,常常把弧度数
写成多少?的形式,不必写成小数.
③弧度与角度不能混用.即不能出现这样的形式:
②用弧度制表示角时,”弧度”二字或 ”rad”通常略去不写,面只写该角所对应的弧度数.
总结:根据度与弧度的换算关系,填写下表中特殊角的度数或弧度数.
角度
?
?
?
?
?
弧度
?
?
?
?
?
?
弧度制下角的集合与实数集的一一对应:
正角
零角
负角
正实数
零
负实数
任意角的集合
实数集R
注:扇形的面积公式中的角都用弧度数,不能用度数
达标检测
1.什么叫1弧度角?
2.“角度制”与“弧度制”的联系与区别.
3.弧长公式与扇形面积公式.
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
