高中数学人教A版(2019)选择性必修第二册第四章 数列 4.3.1 等比数列的概念及 通项公式课件(21张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修第二册第四章 数列 4.3.1 等比数列的概念及 通项公式课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:07:50 | ||
图片预览







文档简介
第四章 数列
4.3.1 等比数列的概念及
通项公式
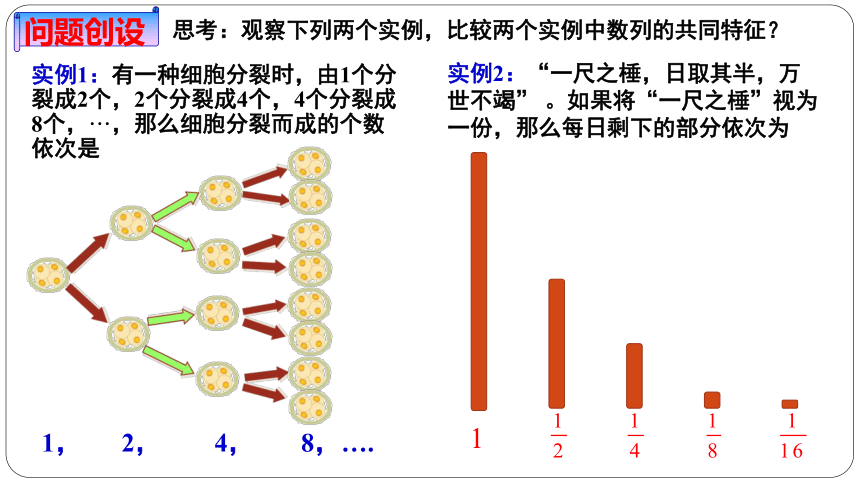
思考:观察下列两个实例,比较两个实例中数列的共同特征?
1, 2, 4, 8,….
问题创设
实例1:有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个,···,那么细胞分裂而成的个数依次是
实例2:“一尺之棰,日取其半,万世不竭” 。如果将“一尺之棰”视为一份,那么每日剩下的部分依次为
数列①从第2项起,每一项与它前一项的比都等于____
数列②从第2项起,每一项与它前一项的比都等于____
2
特点:从第二项起,每一项与它的前一项的比是同一常数(等比)
1,2,4,8,….
问题创设
你能通过运算发现数列的取值规律吗?
思考:用数学符号语言(递推公式)怎样表示等比数列的定义呢?
一般地,如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列。这个常数就叫做等比数列的公比, 公比通常用字母 q 表示。
1、等比数列的定义:
或
注意事项:1、等比数列的每一项都不为0,即an≠0。
2、公比q≠0
知识讲解
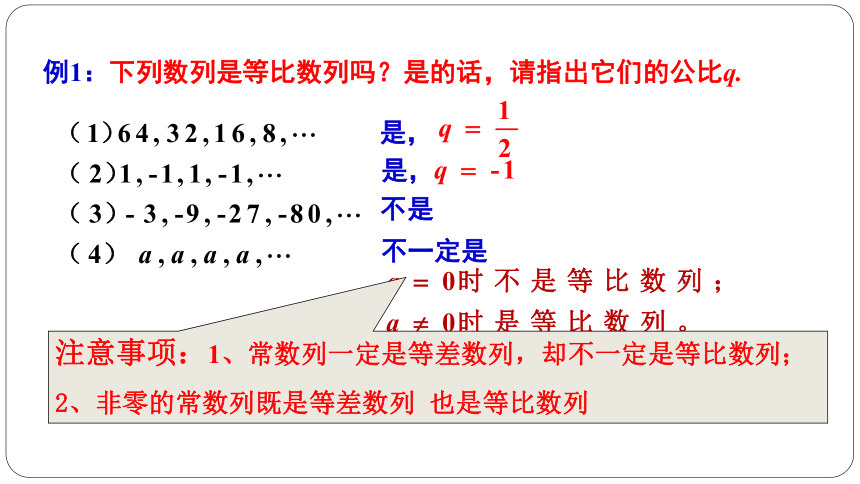
例1:下列数列是等比数列吗?是的话,请指出它们的公比q.
不是
不一定是
是,
是,
注意事项:1、常数列一定是等差数列,却不一定是等比数列;
2、非零的常数列既是等差数列 也是等比数列
知识讲解
2、等比数列的通项公式:
方法2:
由定义得:
若将上述n-1个等式相乘,便可得:
即
“累乘法”
?
?
?
例2、
?
?
如果在a与b中间插入一个数G,使a,G,b组成一个等比数列,则中间的数G叫做a与b的等比中项,且
注意:
(1)若实数a、b有等比中项,则a、b符号相同;
(2)若实数a、b有等比中项,则该等比中项必有两个值
若G2=ab,则a,G,b一定成等比数列吗?
3、等比中项:
知识讲解
?
?
?
?
-4
?
练习2、能否在下列两个数中间插入一个数,使这三个数组成一个等比数列?可以的话,请求出插入的数字
?
练习3、
?
?
?
1.定义
2.公比(差)
3.等比(差)
中项
4.通项公式
q≠0
d∈R
等比中项
等差中项
等差数列
等比数列
四、课时小结
当堂检测
?
?
?
?
当堂检测
当堂检测
当堂检测
当堂检测
4.3.1 等比数列的概念及
通项公式
思考:观察下列两个实例,比较两个实例中数列的共同特征?
1, 2, 4, 8,….
问题创设
实例1:有一种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个,···,那么细胞分裂而成的个数依次是
实例2:“一尺之棰,日取其半,万世不竭” 。如果将“一尺之棰”视为一份,那么每日剩下的部分依次为
数列①从第2项起,每一项与它前一项的比都等于____
数列②从第2项起,每一项与它前一项的比都等于____
2
特点:从第二项起,每一项与它的前一项的比是同一常数(等比)
1,2,4,8,….
问题创设
你能通过运算发现数列的取值规律吗?
思考:用数学符号语言(递推公式)怎样表示等比数列的定义呢?
一般地,如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列。这个常数就叫做等比数列的公比, 公比通常用字母 q 表示。
1、等比数列的定义:
或
注意事项:1、等比数列的每一项都不为0,即an≠0。
2、公比q≠0
知识讲解
例1:下列数列是等比数列吗?是的话,请指出它们的公比q.
不是
不一定是
是,
是,
注意事项:1、常数列一定是等差数列,却不一定是等比数列;
2、非零的常数列既是等差数列 也是等比数列
知识讲解
2、等比数列的通项公式:
方法2:
由定义得:
若将上述n-1个等式相乘,便可得:
即
“累乘法”
?
?
?
例2、
?
?
如果在a与b中间插入一个数G,使a,G,b组成一个等比数列,则中间的数G叫做a与b的等比中项,且
注意:
(1)若实数a、b有等比中项,则a、b符号相同;
(2)若实数a、b有等比中项,则该等比中项必有两个值
若G2=ab,则a,G,b一定成等比数列吗?
3、等比中项:
知识讲解
?
?
?
?
-4
?
练习2、能否在下列两个数中间插入一个数,使这三个数组成一个等比数列?可以的话,请求出插入的数字
?
练习3、
?
?
?
1.定义
2.公比(差)
3.等比(差)
中项
4.通项公式
q≠0
d∈R
等比中项
等差中项
等差数列
等比数列
四、课时小结
当堂检测
?
?
?
?
当堂检测
当堂检测
当堂检测
当堂检测
