高中数学人教A版必修1第三章3.1.1 方程的根与函数的零点课件(20张PPT)
文档属性
| 名称 | 高中数学人教A版必修1第三章3.1.1 方程的根与函数的零点课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 823.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-23 21:45:31 | ||
图片预览








文档简介
方程
函数
函
数
的
图
象
方程的实数根
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
y
x
0
-1
2
1
1
2
问题1 求出表中一元二次方程的实数根,画出相应的二次函数图像的简图,并写出函数的图象与x轴的交点坐标.
问题·探究
-1, 3
1
方程
的根
函数
的图象
判别式
△ =
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
问题2 若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍然成立?
问题·探究
归纳:
如果一元二次方程没有实数根,相应二次函数图像与x轴就没有交点;
如果一元二次方程有实数根,它的实数根就是相应二次函数的图像与x轴交点的横坐标。
一、函数零点的定义:
对于函数 ,我们把使 的实数 叫做函数 的零点.
零点不是点,零点指的是一个实数;
而且函数f(x)的零点即为f(x)=0的实根;
也就是函数图像与x轴交点的横坐标.
注意:
零点是一个点吗?
课堂练习:函数
的零点是: ( )
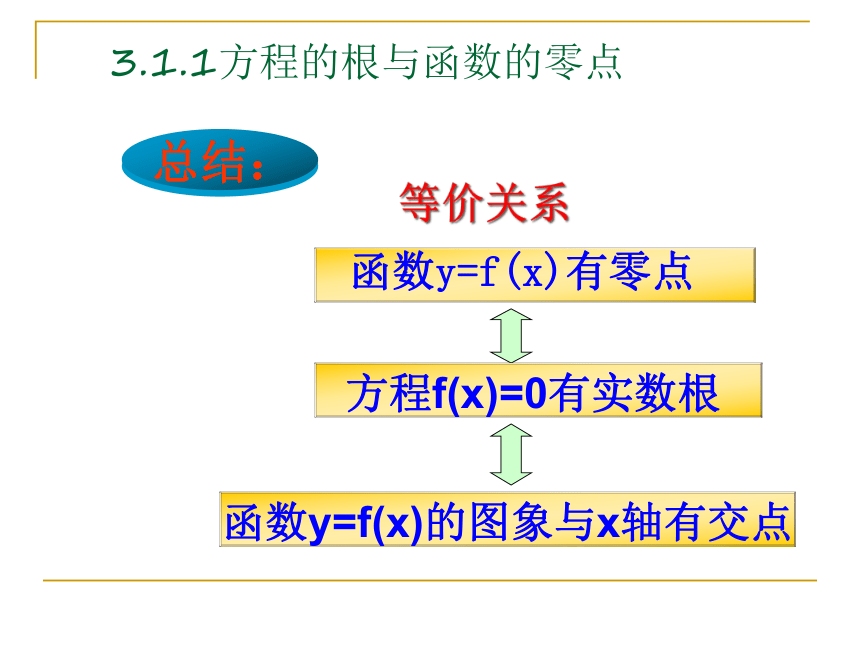
函数y=f(x)的图象与x轴有交点
总结:
等价关系
方程f(x)=0有实数根
函数y=f(x)有零点
3.1.1方程的根与函数的零点
Ⅰ
Ⅱ
思考1:下列哪组图可以确定小马一定过了河?
三、零点的存在性定理
思考2:
将河流抽象成x轴,将前后的两个位置视为A、B两点。
请问当A、B与x轴怎样的位置关系时,AB间的一段连续不
断的函数图象与x轴一定会有交点?
x
思考3:A、B与x轴的位置关系,如何用数学符号(式
子)来表示?
a
b
O
y
问题·探究
0
1
2
3
4
5
-1
-2
1
2
3
4
5
-1
-2
-3
-4
x
y
结论理解
思考1:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,函数y=f(x)在区间(a,b)内有零点吗?
结论理解
思考2;若只给条件f(a) · f(b)<0能否保证在(a,b)有零点?
结论理解
思考3:有零点是指有几个零点呢?只有一个吗?
思考4:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,那么当f(a)·f(b)>0时,函数y=f(x)在区间(a,b)内一定没有零点吗?
思考5:若在区间(a,b)有零点时,一定有f(a)·f(b) <0吗?
例1、已知函数f(x)的图像是连续不断的,且有如下对应值表:
X
1
2
3
4
5
6
f(x)
23
9
-7
11
-5
-12
问:那么函数在区间[1 , 6]上的零点至少有几个,哪些区间上一定存在零点
答案:至少有3个零点
分别在区间 (2, 3),(3,4),(4,5)上
1.函数y=f(x)是定义在区间[a,b]上的增函数,且f(a)f(b)<0,则函数y=f(x)在区间(a,b)内( )
A.至少有一个零点
B.至多有一个零点
C.只有一个零点
D.有两个零点
课堂练习
2.函数y=f(x)在区间[a,b]上的图象是连续不断的曲线,且f(a)f(b)<0,则函数y=f(x)在区间(a,b)内( )
A.至少有一个零点
B.至多有一个零点
C.只有一个零点
D.有两个零点
课堂练习
3.函数y=f(x),若f(-1)f(3)<0,则下列判断正确的是( )
A.方程f(x)=0一定有根
B.方程f(x)=0一定无根
C.方程f(x)=0一定有两根
D.方程f(x)=0可能无根
课堂练习
反思小结:
1.函数零点的定义
2.等价关系
3.零点存在定理
数学思想方法 :数形结合
化归与转化
布置作业
函数
函
数
的
图
象
方程的实数根
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
.
.
x
y
0
-1
3
2
1
1
2
5
4
3
.
y
x
0
-1
2
1
1
2
问题1 求出表中一元二次方程的实数根,画出相应的二次函数图像的简图,并写出函数的图象与x轴的交点坐标.
问题·探究
-1, 3
1
方程
的根
函数
的图象
判别式
△ =
△>0
△=0
△<0
函数的图象
与 x 轴的交点
有两个相等的
实数根x1 = x2
没有实数根
x
y
x1
x2
0
x
y
0
x1
x
y
0
(x1,0) , (x2,0)
(x1,0)
没有交点
两个不相等
的实数根x1 、x2
问题2 若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍然成立?
问题·探究
归纳:
如果一元二次方程没有实数根,相应二次函数图像与x轴就没有交点;
如果一元二次方程有实数根,它的实数根就是相应二次函数的图像与x轴交点的横坐标。
一、函数零点的定义:
对于函数 ,我们把使 的实数 叫做函数 的零点.
零点不是点,零点指的是一个实数;
而且函数f(x)的零点即为f(x)=0的实根;
也就是函数图像与x轴交点的横坐标.
注意:
零点是一个点吗?
课堂练习:函数
的零点是: ( )
函数y=f(x)的图象与x轴有交点
总结:
等价关系
方程f(x)=0有实数根
函数y=f(x)有零点
3.1.1方程的根与函数的零点
Ⅰ
Ⅱ
思考1:下列哪组图可以确定小马一定过了河?
三、零点的存在性定理
思考2:
将河流抽象成x轴,将前后的两个位置视为A、B两点。
请问当A、B与x轴怎样的位置关系时,AB间的一段连续不
断的函数图象与x轴一定会有交点?
x
思考3:A、B与x轴的位置关系,如何用数学符号(式
子)来表示?
a
b
O
y
问题·探究
0
1
2
3
4
5
-1
-2
1
2
3
4
5
-1
-2
-3
-4
x
y
结论理解
思考1:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,函数y=f(x)在区间(a,b)内有零点吗?
结论理解
思考2;若只给条件f(a) · f(b)<0能否保证在(a,b)有零点?
结论理解
思考3:有零点是指有几个零点呢?只有一个吗?
思考4:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,那么当f(a)·f(b)>0时,函数y=f(x)在区间(a,b)内一定没有零点吗?
思考5:若在区间(a,b)有零点时,一定有f(a)·f(b) <0吗?
例1、已知函数f(x)的图像是连续不断的,且有如下对应值表:
X
1
2
3
4
5
6
f(x)
23
9
-7
11
-5
-12
问:那么函数在区间[1 , 6]上的零点至少有几个,哪些区间上一定存在零点
答案:至少有3个零点
分别在区间 (2, 3),(3,4),(4,5)上
1.函数y=f(x)是定义在区间[a,b]上的增函数,且f(a)f(b)<0,则函数y=f(x)在区间(a,b)内( )
A.至少有一个零点
B.至多有一个零点
C.只有一个零点
D.有两个零点
课堂练习
2.函数y=f(x)在区间[a,b]上的图象是连续不断的曲线,且f(a)f(b)<0,则函数y=f(x)在区间(a,b)内( )
A.至少有一个零点
B.至多有一个零点
C.只有一个零点
D.有两个零点
课堂练习
3.函数y=f(x),若f(-1)f(3)<0,则下列判断正确的是( )
A.方程f(x)=0一定有根
B.方程f(x)=0一定无根
C.方程f(x)=0一定有两根
D.方程f(x)=0可能无根
课堂练习
反思小结:
1.函数零点的定义
2.等价关系
3.零点存在定理
数学思想方法 :数形结合
化归与转化
布置作业
